卷积积分的快速分段和定限方法

海 涛

(安徽工程大学 电气工程学院，安徽 芜湖 241000)



卷积积分的快速分段和定限方法

海 涛

(安徽工程大学 电气工程学院，安徽 芜湖 241000)

卷积积分在积分变换、控制理论、信号与系统以及电路分析等学科中应用广泛，是一个重要的数学工具．虽然卷积积分的计算方法较多，但要准确计算出卷积积分并非易事，正确地分段和定限是计算卷积积分的两大难点．从卷积积分的定义出发，经严密的数学推导获得一种卷积积分的快速分段和定限方法．在此基础上，进一步绘制出卷积积分的快速分段和定限图，使得卷积积分的分段和定限更加直观易行．实例表明，应用快速分段和定限法能够快速准确地求解卷积积分．

卷积积分；解析法；分段；定限

随着计算机技术的飞速发展以及信号与系统理论研究的深入，卷积方法的应用日益广泛[1]．卷积方法包括卷积积分和卷积和，研究仅讨论卷积积分．卷积积分的计算方法论述较多[1-7]，这些计算方法可以归纳为解析法、图解法、利用卷积积分的性质法及变换域法．目前，利用卷积积分的性质法和变换域法两种方法的研究比较充分，而解析法和图解法两种方法在确定积分限的问题上讨论不够全面[3]．目前，积分限的确定主要借助于图解法[1-3,7]，虽然用图解法确定积分限稍微简单一些，但其计算过程繁琐且易出错[7]．鉴于此，从卷积积分的定义式出发，应用数学分析方法推导出一种简单易懂的卷积积分分段和定限方法，并绘制卷积积分分段和定限图，使得计算更加快速准确．

1 卷积积分的定义

卷积积分源于连续时间信号的分解，它利用系统的单位冲激响应求解系统对任意输入信号的零状态响应．假设系统的输入信号和系统的单位冲激响应分别为f(t)和h(t)，则系统的零状态响应y(t)可以定义为：

(1)

此积分被称为卷积积分，卷积积分中含τ和t两个变量．在积分的计算过程中，τ是积分变量，t是参变量；卷积积分后的结果为t的函数．

2 卷积积分的分段和定限

为了获得卷积积分的分段时限和每段的积分限，假设f(t)的定义域为t∈[t11,t12]，h(t)的定义域为t∈[t21,t22]，则由式(1)可知：

(2)

(3)

由式(2)、式(3)可得y(t)的定义域为：

(4)

由式(4)可得：

结论1 f(t)和h(t)卷积结果y(t)的定义域上、下限分别是两个被积函数f(t)和h(t)的定义域上、下限之和．

这里仅获得了y(t)的定义域，即y(t)的非零区间．为了获得y(t)的时域分段，下面将对式(2)、式(3)和式(4)做进一步处理．

由式(3)可得:

(5)

由式(2)、式(5)可得:

(6)

其中，

(7)

(8)

由式(7)可将式(4)改写为:

(9)

由式(8)可将式(4)改写为:

(10)

由式(9)、式(10)可得:

t∈[t11+t21,min(t11+t22,t12+t21)]∪(min(t11+t22,t12+t22),max(t11+t22,t12+t21))∪[max(t11+t22,t12+t21),t12+t22],

(11)

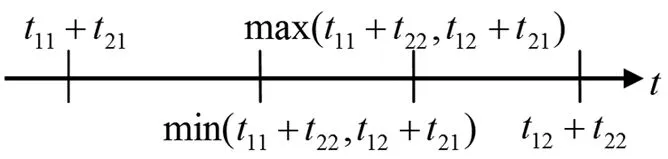
图1 卷积积分快速分段图

式(11)实际上把y(t)的定义域分成了3段，可以表示成图1的形式，卷积积分快速分段图如图1所示．由图1可得y(t)的定义域的分段结论(结论2)．

结论2 两个被积函数f(t)和h(t)的定义域上、下限交叉分别相加，将获得的两个和以及y(t)的定义域上限和下限按大小顺序排列在时间轴上，从而获得卷积结果y(t)的分段时限．

由图1可知，若t22=t12=∞,则min(t11+t22，t12+t21)=max(t11+t22,t12+t21)=∞，t12+t22=∞，此时图1退化为两段(-∞,t11+t21)∪[t11+t21,∞);若t11+t22=t12+t21,(min(t11+t22，t12+t21),max(t11+t22,t12+t21))=Φ,则该段消失．

在获得y(t)的定义域分段结果的基础上，利用式(4)、式(7)和式(8)可以快速确定每段卷积积分的上下限，如图2所示．由图2可知，只要已知f(t)和h(t)的定义域，卷积积分快速分段与定限就可轻而易举地获得．这样，利用解析法求解卷积积分的两大难点就迎刃而解了．

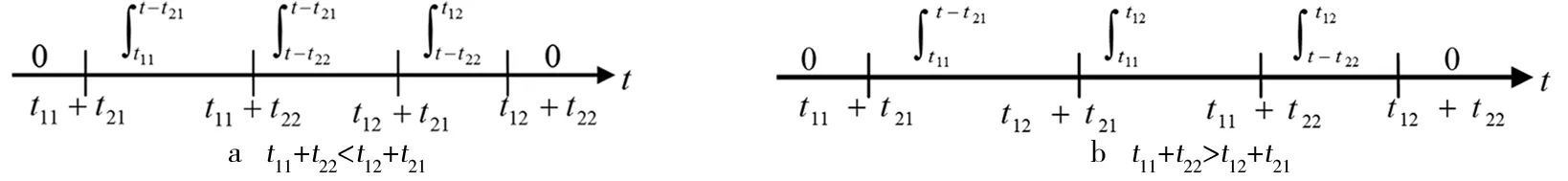
图2 卷积积分快速分段与定限图

3 应用实例

利用卷积积分快速分段与定限图可以快速准确地确定卷积结果的分段时限和每段的积分上下限，从而简化卷积积分的计算．

图3 例1的被积函数

例1 已知两个时限函数f(t)和h(t)如图3所示，求y(t)=f(t)*h(t)．

解：由图3可知，t11=4，t12=5，t21=1，t22=3.由于t11+t22>t12+t21，根据图2b画出卷积积分快速分段定限图如图4所示．

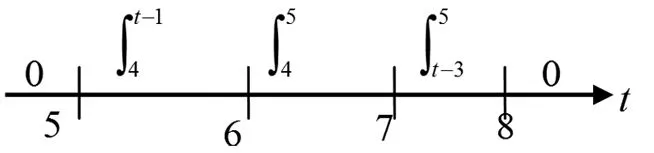
图4 例1的快速分段定限图

由图4和式(1)可得

例2 已知f(t)=u(t)，h(t)=e-tu(t),求y(t)=f(t)*h(t)．

解：依题意知，t11=0，t12=∞，t21=0，t22=∞.因t11+t21=0,t12+t21=t11+t22=t12+t22=∞，图2a或图2b退化为两段(-∞,t11+t21)∪[t11+t21，∞)；因此，例2的卷积积分快速分段定限图如图5所示．

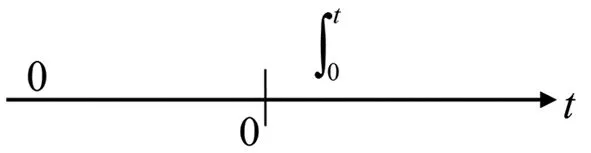
图5 例2的快速分段定限图

由图5和式(1)可得

由以上两例可以看出，卷积积分快速分段与定限图极大地简化了卷积积分的计算过程．

4 结论

针对卷积积分分段和定限的两个计算难点，从卷积积分的定义出发，经严格的数学推导，获得了卷积积分分段和定限的快速方法，实例表明该方法简单易行．

[1] 郑君里,应启珩,杨为理.信号与系统：第三版[M].北京:高等教育出版社,2011.

[2] 温卫,任克强.卷积积分与卷积和解法分析[J].江西理工大学学报，2006，27(1):27-29.

[3] 黄裕建.卷积积分上下限的确定与计算方法[J].河南教育学院学报：自然科学版,2006,15(4):14-16.

[4] 王晓平.卷积积分的基本计算方法[J].常州工学院学报，2002，16(4):54-57.

[5] 张爱清,叶新荣.卷积积分的计算方法探讨[J].科技信息，2013(11):51-52.

[6] 杨永生,赵梅.从时域和频域两种角度探讨卷积积分[J].科技信息，2010(11):165-168.

[7] 唐建锋,杨辉,罗湘南.信号与系统中卷积计算方法探讨[J].科技信息，2012(4):16.

A Fast Segmentation and Definite Bounds Method of Convolution Integral

HAI Tao

(College of Electrical Engineering，Anhui Polytechnic University,Wuhu 241000,China)

Convolution integral is an important mathematical tool widely used in many subjects such as integral transform, control theory,signal and system,and the circuit analysis.Although there are many convolution integral calculation methods,it is still hard to accurately calculate convolution integral.Two difficulties lies in:how to correctly determine the time segmentations of the convolution results and the integral upper and lower bounds in each segmentation called for short segmentation and definite bounds.Starting from the definition of convolution integral,a convolution integral fast segmentation and definite bounds method is proposed by strict mathematical deduction.On this basis,a convolution integral of fast segmentation and definite bounds figure is drawn,which makes the segmentation and definite bounds more intuitive and easy.Some examples show that the fast segmentation and definite bounds method can rapidly and accurately solve the convolution integral.

convolution integral;analytic method;segmentation;definite bounds

1672-2477(2016)05-0085-03

安徽工程大学教研基金资助项目(2015ZYZHGG02，2015JCJXZZ03)

海 涛(1975-)，男，安徽芜湖人，副教授，博士．

0172;TN91

A