对“区间”概念的认识与思考
2016-12-17邓冬华
邓冬华
(四川省成都市第二十中学,610036)
对“区间”概念的认识与思考
邓冬华
(四川省成都市第二十中学,610036)
“区间”概念是高中数学的基础概念,但在笔者第二轮执教高一的过程中对此产生了诸多疑惑.通过对学生常见错误及惯用写法的深入探究,豁然开朗,现整理成文,敬请指正.
一、背景:单调区间能否用“∪”连接
到底是命题“单调区间不能用‘∪’连接”本身是错误的,还是我们对“单调区间不能用‘∪’连接”的理解有误呢?导致这一问题的根本原因是什么?要解决这些问题,应先回到基本的定义.
二、研读:再读“区间”定义
人教A版高中数学必修1中对“区间”给出了如下的定义:
设a,b是两个实数,而且a (1)满足不等式a≤x≤b的实数x的集合叫做闭区间,表示为[a,b]; (2)满足不等式a (3)满足不等式a≤x 这里的实数a与实数b都叫做相应区间的端点.实数集R,x≥a,x>a,x≤a,x 1.区间端点的实数表示 在区间的定义中,规定a,b∈R,所以区间表示且仅能表示实数集.故不能出现(30°,60°)、(-90°+2kπ,90°+2kπ)(k∈Z)等不规范的区间.在现实的教学中,像(-90°+2kπ,90°+2kπ)(k∈Z)这样的区间在学生中经常出现,而笔者以前给学生的解释是不能将角度制与弧度制混用,现在看来这种解释未能触及问题的本质. 2.区间与集合的关系 由区间的定义可知,集合{x|a (1)在a (2)集合{x|a ③ 集合{x|a 上面定理谈到区间必是一个连通集,即区间是连续的数集,这对我们认识区间概念有直接的帮助. 3.对“单调区间不能用‘∪’连接”的理解 首先回顾单调区间的定义:函数f(x)在定义域的某个区间D上是增函数或减函数,则区间D叫做y=f(x)的单调区间,由此可见,单调区间必是区间. 因此,函数“单调区间能否用‘∪’连接”不能一概而论.若函数的单调区间连续,最后结果应当用“∪”连接,并化简;若单调区间不连续,则不能用“∪”连接. 4.定义域与参数取值范围结果的呈现 先看下面的问题:函数f(x)=lg sin x的定义域是______.由sin x>0可得2kπ 那么,多个独立区间的“∪”能作为定义域吗?比如,函数f(x)的定义域可以是(-∞,4)∪(4,+∞)吗?更一般地,多个区间的“∪”可以作为最终的结果呈现吗?比如,实数a的取值范围可以是(1,3)∪(4,10)吗?不幸的是,这种常见写法的正确性是有争议的.认为这种写法错误的理由是:(1,3)∪(4,10)是两个集合在进行集合的并集运算,不是最简结果,应写成集合{x|1 函数r=f(p)的图象如图1所示. (1)函数r=f(p)的定义域是什么? (2)函数r=f(p)的值域是什么? (3)r取何值时,只有唯一的p值与之对应? 注意,《必修1教师教学用书》给出的参考答案是“(1){p|-5≤p≤0或2≤p<6};(3)r在{r|0≤r<2或r>5}上取值时”,而不是“(1)[-5,0]∪[2,6);(3)[-5,2)∪(5,+∞)”. 事实上,造成这种争议的根源在于数学对象的“过程——对象”二重性.若把(1,3)∪(4,10)看作是数集(1,3)与数集(4,10)进行并集运算的过程,则a∈(-∞,4)∪(4,+∞)的确不规范;若把(1,3)∪(4,10)看作 是数集(1,3)与数集(4,10)进行并集运算的结果,则a∈(-∞,4)∪(4,+∞)没有任何问题.鉴于此,多个区间的“∪”可以作为定义域和参数取值范围的最终结果呈现. 1.理解数学是有效教学的前提 章建跃博士指出,“理解教材是当好数学教师的前提,而理解教材的第一要义是理解数学”.对中学数学教师而言,理解数学是有效教学的前提.这需要教师能够站在学科课程的高度,以学科知识的发生发展视角来审视教材,审视数学概念;能够站在高观点下看待初等数学,把握数学概念的本质,真正实现由教教材向用教材教转变. 2.善于反思,大胆质疑 3.充分挖掘概念的内涵 在概念教学中,“一个定义,几点注意”的教学方式曾受到很多人的抨击.这种教学方式固然有其不合理的地方,但还是需要批判性地继承与发展.作为一直贯穿整个高中数学的“区间”概念,试想在教学时,教师若能引导学生注意“a,b”的实数性,引导学生思考(-2,2)∪(5,8)是不是区间、是不是集合…学生是否就可以避免本文中提到的一些问题呢?这其实是对区间概念内涵“实数性”、“连通性”、“区间与集合的关系”的挖掘.三、收获:对区间概念的认识

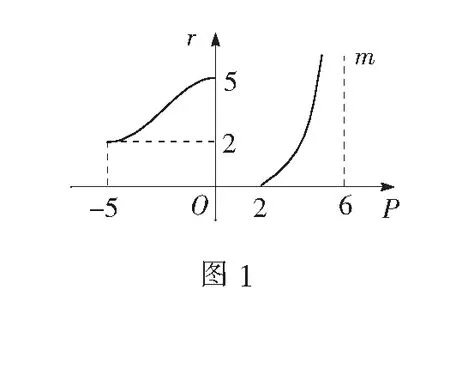
四、思考:由研读区间概念想到的