高中数学中向量问题的分类解析
2016-12-17傅君明
傅君明
(江苏省溧阳市光华中学(燕山部),213300)
高中数学中向量问题的分类解析
傅君明
(江苏省溧阳市光华中学(燕山部),213300)
在数学中我们把具有大小和方向的量称作向量.向量体现了几何与代数双重特性,使其具备了“数”与“形”的双重身份.正是基于向量的这一特点,使得向量成为解决几何、代数、物理问题的重要工具.向量重要的应用价值和复杂的基础逻辑使得它成为了高中数学的教学重点,特别是向量的应用更是重点中的难点.本文通过对向量应用类型的划分,帮助同学理顺向量的应用的实质,并结合例题剖析,优化解题思路,提升教学效率,提高教学质量.
一、与向量基本内容相关的运算
向量与其它数学概念最大的不同在于向量是既有大小,又有方向的量,所以在向量相关的计算中需要考虑影响结果的因素也相对较多.与向量基本概念和性质相关的题型相对基础,解题的前提是要求同学掌握系统的知识框架,对概念有清晰的理解,对运算规律及其几何意义要准确掌握,并充分把握好向量所体现的几何与代数的双重特性.
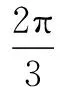
解析 对于本题而言,只要掌握向量的基础性内容即可.
(1)单位向量,即长度等于1的向量,所以|e1|=|e2|=1.
(3)结合已知条件和向量数乘运算:
a·b=(e1-2e2)·(ke1+e2)

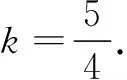
解析 对于本题而言,涉及的基础性内容有:
(1)平面向量的坐标运算法则.λa=(λx1,λy1)和a+b=(x1+x2,y1+y2).
(2)共线向量的定义及坐标关系.
在上述概念的基础上结合已知进行求解:
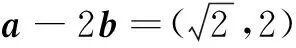
可见,对于考查向量相关基础理论的问题,首要是剖析题目涉及的知识点,同时结合已知条件进行解题分析.这类题型主要出现在填空和选择的部分,题目相对简单,但需要同学准确把握与向量相关的基础型内容.所以在教学中,老师要注重基础知识教学,帮助同学形成向量的概念、向量运算、实数与向量乘积、向量共线、平面向量等关键理论的知识网络,提升同学理解问题、解决问题的能力.
二、与平面解析几何相关的运算
平面向量与平面几何有着密切的联系,例如,通过向量夹角的判断可以推断几何图形的垂直关系,利用向量的坐标运算可以推断图形的位置关系,借助向量的数量积可以计算图形中角度的大小等.在高中数学中,向量的坐标运算是将几何问题代数化的重要工具,所以在教学中老师要注重学生“数与形”转化能力的培养,提升学生的逻辑思维能力.
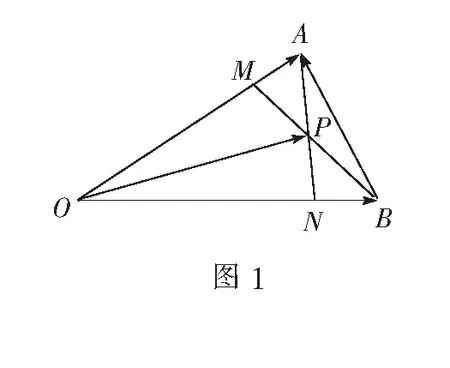
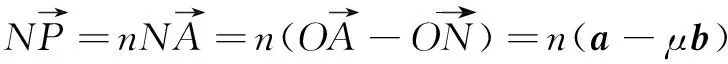
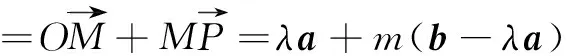

因为a和b不共线,且表示方法唯一,借助方程思想,有
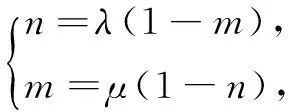
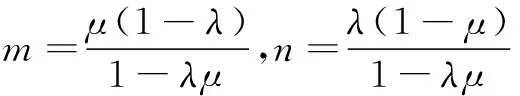
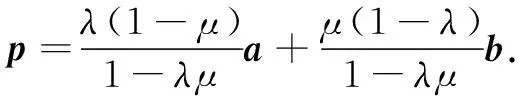
对于本题而言,解题的关键是建立起已知向量与未知向量的联系.在这个过程中要注意向量的方向性,所以结合向量的加法运算,将p准确地表示出来. 可见,在平面几何中利用向量和向量的运算规律可以表示出未知线段的数量关系.如将上题各个点赋予具体的坐标,则可以根据向量坐标的计算得出各个点在坐标中的位置关系.所以说向量运算过程对于研究平面几何相关的点、线关系有重要的意义.
三、与立体几何相关的运算
立体几何中,由于点、线、面、角在空间中的立体排布,使我们对图形的分析产生了不小的阻碍.而借助向量的相关性质和原理,特别是坐标间的相对关系,可以有效地判定两条异面直线所成的角,线与面所成的角,面与面所成的角等一系列问题.利用向量的知识来解立体几何的实质是将立体几何问题转化为平面问题来解决.只要在解题中把握好这一原则,同时注意向量的方向特性,向量就可以成为解决立体几何问题的有力工具.
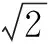
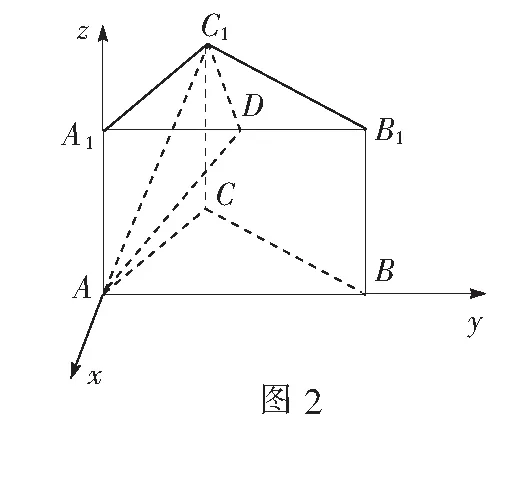
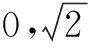
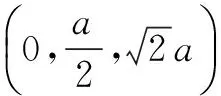
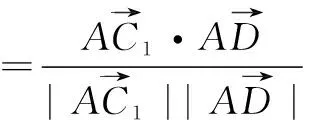
所以直线AC1与平面ABB1A1所成角大小为30°.
通过教学调研我们发现,与向量相关的立体几何的求解多与角的大小相关.所以在教学中,首要的是引导学生在脑海中形成立体中相关元素的位置转化思维.常用的方法是利用辅助线、中点关系将空间位置转变为平面关系.其次是根据夹角公式中涉及的向量关系,计算出向量的空间坐标,在这个过程中要充分地借助向量的加法关系、比例关系等等.最后,通过公式的准确运用和缜密的计算,得出所求角度的大小.通过以上三个环节,定能将立体几何相关的问题化险为夷,提升解题能力.
四、与其他数学知识的综合运用
通过上面的分析我们发现,向量运算中蕴含着丰富的数学逻辑和计算法则,所以完全可以为解决数学问题提供创新的思路.随着教学改革的深入,数学知识的综合应用能力逐渐成为考查的重点,这就需要老师在教学中变通教学方法,突出教学内容的相关与统一,为知识的全面应用打好基础.通过教学探究我们发现,平面向量的数量积与坐标间的数学关系,可以成为解决三角函数问题的有效方法.
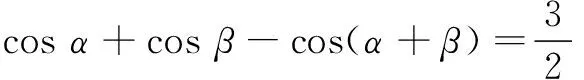
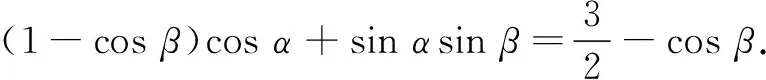
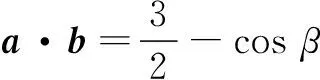
|a||b|
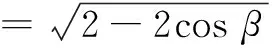
根据|a·b|≤|a||b|,有
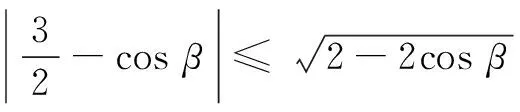
本题将三角函数的运算与向量的数量积相结合,创新了解题思路,大大简化了解题步骤,从而提升了解题效率.
当然,除上述例题外,向量在解方程、条件的最值计算中同样有着重要的应用.在应对这类问题时,老师需要帮助同学切实掌握向量相关的基础理论,剖析运算法则中的特点,启迪数学问题间的联系能力,帮助同学掌握数学解题中的转化能力.对于同学而言,要在解题中发散思维,根据题目变形和形式特点,联系相关内容,创新解题方法,注重知识的运用.
在向量教学的初期,受制于复杂题型的干扰,大多数同学对向量相关的题目深感困惑.本文通过向量的应用进行系统的分类,帮助同学整理一类学习素材,为学习向量提供了科学的借鉴.可见无论是向量基础理论的应用,还是与平面几何或是立体几何的“数形结合”,或是与其他数学知识的综合呈现,都需要以扎实的理论知识为基础,缜密的数学逻辑为思路,科学的解题策略为方法,只有这样,解决向量应用问题才能得心应手.
