管线钢平面应变断裂韧性经验模型研究

张 华，张 宏，王亚龙，赵新伟，李 娜

(1.中国石油大学(北京)，北京102249；2.中国石油集团石油管工程技术研究院石油管材及装备材料服役行为与结构安全国家重点实验室，西安710077)

管线钢平面应变断裂韧性经验模型研究

张 华1,2，张 宏1，王亚龙2，赵新伟2，李 娜2

(1.中国石油大学(北京)，北京102249；2.中国石油集团石油管工程技术研究院石油管材及装备材料服役行为与结构安全国家重点实验室，西安710077)

为了研究高钢级管线钢断裂韧性受试样厚度影响的变化规律，对X80管线钢不同厚度的试样进行了系列断裂韧性试验，建立了X80管线钢平面应变断裂韧性和临界壁厚关系的经验估算模型。基于试验结果以及三维断裂力学理论和准则，对所建立的经验模型进行了验证。结果表明，对于X80管材，平面应变的临界壁厚大约在50mm，与厚壁弯管的爆破试验结果基本吻合；经验估算模型的预测结果较为准确，能够满足工程应用的需要。

管线钢；断裂韧性；平面应变；厚度效应

1 概 述

对于受载的裂纹体，应力强度因子KI是描述裂纹尖端应力场强弱的力学参量。构件承受的载荷增大时，KI也随着增大，当KI增大到一个临界值时，带裂纹的构件就会发生断裂。这一临界值称为断裂韧性KC或KIC，代表了材料抵抗裂纹不稳定扩展的能力。断裂韧性KC或KIC则是材料本身的固有属性，两者不同点在于KC是平面应力状态下的断裂韧性，KC受试样厚度的影响，当厚度大于一个临界值后，裂纹尖端就处于平面应变状态，此时断裂韧性就基本不再随厚度的增加而变化，这时就是平面应变状态下的断裂韧性值，该值称之为KIC，或平面应变断裂韧性，此时该参数才是真正的材料常数，反映了材料阻止裂纹扩展的能力[1-2]。断裂韧性临界值随试样壁厚的变化规律如图1所示。

由于裂纹在尖端进入平面应变状态后，临界断裂韧性会显著降低，相同尺寸的裂纹在厚度较厚时更容易起裂。随着我国管道建设朝着高钢级、大直径、大壁厚的方向发展，已经大规模应用的高钢级管线钢断裂韧性是否达到平面应变状态，对管道安全运行是否会带来重要的影响，已经受到业界专家的关注。本研究通过不同厚度的断裂韧性试验，建立平面应变断裂韧性的估算模型，主要目的在于分析现有高钢级管线钢应用中的厚度是否达到平面应变状态，并采用三维断裂理论对模型进行了验证。

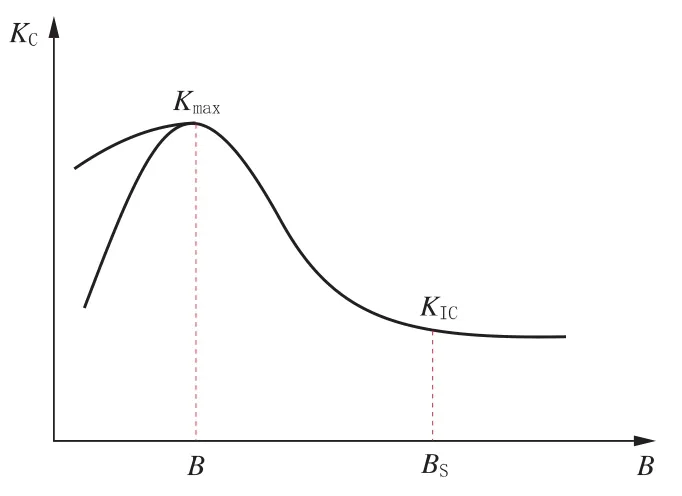
图1 断裂韧性随试样厚度的变化规律

2 不同厚度断裂韧性试验

断裂韧性试验所用的X80材料取自规格为Φ1 219mm×26.4mm直缝埋弧焊管，管材力学性能见表1。

表1 试验材料X80钢的力学性能

因材料厚度有限，此次试验采用紧凑拉伸试样(CT)。对于管道来说，环向应力最大，轴向裂纹最为危险，因此试样的预制裂纹方向平行于管道轴向。试样厚度B最厚为25mm、宽度W为50mm，厚度最厚的试样满足GB/T 21143[3]的规定。为了测试试样厚度对管材断裂韧性的影响，对X80管材分别选取厚度为25mm、22mm、20mm、18mm、16mm、14mm、12mm、10mm、8mm和6mm的试样，每组试样各3件，分别进行断裂韧性试验。

不同壁厚试样断裂韧性KC随试样厚度的变化规律如图2所示，图2中数据点为同厚度3个试样的平均值。

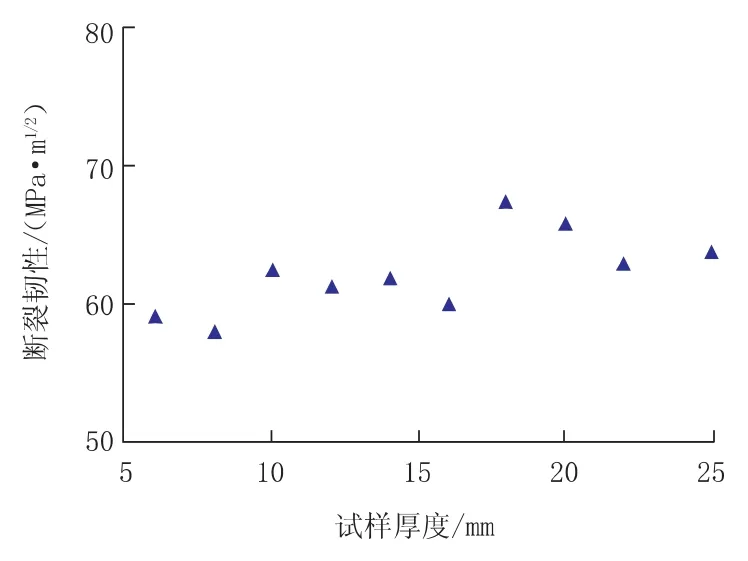
图2 断裂韧性KC随试样厚度的变化规律

3 平面应变断裂韧性估算模型

3.1 裂纹尖端塑性区半径

塑性区半径和厚度之比(rp/B)对裂纹尖端应力状态的影响较大。如果塑性区尺寸和试样厚度相当，那么rp/B就接近1，表明平面应力状态在试样的厚度方向上占主导地位；如果该比值远小于1，就说明平面应力区宽度只占厚度的很小一部分，试样厚度方向将以平面应变状态为主。根据已有的试验结果，当rp/B=0.025时，试样将进入平面应变状态[3]。

基于弹性解的平面应力状态裂纹尖端塑性区半径(θ=0)为

式中σs为屈服强度，将rp/B=0.025带入(1)式，并以平面断裂韧性值KIC代替KI，则可以求得平面应变的临界厚度为

3.2 断裂韧性与厚度的线性关系

Anderson[4]就已有的数据分析了厚度效应，他确定近似的认为KIC随着厚度而线性减小是合理的。Anderson对已有的断裂韧性数据进行了统计分析，主要材料为铝合金和钢铁材料。分析结果表明，在试样从平面应力向平面应变转化过程中，断裂韧性值与厚度的关系是可以用直线段来近似的。

取X80管线钢断裂韧性试验中KC由最大值开始减小的数据做图，即壁厚超过18mm试样的试验结果，对其断裂韧性随厚度的变化情况进行线性拟合，得到KC随壁厚的变化规律。在这里，将KC随壁厚的变化规律简化为线性变化。拟合得到的断裂韧性与试样厚度之间的线性关系表达式为

令KC=KIC，B=BS，则式(3)变为

求解式(2)和式(4)，计算BS和KIC，得到KIC=49.2MPa·m1/2，BS=48.7mm。经验模型求解思路如图3所示。

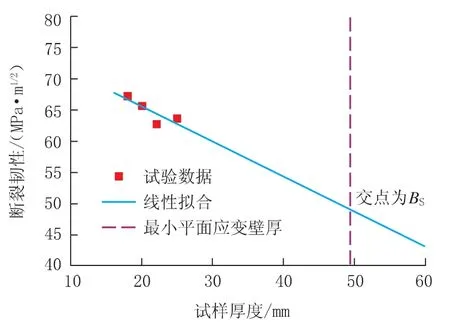
图3 经验模型求解思路示意图

4 经验估算模型验证

4.1 试验数据验证

采用文献[5-6]中的TC4钛合金断裂韧性数据进行初步验证。KIC的测试结果为58.82MPa·m1/2，本模型计算结果为54.57MPa·m1/2，结果相差7.2％。本模型计算的临界壁厚BS为22.9mm。文献中对此数据没有计算，不过以文献提出的计算公式来看，试样壁厚超过20mm之后，预测的断裂韧性值随壁厚的变化已经很小，可以认为裂纹尖端已经进入了平面应变状态。文献中对平面断裂韧性值是采用已知值进行拟合的，因此精度较高，但在平面应变韧性值未知的情况下就无法准确计算，或者说拟合精度会差一些。

在已经开展的X80弯管和三通的爆破试验中，当钢管壁厚超过50mm，爆破断口都呈现脆性断裂形貌，与经验模型预测的临界壁厚基本一致，因此，可以说X80管线钢的平面应变断裂韧性临界壁厚在50mm左右。

4.2 理论验证

已有的研究表明，裂纹尖端的三维应力应变场对材料断裂有着重要影响。离面约束是造成二维和三维问题差异巨大的主要原因，郭万林将其引入到已有的断裂力学理论中，建立了三维断裂力学的K-TZ和J-TZ双参数描述以及三维断裂准则。张斌等人进一步完善了基于离面约束的三维断裂力学理论，并在管线钢断裂评估中取得了较为成功的应用[7-20]。三维断裂准则表述如下[7]

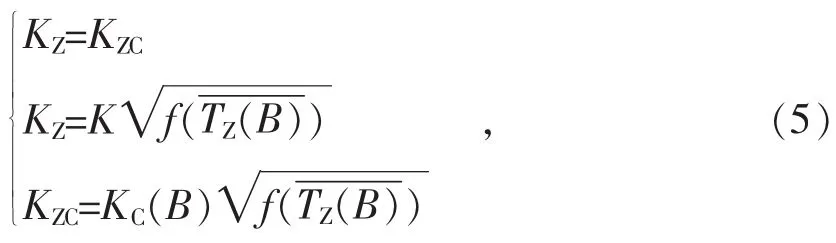
文献[11]根据有限元计算结果提出了针对I型穿透裂纹的拟合表达式

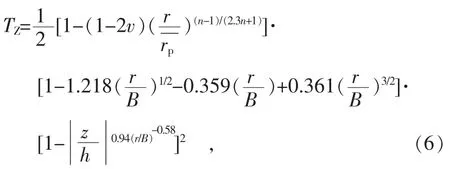
式中r为裂纹前端的极坐标半径，n为材料的Ramberg-Osgood硬化指数，为θ=0时裂纹尖端穿透厚度的平均塑性区尺寸，即

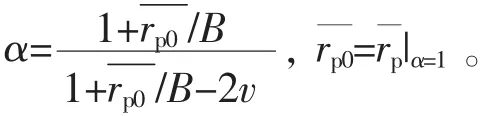
式中

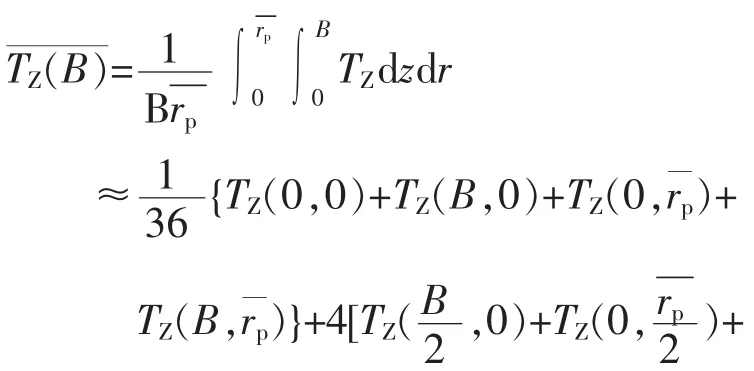
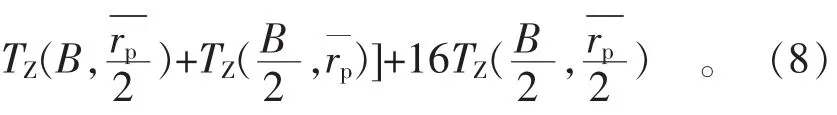
根据上述分析，分别对X80管材断裂韧性进行计算，取18mm厚度以后的试验值，结果如图4所示。KC的平均值为58.0MPa·m1/2，试验得到的KC与平均值的误差为8％～16％。KZC的平均值为143.53MPa·m1/2，通过换算得到的KZC与平均值的误差为0.12％～5.69％。通过引入离面约束因子，基本消除了厚度对断裂韧性的影响，KZC基本上可以作为代表材料性能的一个常量。经验模型得到的KIC换算成KZC之后，与KZC的平均值相差不大，说明经验模型对KIC的估算基本准确。

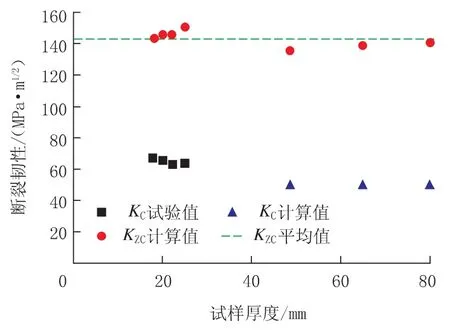
图4 平面断裂韧性经验模型的验证

断裂韧性预测值的误差分析如图5所示，50mm、65mm和80mm3个数据点是通过经验模型估算得到的，在经验模型中，认为当壁厚大于BS之后，壁厚的增加已经不能导致断裂韧性的降低。将上述3个预测值换算成KZC可以看出，3个数据点与KZC平均值的误差很小，尤其是80mm的试样。根据国标中对试样厚度的计算，当试样壁厚大于80mm，则完全满足平面应变测试状态，80mm试样的KC基本上可以看作KIC。

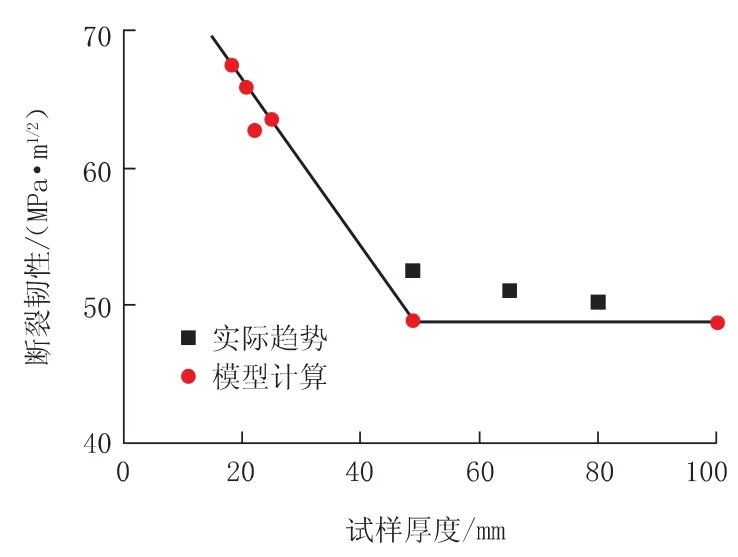
图5 断裂韧性预测值的误差分析

在壁厚为48.7mm时，断裂韧性KC试验值为49.2MPa·m1/2，换算成KZC时，与KZC平均值的误差为5.69％。误差是由于在经验模型中，采用了两段式的线性拟合(见图5)，而在实际中，随着壁厚的增加，KC随试样厚度的变化是非线性的，壁厚为48.7mm的试样，真实断裂韧性应该稍高于计算值。如果以KZC平均值反推KC值，在壁厚为48.7mm时，KC应该为52.49MPa·m1/2，与经验模型的误差在6％左右，误差在工程应用可接受的范围内。由于随着壁厚的增加，KC还会进一步降低，因此，以经验模型计算得到的48.7mm厚度下的KC，更接近实际的平面应变断裂韧性。由于断裂韧性KC和壁厚B之间的非线性关系，其本质是裂纹尖端平面应变区所占的比重逐渐升高，无限趋近于1的过程，因此无法确定一个准确的壁厚作为平面应变断裂韧性的临界壁厚。从试验数据和理论分析来看，在壁厚超过48mm之后，断裂韧性KC随厚度的变化已经不大，可以认为裂纹尖端已经进入平面应变状态。

5 结 语

通过对不同厚度试样的断裂韧性试验，分析了高钢级管线钢断裂韧性受试样厚度的影响规律，建立了平面应变断裂韧性和临界壁厚的经验估算模型，并采用已有的试验数据和三维断裂理论对经验估算模型进行了验证，验证结果相差6％～7％。对于X80管材，平面应变的临界壁厚大约在50mm，与厚壁弯管的爆破试验结果基本吻合。

管道工程干线用管最大壁厚远小于该临界壁厚，裂纹尖端尚未完全进入平面应变状态；对于壁厚较大的弯管和三通等管件，其厚度已经接近或者达到临界壁厚，因此在使用时应注意其安全性，特别是对于低温环境下使用的管件。此外，试样厚度对于高钢级管线钢的断裂韧性有明显的影响，对含裂纹缺陷结构剩余强度评价时，平面应变状态下的临界断裂韧性会导致偏于保守的评价结果。因此在断裂评估时，应考虑壁厚的影响，选择合适的断裂参量进行评估。

[1]赵建生.断裂力学及断裂物理[M].武汉：华中科技大学出版社，2003.

[2]D布洛克.工程断裂力学基础[M].北京：科学出版社，1980.

[3]GB/T 21143—2007，金属材料 准静态断裂韧度的统一试验方法[S].

[4]ANDERSON W E.Some designer-oriented view on brittle fracture[C]//Battelle Northwest Rept.SA-2290，1969.Houston，Texas：Gulf Coast Metals Conference，1969.

[5]杨继运，张行.含裂纹板断裂韧度厚度效应的理论研究[J].机械强度，2005，27(5)：672-680.

[6]杨继运，张行，张珉.含裂纹板断裂韧度厚度效应的理论与应用[J].机械工程学报，2005，41(11)：32-42.

[7]郭万林，于培师.构件三维断裂与疲劳力学及其在航空工程中的应用[J].固体力学学报，2010，31(5)：553-570.

[8]郭万林.三维断裂和疲劳裂纹扩展[D].西安：西北工业大学，1991.

[9]GUOW.Elastoplasticthreedimensionalcrackborderfield-I[J].Engineering Fracture Mechanics，1993，46(1)：93-104.

[10]GUO W.Elasto plastic three dimensional crack border field-II[J].Engineering Fracture Mechanics，1993，46(1)：105-113.

[11]GUO W.Elasto plastic three dimensional crack border field-III[J].Engineering Fracture Mechanics，1995，51(1)：51-71.

[12]GUO W.Three dimensional analysis of plastic constraint for through thickness cracked bodies[J].Engineering Fracture Mechanics，1999，62(4-5)：383-407.

[13]ZHAO J H，GUO W L，ZHANG B，et al.Advances in three-dimensional fracture mechanics[J].Key Engineering Materials，2006，312：27-34.

[14]张斌.材料结构宏观三维断裂和微观破坏行为研究[D].南京：南京航空航天大学，2005.

[15]董蕙茹，郭万林，杨政，等.管线钢非穿透裂纹体的断裂研究[J].金属学报，2001，36(6)：579-584.

[16]杨政，郭万林，董蕙茹，等.X70管线钢冲击韧性试验研究[J].金属学报，2003，39(2)：159-163.

[17]杨政，郭万林，董蕙茹，等.X70管线钢的断裂韧性[J].钢铁研究学报，2003，15(5)：40-45.

[18]郭万林，董蕙茹，杨政，等.厚度与分层的耦合效应对X60 管线钢断裂韧性的影响[J].金属学报，2001，37(4)：386-390.

[19]郭万林，董蕙茹，杨政，等.X60管线钢非穿透裂纹体的断裂研究[J].金属学报，2001，37(6)：579-584.

[20]杨政，郭万林，霍春勇.X70管线钢不同温度下断裂韧性试验研究[J].金属学报，2003，39(9)：908-913.

Study on Empirical Model of Plane Strain Fracture Toughness for Pipeline Steel

ZHANG Hua1,2,ZHANG Hong1,WANG Yalong2,ZHAO Xinwei2,LI Na2
(1.China University of Petroleum(Beijing),Beijing 102249,China；2.CNPC Tubular Goods Research Institute,State Key Laboratory of Performance and Structural Safety for Petroleum Tubular Goods and Equipment Materials,Xi’an 710077,China)

The high grade pipeline steel fracture toughness is affected by specimen thickness,in order to study the influence change rule,a series of fracture toughness tests were carried out for different thickness X80 pipeline steel specimen.The empirical estimation model between X80 pipeline steel plane strain fracture toughness and critical wall thickness was established.Based on test results and three-dimensional fracture mechanics theory and criterion,the empirical model was validated.The result showed that,for X80 pipe material,the critical wall thickness of plane strain is about 50mm,it is basic consistent with the blasting test results of thick wall bends;the predicating results of experience estimation model are more accurate,can meet the requirements of engineering application.

pipeline steel;fracture toughness;plane strain;thickness effect

TG113.254

A

10.19291/j.cnki.1001-3938.2016.08.003

张 华，男，高级工程师，主要从事油气输送管道的完整性管理技术研究及管材质量检验工作。

2016-04-19

谢淑霞

陕京四线输气管道工程正式开工

2016年8月8日，记者从中石油北京天然气管道有限公司了解到，陕京四线输气管道工程自7月11日在北京市和内蒙古自治区等标段进行设备调试、现场焊接试验后，于近日在乌兰察布市打火开焊，标志着这一国家重点工程全面开始现场建设。

陕京四线输气管道工程包括1条干线和高丽营—西沙屯、马坊—香河—宝坻、香河—西集3条支线。本期建设包括1条干线1条支线，总长1 114km。干线起自陕西省靖边首站，途经内蒙古、河北，止于北京市高丽营末站，全线隧道穿越4处、河流大型穿越6处、河流中型穿越35处、铁路穿越28处、高速公路穿越26处，设计年输量250亿m3。管道沿线设置红墩界、鄂尔多斯、托克托、乌兰察布和张家口5座压气站。

陕京四线输气管道工程是中亚进口气和国产气输送的重要通道，是“西气东输”战略通道的延伸，进一步优化全国管网总体布局。陕京四线的建设，对于增加华北地区天然气供应量、提升冬季调峰供气能力、治理大气污染将发挥重要作用。同时，这项工程将打通中俄东线及唐山LNG供应北京市场通道，改善北京供气格局，提高首都供气管道的网络化程度，增强供气可靠性和灵活性，并满足2019年北京世界园艺博览会、2022年北京—张家口冬季奥运会对清洁能源的需求。

为配合国家发布的“大气污染防治行动计划”，逐步消除重污染天气，中国石油加快推进项目建设。审议通过了关于建设陕京四线输气管道工程的议案，确保干线在2017年10月底前建成投产。

(罗刚摘自中国石油网)