空间飞行器内声源定位算法研究
2016-12-15夏加高李文新曹靚姝李泰国
夏加高, 李文新, 曹靚姝, 李泰国
(兰州空间技术物理研究所,兰州 730000)
空间飞行器内声源定位算法研究
夏加高, 李文新, 曹靚姝, 李泰国
(兰州空间技术物理研究所,兰州 730000)
空间飞行器内空间狭小,存在较大的语音混响现像,飞行器内乘员不带专用耳戴进行语音通话时,混响信号影响通话质量。利用声源方位的信号进行语音增强的方法可以抑制混响的干扰,获得较好的通话效果。常用的声源定位算法由于受混响的影响,很难对乘员的语音进行有效地定位。通过研究空间飞行器的语音传输特性,提出了基于相关系数波束形成算法,该算法利用波形的相似性来抑制混响的干扰。实验证明:算法具有较好的声源定位效果,为语音增强提供声源方位参数。
飞行器;声源定位;相关系数;波束形成;语音增强
随着我国航天事业的发展,载人的空间飞行器已经在太空中在轨运行。空间飞行器内乘员与地面人员的通话是通过语音单元完成的。由于空间飞行器内空间狭小,存在较大的混响现象,乘员可通过专用的耳戴来减少混响的影响。但是乘员在飞行器内长时间工作、生活,与不同舱段的乘员通话都要使用专用的耳戴,从而引起诸多不便。因此,研发消除混响的语音通话单元使乘员无需使用专用耳戴就可进行语音通话,给乘员带来了极大的方便。
空间飞行器语音单元由麦克风阵列采集语音信号,当获取声源的方向时,可以通过增强声源方向的语音信号来抑制混响的干扰[1],从而获得较好的通话效果。由于密闭狭小空间的混响较为严重,混响信号对声源信号的幅值和相位都有较大干扰,常规的波束形成算法、MUSIC算法等[2-8]都很难对声源进行准确的定位。
通过研究空间飞行器内混响声波的传输特性,利用声源信号的相似性和波束形成的原理,提出了基于相关系统的波束形成算法。
1 基于相关系数波束形成算法的定位原理
1.1 定位条件和模型
为方便算法描述,定位模型是基于二维平面的。并应满足以下条件:① 声源是点声源或近似点声源,若声源的振动面直径远远小于其声波的波长可近似地看作点声源;② 在提取的麦克风阵列中各阵元的信号无静音情况;③ 各声源在频域上是非相干的。
如图1所示,该定位模型麦克风等间距地排列在一条直线上,间距为d,设定麦克风T4为均匀线性麦克风阵列的中心,即声源对于麦克风阵列的相对位置均以T4为参考点。声源Si在单位模型中的坐标用角度和距离来表示,即(αi,ri),αi为声源到T4并与麦克风线阵所成的夹角,其范围为0~180°,ri为声源Si到阵列中心T4的距离。rin是声源Si到第n个麦克风阵元的距离,dn是第n个麦克风阵元到阵列中心的距离。图1中麦克风阵列中有7个麦克风,在工程应用中麦克风阵列的阵元越多,定位的分辨率越高,通常以阵列中心的麦克风为定位参考点。此算法中阵元数目M可以为奇数,也可以为偶数,但是基于阵列中心阵元对称性的考虑,M为奇数效果较好。
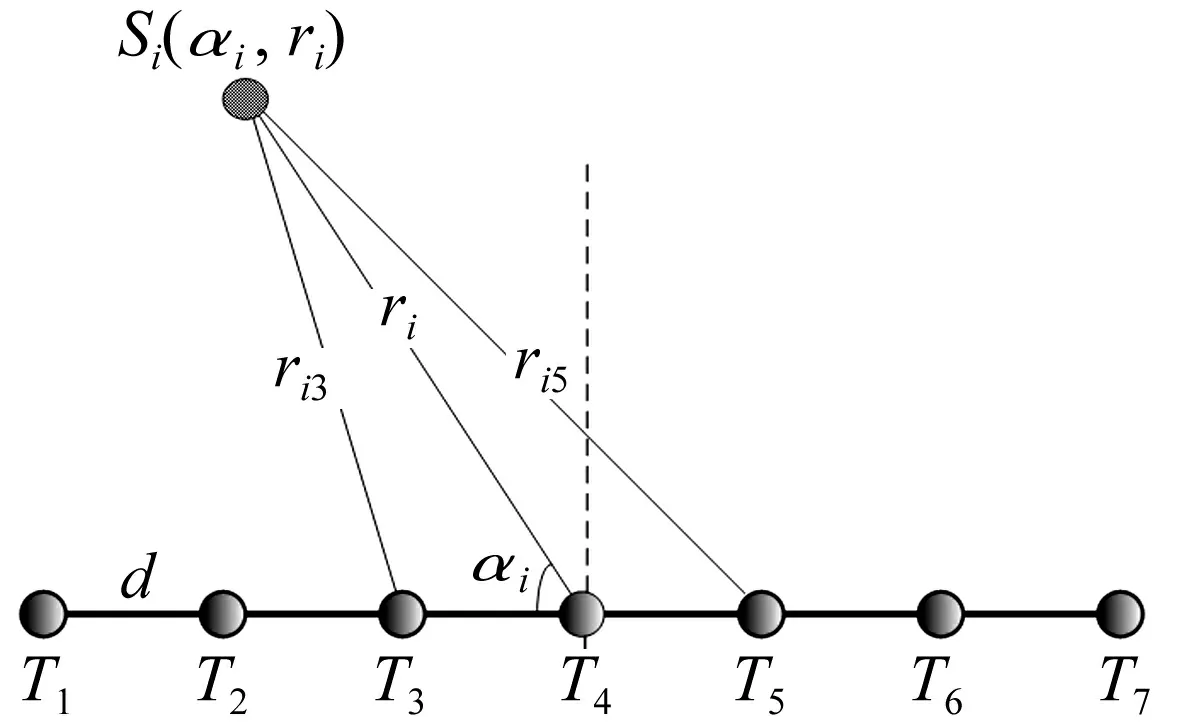
图1 声源定位模型Fig.1 Sound source positioning model
(1)
(2)
1.2 均匀线阵的近场和远场模型
根据声源到达麦克风阵列的距离,声音信号的传播模型可以分为近场模型和远场模型。
一般情况下,对于均匀线性阵列,当满足式(3)的条件时,声源可以视为远场模型来处理,反之则视为近场模型。
(3)
式中:r是声源到阵列中心阵元的距离,L为阵列孔径的大小,也就是均匀线阵的长度,λ是声源信号最高频率的波长,R为声源近场与远场临界距离。
近场模型中,声源到达麦克风阵列各阵元的入射角、幅值均不同,应采用球面波模型,需要考虑幅度衰减的因素。远场模型中,声源到麦克风阵列各阵元的入射角和幅值是相同的,声波可视为平面波。因此,空间飞行器内声源近场模型中。
1.3 混响条件下麦克风阵元的信号分析
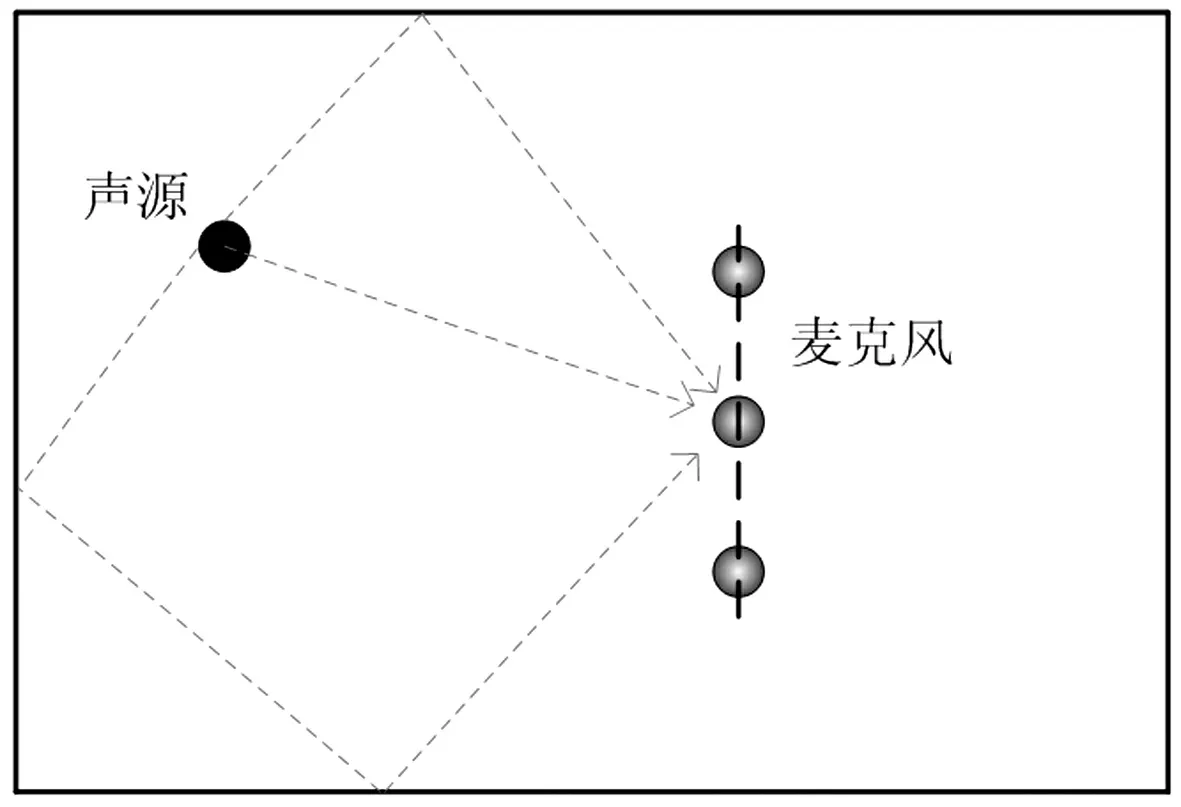
图2 混响模型Fig.2 Reverberation model
图2是密闭空间声源混响模型,麦克风i采集的声波信号不仅有直接来自声源的信号,还有来自其混响的声波信号,式(4)麦克风i在无混响环境下的数学表达式,式(5)是在两次声源反射条件下的数学表达式。
xi(t)=hi(t)*s(t)+wi(t)
(4)
(5)
式(4)中,s(t)是声源信号,hi(t)是无混响条件下的冲击响应,*是卷积,wi(t)是噪声。式(5)中s′是声源的一次反射信号,h′是其对应的混响冲击响应;s″是声源的二次反射信号,h″是其对应的混响冲击响应。通过式(4)和式(5)对比发现,在混响条件下,第i个麦克风采集的声音信号是相当复杂的,混响信号对声源信号的幅值和相位都有影响,且很难进行信号分离,因为混响信号与声源信号是相干的。如果用式(5)代替式(4)进行声源定位运算,不论使用什么算法,都不能得出正确的定位结果。
混响的大小与两个因素有关系,一是声源与阻挡物的距离,二是阻挡物与麦克风的距离。在狭小空间内,这两者的距离都很小,所以混响的能量较大。另一方面,麦克风阵列每个阵元到阻挡物的距离是不同的,所以混响占声源信号的能量比重也不相同。
虽然在混响环境中麦克风采集的声源信号的幅值和相位受到混响的很大干扰,但是声源信号的能量还是信号的主要部分,所以声源信号的基本形状没有改变。
1.4 波形相似性度量
本算法是利用波形的相似性来作为波束形成的对象,而波形相似性度量的主要方法是信号的相关分析。
信号的相关分析主要通过自、互相关函数、相关系数函数来完成。
(6)
(7)
(8)
自相关函数如式(6)所示,反映了同一信号在不同时刻的取值之间的相关程度。互相关函数如式(7)所示,反映了两个不同信号在不同时刻的相关程度,当两个信号在不同时刻完全相关时,其函数值最大。两个不同信号的函数取值的大小影响相关函数的计算结果,因而比较不同的成对的信号的相关度时,仅看其互相关函数值是不准确的。为了避免信号的幅值对其相关程度度量的影响,将相关函数作了归一化处理,这就是相关系数函数,见式(8)。
相关系数ρxx(τ)的值域为[-1,1],ρxx(τ)为0时,认为两个信号完全不相关;ρxx(τ)为1时,表明两个信号完全相关;ρxx(τ)为-1时,表明两个信号完全负相关。相关系数越趋于1,说明两个信号越相似。
1.5 基于相关系数的波束形成定位原理
基于相关系数的波束形成算法的基本思想是:在声源搜索区域内,麦克风阵列各阵元信号通过延时估计,与中心阵元信号进行相关系数运算并进行累加,得到一个关于相关系数的二维函数。当延时估计符合声源传播特性时,相似程度是最大的,此时取得极大值。即二维函数的极大值处,就是声源的位置。该算法是利用阵元信号的相似性识别声源方位,麦克风阵列各阵元信号均可作为参考信号,为数学表达方便,取中心阵元信号作为基准信号。
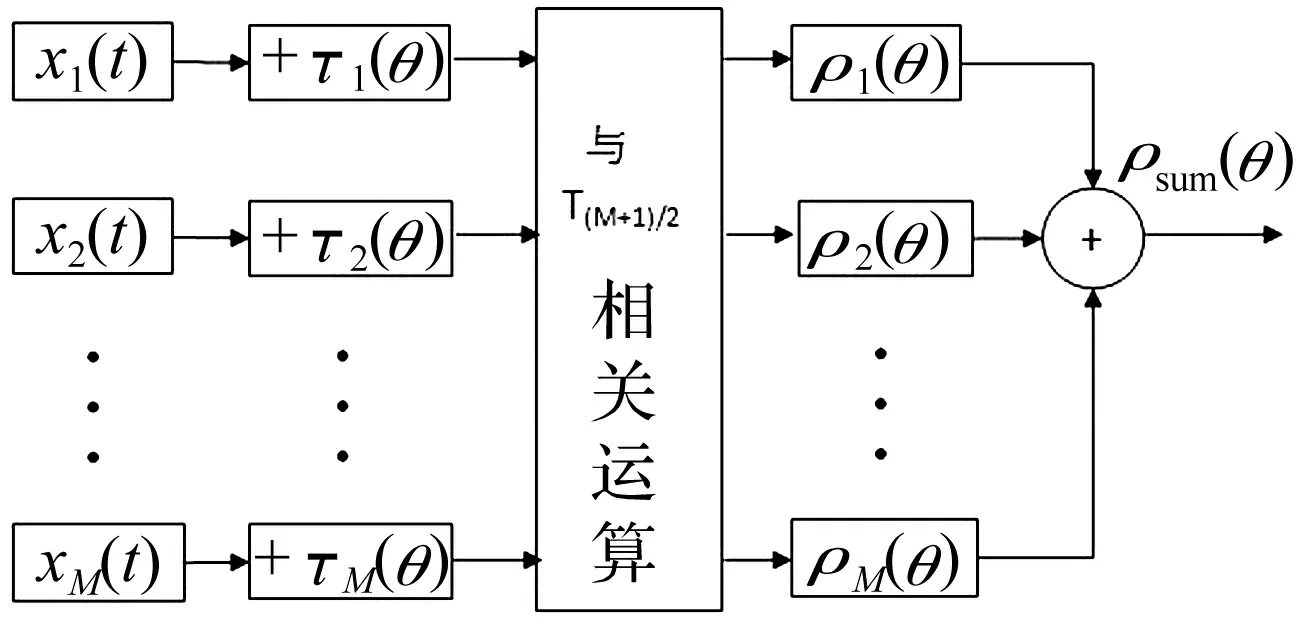
图3 基于相关系数波束形成算法Fig.3 Beamforming algorithm based on correlation coefficient
(9)
ρi(θ)=CORR(x(M+1)/2(t),xn(t-τn(θ)))
(10)
(11)
图3为基于相关系数的波束形成算法框图。xn(t)是麦克风阵列第n个阵元的声压信号。假设声源相对于麦克风阵列中心的入射角为θ,τn(θ)是麦克风阵列中第n个阵元相对中心位置麦克风的相对时延,ρn(θ)是麦克风阵列中第n个阵元经过时延操作后与中心位置麦克风信号的相关系数,ρsum(θ)是各阵元与参考信号的相关系数之和。
时延估计是通过搜索的方法得到的,角度的范围为0~180°,距离的范围为0~R。搜索的声源角度和距离通过时延估计、相关系数累加运算即可得到一个相关系数之和,称之为相关系数波束值,从而可以得到一个二维的相关系数波束图。单个声源定位时,相关系数波束图中的极大值对应的位置是声源方位;当多声源定位时,相关系数的波束图中相关系数极大值的个数即是声源的个数。
核心算法的伪指令程序如下:
FORD=0~RSTEP 10
搜索距离为0~R,步长为10 cm。
FORθ=0~180°
搜索角度为0~180°,步长为1°。
FORn=1~7n≠4
依次计算各阵元与中心阵元的相关系数
Tn的时延估计τ,并进行时序移动
与中心阵元做相关得到相关系数ρn(θ)
NEXTn
ρsum(θ)=ρ1(θ)+ρ2(θ)+ρ3(θ)+
ρ5(θ)+ρ6(θ)+ρ7(θ)
相关系数求和
NEXTθ
CORR (D:0~180°)=ρsum(θ)
给二维数组赋值
NEXTD
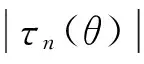
因为信号之间的相似度与幅值没有关系,所以在以信号相似度为波束搜索目标时,各阵元的权重是相同的。
2 基于相关系数波束形成算法声源定位过程
基于相关系数的波束形成算法的声源定位主要有以下几个步骤:布置麦克风阵列,数据采集及滤波,数据序列截取,相关系数波束形成,波束图平滑处理及峰值搜索。
2.1 布置麦克风阵列模型
根据图1的定位模型布置麦克风的位置,确定麦克风的数量、间距。在硬件允许的条件下,麦克风的数量越多,定位精度越高;麦克风的间距越小,其可以定位的声源信号带宽越大。麦克风的间距应小于声源最高频率的λ(波长)。如果麦克风的间距为10 cm,那么可以定位的声源频率范围应小于3 400 Hz。
2.2 数据采集及滤波
为了能更精确地定位,应使用高AD转换位、高采样率的数据采集装置。在进行数据采样时,为了方便后续的时延估计和信号处理,应选择合适的采样率,即合适的采样间隔,如采样间隔取10 us、20 us、40 us等。
在选择AD转换的采样率时,不仅要考虑满足时域信号采样要求,还要满足空域信号的采样要求。假设相邻麦克风的间距为10 cm,则两麦克风信号的最大时延约为290 us,如果采样间隔为100 us,时延估计的误差将接近100 us,如果采样间隔为10 us,时延估计的误差仅为10 us左右。
麦克风信号中不仅有声源信号、混响信号,还混入了一些白噪声,这些白噪声将影响定位精度,必须对这些白噪声进行滤波处理。由于声音信号的频率较低,在工程应用中一般选择低通数字滤波器。为使滤波后的信号不产生相位失真,这里选用FIR低通滤波器。
2.3 数据序列的截取
数量采集装置每次采集的数据长度较大,不可能完全参与相关运算和波束形成运算,因此必须要截取一定长度的数据序列。但是截取的数据长度不是任意的。
首先,截取的数据序列长度与麦克风阵列的长度有关,根据麦克风阵列的长度和AD采样率,可以得到一个最小截取长度。设麦克风阵列的长为L,则声波通过此阵列最大时长为:τ=L/v,设数据采集卡的采样间隔为t,麦克风阵列的各阵元与中间的阵元做相关系数运算,最小截取长度不少于τ/2t个数据点。如果麦克风阵列的阵元为7,阵元间距为10 cm,采样间隔为20 us,声速为340 m/s,则截取的数据长度应不少于45个点。
其次,所截取的数据不能有过多的静音信号。如果截取数据的静音信号较长,等于是加入非声源信号数据参与运算,定位肯定不准确。在定位过程中,应在声源连续发声时进行数据采集,这样才能保证截取的信号不含有过多的静音信号。
2.4 得到相关系数波束数据
根据截取的数据,利用相关系数形成算法,得到一个相关系数波束的二维数组。
离散数据序列的相关系数计算公式如:
(12)
2.5 波束图处理及峰值搜索
在复杂声场中,得到的波束图往往是不平滑的,在进行自动峰值搜索时会得到虚假的峰值,会出现虚假定位的情况,因此要对波束图进行平滑处理,这里采用的是移动加权平均法。波束图中的峰值所对应的角度即是声源的方位。这里的峰值不是波束图的最大值,而是极大值。
3 仿真实验及算法改进
3.1 单声源定位仿真
根据图1的定位模型,麦克风阵列有7个阵元,阵元间隔为10 cm。设声源Si到阵列中心与麦克风阵列的夹角为30°,到阵列中心的距离为60 cm。设声源信号中含有400 Hz、600 Hz、800 Hz频率成分,各频率成分的幅值和相位均不相同。根据声波的传播原理,从而得出每个传感器的声压信号,并叠加混响和噪声。混响中含有一个一次声源反射源和一个二次声源反射源,其模型如图2所示。xi(t)是第i个阵元含混响和噪声的信号,见式(13)。在近声场中,声波为球面波,声速为340 m/s,si(t)是声源到第i个阵元的信号,ri是声源到第i个阵元的距离,见式(14)。式(15)是第i个阵元一次反射声源信号表达式,A是一次声源的衰减系数,同理式(16)是第i个阵元二次反射声源信号表达式,A′是二次反射声源的衰减系数。
(13)
(14)
φ1=2×400π*20/340+0.25π
φ2=2×600π*20/340+0.5π
φ3=2×800π*20/340
(15)
γ1=2×400π*(20+60)/340+0.25π
γ2=2×600π*(20+60)/340+0.5π
γ3=2×800π*(20+60)/340
(16)
假定每个麦克风通道的采样率均为50 kHz。图4是合成后的第i个阵元的声压信号,横坐标为时间(s),纵坐标为声压(V)。
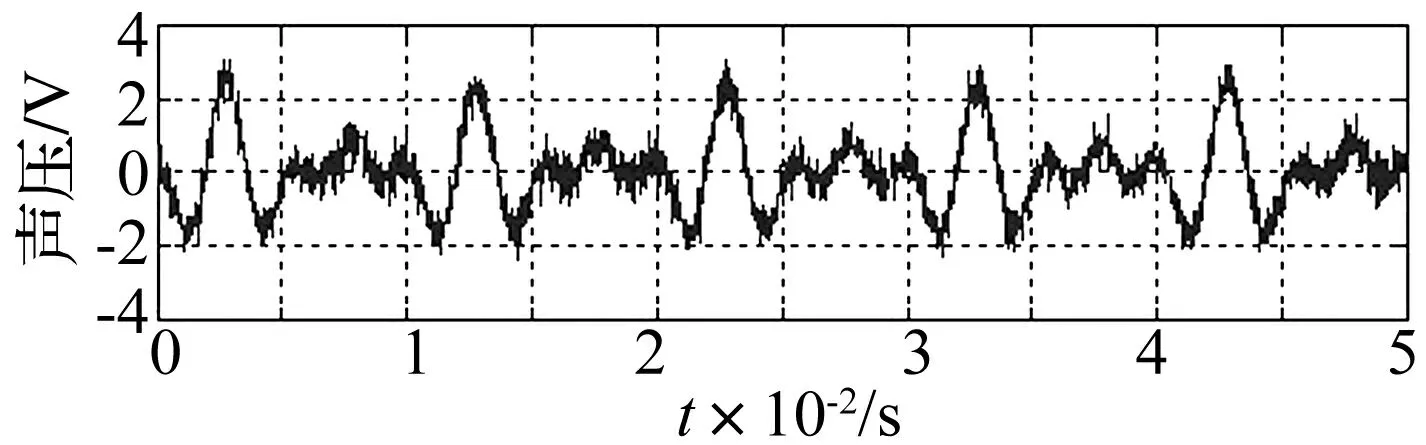
图4 声压信号Fig.4 Sound pressure signal
每个阵元信号的截取长度为1 ms,50个采样点,与阵元中心信号做相关系数运算。根据相关系数波束形成算法,得到一个相关系数波束形成二维数组。图5是相关系数波束形成的三维图形,为了使三维图形更加直观,对三维图形做了锐化处理。
从图5中可以看出,在20°~40°之间出现了一个“山脊”,这个“山脊”所对应的角度即是声源到阵列中心的入射角。同时在这个“山脊”之上,有一个“山峰”, “*”号标识处即为“山峰”,“山峰”在xoy平面上的投影即是声源的位置。
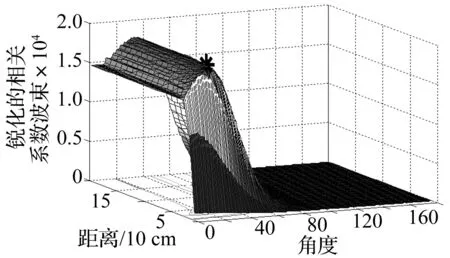
图5 相关系数三维波束形成图Fig.5 3D beamforming chart based on correlation coefficient
表1和表2是不同信混比的声源定位结果。A是一次反射声源的衰减系数,A′是二次反射声源的衰减系数,α,r分别是声源到阵列中心的角度和距离。仿真实验表明:一次反射声源对定位结果影响较大,当一次声源衰减系数A<0.3时,定位结果的角度、距离有较好的精度;当一次声源衰减系数A>0.3时,相关系数三维波束图会出现多个山峰,即会搜索出多个声源,定位精度下降;当一次声源衰减系数A>0.5时,则无法进行声源定位。

表1 不同信混比的定位结果
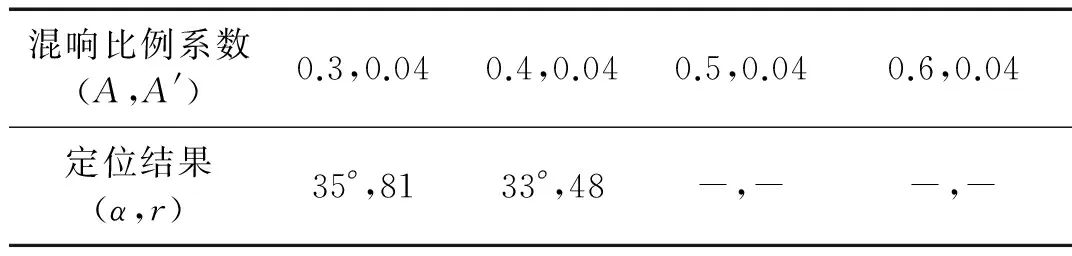
表2 不同信混比的定位结果
3.2 算法改进
在实际工程应用中,如果得到一个二维相关系数波束形成数据,计算量是很大的,实时性就较差,因此必须对算法进行改进。
通过以上的仿真数据可以发现,不同的搜索距离,得到的入射角是不同的,见表3和表4所示。但是可以发现一个规律,当搜索距离大于声源实际距离时,得到的入射角度基本不变。这是因为搜索距离D大于声源距离ri时,τn(θ)的变化不大。因此,D可以先定位为R,得到一个入射角,根据这个入射角搜索ri,然后用ri再搜索入射角,就是准确的声源位置。这样就大大减小了运算量。

表3 不同搜索距离的声源入射角

表4 不同搜索距离的声源入射角
设麦克风阵列的阵元数为M,参与相关运算的的数据个数为N,角度搜索范围为0~180°,距离搜索次数为L次。根据式(12)的离散数据的相关系数计算公式得,两组N个数据做相关得到的计算量为:(N×N+2)次实数乘法运算。所以未改进算法的计算量为(M-1)×180×L×(N×N+2)次实数乘法运算,加上180×L次比较运算。改进算法的计算量为(M-1)×180×(N×N+2)次实数乘法运算,加上180+L次比较运算。因此,改进算法节省了大量运算步骤。
在工程应用中,麦克风阵列的阵元数为7,参与运算的数据长度为50,角度搜索范围为0~180°,距离搜索次数为30。CPU型号为TMS320C6415,主频为500 MHz,1个时钟周完成1次实数乘法算法,改进算法所需时间为5.4 ms,见式(17)。空间飞行器的语音单元每60 s搜索一次声源方位并进行语音参数修正,式(17)的计算结果可以满足工程应用中的实时性要求。
t=5.4 ms
(17)
4 室内声源定位实验
4.1 单声源定位实验
单声源定位实验主要是验证算法的工程应用的可行性,并对算法进行改进。麦克风阵列由7个间隔为10 cm的麦克风阵元组成,麦克风的数据采样率为50 kHz。
声源定位环境如图6所示,声源和麦克风阵列周围有工作台,混响较大,表3为声源在麦克风阵列60°方位的定位结果。

表5 不同截取位置的定位结果

图6 单声源定位实验Fig.6 Single sound source localization experiment
从表5的实验结果中可以看出,截取不同位置的数据进行声源定位,会得到不同定位结果。图7是麦克风阵列中间阵元的信号,图中采样数据的开始处为静音信号,此信号不是声源发出的信号,要得到准确的定位结果,必须将静音信号的影响降到最低。简单的办法是增加参与定位运算的数据长度,以减小静音信号的比重。但这种方法会大大增加运算量。最好的办法是增加静音检测,不在静音信号处截取信号进行声源定位运算。
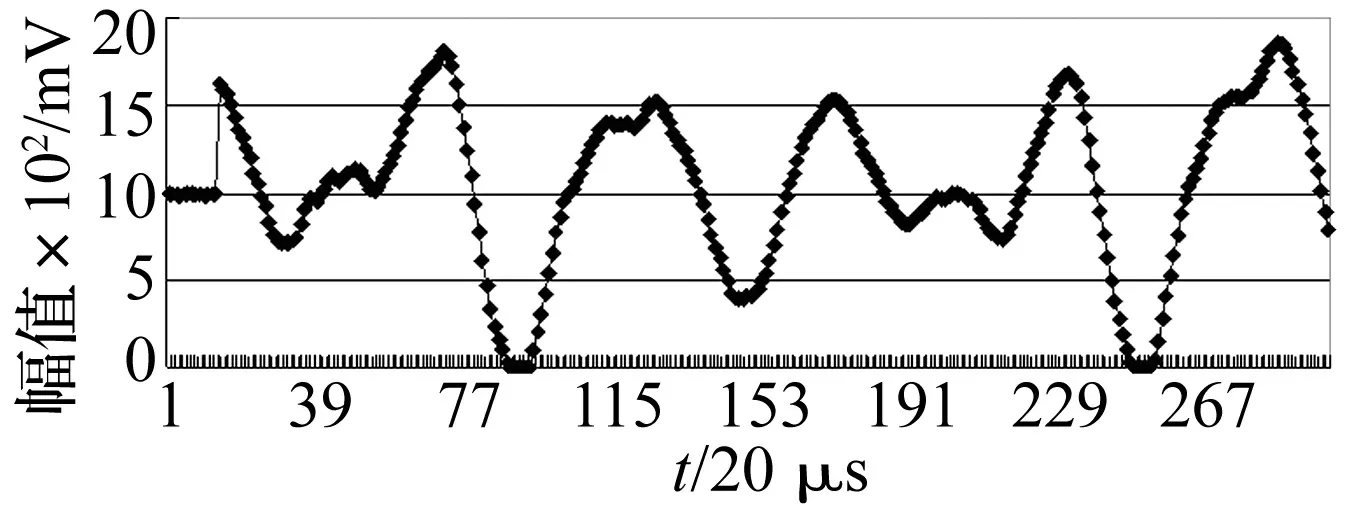
图7 声源信号Fig.7 Sound source signal
通过实验发现,声源的入射角在麦克风阵列的90°附近时,定位精度较差。通过分析知,声源在麦克风阵列90°附近时,声源到各阵元的距离差较小,50 kHz采样率不足以分辨较小距离差的信号差别,所以,会出现定位精度较差的情况,如表6所示。解决的方法是提高麦克风信号的AD采样率。

表6 不同声源入射角的定位结果
4.2 多声源定位实验
多声源定位是声源定位的难点,可以检验算法的有效性。室内混响环境中,在距离麦克风阵列中心1 m、入射角度为120°处,放置一个喇叭;在距离麦克风阵列中心1.4 m、入射角度为50°处,放置另一个喇叭。两个喇叭播放不同的音乐,用声源定位系统对两个声源进行定位。实验场景见图8所示,图9是声源定位结果。定位结果表明:基于相关系统的波束形成算法在混响环境中具有较好的多声源分辨能力。

图8 双声源定位实验Fig.8 Localization experiment of double sound sources
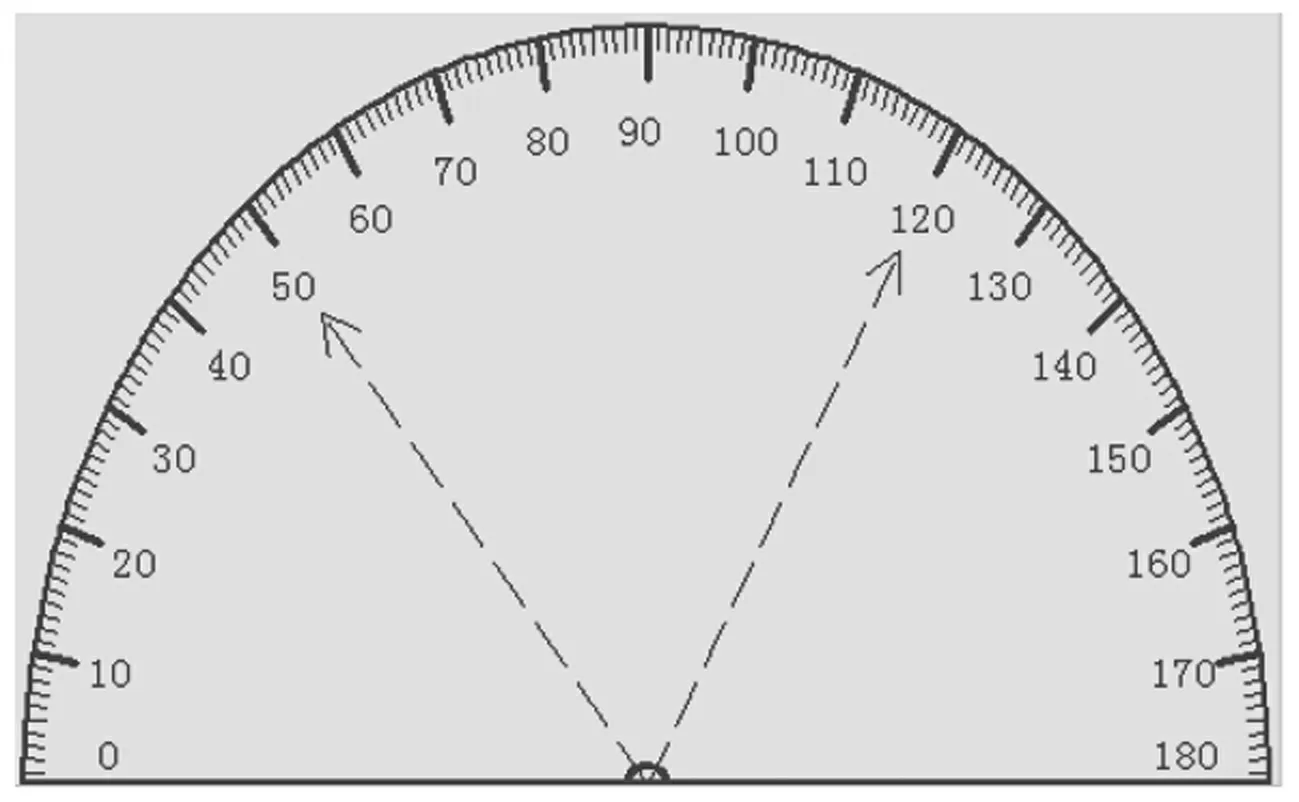
图9 双声源定位结果Fig.9 Localization results of double sound sources
5 结 论
本文针对狭小空间内声源定位的难题,提出了基于相关系数的波束形成算法,并对算法进行了改进,提高了定位的实时性。实验结果表明:该算法可以在混响环境中进行声源定位。但是为获得较好的定位精度,需要满足以下两个条件:① 消除静音信号对定位结果的影响;② 提高麦克风信号的AD采样率。
[1] 王冬霞,殷福亮. 基于近场波束形成的麦克风阵列语音增强方法[J].电子信息学报,2007,29(1):67-70. WANG Dongxia, YIN Fuliang. A nearfield beamforming method for microphone array based on speech enhancement[J]. Journal of Electronics & Information Technology, 2007, 29(1):67-70.
[2] 李芳兰,周跃海,童峰,等. 采用可调波束形成器的GSC麦克风阵列语音增加方法[J].厦门大学学报(自然科学版),2013, 52(2):186-189. LI Fanglan, ZHOU Yuehai, TONG Feng,et al. Microphone array speech enhancement based on adjustable beamformer generalized sidelobe canceller [J]. Journal of Xiamen University(Natural Science), 2013, 52(2):186-189.
[3] YO HAN K O, YEUNG J K, HYUN I Y, et al. 2-D DOA estimation with cell searching for a mobile relay station with uniform circular array[J]. IEEE Trans Communication,2010,58(10):2805-2809.
[4] VOLODYMYR V. Improving the performance of root-MUSIC via pseudo-noise resampling and conventional beamformer[J]. Microwaves, Redar and Remote Sensing Symposium, 2011, 25(8):309-312.
[1] 王楷,宗志亚,孙小惟,等. 改进的自适应特征值分解声源定位算法研究[J].仪器仪表学报, 2013, 34(6):1241-1246. WANG Kai, ZONG Zhiya, SUN Xiaowei,et al. Study on improved adaptive eigenvalue decomposition algorithm for acoustic source localization[J]. Chinese Journal of Scienfic Instrument, 2013, 34(6):1241-1246.
[6] WIDROW B, LUO F L. Microphone arrays for hearing aid: an overview[J].Speech Communication,2003,39(1/2): 139-146.
[7] BELOUCHRANI A, AMIN M G. Time-frequency MUSIC[J]. IEEE Signal Processing Letters, 1999, 6(5): 109-110.
[8] 蔡晶晶,李鹏, 赵国庆,等. RD-MUSIC的二维DOA估计方法[J]. 西安电子科技大学学报(自然科学版), 2013, 40(3): 81-86. CAI Jingjing, LI Peng,ZHAO Guoqing,et al. Two-dimensional DOA estimation with reduced-dimension MUSIC[J]. Journal of Xidian University(Natural Science), 2013, 40(3): 81-86.
Localization algorithm for sound sources in space aircrafts
XIA Jiagao, LI Wenxin, CAO Jinshu, LI Taiguo
(Lanzhou Institute of Physics, Lanzhou 730000, China)
There is a larger sound reverberation phenomenon because of a narrow space in a space aircraft. The reverberation signal influences call quality when crew members don’t wear the special earphone for voice calls within the aircraft. The use of a sound source location signal for speech enhancement can suppress reverberation interference to achieve a better call effect. Due to influences of reverberation, a common sound source localization algorithm is very difficult to get an effective location for the voice of a crew member. Here, through studying the speech transmission characteristics of the space aircraft, the beamforming algorithm based on correlation coefficient was proposed and the waveform similarity was used to suppress reverberation interference. Experimental results showed that the algorithm has a better effect of sound source localization to supply source orientation parameters for speech enhancement.
aircraft; sound source localization; correlation coefficient; beamforming; speech enhancement
中国载人航天工程重大专项(RWZY640601);国家自然科学基金(61125101)
2015-12-31 修改稿收到日期:2016-03-19
夏加高 男,博士生,工程师,1978年9月生
李文新 男,研究员,博士生导师,1966年生
TN912.3
A
10.13465/j.cnki.jvs.2016.21.032
