不同坡面角度碎石土斜坡动力响应特征研究

梁双庆， 苏立君， 王 洋

(1.中国科学院 水利部成都山地灾害与环境研究所中国科学院山地灾害与地表过程重点实验室，成都 610041；2.西安建筑科技大学 西部建筑科技国家重点实验室(筹)，西安 710055;3.中国科学院 青藏高原地球科学卓越创新中心,北京 100101; 4.中国科学院大学 研究生院，北京 100049)



不同坡面角度碎石土斜坡动力响应特征研究

梁双庆1,4， 苏立君1,2,3， 王 洋1,4

(1.中国科学院 水利部成都山地灾害与环境研究所中国科学院山地灾害与地表过程重点实验室，成都 610041；2.西安建筑科技大学 西部建筑科技国家重点实验室(筹)，西安 710055;3.中国科学院 青藏高原地球科学卓越创新中心,北京 100101; 4.中国科学院大学 研究生院，北京 100049)

设计并完成比例1∶100的小型振动台模型试验，坡面角度为35°、45°、55°，在满足相似律的条件下，输入不同频率X，Z双向正弦波，研究碎石土斜坡动力响应规律和变形破坏特征。结果表明高程对地震波具有放大作用；水平向加速度峰值放大效应强于竖直向；随着坡面角度增大，水平向或竖直向加速度峰值高程放大效应先增强后减弱，45°时最显著；坡体下部水平向加速度峰值随高程缓慢上升，坡体上部快速上升；竖直加速度峰值在整个高程内上升，无明显分界；随频率增大，坡体内同一高程水平向加速度峰值变大，竖直向加速度峰值先增大后减小，25 Hz时高程放大效果最明显。PIV结果表明坡度为45°，频率为25 Hz时，坡肩水平向运动最剧烈。碎石土斜坡易发生坡肩破坏。

地震；碎石土斜坡；动力响应；坡面角度；变形破坏

地形对斜坡在地震作用下的动力响应具有重要影响，主要表现在两个方面，斜坡的高度和坡度[1]。目前，国内外关于坡高对地震动力响应的影响的研究较多。DAVIS等[2]对San Femando地震的监测中发现斜坡对地震波具有显著的高程放大效应。高野秀夫[3]提出坡顶在地震作用下的最大位移为坡脚的7倍。王存玉[4]提出边坡顶部对地震具有显著的放大现象(垂直放大)。

坡度对地震动力响应的研究多集中于统计和数值模拟方面。韩宜康[5]统计汶川地震中发生的滑坡事件，提出是坡面角度为45°以上斜坡易发生地震滑坡。许冲[6]提出芦山地震中很多斜坡的坡度大于50°，一些区域的自然斜坡甚至近直立。田颖颖[7]提出鲁甸地震中很多滑坡发生在坡度为30°～50°或大于50°。丁彦慧[8]根据地震资料统计分析发现坡度小于 20°和大于 50°的斜坡很少发生滑坡；大多数滑坡发生在 30°～50°。祁生文[9]利用数值模拟分析得到坡度变化对加速度放大系数等值线图的分布形式有明显影响，但与边坡动力响应节律性变化无关。朱元清[10]采用有限元模型地震波传播，在SH波入射情况下，山脊及峡谷的倾角越大系数越高。周红[11]采用谱元法建立二维SH波传播模型，结果表明随着山体坡度增加，放大倍数明显变大。陈建君[12]通过数值模拟发现斜坡的地震动力响应与坡度呈非线性关系，在20°～50°的斜坡地震响应更明显，45°坡顶加速度响应值最大。

碎石土滑坡常常是填士、残积、坡积、崩塌或滑坡堆积以及硬岩全风化物等成因的松散堆积土形成的结构松散的斜坡[13]，是一种介于岩体和土体之间的特殊岩土体，具有大空隙、透水性强、强度低、稳定性差等特点[14]，是西南地区一种常见的滑坡类型，严重威胁交通、水利水电工程等基础设施的安全。因此，深入了解碎石土滑坡在地震作用下的动力响应规律，不但对研究碎石土滑坡的变形破坏机理及稳定性评价具有重要意义，而且对于该类滑坡的预防和治理具有重要的参考意义。但目前针对碎石土斜坡动力响应的研究成果尚不多见。

因此，本文采用小型振动台试验，在试验模型中布置加速度传感器、坡肩布置高清摄像机，旨在研究坡面角度和地震频率对碎石土斜坡动力响应规律及变形破坏特征的影响，为碎石土斜坡失稳机理的研究及防治工程的优化提供依据。

1 试验设计

1.1 试验设备平台

本试验在中科院山地所山地灾害重点实验室提供的二维小型振动台系统上进行。振动台主要由台面基座、振动弹簧、激震电动机、调频箱组成。地震波为正弦波，调频范围0.5～50 Hz，方向为X和Z向。水平X方向可输入最大加速度0.8 g，竖直Z方向可输入最大加速度0.6 g。

为了研究不同地震频率条件下斜坡的动力响应特征，采用正弦波频率为15 Hz，20 Hz，25 Hz，30 Hz及35 Hz，方向为X和Z向，振幅为0.2 g，振动时间为20 s。

1.2 相似关系设计

本试验模拟碎石土斜坡动力响应问题，相似关系设计主要考虑以下因素：

(1) 必须考虑重力场对试验的影响，SG=1。

(2) 必须考虑动力条件下边坡模型材料力学特征的相似性。以模型长度、密度和加速度为控制量，按Buckingham π定理导出各物理量之间的相似关系，如表1。

表1 模型试验相似常数

1.3 试验模型

模型箱宽为0.57 m，高为1.2 m，长为1.8 m，采用钢架结构固定边界，侧壁为双层玻璃，内侧为有机玻璃，为侧为钢化玻璃，二者之间的四周用弹力很好的胶层夹膜来起到增加阻尼减少波的回弹作用，以消除试验过程中产生的边界效应。

斜坡材料采用理县某滑坡后缘原位土，按等质量代换法按SL237—1999土工试验规程对级配中超粒径颗粒进行计算和代换，级配如图1。2 mm以上的颗粒累积质量含量大于50%，为碎石土。含水率为12%，容重为19.60 kN/m3，内摩擦角为39.6°，黏聚力40.08 kPa。

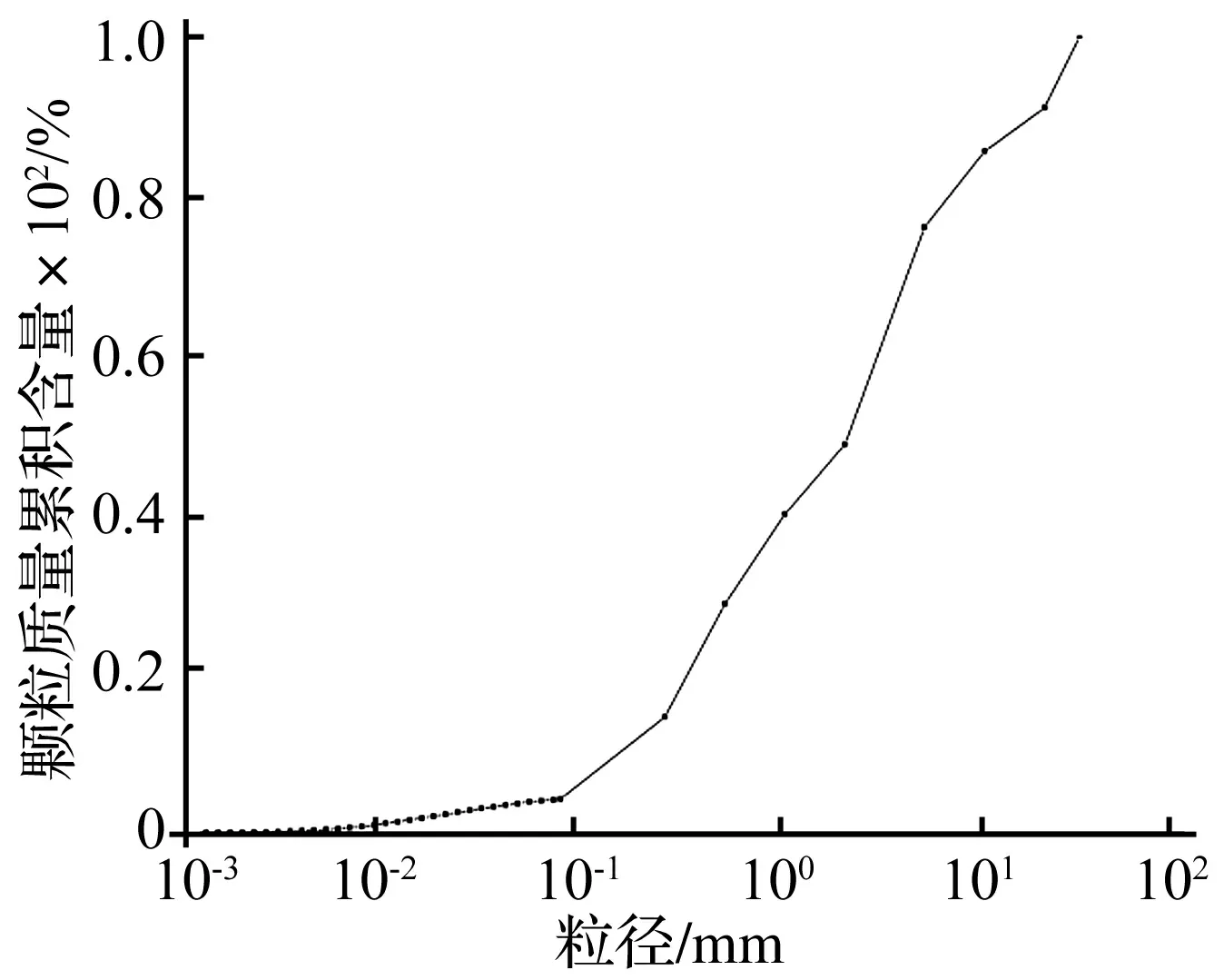
图1 土样级配曲线Fig.1 Grain-size distribution for the material

模型边坡高度0.6 m，为研究不同坡面角度条件下碎石土斜坡动力响应规律，试验模型坡面角度分别设计为35°，45°，55°；坡体内部布置与临空面等距剖面，埋设5个二向加速度传感器，用于测定水平向和竖直向的加速度响应值。台面固定一个2向加速度传感器，用于测定输入台面的加速度响应值。

模型斜坡制作方法，采用体积控制法，将材料分层压实至设计容重，每层压实厚度不超过5 cm，将传感器埋设置指定位置，2个传感器间距为0.14 m，压实完成后对斜坡坡面处理至指定坡度。

模型振动结束后，采用环刀取斜坡不同高程土样，测量在地震作用下碎石土容重随高程的变化规律。环刀尺寸为Φ70 mm×52 mm，容积为200 cm3，2个取样点间距为0.1 m(图2)。高清摄相机布置于坡肩位置，用于监测碎石土斜坡坡肩的运动过程；采用粒子图像测速法(PIV)分析地震作用下碎石土坡肩的动力响应特征。综上，结合碎石土坡体内部加速度响应规律，坡肩速度响应规律及动力破坏特征，揭示碎石土斜坡在地震作用下的变形破坏机制。

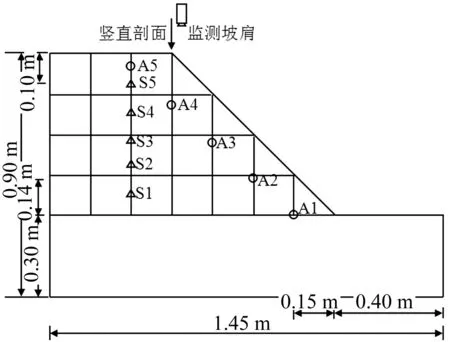
图2 监测方案布置(△采样点；○加速度测试点)Fig.2 Profile layouts of sensors in model slope (△sampling site；○acceleration test points)

2 斜坡的加速度动力响应规律

为了研究碎石土斜坡的加速度动力响应规律，在斜坡竖直剖面不同高程分别布设传感器，从下至上依次为A0、A1、A2、A3、A4和A5，A0在台面，测试台面的加速度动力响应特征；A1在坡脚，A5靠近坡顶，以分析斜坡内部加速度的高程放大效应。本文定义斜坡内任一点的加速度动力响应峰值与振动台面上加速度动力响应峰值的比值为加速度峰值放大系数。

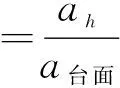
当PGA放大系数>1，斜坡内加速度动力响应比台面响应强烈，表现为加速度高程放大；当PGA放大系数<1，斜坡内加速度比台面响应弱，表现为加速度高程缩小。

2.1 水平向加速度响应规律

2.1.1 坡度的影响

以输入地震频率为25 Hz为例，斜坡内部水平向PGA放大系数随高程的变化规律如图3。试验结果表明，碎石土斜坡水平向加速度高程放大效应明显，PGA放大系数总体大于1，随高程的增加而增大。约以高程h/H=0.5为界，该高程以下PGA放大系数随高程的增大非常缓慢；该高程以上，PGA放大系数随高程的增大非常显著，由于坡顶处没有约束，PGA放大系数最大。

模型振动后，斜坡竖直剖面不同高程取土样测量土样容重，取样点从下至上依次为S1、S2、S3、S4和S5，测试结果如图4。不同高程土体容重随高程呈非线性减小趋势。约以高程h/H=0.6为界，高程以下，土体容重明显大于振动前斜坡土体容重；高程以上，土体容重明显小于振动前斜坡土体容重，坡顶土体容重最小，表明振动使碎石土斜坡内部出现明显的分层现象，以h/H=0.6为分界面，界面以下土体振动加密，界面以上土体振动变松，即振动过程中碎石土斜坡结构变为上松下紧，对于地震波的传播具有重要影响。坡体下部土体紧密，对水平向地震波的传播存在明显的抑制作用，水平向PGA放大系数随高程缓慢上升；当地震波通过分界面，到达上部松散土体，对水平向地震波传播的抑制作用降低，水平向PGA放大系数随高程快速上升(图3)。

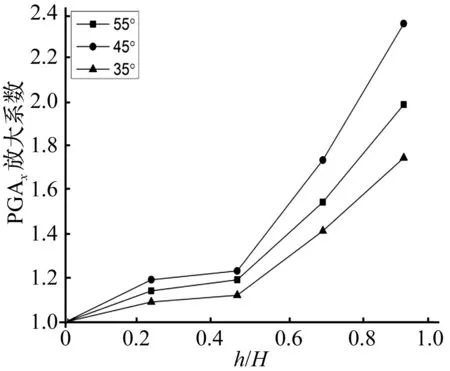
图3 不同坡角模型水平向加速度响应(25 Hz)Fig.3 Dynamic response of horizontal acceleration with different inclination angles (25 Hz)

地震波沿土体向上传播，由于土体和斜坡临空面的作用，坡体内部的加速度响应与台面输入的加速度响应不同[15]。为了研究坡面角度对峰值加速度高程放大效应的影响，选取坡面角度为35°，45°，55°。由图3可知，当频率为25 Hz时，随着坡面角度的增大，斜坡内部同一高程水平向峰值加速度放大效应为35°<55°<45°。即随着坡面角度的增大，水平向峰值加速度的高程放大效应出现逐渐增强的趋势，到达45°附近，水平向加速度峰值加速度的高程放大效应随坡度的增大，出现减弱趋势。综合考虑5个振动频率下，35°，45°，55°斜坡模型的振动响应特征， 45°坡体动力响应最明显。

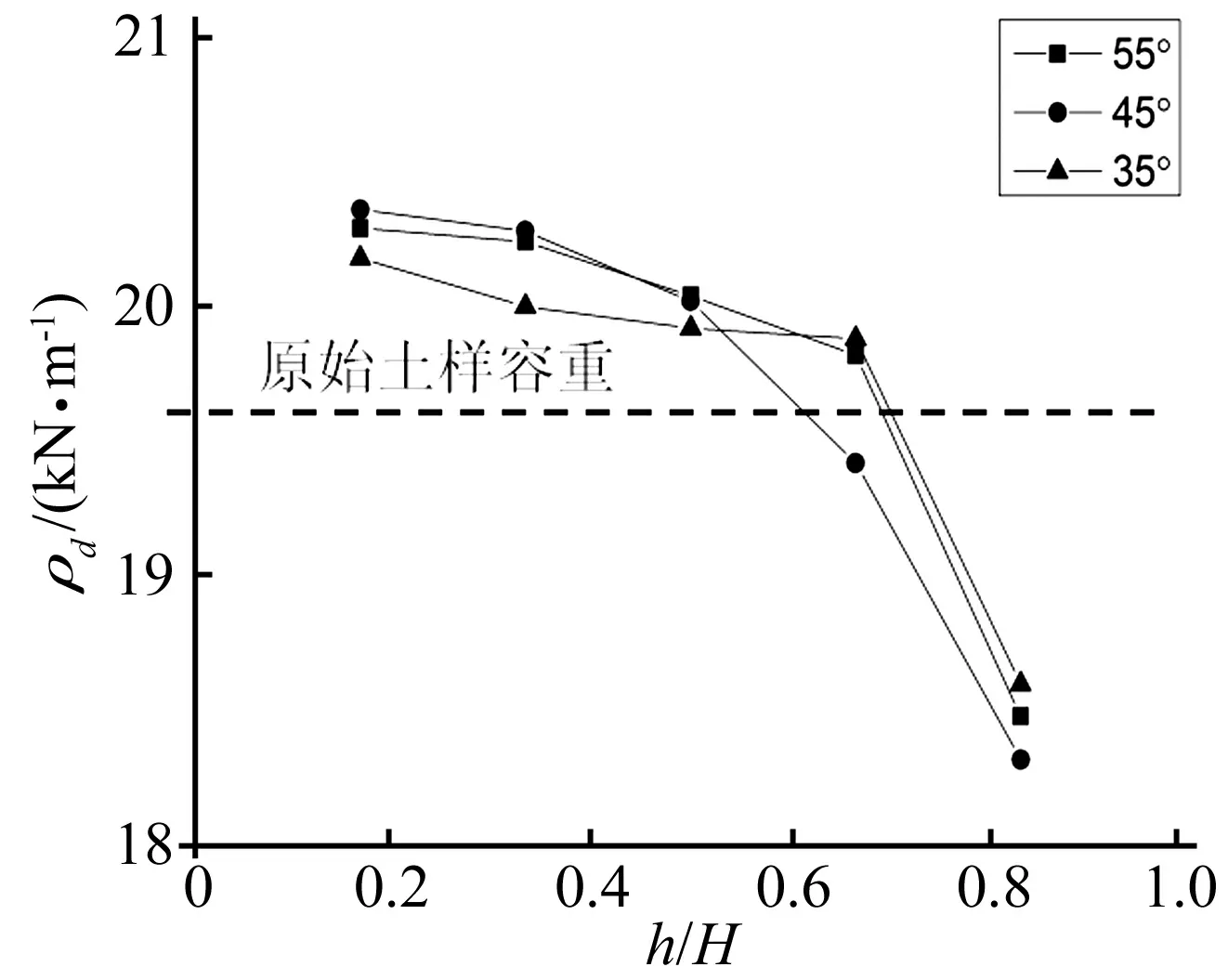
图4 振动后坡体容重的变化(25 Hz)Fig.4 The change of soil unit weight after vibration (25 Hz)

2.1.2 频率的影响

以坡面角度为45°为例，斜坡内部水平向PGA放大系数随高程的变化规律如图5。可以看出，输入不同频率的正弦波，碎石土斜坡内部水平向PGA放大系数随高程的增大，呈上升的趋势，在坡顶达到最大值。当频率小于25 Hz，h/H<0.3，水平向PGA放大系数随高程减小；此高程以上，PGA放大系数随高程呈上升趋势。当频率大于25 Hz，以h/H=0.6为界，高程以下，PGA放大系数随高程缓慢上升，高程以上PGA放大系数随高程快速上升。随着地震频率的增加，坡体内部同一高程水平向PGA放大系数逐渐增大，当输入频率为25 Hz，响应最强烈。

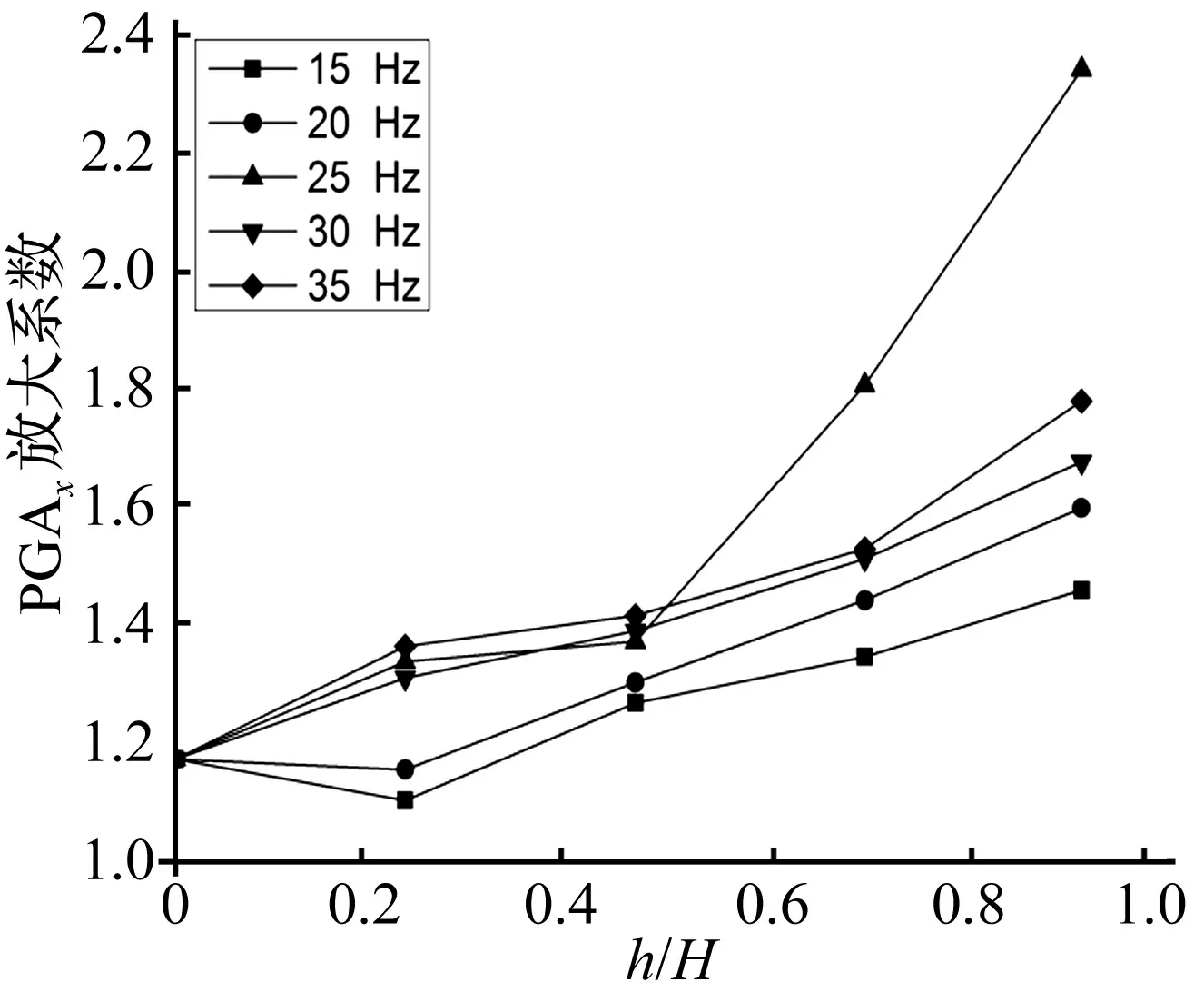
图5 不同振动频率作用下模型水平加速度响应(45°)Fig.5 Dynamic response of horizontal acceleration in different frequency(45°)

在地震动作用下，模型斜坡底部水平向加速度具有明显的局部缩小或缓慢上升的现象，表明由于振动及土体自重作用的影响，模型边坡底部土体压密，对地震波有一定的抑制作用，频率越小，抑制作用越明显。如图6，以h/H=0.6为界，界限以下土体发生振密现象，随着频率的增大，振动后土体容重增高；界限以上土体发生振松现象，随频率的增大，振动后土体容重越低；当频率为25 Hz附近时，无论是底部振密还是上部振松效果都是最显著的。

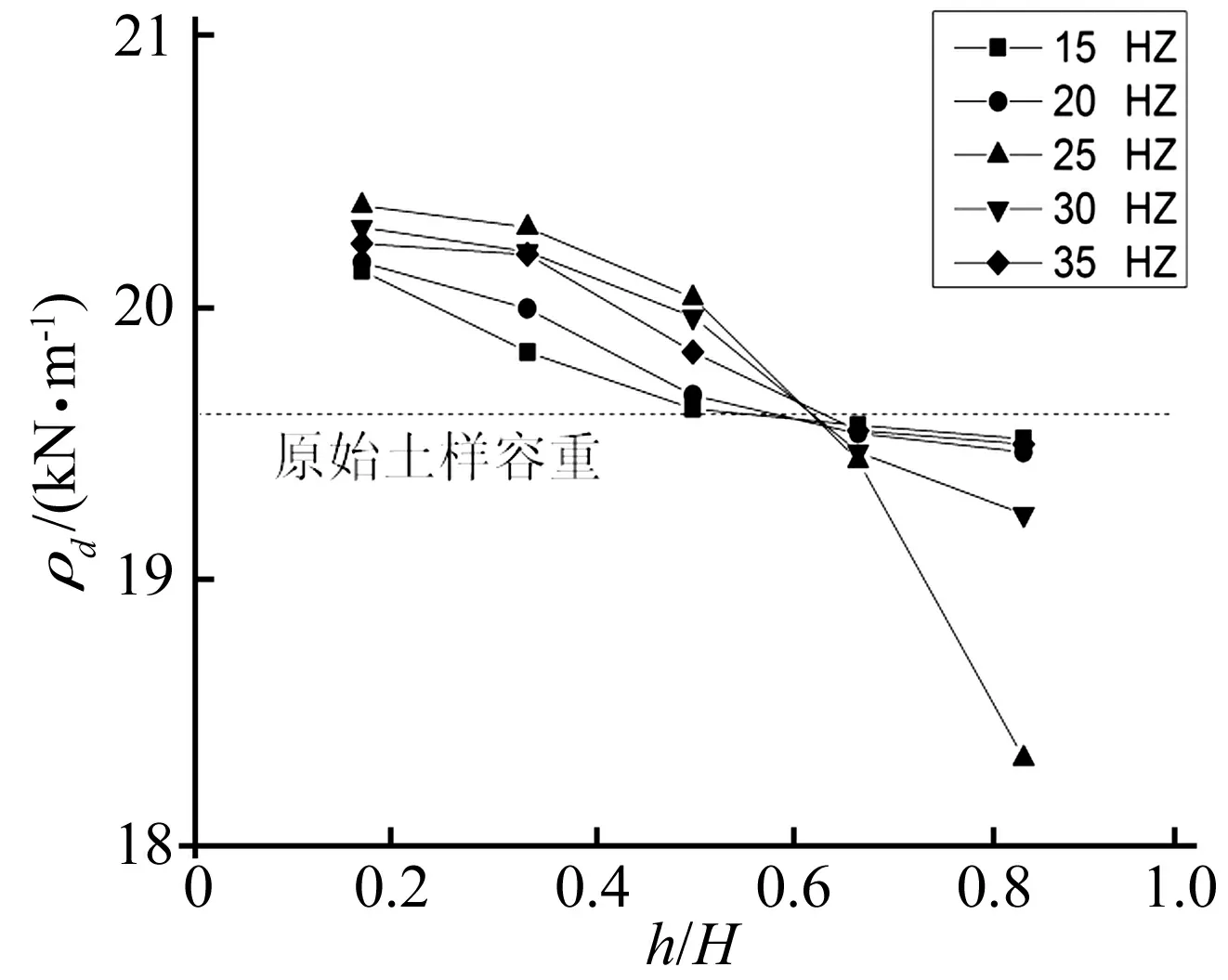
图6 振动后坡体容重的变化(45°)Fig.6 The change of soil unit weight after vibration (45°)

2.2 竖直加速度响应规律

以往研究地震对坡体动力响应的影响，主要集中于水平方向的地震动力作用，主要由于水平向地震力对坡体造成的破坏更严重。汶川地震后，众多学者认为强震区竖向加速度动力响应是造成斜坡破坏的重要因素[16]。

2.2.1 坡度的影响

以坡度为45°为例，从坡脚到坡顶各测点竖直向响应加速度峰值放大系数如图7。图7表明，斜坡竖直向加速度放大系数随高程的增加，具有明显的高程放大效应。

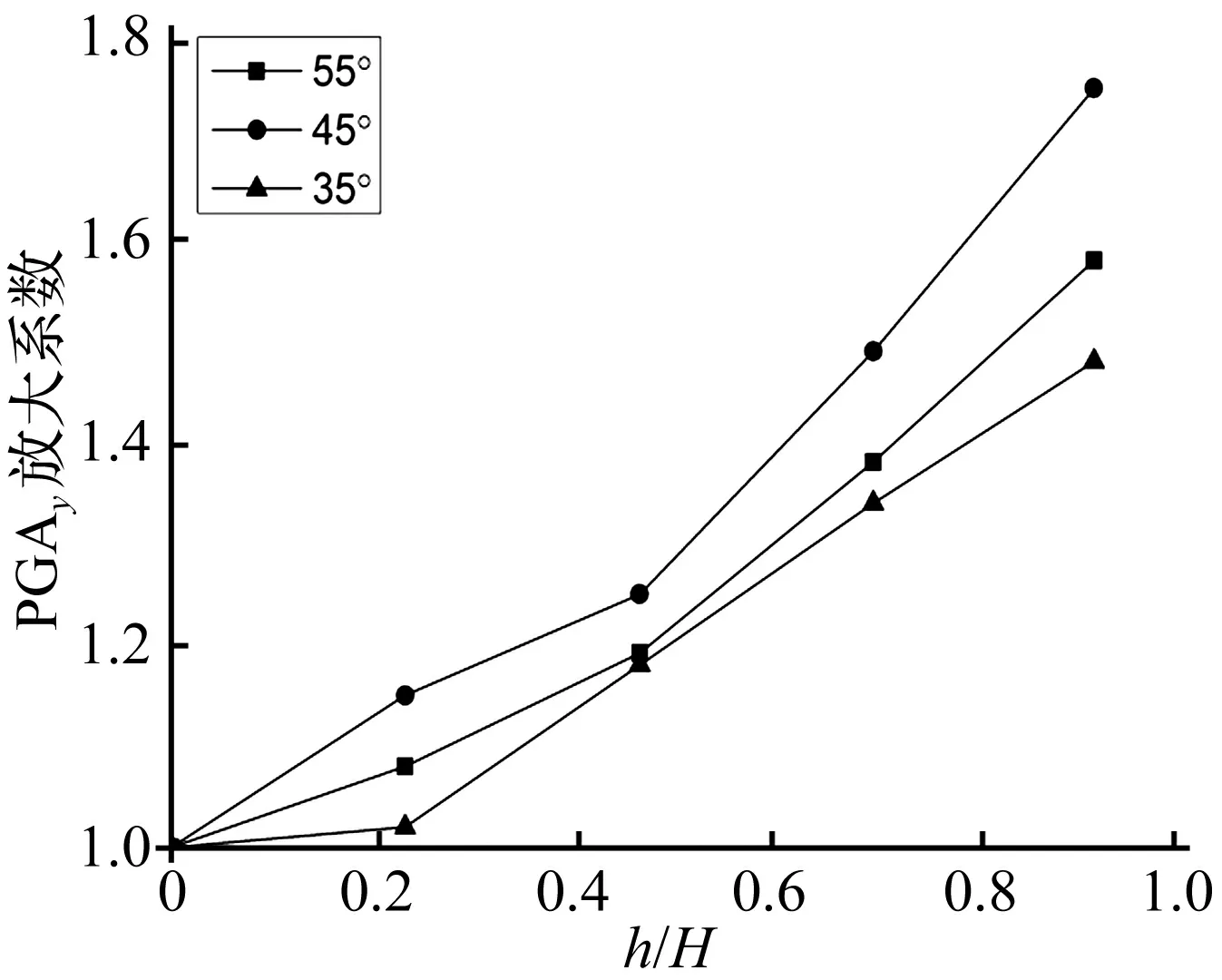
图7 不同坡角模型竖直向加速度动力响应(25 Hz)Fig.7 Dynamic response of vertical acceleration (25 Hz)with different inclination angles (25 Hz)

振动后斜坡土体容重随高程的变化规律表明振动使碎石土斜坡具有下紧上松的特征，竖向地震波传播方向为从“硬”土层进入“软”土层，由于软土层的强度低，在类似结构面的位置，发生的反射和折射现象弱。因此，斜坡竖向响应加速度的高程效应体现在整个高程内，不像水平加速度一样高程放大效应主要集中在斜坡中上部。斜坡内部同一高程竖直向响应加速度随坡度的增加呈先上升后下降趋势，与水平向响应加速度变化趋势一致，但小于水平向响应加速度峰值放大效应，主要由于竖直向重力的束缚作用。

2.2.2 频率的影响

从图8可以看出，不同频率的正弦波作用下，碎石土斜坡内部的竖直向加速度响应效果不同，PGA基本大于1.0，随着高程的增加，竖直向加速度增大，坡顶放大效应最强。随着振动频率的增大，斜坡内部同一高程竖直向PGA呈先上升后下降的趋势，25 Hz>20 Hz>15 Hz>30 Hz>35 Hz。实验现象也表明25 Hz时，模型竖直响应最明显，振动频率为35 Hz时，坡体动力响应效果较弱。

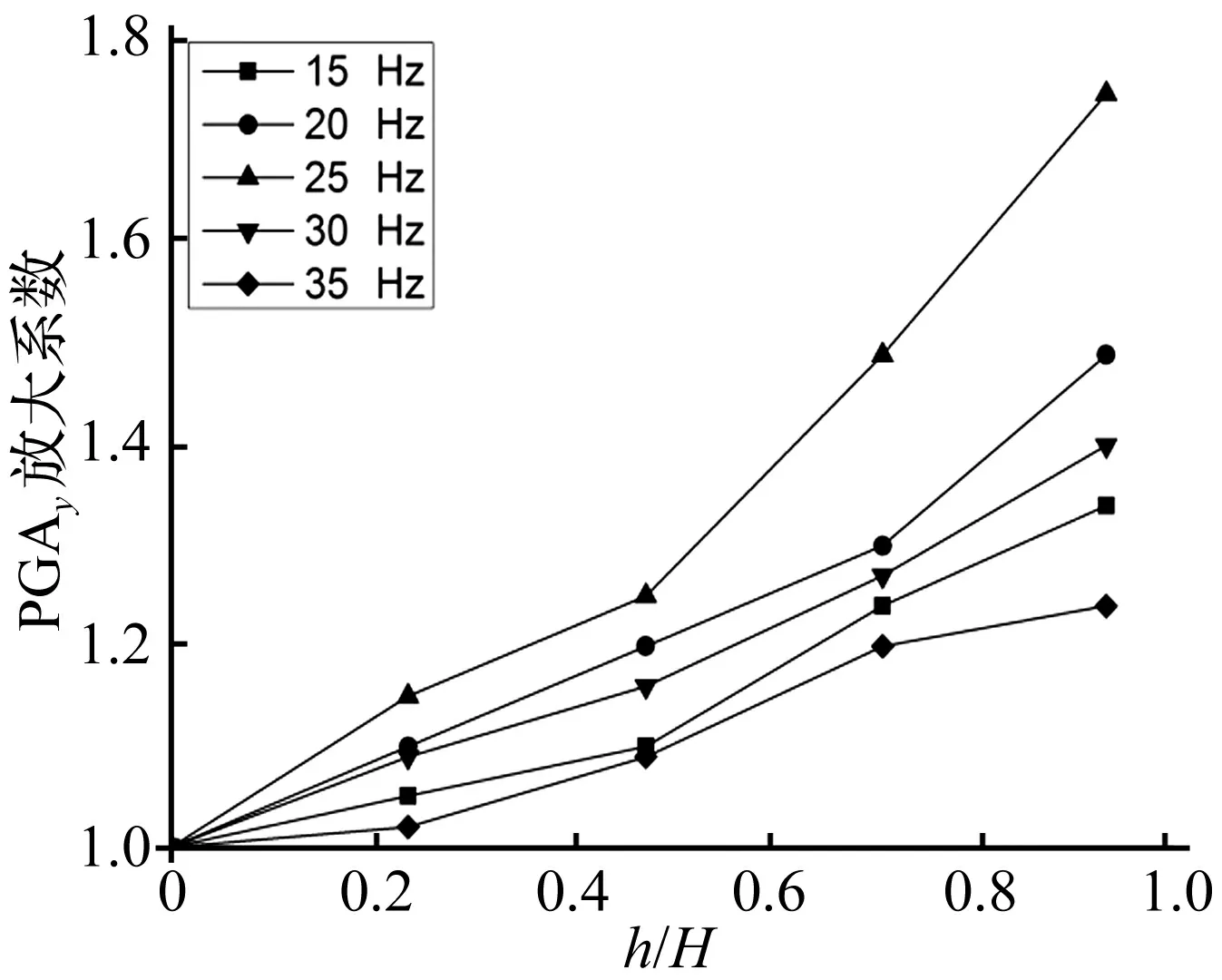
图8不同振动频率作用下模型竖直加速度响应(45°)Fig.8 Dynamic response of vertical acceleration in different frequency(45°)

振动后斜坡土体容重随高程的变化规律表明，振动使土质坡体出现分层效应，每层土体密实度不同，斜坡岩性和结构发生变化，影响了竖直向加速度响应规律。随着频率的增大，土坡的分层效应削弱了高频的竖直向地震波(图8)，出现了35 Hz高频地震波的竖直向动力响应低于其它频率的动力响应效果。

3 斜坡动力破坏特征

碎石土斜坡出现的破坏现象与斜坡动力加速度响应规律相一致。当频率为25 Hz，峰值0.2 g，持时20 s正弦波XZ双向激励下，斜坡模型首先发生坡肩破坏，坡顶产生大量拉裂缝；大量碎石土在振动作用下，脱离坡体，堆积于坡脚，坡体出现大规模沉降；坡体中上部土体松动，密实度降低，由于振动作用，坡顶表面产生大量散体状碎石(图9)。

斜坡变形破坏一般出现在振动轨迹的拐点，当运动速度由向坡体内部转为向临空时，降低了土地体的水平向约束强度，为斜坡水平运动创造条件。首先，由于竖直向的高程放大，产生了“上抛”运动的趋势，与水平向加速度高程放大效应共同作用，坡肩土体容易脱离整体，出现变形或破坏。

图9 模型变形破坏特征(55°，25 Hz)Fig.9 Characteristic of deformation and failure of model

图10为PIV分析结果表明，当频率为25 Hz时，斜坡坡肩的速度动力响应值为35°<55°<45°。当坡度为45°时，坡体的水平速度响应明显高于其它坡度，坡体晃动与破坏最明显。

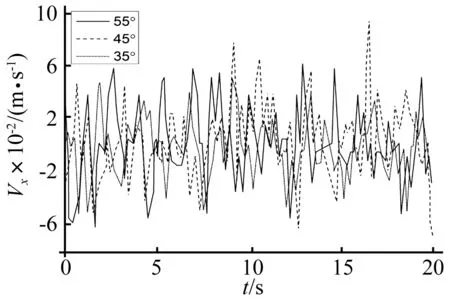
图10 不同坡度模型坡肩运动特征Fig.10 Movement characteristics of slope shoulder in different angle

图11表明，当坡度为45°时，坡肩的速度动力响应值为25 Hz>20 Hz>15 Hz>30 Hz>35 Hz。当频率为25 Hz，坡肩水平向速度响应最明显，坡体晃动强烈。PIV的分析结果与加速度高程放大效果分析的结果是一致的。

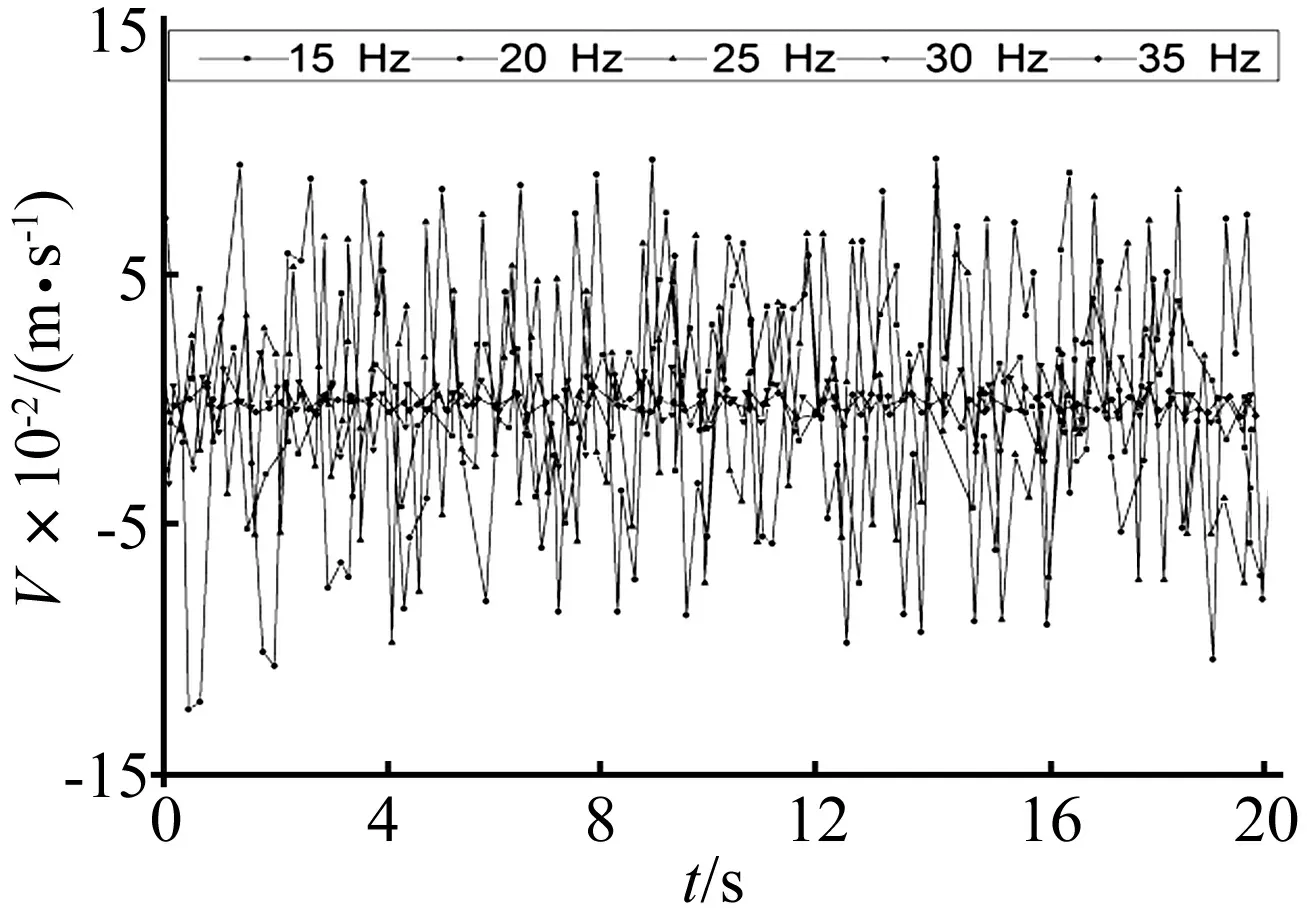
图11 不同频率模型坡肩运动特征Fig.11 Movement characteristic of slope shoulder in different frequency

4 结 论

本文设计并完成了1：100比尺的碎石土斜坡小型振动台模型试验，研究不同坡面角度，模型斜坡的动力响应规律与变形破坏特征，以及地震动参数对动力响应规律与变形破坏特征的影响。得到以下几点结论：

(1) 坡内水平加速度响应与竖直加速度响应具有相似的特征，均呈现出显著的高程放大效应，坡顶加速度放大效果明显，但竖直向加速度放大效应小于水平向响应加速度峰值放大效应。

(2) 35°、45°、55°三个坡度中，随着坡面角度的增加，坡内同一高程水平向或竖直向PGA放大系数呈先上升后下降趋势，坡面角度45°时，加速度高程放大效果最明显。水平向PGA放大系数随高程的变化趋势为坡体下部缓慢上升，坡体上部快速上升；竖直向PGA放大系数在整个高程范围内上升，无明显分界点。

(3) 坡面角度为45°时， 25 Hz水平向或竖直向加速度高程放大效果最明显。随着频率的增加，坡内同一高程水平向PGA放大系数呈上升趋势，小于25 Hz时，坡体下部水平向PGA放大系数缓慢下降，坡体中上部为快速上升；大于25 Hz时，坡体下部水平向PGA放大系数缓慢上升，坡体中上部为快速上升；随着频率的增加，坡体内同一高程竖直向PGA放大系数呈先上升后下降趋势，规律为25 Hz>20 Hz>15 Hz>30 Hz>35 Hz，竖直向PGA放大系数随着高程的增加，坡体内部竖直加速度上升。

(4) 碎石土斜坡首先发生坡肩破坏，坡顶产生大量拉裂缝，大量碎石土在振动作用下，脱离坡体，堆积于坡脚。PIV分析结果表明，当坡度为45°，频率为25 Hz时，坡肩水平向运动最剧烈，坡体晃动、破坏最明显。

[1] 李磊. 滑坡堆积体的地震波动力响应研究[D]. 成都: 成都理工, 2010.

[2] 张倬元, 王士天, 王兰生, 等. 工程地质分析原理[M]. 第3版.北京: 地质出版社, 2009.

[3] 周洪燕. 边坡地震响应及动力稳定性分析[D]. 成都: 西南交通大学, 2010.

[4] 王存玉. 地震条件下二滩水库岸坡稳定性分析[C]// 岩体工程地质问题(七). 北京:科学出版社,1987.

[5] 韩宜康, 杨长卫, 张建经, 等.坡面角度对岩质边坡加速度高程放大效应的影响[J]. 地震工程学报,2014,36(4): 874-880. HAN Yikang, YANG Changwei, ZHANG Jianjing, et al. The influence of slope angle on the elevation amplification effect of rock slope acceleration [J]. China Earthquake Engineering Journal, 2014, 36(4): 874-880.

[6] 许冲, 徐锡伟, 郑文俊,等. 2013年四川省芦山“4.20”7.0级强烈地震触发滑坡[J]. 地震地质, 2013, 25(3): 641-655. XU Chong, XU Xiwei, ZHENG Wenjun, et al. Study on the characteristics, mechanism and spatial distribution of Yushu Earthquake triggered landslides [J]. Seismology and Geology, 2012， 34(1): 47-62.

[7] 田颖颖, 许冲, 徐锡伟, 等. 2014年鲁甸MS 6.5 地震震前同震滑坡空间分布规律对比分析[J]. 地震地质, 2015, 37(1): 291-306. TIAN Yingying, XU Chong, XU Xiwei, et al. Spatial distribution analysis of coseismic and pre-earthquake landslides triggered by the 2014 Ludian Ms 2.5 earthquake[J]. Seismology and geology, 2015, 37(1):291-306.

[8] 丁彦慧．中国西部地区地震滑坡预测方法研究[D]. 北京：中国地质大学,1997.

[9] 祁生文, 伍法权. 边坡动力响应规律研究[J].中国科学E辑技术科学, 2003, 33(增刊1): 28-40. QI Shengwen, WU Faquan. Research on dynamic response laws of slope[J]. Science in China Ser.E Technological Scienscs, 2003, 33(Sup1): 28-40.

[10] 朱元清, 胡天跃, 郭自强. 地震波在粘弹介质中的传播及地形效应[J]. 地震学报, 1991, 13(4): 442-449. ZHU Yuanqing, HU Tianyue, GUO Ziqiang. Propagation of seismic waves in a viscoelastic medium and the effect of topography[J]. Acta Seismologica Sinica, 1991, 13(4): 442-449.

[11] 周红, 高孟潭, 俞言祥. SH波形效应特征的研究[J]. 地球物理学进展, 2010, 25(3): 775-782. ZHOU Hong, GAO Mengtan, YU Yanxiang. A study of topographical effect on SH waves[J]. Progress in Geophysics, 2010, 25(3): 775-782.

[12] 陈建君. 复杂山区斜坡的地震动力响应分析[D]. 成都: 成都理工大学, 2009.

[13] 许建聪, 尚岳全. 碎石土渗透特性对滑坡稳定性的影响[J]. 岩石力学与工程学报, 2006, 25(11): 2264-2271. XU Jiancong, SHANG Yuequan. Influence of permeability ofgravel soil on debris landslide stability[J]. Chinese Jounral of Rock Mechanics and Engineering, 2006, 25(11): 2264- 2271.

[14] 姚晓阳, 杨小永, 曾钱帮. 碎石土滑坡工程地质特性及防治方案研究[J]. 工程地质学报, 2012, 20(3): 369-377. YAO Xiaoyang, YANG Xiaoyong, ZENG Qianbang. Engineering geology characteristics and prevention measure of landslides in soil and rock debris slopes[J]. Journal of Engineering Geology, 2012,20(3): 369-377.

[15] 徐光兴, 姚令侃, 高召宁, 等. 边坡动力特性与动力响应的大型振动台模型试验研究[J]. 岩石力学与工程学报, 2008, 27(3): 624-632. XU Guangxing, YAO Lingkan, GAO Zhaoning, et al. Large scale shaking table model test study on dynamic characteristics and dynamic responses of slope[J]. Chinese Jounral of Rock Mechanics and Engineering, 2008, 27(3): 625-631.

[16] 许强, 刘汉香, 邹威, 等. 斜坡加速度动力响应特性的大型振动台试验研究[J].岩石力学与工程学报,2010,19(12): 2420-2428. XU Qiang, LIU Hanxiang, ZOU Wei, et al. Large-scale shaking table test study of acceleration dynamic responses characteristics of slopes[J]. Chinese Jounral of Rock Mechanics and Engineering, 2010,19(12): 2420-2428.

Dynamic response characteristics of gravel soil slope with different angles of inclination

LIANG Shuangqing1,4, SU Lijun1,2,3, WANG Yang1,4

(1. Key Laboratory of Mountain Hazards and Earth Surface Processes, Research Institute of Mountain Hazards and Environment, CAS, Chengdu 610041, China;2. State Key Laboratory of Architecture Science and Technology in West China, Xi’an University of Architecture and Technology, Xi’an 710055, China;3. CAS Center for Excellence in Tibetan Plateau Earth Sciences, Beijing 100101, China;4. Graduate School University of Chinese Academy of Sciences，Beijing 100049，China)

A small-scale shaking table test for gravel soilslope with the geometric scale of 1:100 and inclination angles of 35°，45°and 55°was designed. A series of tests were performed under the excitation of sine waves with different frequencies in X and Z directions. The laws of dynamic responses and the characteristics of deformation and failure for gravel soil slope were studied. Results showed that the elevation has an amplification effect on seismic waves; the amplification of horizontal peak acceleration is stronger than that of vertical peak acceleration: with increase in inclination angle, the peaks of horizontal and vertical accelerations increase firstly and then decrease, the most obvious amplification occurs during the inclination angle of 45°; with increase in elevation, the peak of horizontal acceleration increases slowly at the lower part of the slope, but it increases quickly at the upper part; the peak of vertical acceleration increases with in the whole elevation; with increase in frequency, the peak of horizontal acceleration at the same elevation level increases, and the peak of vertical acceleration increases firstly and then decreases; the most obvious elevation’s amplification effect occurs when the frequency is 25 Hz. The PIV analysis showed that the horizontal movement of slope shoulder is the most obvious during the inclination 45°and the frequency is 25 Hz. It was shown that the gravel soil slope is easy to have shoulder failures under earthquake action.

seismic; gravel soil slope; dynamic response; angles of inclination; deformation and failure

国家重点基础研究发展计划(973)课题(2013CB733201)；中科院重点部署项目(KZZD-EW-05-01)

2015-07-14 修改稿收到日期：2015-10-13

梁双庆 男，博士生，1983年8月生

苏立君 男，博士，研究员，1976年12月生

P642

A

10.13465/j.cnki.jvs.2016.21.024