双边肋桥梁断面软颤振非线性自激力模型

朱乐东， 高广中

(1.同济大学 土木工程防灾国家重点实验室，上海 200092； 2.同济大学 土木工程学院桥梁工程系， 上海 200092；3.同济大学 桥梁结构抗风技术交通行业重点实验室，上海 200092)



双边肋桥梁断面软颤振非线性自激力模型

朱乐东1,2,3， 高广中1,2

(1.同济大学 土木工程防灾国家重点实验室，上海 200092； 2.同济大学 土木工程学院桥梁工程系， 上海 200092；3.同济大学 桥梁结构抗风技术交通行业重点实验室，上海 200092)

采用弹簧悬挂节段模型测振的方法，研究了双边肋桥梁断面的软颤振响应。试验中观察到明显的软颤振现象，软颤振发生在扭转模态内，以单自由度的扭转振动为主，弯扭耦合效应比较微弱。将颤振导数拓展为瞬时扭转振幅的函数，以计入自激力的非线性效应。参数识别结果表明，自激力的非线性主要体现为气动阻尼的非线性效应，气动刚度的非线性较弱。通过对比软颤振响应的计算值和试验值，初步验证了该自激力模型和参数识别结果的可靠性。根据气动阻尼和结构阻尼随瞬时振幅的变化关系，对软颤振的机理进行了探讨。

双边肋断面；软颤振；非线性自激力模型；非线性气动阻尼；软颤振机理

对于现代化大跨度桥梁，颤振是最危险的一类风致振动现象，1940年美国旧Tacoma悬索桥的风毁事故就是颤振引起的。实际桥梁必须在设计阶段通过风洞试验严格检验，并采取气动措施以消除颤振发生的可能性[1-2]。目前，桥梁颤振理论是以SCANLAN[3]在20世纪70年代建立的线性自激力模型为基础的，该理论只考虑颤振自激力的线性项，当风速超过一个临界点，即颤振临界风速时，线性气动负阻尼大于结构阻尼，桥梁断面的振幅随风速呈指数增加而出现颤振发散，因此，经典的线性理论将桥梁颤振视为线性气动失稳现象，在数学上简化为复特征值问题[2]。然而，SCANLAN的线性自激力模型只有在微幅振动条件下才是适用的，由于桥梁断面的非流线型气动外形，任何有限振幅的振动使得气动外形伴随着攻角的变化而改变，在此过程中自激力不可避免地表现出非线性特性。

近年来，桥梁断面在大振幅状态下的自激力非线性效应是风工程领域研究的一个热点。一些学者尝试建立了能够考虑自激力非线性效应的数学模型，例如徐旭等[4-5]提出的考虑主梁断面三个运动完全耦合的非线性准定常模型，其模型的线性部分与SCANLAN的线性模型一致，而非线性部分比较复杂，需要根据具体情况进行推导；张朝贵等[6]采用范德波尔自激振荡方程来模拟软颤振现象，用范德波尔非线性阻尼模型来模拟气动阻尼力的非线性效应；刘十一等[7-8]通过引入若干与流场特性有关的状态变量，建立了考虑自激力非线性效应的状态空间模型；WU等[9]提出了非线性自激力的Volteria卷积模型；NPRSTEK等[10-12]则提出了范德波尔-达芬类型的两自由度耦合的非线性自激力模型；DIANA等[13-14]提出非线性准定常自激力模型，并引入流变单元(rheologic element)来计入非定常效应；王骑等[15]建立了基于泰勒级数展开的非线性自激力模型。上述的非线性自激力模型虽然都具有一定的合理性，但并没有经过风洞试验充分验证，而且有些模型的数学形式过于复杂，因而，目前仍没有一个被普遍接受的非线性自激力模型。

国内外研究者在风洞试验中发现[6,16-19]，一些钝体桥梁断面或者流线型断面在大攻角姿态下，当线性气动负阻尼大于结构阻尼时，并不会出现线性理论所预测的发散性颤振即“硬颤振”，而是由于自激力的非线性效应稳定到一个有限振幅，即出现非线性的“软颤振”现象，经典的线性颤振理论对软颤振是不适用的。事实上，旧Tacoma桥的破坏过程也不是经典线性颤振理论所预测的振幅呈指数增加而瞬间破坏，而是经历了近70 min的大振幅反对称扭转振动，直至1/4 跨处扭转振幅达到约35°后，因吊索被逐根拉断而坍塌的[2]，在整个过程中表现出了非线性软颤振的特征。

由于具有显著钝体气动外形，扁平双边肋断面是桥梁工程中容易发生软颤振的典型断面型式，本文以该类断面的软颤振风洞试验现象为切入点，研究自激力在大振幅状态下的非线性特性，尝试提出非线性自激力模型，并初步探讨软颤振的发生机理。

1 软颤振风洞试验

双边肋断面的软颤振试验在同济大学TJ-2边界层风洞中进行，采用弹簧悬挂节段模型测振的试验方法，如图1所示，节段模型被放置在专门设计的内支架隔离墙中间，弹簧、吊臂、阻尼器和激光位移传感器等附属构件则位于隔离墙内部，以尽量保证二维流场并减少流动干扰。节段模型长约1.678 m，断面尺寸如图2所示。总质量约为19.198 kg，零风速时竖弯振动频率为1.520 Hz，扭转振动频率为2.661 Hz。所有试验均在均匀流场中进行。

图1 双边肋断面的弹簧悬挂节段模型Fig.1 Spring-suspended sectional model of a twin-side-girder section

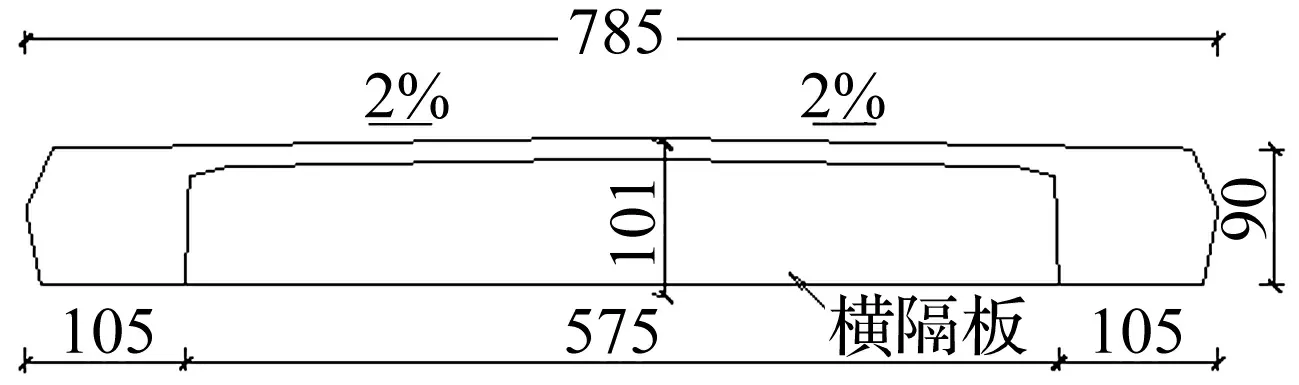
图2 双边肋断面(mm)Fig.2 Twin-side-girder section (mm)

当模型采用施工状态的裸断面，即未附加栏杆、护栏或检修轨道等附属设施时，软颤振振幅随约化风速的变化关系见图3，图3中试验均未附加阻尼器。从中可以发现：节段模型在3°和0°风攻角姿态下均出现了明显的软颤振，即当风速超过软颤振起振风速时，由于颤振自激力的非线性效应，模型并不会出现Scanlan线性模型所预测的振幅呈指数无限增大，而是稳定到一个有限振幅，该自限幅现象进一步显示在图4中，可以发现不论是从静止状态还是从大振幅激励状态开始，模型总能发展为一个稳定振幅(grow to stable amplitude, GTS; decrease to stable amplitude, DTS)，软颤振的稳定振幅随着约化风速的增加而近似线性地增加，当软颤振振幅增大到超过弹簧线性范围或激光位移传感器线性测试区间时，仍然未观察到发散性振动；对比3°和0°风攻角的振幅响应曲线可知，具有较钝气动外形的3°攻角姿态下的软颤振振幅增加更加缓慢、风速区间也更宽，因而，气动外形越钝对应的软颤振响应也就越显著。当风攻角为-3°时，自激力的非线性效应比较弱，当约化风速U*=2.0～2.8时，出现了软颤振现象，但当约化风速U*=2.8～3.91时，自激力的非线性不足以使颤振振幅稳定到一个固定振幅，而是出现了介于硬颤振和软颤振之间的非线性振动现象，即某个特定约化风速下随着激励振幅大小的不同存在多个稳定振幅，图3中标有向上箭头的数据点表示稳定振幅还可能进一步增大，而标有向下箭头的数据点则表示稳定振幅可能进一步减小，这种多个稳定状态的现象如图5所示，当约化风速U*>3.91时，出现了发散性振动，但由于自激力的非线性效应，振幅的增大过程要缓慢得多。

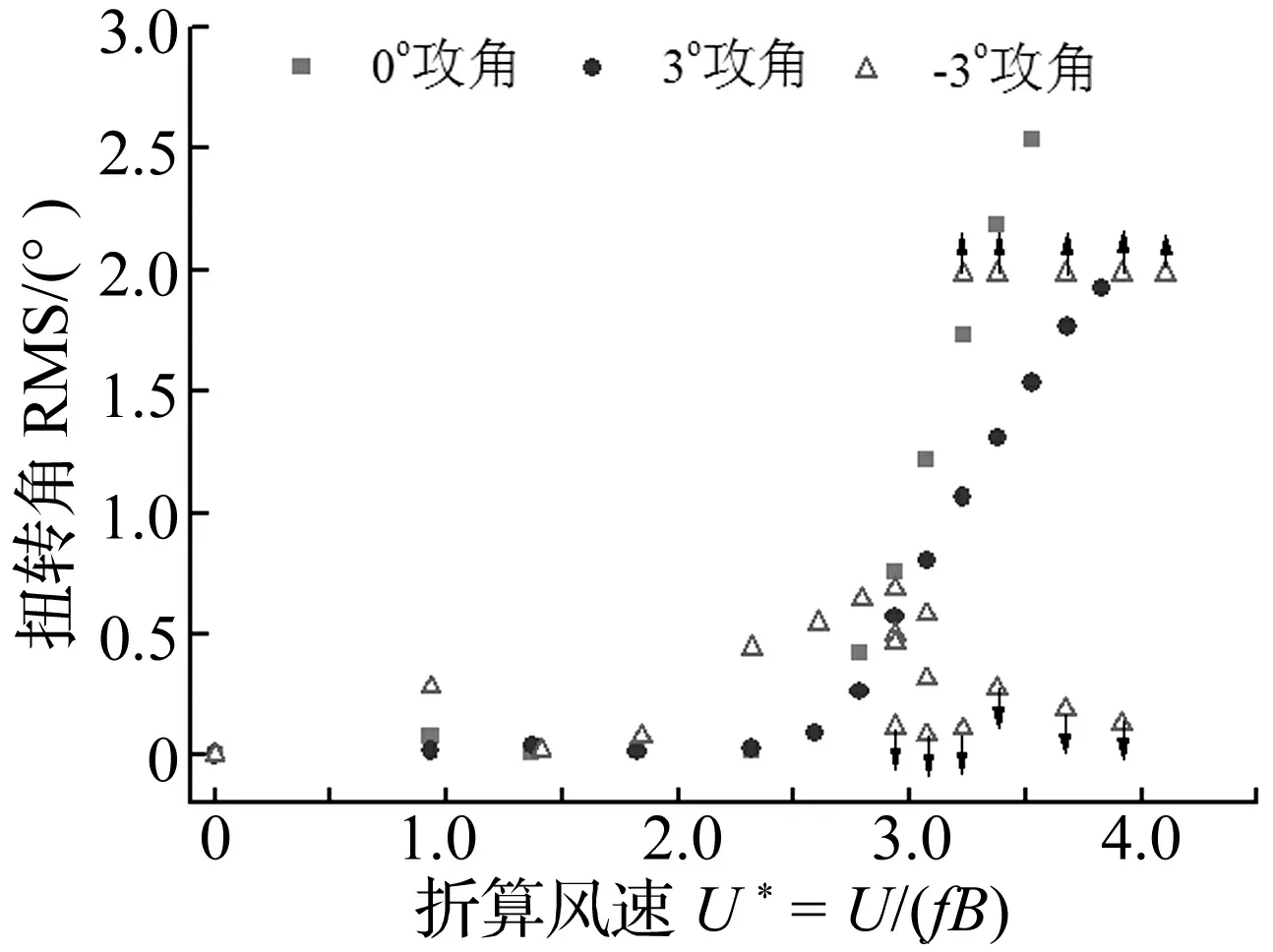
图3 软颤振振幅随约化风速变化关系(ξs=0.075%～0.1%)Fig.3 Relation between stable amplitude of soft flutter and reduced wind speed (ξs=0.075%～0.1%)

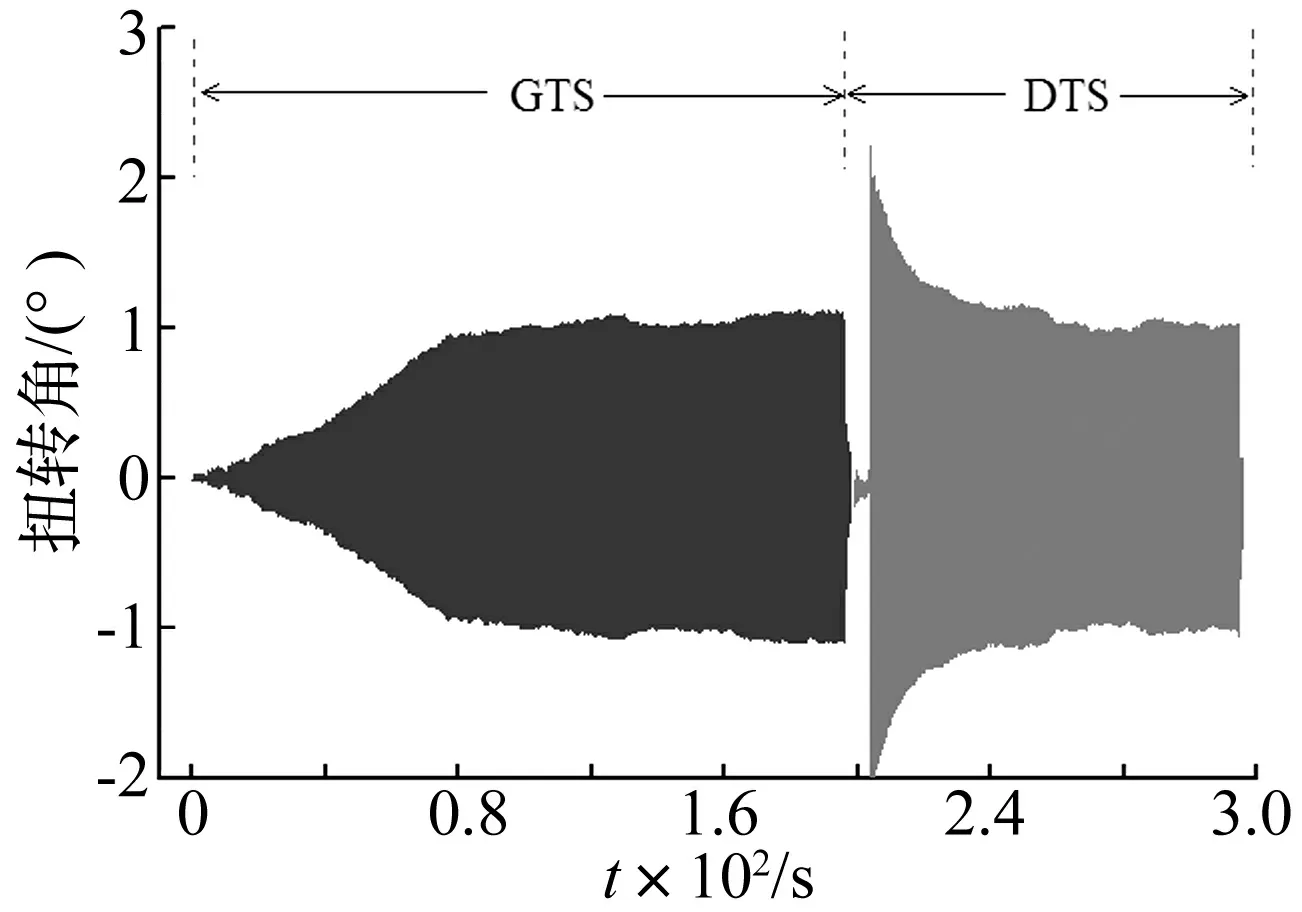
图4 软颤振自限幅振动现象(0°攻角，U*=2.935)Fig.4 Typical phenomenon of limit cycle oscillation (LCO) of soft flutter (attack angle 0°, U*=2.935 )

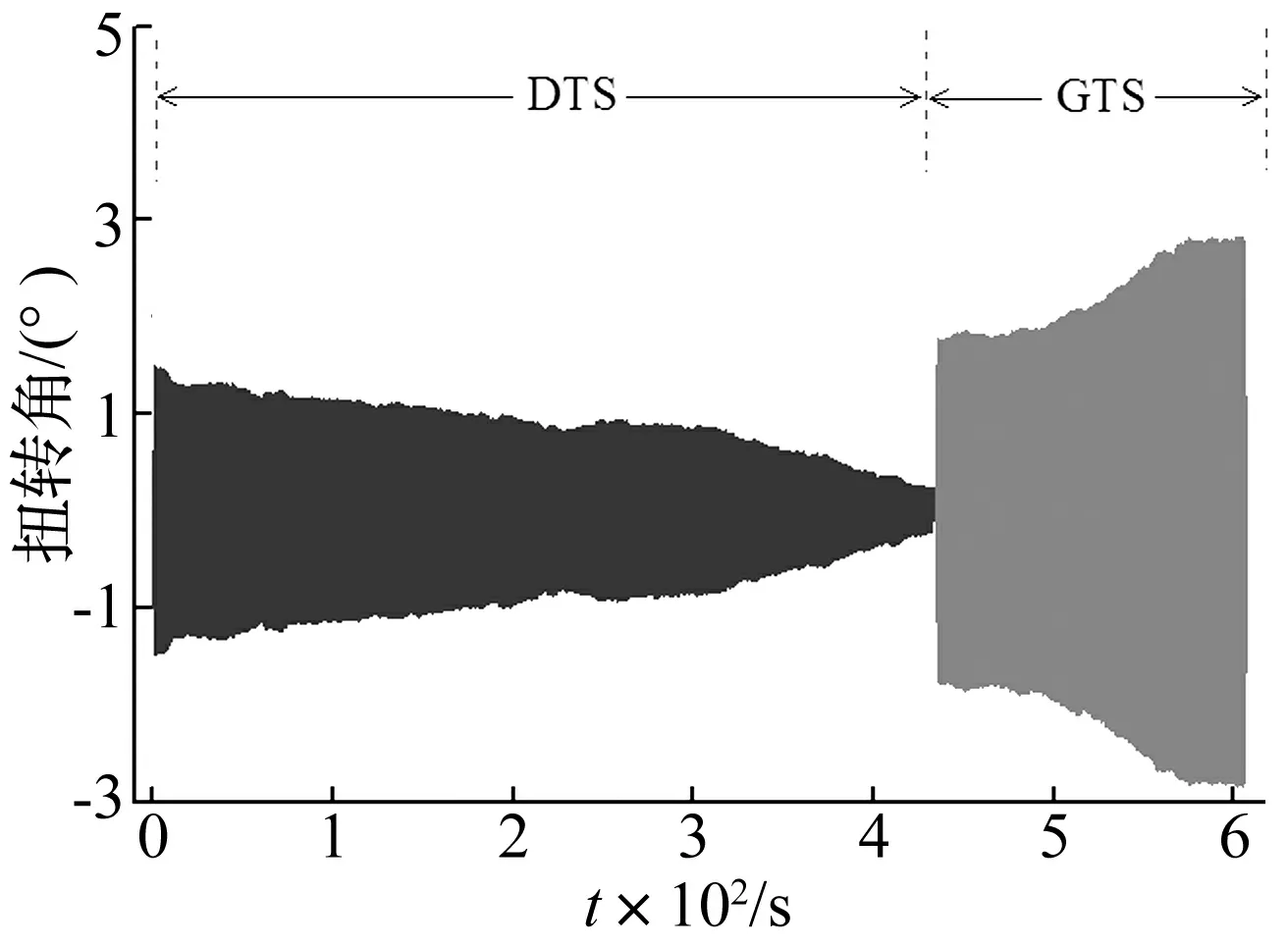
图5 稳定振幅依赖于激励大小的现象(-3°攻角，U*=3.229)Fig.5 Existence of multiple stable amplitudes under differentamplitude of excitation (attack angle -3°, U*=3.229)

在颤振振动形态方面，软颤振与经典的发散性硬颤振类似，软颤振是发生在单一扭转模态内的非线性振动，气动刚度中心作用点向上游移动，使得颤振时的扭转模态耦合了竖弯自由度，但弯扭耦合程度随着断面流线型程度的不同而差别很大，对于双边肋这类钝体断面，弯扭自由度耦合效应是极其微弱的，因而，该断面的软颤振可近似地视为单自由度扭转软颤振[16]。另外，施加栏杆、护栏或检修轨道等附属设施会进一步促进断面周围流场的分离，从而使成桥状态的软颤振响应更加显著[16]。为了讨论的方便，下文将讨论的范围限在施工状态。

2 软颤振非线性自激力模型及参数识别

2.1 非线性自激力模型

上节的风洞试验结果表明，由于大振幅状态下自激力的非线性效应，气动阻尼比不仅跟桥梁断面的气动外形有关，而且随着振幅的变化而改变，例如图4和图5中的系统阻尼依赖于激励振幅的大小。因而，在非线性自激力建模时，需要考虑振幅对气动参数的影响。另外，双边肋断面发生软颤振时，竖弯自由度的耦合效应比较微弱，其软颤振控制方程可近似简化为如下扭转振动方程：

(1)

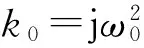
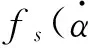
(2)

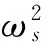
(3)

由式(2)可得到如式(4)所示的考虑了瞬时振幅ρ修正的非线性自激力模型。将该自激力模型表示成经典的形式：

(4)

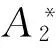
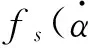
2.2 非线性参数识别

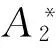
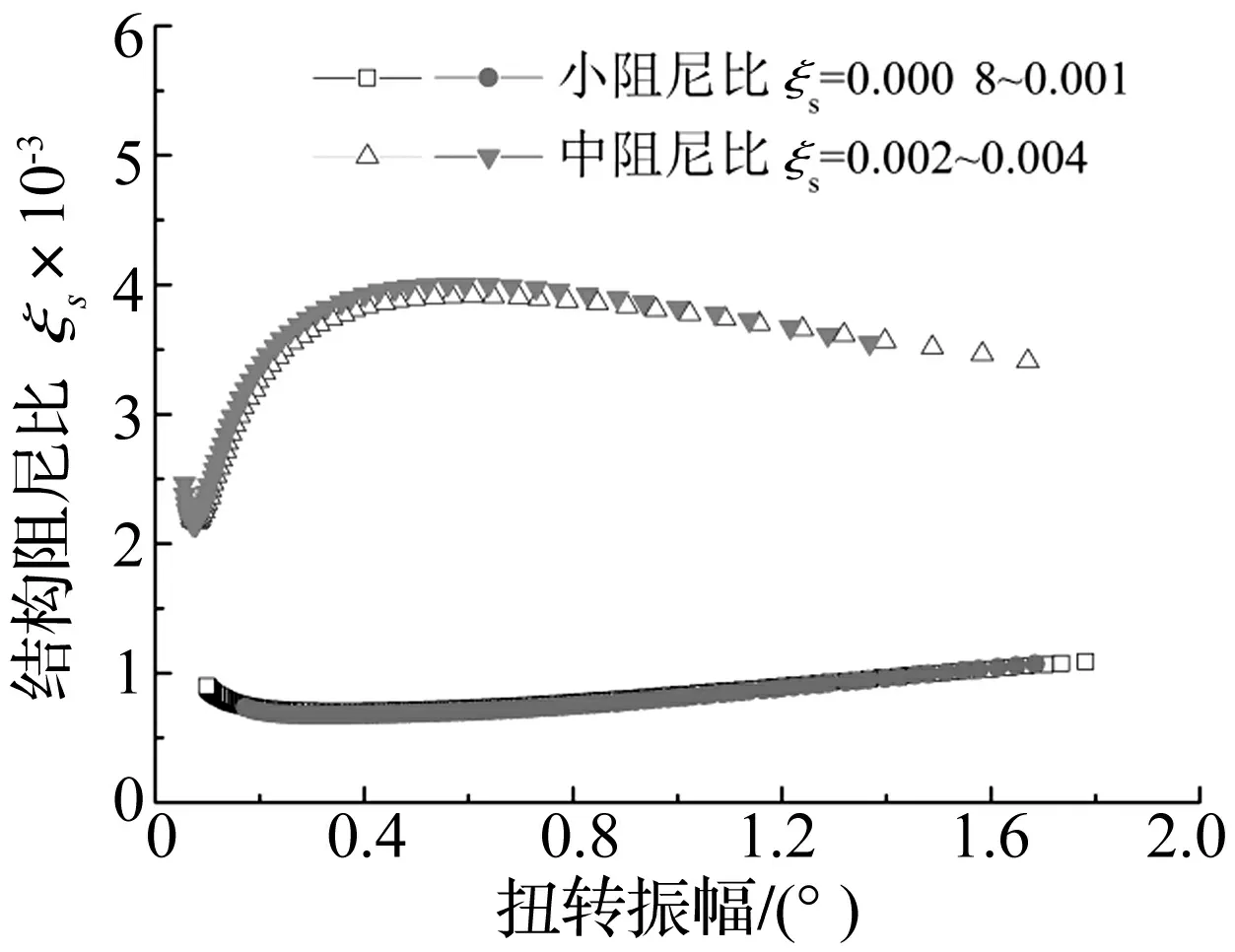
图6 非线性结构阻尼比ξs(ρ)(3°风攻角)Fig.6 Nonlinear structural damping ratio ξs(ρ) (attack angle 3°)

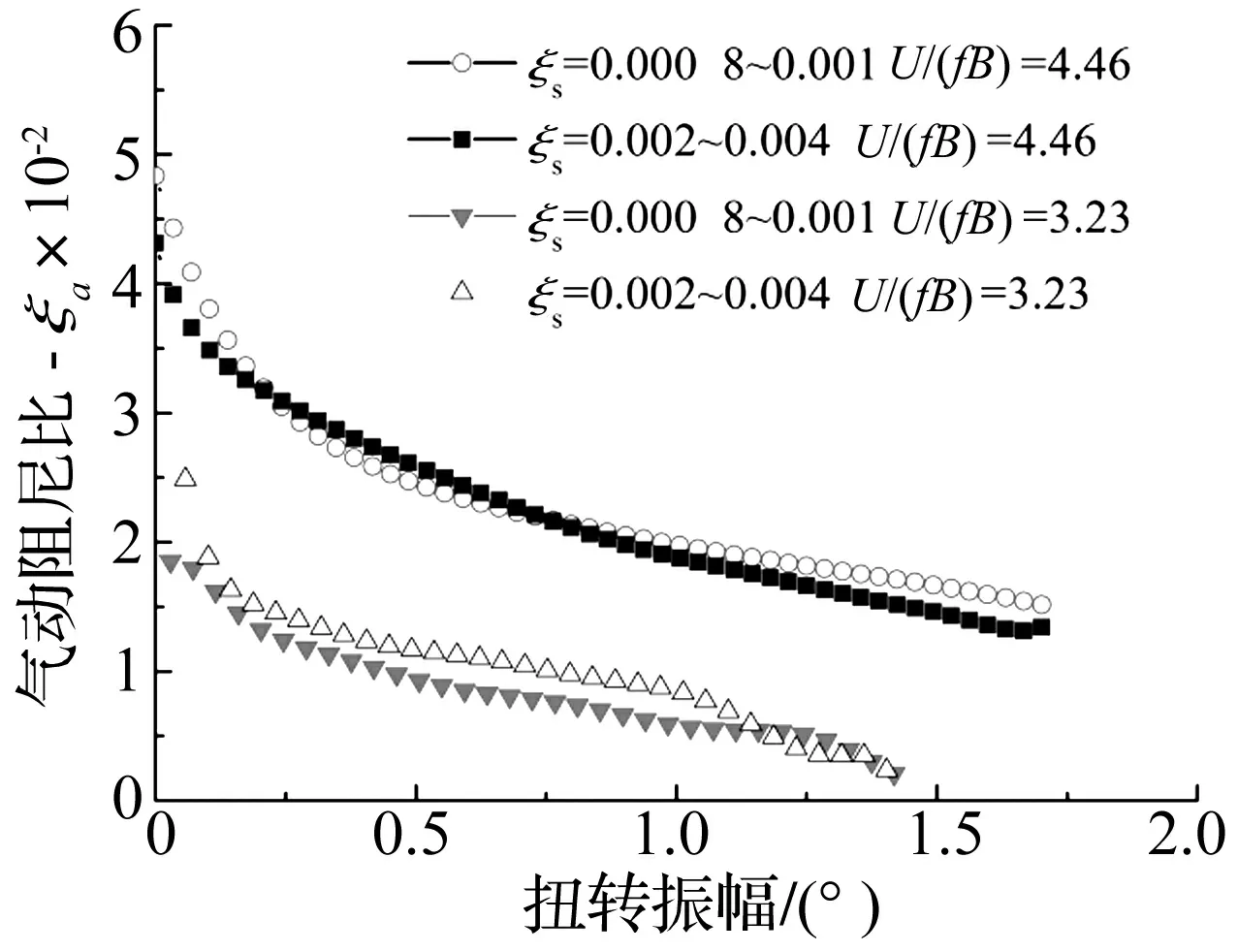
图7 非线性气动参数(ρ)(3°风攻角)Fig.7 Nonlinear aerodynamic damping parameter (ρ) (attack angle 3°)

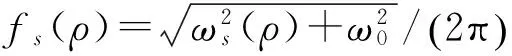
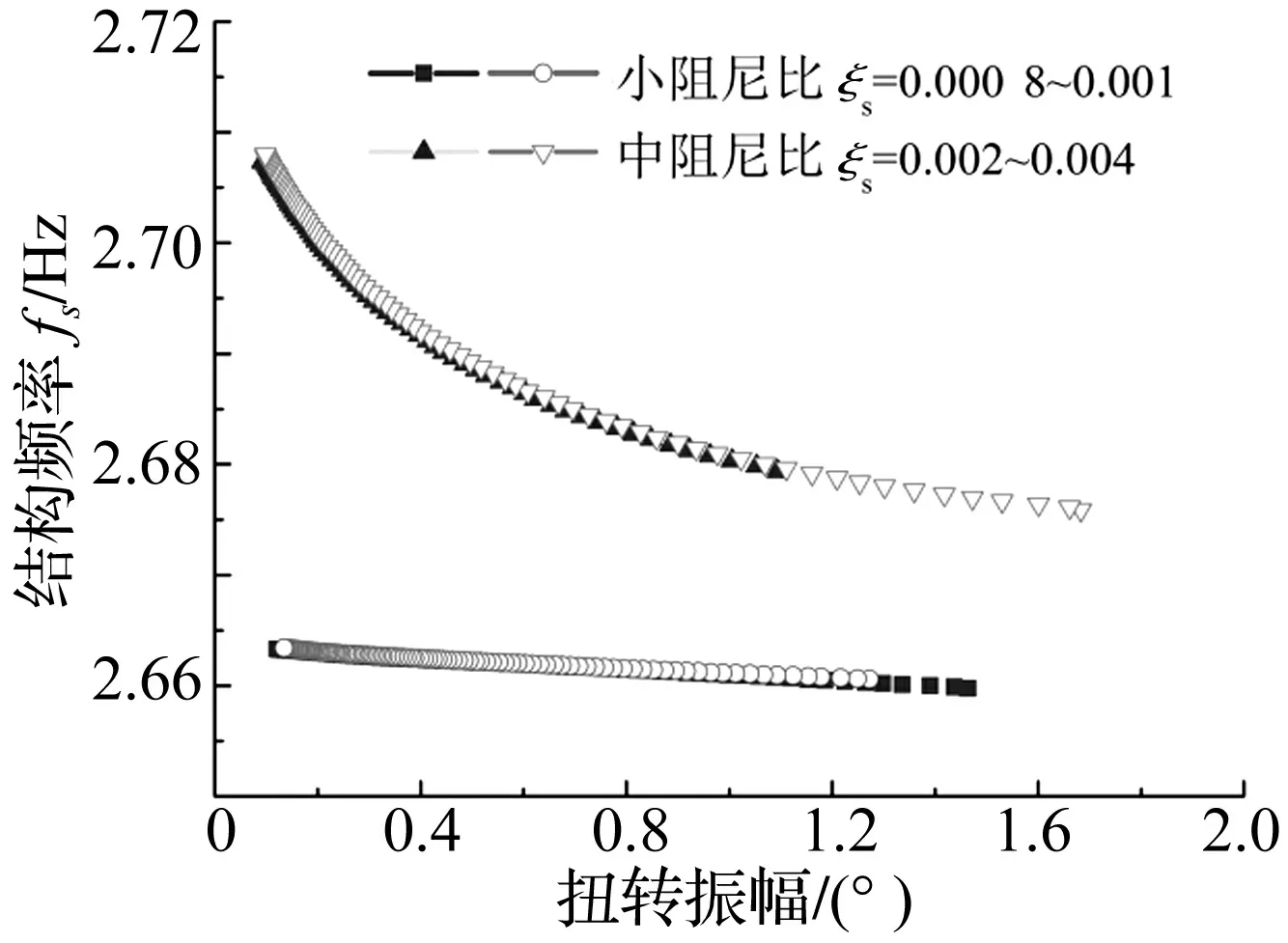
图8 非线性结构频率fs(ρ)(3°攻角)Fig.8 Nonlinear structural frequency fs(ρ) (attack angle 3°)

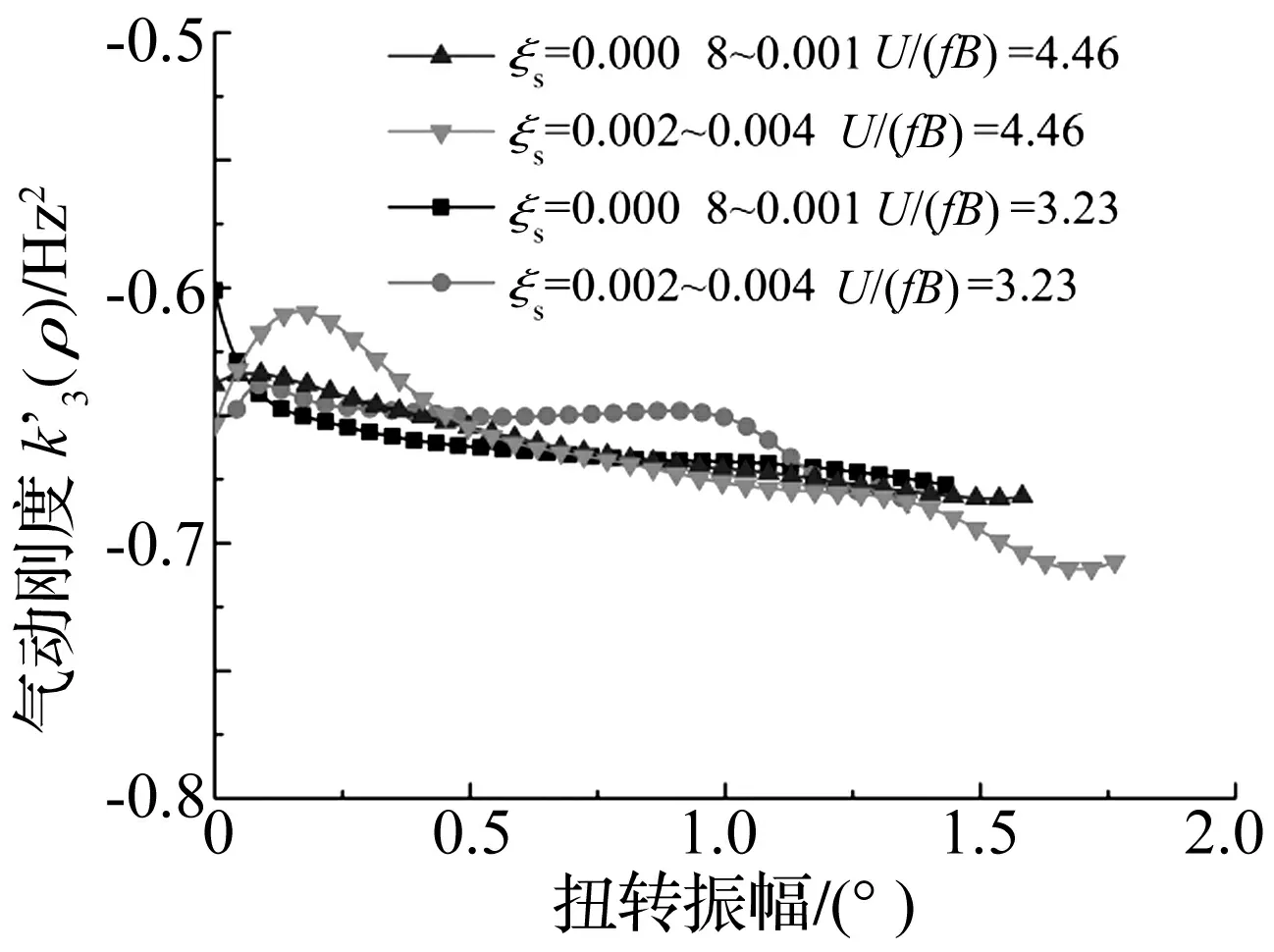
图9 非线性气动刚度参数(ρ)(3°攻角)Fig.9 Nonlinear aerodynamic stiffness parameter (ρ) (attack angle 3°)

2.3 试验验证

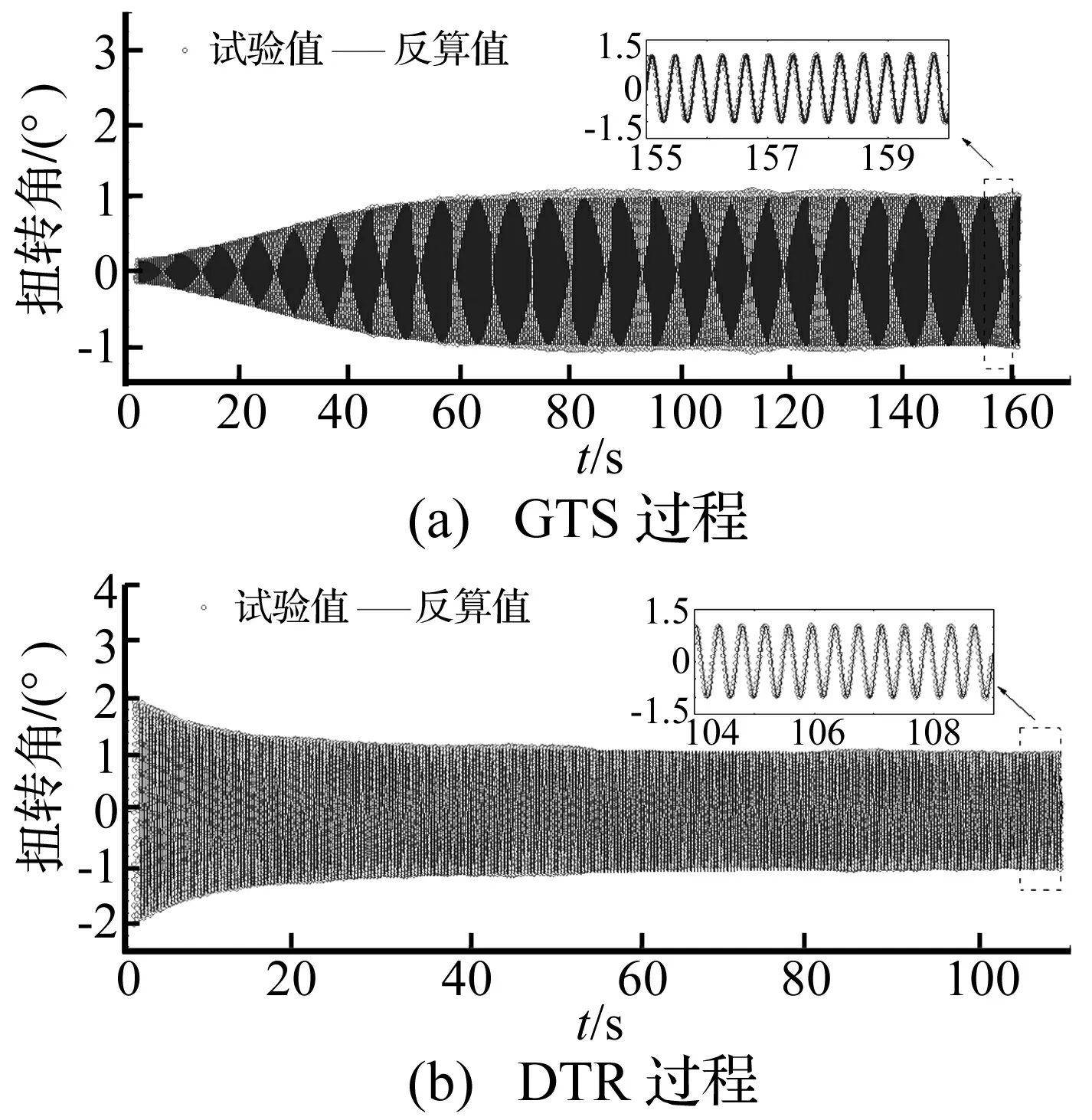
图10 软颤振响应的反算值与试验值对比(0°攻角, ξs=0.073%～1%, U*=2.94)Fig.10 Comparison of calculated soft flutter responses with test results (attack angle 0°, ξs=0.073%～0.1%, U*=2.94)

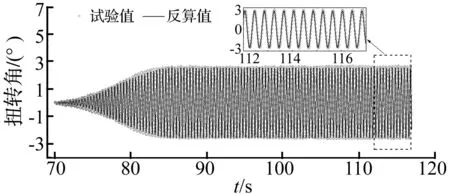
图11 软颤振响应反算值与试验值对比(3°攻角, ξs=0.2%～0.4%, U*=4.46)Fig.11 Comparison of calculated soft flutter responses with test results (attack angle 0°, ξs=0.2%～0.4%, U*=4.46)

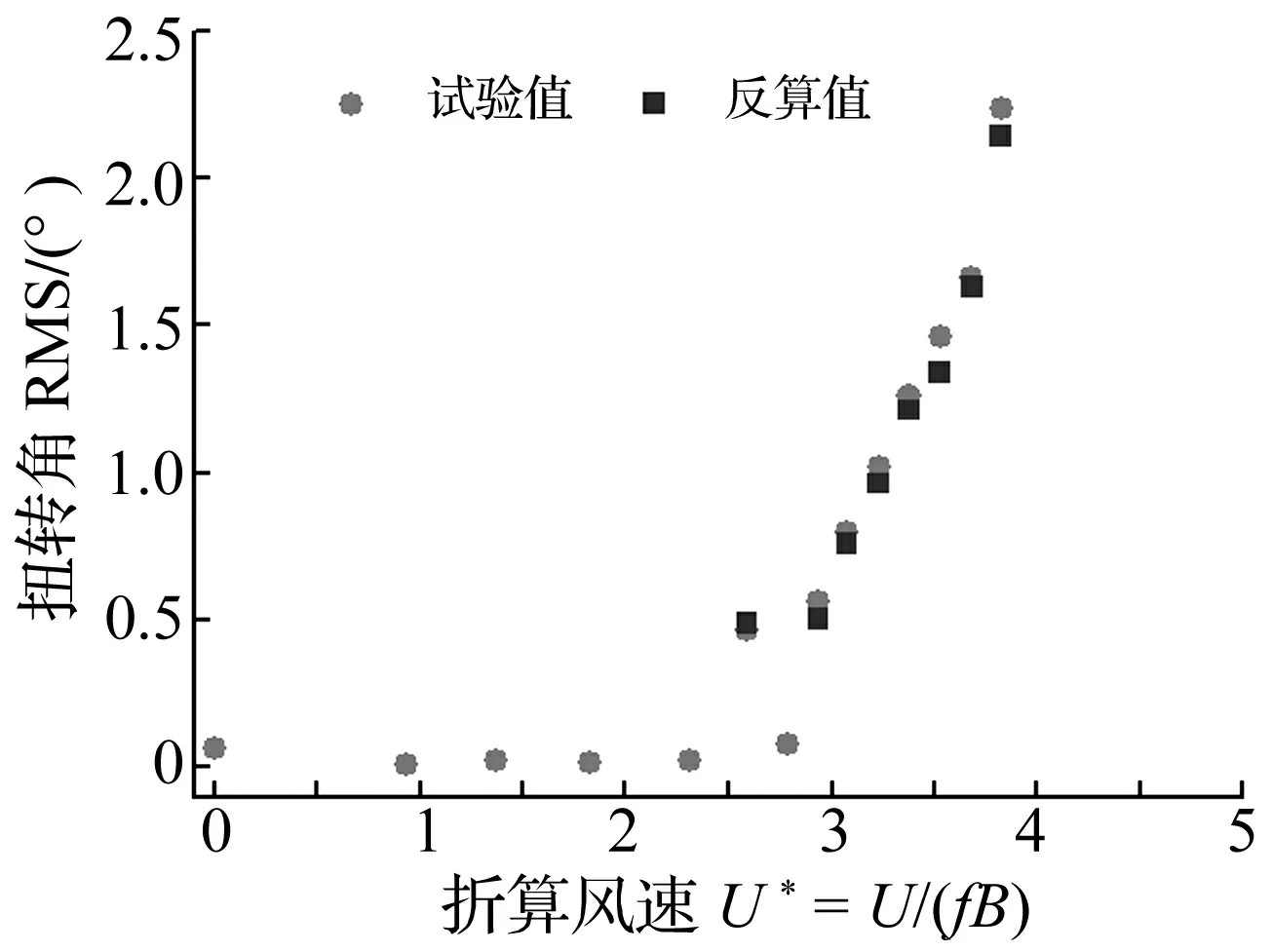
图12 软颤振扭转稳定振幅的RMS值反算结果与试验值对比(3°攻角, ξs=0.2%～0.4%)Fig.12 Comparison of calculated RMS of tosional amplitudes with experimental results (attack angle 3°, ξs=0.2%～0.4%)

3 软颤振的机理探讨

软颤振机理的讨论可以从结构阻尼比ξs(ρ)曲线和气动阻尼比ξa(ρ)曲线的相互关系入手。在探讨机理之前，需要首先得到ξs(ρ)和ξa(ρ)随振幅ρ变化的总体趋势。从图6中ξs(ρ)的识别结果可知，节段模型未加阻尼器时ξs随振幅ρ近似线性地缓慢增大，而附加了阻尼器之后，ξs(ρ)的曲线形状比较复杂，与阻尼器的类型和阻尼器的非线性特性有关，附加了钢丝圈阻尼器的ξs(ρ)在大振幅下近似线性地缓慢降低。为了研究非线性气动阻尼比ξa(ρ)随振幅和折算风速的变化趋势，在图13中给出了节段模型在3°攻角和4种约化风速U*的ξa(ρ)曲线，从中可以发现，ξa(ρ)曲线随着U*的增加逐渐向上抬升，而斜率则不断降低。

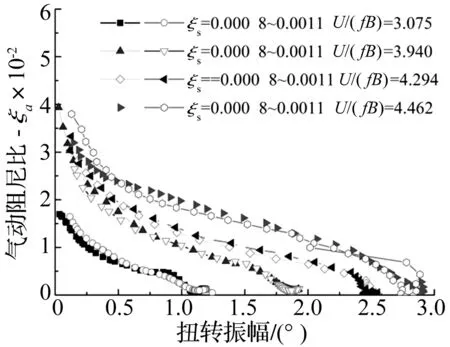
图13 非线性气动阻尼ξa(ρ)随约化风速U*变化关系(3°攻角)Fig.13 Effect of reduced wind speed U* on nonlinear aerodynamic damping ratio ξa(ρ) (attack angle 3°)

在考虑了上述ξs(ρ)和ξa(ρ)曲线的变化趋势之后，将两者的总体趋势绘于图14中，软颤振的机理可以作如图14所示的解释：当风速较低时，气动阻尼曲线完全在结构阻尼曲线之下，系统的总阻尼为正，风场对振动系统的任何扰动都是衰减的，此时未发生软颤振；随着风速的增加，气动阻尼曲线ξa(ρ)不断向上抬升，开始与结构阻尼曲线ξs(ρ)相交，当振幅小于两条曲线交点对应的振幅时，ξa(ρ)位于ξs(ρ)之上，系统总阻尼为负，模型振幅不断增大，当振幅大于两条曲线交点对应的振幅时，ξa(ρ)位于ξs(ρ)之下，系统总阻尼比为正，模型振幅则不断衰减，可知两条曲线交点对应的振幅即为软颤振的稳定振幅；当风速继续增大，气动阻尼曲线ξa(ρ)继续向上抬升，造成ξa(ρ)和ξs(ρ)的交点沿着振幅增大的方向移动，从而使得软颤振稳定振幅进一步提高，由图3所示的软颤振振幅随约化风速的近似直线关系，可知ξa(ρ)和ξs(ρ)的交点随U*的变化率在振幅轴ρ上的投影应该是近似匀速的。对于气动阻尼的非线性效应不太强的-3°攻角姿态，在较高的折算风速时，ξa(ρ)曲线随振幅的降低效应并不太明显，此时ξa(ρ)可能完全位于ξs(ρ)曲线的上方，两者没有交点，因而无法达到一个稳定的振幅，由此出现了发散性颤振，但由于非线性阻尼比ξa(ρ)的影响，振幅在发散过程中仍然不是以指数形式增加，而是要缓慢得多。

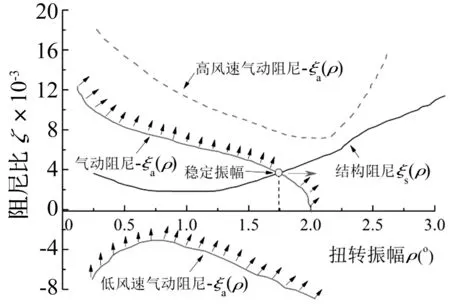
图14 软颤振的机理示意图Fig.14 Schematic diagram of soft flutter mechanism

4 结 论

本文采用弹簧悬挂节段模型测振的方法，对双边肋断面的软颤振现象进行了研究。在经典线性自激力模型的颤振导数中计入瞬时扭转振幅的影响，提出一个适用于大振幅振动的非线性自激力模型，并对软颤振的机理进行了初步探讨，主要结论如下：

(1) 由于自激力的非线性效应，双边肋断面在3°和0°攻角时，均出现了明显的软颤振现象，在-3°攻角时出现了软颤振、多个稳定振幅和缓慢发散性颤振等复杂的非线性振动现象。软颤振发生在扭转模态内，以单自由度的扭转振动为主，弯扭耦合效应比较微弱。

(2) 将Scanlan线性自激力模型的颤振导数拓展为瞬时扭转振幅的函数，从而可以计入振幅对气动参数的影响。通过软颤振响应的数值计算和试验结果的对比，验证了所提出的非线性自激力模型的可靠性。

(3) 软颤振是由非线性自激力引起的，而自激力非线性效应主要体现为气动阻尼的非线性，气动刚度的非线性效应较弱。由气动阻尼参数随振幅的变化趋势，可以对软颤振的机理进行解释。

[1] SIMU E, SCANLAN R H. Windeffects on structures: fundamental and applications to design, 3rd edition [M]. John Wiley & Sons, INC, New York, USA, 1996.

[2] 项海帆,葛耀君,朱乐东,等.现代桥梁抗风理论与实践[M].北京:人民交通出版社,2005.

[3] SCANLAN R H, TOMKO J J. Airfoil and bridge deck flutter derivatives [J]. Journal of Engineering Mechanics, ASCE, 1971, 97(6), 1717-1737.

[4] 徐旭，曹志远.气动耦合扭转非线性振动的稳定性分析[J].非线性动力学报,1999,6(3):228-234. XU Xu, CAO Zhiyuan. Stability analysis of nonlinear aerodynamic-coupled torsional vibration [J]. Journal of Nonlinear Dynamics in Science and Technology, 1999,6(3):228-234.

[5] 徐旭，曹志远.柔长结构气固耦合的线性与非线性气动力理论[J]. 应用数学和力学, 2001, 22(12): 1299-1308. XU Xu, CAO Zhiyuan. Linear and nonlinear aerodynamic theory of interaction between flexible long structure and wind [J]. Applied Mathematics and Mechanics, 2001, 22(12): 1299-1308.

[6] 张朝贵.桥梁主梁“软”颤振及其非线性自激气动力参数识别[D]. 上海:同济大学,2007.

[7] 刘十一, 葛耀君. 基于非线性微分方程的时域自激力模型[C]//第十六届全国结构风工程学术会议暨第二届全国风工程研究生论坛,成都, 2013.8.

[8] LIU Shiyi, GE Yaojun. Fitting method of nonlinear differential equations for aerodynamic forces ofbridge decks. Proceedings of the 12thAmericas Conference on Wind Engineering, Seattle, Washington, USA, 2013.

[9] WU Teng, KAREEM A. A nonlinear convolution scheme to simulate bridge aerodynamics[J]. Computers and Structures, 2013, 128:259-271.

[12] NAPRSTEK J, POSPIIL S. Post-critical behavior of a simple non-linear system in a cross-wind [J]. Engineering Mechanics, 2011, 18:193-201.

[13] DIANA G, RESTA F, ROCCHI D. A new approach to model the aeroelastic response of bridges in time domain by means of a rheological model [C]//Proceedings of 12th International Conference on Wind Engineering, Cairns, Australia, 2007: 1-6.

[14] DIANA G, et al. Aerodynamic hysteresis: wind tunnel tests and numerical implementation of a fully nonlinear model for the bridge aeroelastic forces [C]//Proceedings of the 4th International Conference on Advances in Wind and Structures (AWAS’08), Jeju, Korea, 2008:29-31.

[15] 王骑,廖海黎,李明水,等. 桥梁断面非线性颤振自激力经验模型 [J]. 西南交通大学学报, 2013,48(2): 271-277. WANG Qi, LIAO Haili, LI Mingshui, et al. Emperical mathematical model for nonlinear motion-induced aerodynamic force of bridge girder [J]. Journal of Southwest Jiaotong University, 2013, 48(2): 271-277.

[16] 朱乐东，高广中. 典型桥梁断面软颤振现象及影响因素 [J]. 同济大学学报(自然科学版), 2015, 43(9): 1289-1294. ZHU Ledong, GAO Guangzhong. Influential factors of soft flutter phenomenon for typical bridge deck sections [J]. Journal of Tongji University (Natural Science), 2015, 43(9): 1289-1294.

[17] AMANDOLESE X, MICHELIN S, CHOQUEL M. Low speed flutter and limit cycle oscillations of a two-degree-of-freedom flat plate in a wind tunnel [J]. Journal of Fluids and Structures, 2013, 31:244-255.

[18] DAITO Y, MATSUMOTO M, ARAKI K. Torsional flutter mechanism of two-edge girders for long-span cable-stayed bridge [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90: 2127-2141.

[19] 许福友,陈艾荣.印尼Suramadu大桥颤振试验与颤振分析[J].土木工程学报, 2009, 42(1): 35-40. XU Fuyou, CHEN Airong. Flutter test and analysis for theSuramadu Bridge in Indonesia [J]. China Civil Engineering Journal, 2009, 42(1): 35-40.

[20] RICE H J. Identification of weakly non-linear systems using equivalent linearization [J]. Journal of Sound and Vibration, 1995, 185 (3), 473-481.

[21] NAYFEH A H, MOOK D T. Nonlinear oscillations [M]. John Wiley & Sons, New York, USA, 1979.

[22] GAO G Z, ZHU L D. Nonlinearity of mechanical damping and stiffness of a spring-suspended sectional model system for wind tunnel tests [J], Journal of Sound and Vibration, 2015, 355: 369-391.

A nonlinear self-excited force model for soft flutter phenomenon of a twin-side-girder bridge section

ZHU Ledong1, 2, 3, GAO Guangzhong1, 2

(1.State Key Laboratory of Disaster Reduction in Civil Engineering,Tongji University, Shanghai 200092, China;2.College of Civil Engineering, Tongji University, Shanghai 200092, China;3. Key Laboratory of Wind Resistance Technology of Bridges of Ministry of Transport,Tongji University, Shanghai 200092, China)

To investigate the soft flutter phenomenon, i.e., nonlinear post critical limit cycle oscil1ation (LCO) of a twin-side-girder section, a series of spring-suspended sectional model tests were conducted. Experimental results showed that the sectional model exhibits violent soft flutter phenomena in post flutter range; the observed soft flutter is a quasi-harmonic nonlinear torsional vibration with a slight bending-torsion coupling effect; the classical linear self-excited force model by Scanlan is not applicable to soft flutter. To model the aerodynamic nonlinearity during large-amplitude oscillation of soft flutter, a nonlinear self-excited force model was proposed by expressing flutter derivatives of the classical Scanlan’s linear model as functions of transient torsional vibration amplitude. The identified results of the amplitude-dependant flutter derivatives showed that the nonlinearity is strong for the aerodynamic damping and very weak for the aerodynamic stiffness. The feasibility of the proposed model and the reliability of the identified aerodynamic parameters were verified by comparing the computed vibration responses of soft flutter with the corresponding experimental data. The mechanism of soft flutter was then explored with the identified nonlinear relationships of aerodynamic damping and structural damping with respect to the transient torsional vibration amplitude.

twin-side-girder section; soft flutter; post-critical LCO; nonlinear self-excited force model; nonlinear aerodynamic damping; soft flutter mechanism

国家自然科学基金面上项目(51478360)；国家自然科学基金重大研究计划集成项目(91215302)

2015-05-29 修改稿收到日期：2015-09-21

朱乐东 男，博士，研究员，博士生导师，1965年生

高广中 男，博士生，1988年生

U441.3

A

10.13465/j.cnki.jvs.2016.21.005