间隙对齿轮-转子-轴承系统弯扭耦合振动的影响分析
2016-12-15高雪媛邸薇薇李媛媛
向 玲, 贾 轶, 高雪媛, 邸薇薇, 李媛媛
(华北电力大学 机械工程系,保定 071003)
间隙对齿轮-转子-轴承系统弯扭耦合振动的影响分析
向 玲, 贾 轶, 高雪媛, 邸薇薇, 李媛媛
(华北电力大学 机械工程系,保定 071003)
综合了动态侧隙、齿面摩擦、齿轮偏心及时变啮合刚度等因素,建立了齿轮-转子-滚动轴承系统的弯扭耦合非线性动力学模型,通过分析动态侧隙及轴承间隙对系统的影响来探究轴承端与齿轮端振动之间的耦合作用关系。结果表明:相对于无间隙系统,动态侧隙下轴承端的径向振动在高速区较为强烈,而齿轮的扭转振动在整个转速区幅度较大,随转速变化时系统提前通过非线性跳跃进入主共振区。动态侧隙的改变对轴承端的振动影响不大,但对扭振作用明显;轴承间隙的大小对系统径向和扭转振动有着显著影响,随着轴承间隙的变化,两者的时域特征及频谱存在着规律性的变化;另外,轴承间隙直接影响着动态侧隙的大小。分析结果对含间隙齿轮转子系统的研究具有重要的理论与工程价值。
动态侧隙;弯扭耦合;轴承间隙;偏心;啮合刚度
齿轮系统是机械系统的重要组成部分,长期以来,人们对齿轮传动系统的振动特性进行了各种各样的理论和实验研究,也不断揭示了齿轮系统的运行机理及存在的一些复杂的非线性现象。其中KAHRAMAN[1-2]通过建立多样化的动力学模型对含间隙齿轮系统的非线性动力学特性进行了一系列深入的研究,为后续学者进行相关研究奠定了理论基础。MORADI[3]等利用多尺度法研究分析了设计参数对齿轮非线性系统主共振、超谐和次谐共振的影响。LI等[4]研究了轮齿表面粗糙度,润滑温度及其他工况参数对齿轮系统振动特性的影响,结果表明这些因素对系统的弯扭耦合振动及动态啮合起着重要作用。FARSHIDIANFAR等[5]建立了含齿侧间隙和径向间隙的动力学模型,着重分析研究了齿轮系统的混沌和分岔现象。高洪波等[6]综合考虑了动态侧隙、偏心及摩擦等因素着重研究了齿轮全齿磨损和偏心磨损下系统的振动特性。李朝峰等[7]建立了含齿轮偏心及轴承非线性的齿轮-转子-轴承系统弯扭耦合动力学模型,并分析了各设计参量对系统振动响应的影响,但该模型中并没有考虑啮合刚度的时变性、齿侧间隙以及齿面摩擦的作用。
本文基于上述研究,综合考虑了动态侧隙、齿轮偏心、轴及轴承等非线性因素,建立了齿轮-转子-轴承传动系统的非线性动力学模型,并对其进行了数值仿真分析。着重研究了齿侧间隙、轴承间隙对系统弯扭耦合振动特性的影响及两者的耦合作用关系。
1 动力学模型
图1所示为动态条件下齿轮-转子-轴承传动系统的集中质量模型,各轴承部分几何坐标原点为A、B、C、D。主/从动齿轮的理想中心O和O’均位于轴承孔的理想中心线上,按图示主坐标系(x,y,z)的方向可得到各轴承及齿轮的固定坐标系。Oi,Gi(i= 1,2)分别为主从动齿轮的形心和质心。两轴与各相应轴承的集中质量部分对应的当量质量为mbi(i= 1,2,3,4)。主/从动齿轮的质量为mi(i= 1,2),对应质心的转动惯量分别为Ji(i= 1,2)。系统输入端电动机转子及输出端负载转子对应的转动惯量为Jm、Jp。
假设不考虑齿轮的轴向窜动,在xoy平面上,现设主、从动齿轮的形心坐标为O1(x1,y1),O2(x2,y2),对应的质心坐标为G1(xo1,yo1)),G2(xo2,yo2),偏心距O1G1=ρ1,O2G2=ρ2。主/从动轮的转角为φ1,φ2,对应的振动角位移分别为θ1,θ2。设主从动轮的初始旋转角均为0。以主动轮转动方向为正方向,则由几何关系可得
(1)
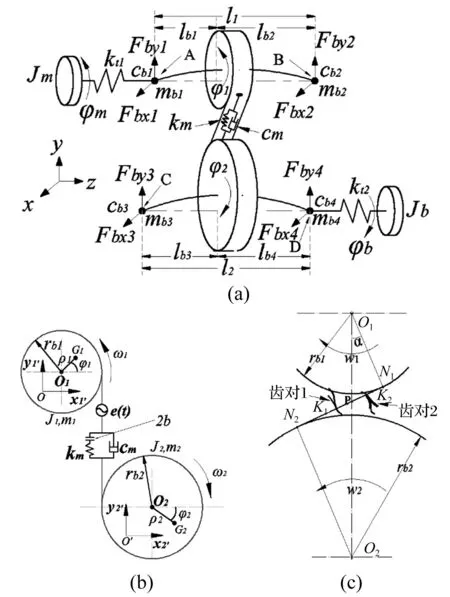
图1 齿轮传动系统的动力学模型Fig.1 Dynamic model of gear transmission system
另设轴承旋转中心的位移坐标 (xbi,ybi) (i= 1,2,3,4),根据轴的变形协调条件可知,主被动轴在两齿轮旋转中心位置x,y方向的弹性变形大小可表示为
(2)
式中:ξ1=lbi/lj(i= 1,2,j= 2;i= 3,4,j= 2),如图1中所示,l1,l2为主从动轴在两轴承间的长度;lbi(i= 1,2,3,4)为主从动轴上齿轮旋转中心到相应轴承质心的距离。由系统的几何关系可得,在某个啮合时刻轮齿的啮合力如式(3);f(…)为间隙性非线性函数。
DTE=rb1φ1-rb2φ2+y2-y1+ρ2sinφ2-ρ1sinφ1
(3)
1.1 摩擦力及摩擦力矩
齿面摩擦力可由齿轮啮合的动态啮合力得到,如式(4),其中,λi,μi分别为摩擦力方向系数和时变摩擦系数,对于λi,啮合点在节点以上取“+1”,反之则取“-1”。
(4)
对于μi,其大小随啮合位置作周期变化,为了接近现实,本文采用经典的Buckingham半经验公式[8]:
(5)
其中Vsi为齿廓接触点的相对滑动速度,由文献[8]可知
Vsi=w1×S1i-w2×S2i
(6)
式中:S1i,S2i为齿对i之间的摩擦力对齿轮1、齿轮2的摩擦力臂,由图1(c)可知,w1,w2分别为两齿轮的角速度;对于S1i/S2i,当i=1时为K1N1/K1N2,当i=2时为K2N1/K2N2;当0<ε<1, 力臂可表示为
(7)
式中:ra1,ra2为主从动轮的齿顶高半径,t1为一个双齿啮合时间,Pb为基圆节距,α为压力角。
1.2 动态侧隙
齿轮安装时要留有一定的齿侧间隙,其随着齿轮中心距或齿厚的变化而变化,当齿轮系统由于轴承振动或偏心引起中心距变化时,齿侧间隙可表示为:
b=2b0+2a0cosα0(tanα′-tanα0+α0-α′)
α′=arccos(a0cosα0/a′)
a′=
(8)
式中:a0,α0为初始中心距和压力角,a’,α’为实际啮合过程中的中心距和压力角,b0为初始单边齿侧间隙,这样动态啮合力式(3)中的非线性函数表示为
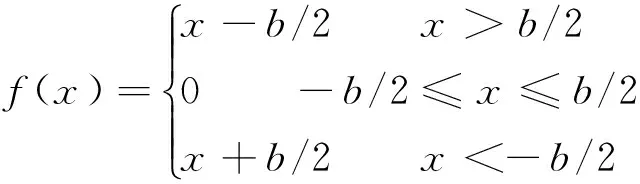
(9)
1.3 时变啮合刚度
在直齿轮传动时,轮齿的变形及刚度均作周期变化且存在突变;有不少研究将啮合刚度近似为矩形波或傅里叶级数的形式,但与实际结果存在一定差异,本文采用文献[9]的能量法并结合文献[10]的修正法进行计算。这里仅给出一对齿综合啮合刚度的计算公式:
k=
(10)
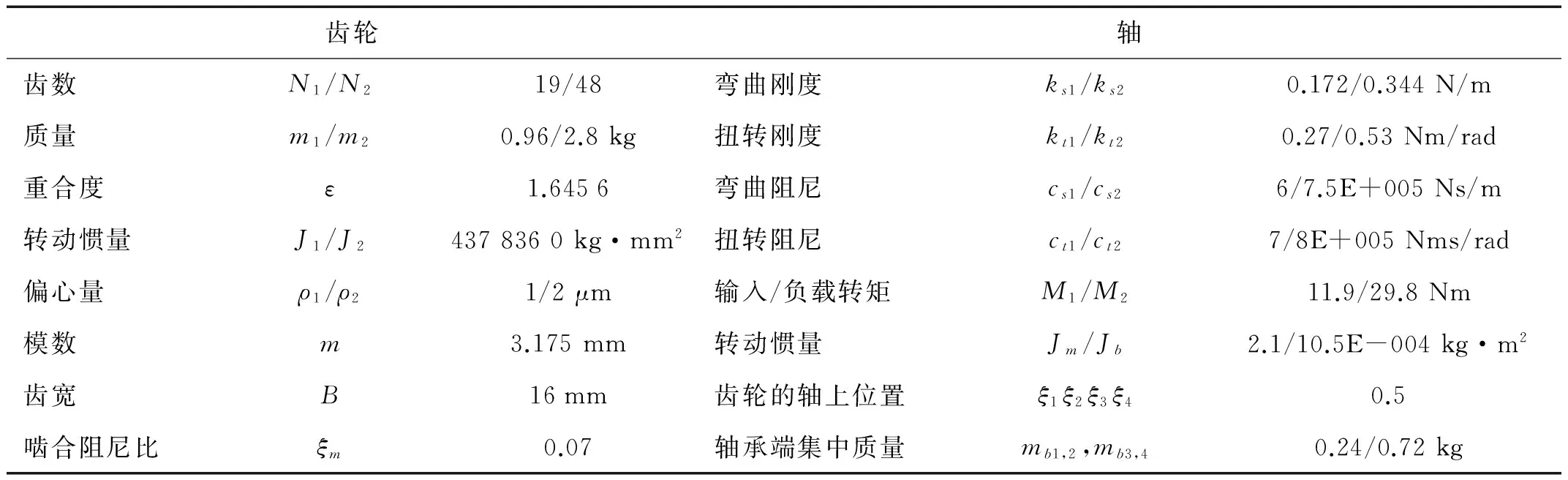
各参数的定义及计算公式详见文献[9-10]。当两对齿同时参与啮合时,另一对齿的啮合刚度计算同上式,将两对齿啮合刚度相加即为齿轮副的综合啮合刚度。为了后续分析,这里给出经计算得到的一个啮合周期内的时变刚度曲线(图2),齿轮参数如表1所示。
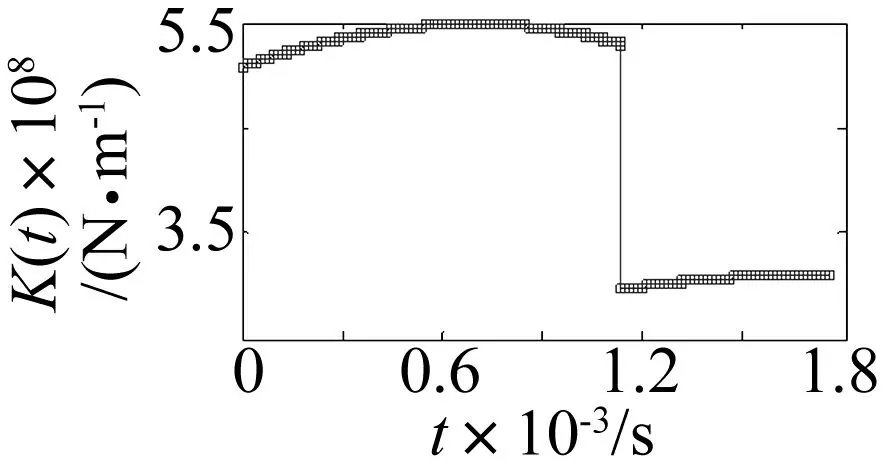
图2 时变啮合刚度Fig.2 Time-varying mesh stiffness
1.4 非线性轴承力模型
图3为滚动轴承模型示意图,假定轴承的内圈与旋转轴、外圈与轴承座均为刚性连接,滚动体等间距排列且与滚道之间为纯滚动。轴承变形主要是滚珠和滚道的接触变形。
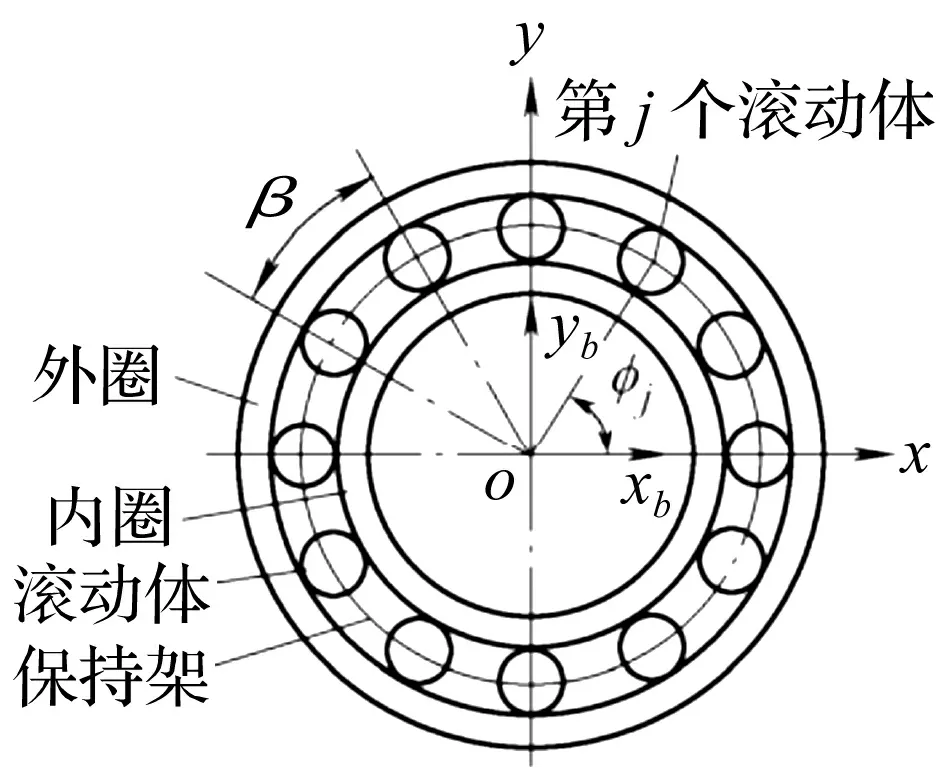
图3 滚动轴承模型Fig.3 Rolling bearing model
图3中第j个滚珠与滚道的法向接触变形可表示为
δj=xbcosφj+ybsinφj-r0
(11)
式中:xb,yb分别为内圈中心在x,y方向的振动位移,r0为滚动轴承间隙,φj为第j个滚珠的位置角。轴承的非线性力可由轴承运动学和赫兹基理论推得[11]。
(12)
式中:nb为滚珠个数;Kc为赫兹接触刚度系数;H(x)为Heaviside函数,当x>0,该函数返回值为1,反之,返回值为0,其反映着接触变形与接触力的关系。
根据以上分析,进一步引入系统的广义坐标列阵[φmx1y1φ1x2y2φ2xb1yb1xb2yb2xb3yb3xb4yb4φb]T,求得系统的动能,势能和耗散函数,根据拉格朗日方程可得系统的非线性动力学方程,如式(13)。
式中xi,yi为主/从动轮沿x,y方向的振动位移;xbi,ybi则对应主/从动轴轴承在x,y方向的振动位移;ksi,kti(i=1,2)分别为输入轴和输出轴的弯曲刚度和和扭转刚度;csi,cti(i=1,2)则对应轴的弯曲阻尼和扭转阻尼;cbxi,cbyi(i=1,2,3,4)为轴承的径向阻尼;Fbxi,Fbyi为轴承的非线性力;M1,M2为输入端和输出端扭矩。
2 间隙对系统弯扭耦合振动的影响
间隙对系统振动特性及啮合状态有着重要影响,有必要对系统的动力学响应及各间隙的作用进行详细分析。因为,式(13)综合考虑了时变刚度和动态侧隙等强非线性因素,方程参数量级差别较大,求解时易出现病态和不收敛问题,因此,采用求解稳定性及精度较高的ode15s对其进行求解,首先将方程写成状态方程的形式(降阶),然后设置求解精度(相对和绝对精度均为1.0×10-9)进行计算。系统参数如表1所示,轴承均选择SKF6200,查阅轴承手册可得轴承的详细参数。
2.1 齿侧间隙的影响分析
齿侧间隙直接影响着轮齿的啮合状态,为了分析齿侧间隙大小对系统动力学响应的影响规律,分别取初始齿侧间隙b0为0 μm,0.05 μm,0.1 μm,并以无间隙作为对比对系统进行数值仿真,此时主从动轴轴承的间隙分别为1 μm,2 μm。
首先在整个转速内分析系统的动力学响应,图4是主从动轴上轴承(编号1和3)沿x,y方向振动位移、动态传动误差(DTE)随主动轴转频(f)变化的RMS(均方根值)曲线。从图中看出,无间隙时,系统在f=100(啮频fm=1 900) 和f=192(fm=3 648)发生扭转方向的共振,轴承端在f=100和f=202(fm=3 838)发生x方向的共振在y方向未发现共振峰的存在,注意到扭振和轴承端径向振动主共振频率略有差别。而对于动态间隙系统,同样在f=100和f=166处出现了共振峰,且弯振和扭振的峰值频率基本接近;当增大b0时,峰值及固频变化微弱。另外,扭振的RMS随b0增大明显增大(图4(a)),同时动态侧隙也随之增大(如图4(f)),但轴承端的径向振动变化较小,说明了初始齿侧间隙对于轴承端振动影响较弱。其次,由图可知,对于扭振,动态侧隙下的RMS比无间隙时大很多,这是因为动态侧隙综合考虑了横向和径向振动,其促使了扭振的加强,由式(8)也可判断;而对于轴承端振动,在低速区,动态侧隙下的均方根值和无间隙时相差不大,而在高速区,前者明显比后者大,如图4(b)~图4(e)所示。总之,相对于无间隙模型,动态侧隙在整个转速区内对系统的扭振影响显著,而在高速区则对轴承端径向振动影响较大。另外,系统在进入主共振区(第二个峰值区域)时产生了跳跃,这种跳跃并没有随b0的增大而变化,但对于无间隙系统,系统在进入此区域时是连续的,这侧面反映了间隙的非线性作用。
对于轮齿的啮合状态,对比图5曲线可知,在主共振区域,无间隙系统啮合力的各项指标明显偏大,但共振区出现滞后;而在其他转速区域,啮合力各指标相差较小。并且,由图5(c)可知,在共振区,有/无间隙系统均处于双边冲击状态,而动态间隙的啮合力相对较小,其存在减弱了共振区的轮齿冲击;在其他区域,轮齿处于无冲击状态,动态侧隙的改变并未影响该状态。
(13)
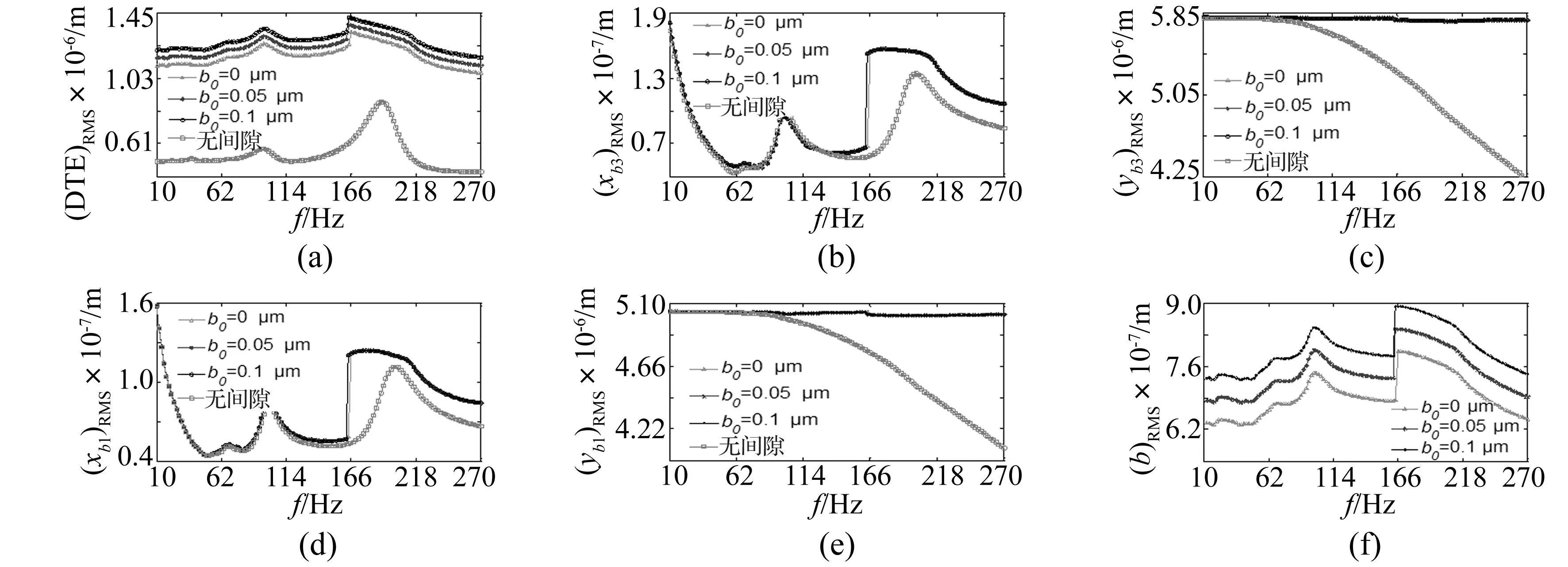
图4 各参量的RMS曲线Fig.4 RMS curve of all vibration variables

图5 啮合力的均方根值、最大值及最小值曲线Fig.5 RMS、Maximum and Minimum curve of dynamic mesh force
进一步分析动态侧隙对系统振动特性的影响,设置f=30 Hz,b0=0.1 μm,这里从频谱的角度进行分析。首先确定该工况下各振动量的频率成分,图6为轴承端径向振动的时间历程图及频谱图,以下主/被动轴轴承端分别用B1和B2表示。对于横向(x)振动:B1处以2f1(f1=30 Hz,轴频)频率为主,并出现了高倍轴频、啮频(fm=N1*f1=570 Hz)及其二倍频成分,如图6(a2);与之类似,B2处以2f2(f1*N1/N2=11.875 Hz)频率为主,并出现了fm及其二倍频成分,如图6(c2)。对于纵向(y)振动:B1处以2f1频为主,且存在fm及其倍频成分,如图(b2);B2处以2f2频为主,且存在fm及其倍频成分,如图6(d2)。另外注意到,B1/B2径向(x,y)振动在低频处的频带较宽且连续,同时存在其他频率成分,这应该与轴承的非线性有关。对于扭转振动:时域图(图7)中可明显看到冲击的存在,且DTE及动态啮合力(DMF) 的频带较宽。
DTE频谱以fm及其倍频为主,且存在2f1、2f2及其他随机频率成分(表现为低频)。DMF频谱以fm及其倍频为主,且出现了f1、f2及以其倍频为频率间隔的频率成分,另外也存在一些随机频率成分,总之DMF频带的频率成分较复杂。
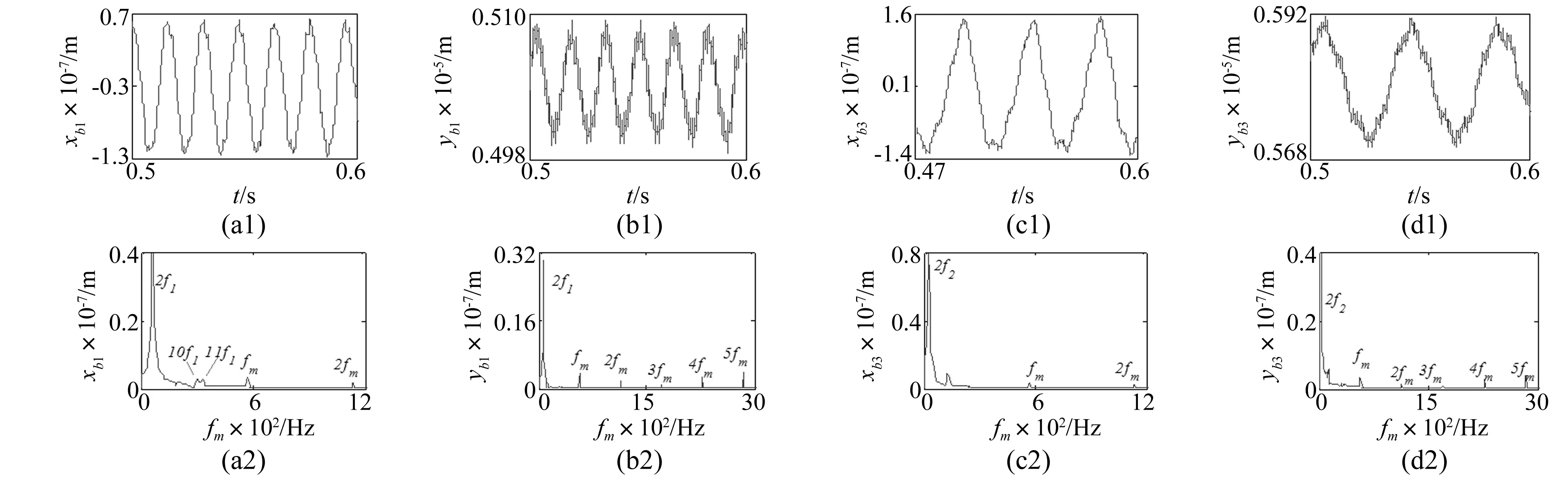
图6 轴承端径向振动的时域波形及频谱Fig.6 Transverse vibration waveform and spectrum diagram of bearing end

图7 DTE和动态啮合力的时域波形及频谱Fig.7 Waveform and spectrum diagram of DTE and DMF
为了全面了解动态侧隙的作用,图8给出了各振动量随初始齿侧间隙b0变化的三维频谱图。对比各图可知,当b0变化时,无论轴承端的径向振动或是齿轮的扭振,各频谱中主要频谱成分没有明显的增减。结合图4可知,b0的变化对于轴承端的振动影响并不大。另外,b0对于扭振 (DTE)幅度有显著的影响,但对DMF影响较小,同时结合式(3)及式(9)可知,初始侧隙对动态侧隙系统扭振的影响类似于一个线性增加的常量,其并未对DMF产生较大影响,同时该常量在频谱中相当于直流分量,因此各频率成分并未随b0的变化明显改变。当然,上述结果仅限于初始侧隙在允许范围内变化时得到。

图8 各振动参量的三维频谱图Fig.8 Three-dimensional spectrum of all vibration variables
2.2 轴承间隙的影响分析
首先主/从动轴轴承用C1/C2表示,主/从动齿轮用G1/G2表示。为了分析轴承间隙的影响规律,分别取C1间隙r1为0.5 μm,1 μm,2 μm及4 μm,为了保持C1/C2间隙的定量关系,C2间隙设为2r1,b0设为0.1 μm。图9为G1/G2径向振动位移、DTE及动态侧隙随主动轴轴频f变化的RMS曲线。
由图可见,对于G1/G2的横向(x)振动(如图9(b)、(d) 所示):系统在f=100 Hz(fm=1 900 Hz) 和f=166 Hz(fm=3 154 Hz)处出现共振峰,随着C1/C2间隙的增加,在中高转速区,曲线均小幅上移,对应振动的加强;而在低速区(多为工作转速区),G1/G2的各振动曲线相差较小;仅在r1=4 μm时,主动轮振动明显较弱,而被动轮振动较强,这是由于间隙相对过大而引起轴承非线性力剧烈变化而造成的。对于G1/G2的纵向(y)振动(图9(c)、(e)):振动在该方向上随转速变化比较平稳且未出现共振峰;随着C1/C2间隙的增加,曲线整体上移,振动明显加强,说明了间隙的增加使得该向的轴承力或轴的弯曲力明显增加。对于扭振 (图9(a),(f)):当轴承间隙增加时,DTE及动态侧隙的RMS曲线均整体下移,扭振幅度逐步减弱。
关于轴承间隙对啮合状态的影响,图10给出了DMF均方根值,最大值及最小值随轴频f的变化曲线。图中可看到共振峰及跳跃现象的存在;随着C1/C2间隙的增加,各曲线并未明显变化,啮合冲击状态变化很小,说明轴承间隙虽引起径向振动的改变,但这种改变所引起力或力矩的变化并不足以使轮齿啮合状态发生大的改变。
同样,从频谱的角度进一步分析轴承间隙的影响,这里设f=30 Hz,b0=0.1 μm;图11为各振动量随C1间隙r1(r2=2r1)变化的三维频谱图。由于G1/G2径向振动频谱成分基本与轴承端(图6,7)相同,在此不再赘述。
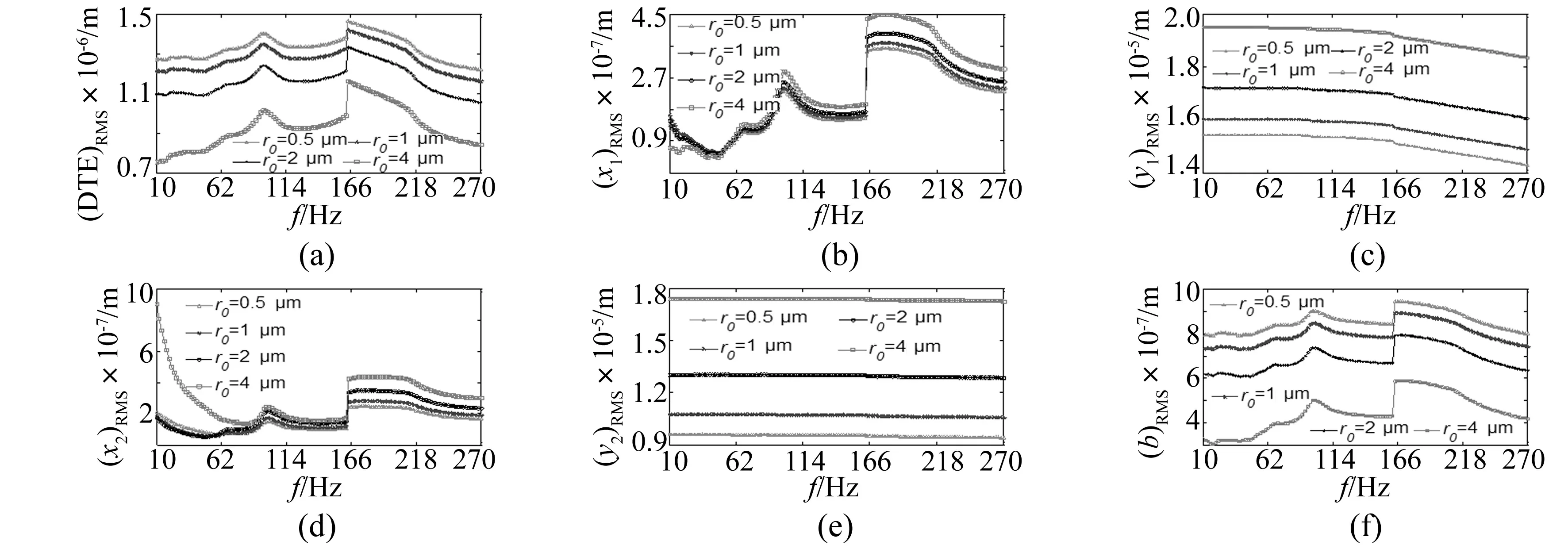
图9 各振动参量的RMS曲线Fig.9 RMS curve of all vibration variables

图10 啮合力曲线Fig.10 RMS、Maximum and Minimum curve of dynamic mesh force
对于G1/G2的横向振动(图11(c), (e)),各倍频成分变化不大,以主频和啮频变化为主。主动轮:主频2f1幅值随r1呈现先增后减再增的趋势,在r1=3.5 μm取最小,如图12(a);啮频fm幅值变化如图12(c),呈现先减后增的趋势,在r1=1.5 μm取最小,但幅值变化不大;被动轮:主频2f2幅值变化同主动轮主频2f1,在r1=1.5 μm取最小(图12(b)),fm幅值在r1=0.4 μm取最小(图12(d))。对比可知G2主频平均幅值比G1大,而G1啮频平均幅值较G2大,G2振动相对较强。
对于G1/G2的纵向振动(图11(d), (f)),仍以主频和啮频为主。主动轮:主频2f1幅值随r1呈现先增后减的趋势,在r1=2.8 μm取最大,如图13(a)所示;啮频fm幅值变化规律性不强,但波动较小(图13(c))。被动轮:主频2f2幅值先增后减再增,在r1=2.8 μm最小(图13(b));而啮频fm幅值则随r1不断跳变,但变化幅度较小(图13(d))。
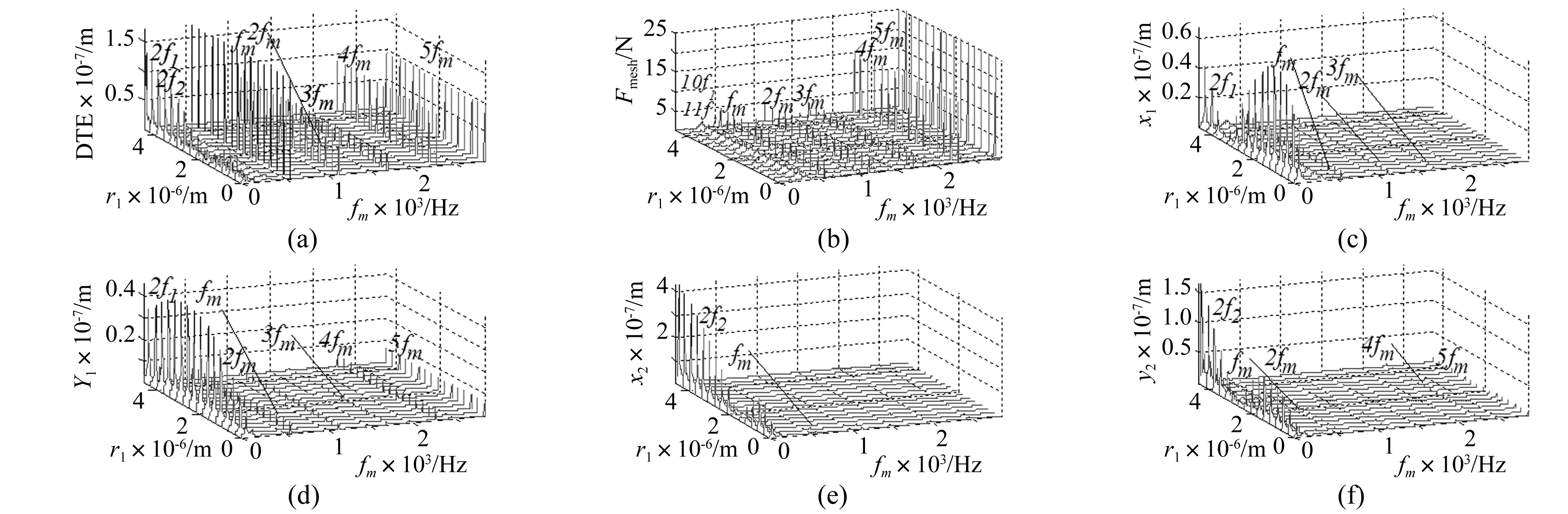
图11 各振动量的三维FFT谱图Fig.11 Three-dimensional spectrum of all vibration variables
对于G1/G2的扭振(图11(a), (b)),振动频带较宽,以啮频及其倍频为主。当r1变化时,扭振频带以G1/G2径向振动的主频(2f1,2f2)变化为主。主动轮:2f1幅值呈现先增后减再增的趋势,同图12(a)中x1向振动,在r1=3.2 μm取最大,如图14(a);2f2幅值也呈现先增后减再增的趋势,同图12(b) 中x2振动,在r1=1.5 μm取最小 (图14(b));啮频fm幅值总体上呈递增趋势,幅值较大(图14(c))。对于啮合力,啮频fm幅值则随r1不断跳变,无明显规律,变化幅度较小(图14(d))。

图12 主/被动轮沿x方向振动的主频幅值随轴承间隙的变化Fig.12 The main frequency amplitude curve via bearing clearance along the X direction

图13 主/被动轮沿y方向振动的主频幅值随轴承间隙的变化Fig.13 The main frequency amplitude curve via bearing clearance along the Y direction

图14 扭振的主频幅值随轴承间隙的变化Fig.14 The main frequency amplitude curve of torsional vibration via bearing clearance
综上所述,合理范围内增大轴承间隙,齿轮纵向(y向)振动明显增强;横向(x向)振动在中高速区内增强,而在低速区内变化较小,而当间隙相对较大时,才会有较大变化;对于扭振,其幅度随轴承间隙的增大则逐渐减小,动态侧隙随之也逐渐减小,但轮齿的啮合状态并未明显变化;另外,轴承间隙的改变并未对系统扭振或弯振的固有频率有所影响;而在频域内,齿轮径向振动的主频(2f1,2f2)幅值受轴承间隙影响较大,其随间隙变化时出现了最值,啮频(fm)幅值同样受间隙的影响,但其变化幅度较小。扭振频谱中包含齿轮径向振动的主频成分(2f1,2f2),轴承间隙对其影响主要表现在对这两种频率成分的影响,而对于谱中啮频及其倍频成分的影响较弱。
3 结 论
本文建立了直齿轮传动系统的弯扭耦合非线性动力学模型,主要研究了初始侧隙对齿轮扭振和轴承端振动的影响、轴承间隙对齿轮扭振和径向振动影响,以此来探究轴承端振动与齿轮端振动之间的作用关系。所得结论如下:
(1) 相对于无间隙系统,动态侧隙下齿轮扭振幅度明显较强;对于轴承端的径向振动,在高速区,动态侧隙系统的振动幅度较无间隙系统大,而在低速区(大部分系统的工作区域),两者相差较小;动态侧隙的影响作用与齿轮转速有着密切的关系。另外,动态侧隙下系统的主共振较无间隙时有所提前,且在进入主共振区域时出现常见的非线性跳跃现象。再者,随着初始侧隙的增加,系统的扭振幅度随之增大,但轴承端的径向振动变化较小;而初始侧隙的增加对系统振动的各主要频率成分影响并不大。
(2) 轴承间隙对齿轮的径向振动和扭转振动影响较大,随着轴承间隙的增加,齿轮的径向振动整体上均有所加强,但扭振的幅度有所降低;轴承间隙对齿轮的啮合力、啮合状态及系统的弯、扭固有频率影响很弱。而在频域内,随着轴承间隙的增加,齿轮径向振动的主频成分均呈现规律性的变化,且在此过程中有最值的出现;扭振频谱的变化表现在以径向振动主频为频率成分的规律性变化,同样有最值的存在。而在各频谱中,啮频及其倍频成分变化较小。这对轴承间隙的选择具有一定的理论指导意义。
(3) 总体上,初始侧隙的变化(动态侧隙随之变化)对轴承端的径向振动影响不大,而轴承端的间隙变化则对齿轮端的径向和扭转振动的影响显著,且轴承间隙直接影响着动态侧隙的大小。
[1] KAHRAMAN A, SINGH R. Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system[J]. Journal of Sound & Vibration, 1991, 146(1):135-156.
[2] KAHRAMAN A, SINGH R. Non-linear dynamics of a geared rotor-bearing system with multiple clearances[J]. Journal of Sound & Vibration, 1991, 144(3):469-506.
[3] MORADI H, SALARIEH H. Analysis of nonlinear oscillations in spur gear pairs with approximated modelling of backlash nonlinearity[J]. Mechanism and Machine Theory, 2012, 51: 14-31.
[4] LI S, KAHRAMAN A. A tribo-dynamic modelof a spur gear pair[J]. Journal of Sound and Vibration, 2013, 332(20): 4963-4978.
[5] FARSHIDIANFAR A, SAGHAFI A. Bifurcation and chaos prediction in nonlinear gear systems[J]. Shock and Vibration, 2014(2):1-8.
[6] 高洪波, 李允公, 刘杰. 基于动态侧隙的齿轮系统齿面磨损故障动力学分析[J]. 振动与冲击, 2014, 33(18): 221-226. GAO Hongbo, LI Yungong, LIU Jie. Dynamic analysis of a spur gear system with tooth-wear faults based on dynamic backlash[J]. Journal of Vibration and Shock,2014,33(18): 221-226.
[7] 李朝峰, 周世华, 刘文明, 等. 齿轮-转子-滚动轴承传动系统的弯扭耦合振动[J]. 航空动力学报, 2014, 29(7): 1543-1555. LI Chaofeng, ZHOU Shihua, LIU Wenming, et al. Vibrationof bending-torsion coupling gear-rotor-rolling bearing transmission system[J]. Journal of Aerospace Power, 2014, 29(7): 1543-1555.
[8] BUCKINGHAM E. Analytical mechanics of gears[M]. Courier Corporation, 1988.
[9] TIAN X. Dynamic simulation for system response of gearbox including localized gear faults[M]. Library and Archives Canada= Bibliothèque et Archives Canada, 2005.
[10] CHAARI F, FAKHFAKH T, HADDAR M. Analytical modelling of spur gear tooth crack and influence on gearmesh stiffness[J]. European Journal of Mechanics-A/Solids, 2009, 28(3): 461-468.
[11] SAWALHI N, RANDALL R B. Simulating gear and bearing interactions in the presence of faults: Part I. The combined gear bearing dynamic model and the simulation of localised bearing faults[J]. Mechanical Systems and Signal Processing, 2008, 22(8): 1924-1951.
Effects of backlash on bending-torsion coupled vibration of a gear-rotor bearing system
XIANG Ling, JIA Yi, GAO Xueyuan, DI Weiwei, LI Yuanyuan
(Mechanical Engineering Department, North China Electric Power University, Baoding 071003, China)
A dynamic model for bending-torsion coupled vibration of a gear-rotor-bearing system was developed considering dynamic backlash, tooth face friction, gear eccentricity and time-varying mesh stiffness. The coupled vibration relationship between bearing end and gear end was investigated by analyzing effects of dynamic backlash and bearing clearance on the system. The results showed that compared with a system without backlash, the radial vibration of the bearing end of the system with dynamic backlash is stronger within a high rotating speed zone, while the amplitude of the gear torsional vibration is larger within the whole rotating speed range; the system with dynamic backlash enters the main resonance region in advance through nonlinear jump; the change of dynamic backlash has little effect on the vibration of bearing end, but it has an obvious effect on the gear torsional vibration; the magnitude of bearing clearance has a significant influence on the radial and torsional vibrations of the system; with the variation of bearing clearance, the time-domain characteristics and frequency spectra of two vibrations vary regularly; moreover, the bearing clearance directly affects the magnitude of dynamic backlash. The results had important theoretical and engineering values for studying gear-rotor systems with clearances.
dynamic backlash; bending-torsion coupling; bearing clearance; eccentricity; mesh stiffness
国家自然科学基金资助项目(51475164)
2015-09-07 修改稿收到日期:2015-11-07
向玲 女,博士,教授,1971年生
TH113
A
10.13465/j.cnki.jvs.2016.21.001
