弹性边界下圆弧拱的自由振动分析

赵章泳， 邱艳宇,2， 王明洋,2， 宋春明,2， 曹 侃

(1.解放军理工大学 爆炸冲击防灾减灾国家重点实验室，南京 210007; 2.南京理工大学 机械工程学院，南京 210094)



弹性边界下圆弧拱的自由振动分析

赵章泳1， 邱艳宇1,2， 王明洋1,2， 宋春明1,2， 曹 侃1

(1.解放军理工大学 爆炸冲击防灾减灾国家重点实验室，南京 210007; 2.南京理工大学 机械工程学院，南京 210094)

工程中圆弧拱的边界不能总被简化为理想的简支或固支形式。为了研究弹性支承对圆弧拱自由振动特性的影响规律，将力、位移等变量无量纲化。根据平衡方程和坐标转换推导得出极坐标下圆弧拱在水平、竖直和转动方向支撑条件为弹性时的边界条件方程。并采用考虑弯曲和轴向变形而忽略剪切变形及转动惯量的自由振动的运动控制方程。运动方程在边界条件情况下，其解仅为关于矢跨比f,细长比s和无量纲刚度阵[K]的函数。采用Runge-Kutta法和行列式搜索法求解运动方程的特征值即无量纲频率Ωi以及特征向量即振型。通过计算发现，与理想支撑相比，弹性支承情况下细长比s对拱自振频率的影响要明显下降。理想支撑情况下圆弧拱的自振频率越高，则弹性支承对其自振频率的影响越小。与水平和竖向弹性支承相比，转动方向弹性支承仅对圆弧拱基频有较大影响。

圆弧拱；自由振动；弹性边界；振型；自振频率；无量纲化

同梁、板、柱等一样，拱结构是工程中最重要的基本构件之一，在不同领域都有着广泛的应用，CHIDAMPARAM 等[1]整理了一百多年来关于拱的研究。由于工程中拱结构的横截面通常都是左右对称的，因此可以将拱的平面内挠曲振动和平面外扭转振动解耦从而分别处理[2]。HENRYCH[3]通过严密的数学推导得出了极坐标下拱结构的考虑弯曲、轴向、剪切变形及转动惯量等因素时的数学模型，并且得到了忽略轴向变形和切向惯性力的情况下拱振型的闭合解。然而对于较浅的拱，其轴向变形对拱自由振动频率具有显著影响[4]。KARNOVSKY[5]着重对在一定程度上满足工程要求的基础上对拱结构进行多自由度离散。在这些研究中，绝大多数采用的都是理想的简支和固支的边界条件。但是在工程中结构的边界不能总简化为理想边界，因此需要研究弹性支撑边界对拱结构自振特性的影响。LEE等[6]曾经对拱结构在径向和转动方向弹性的边界情况进行了研究。然而实际工程中的弹性却总是存在于水平、竖直方向和转动方向的。康婷等[7]曾利用结构动力学中柔度系数的概念对水平弹性支撑下园拱的动力特性进行了计算。本文将更全面的针对圆弧拱在这三种弹性边界下的自由振动特性进行分析。

1 计算模型

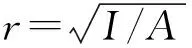
α=4arctan(2f)

(1)

式中：f和s分别为拱的矢跨比和拱的细长比。拱的边界在三个方向上分别具有大小为Kx、Ky、KΘ的弹性支撑。极坐标系下拱轴线上θ位置点的径向和切向位移分别为u、v,转角为ζ。直角坐标系下拱轴线上θ位置点的横向和竖向位移分别为X、Y，转角为Θ；对应的力为Fx、Fy、M。

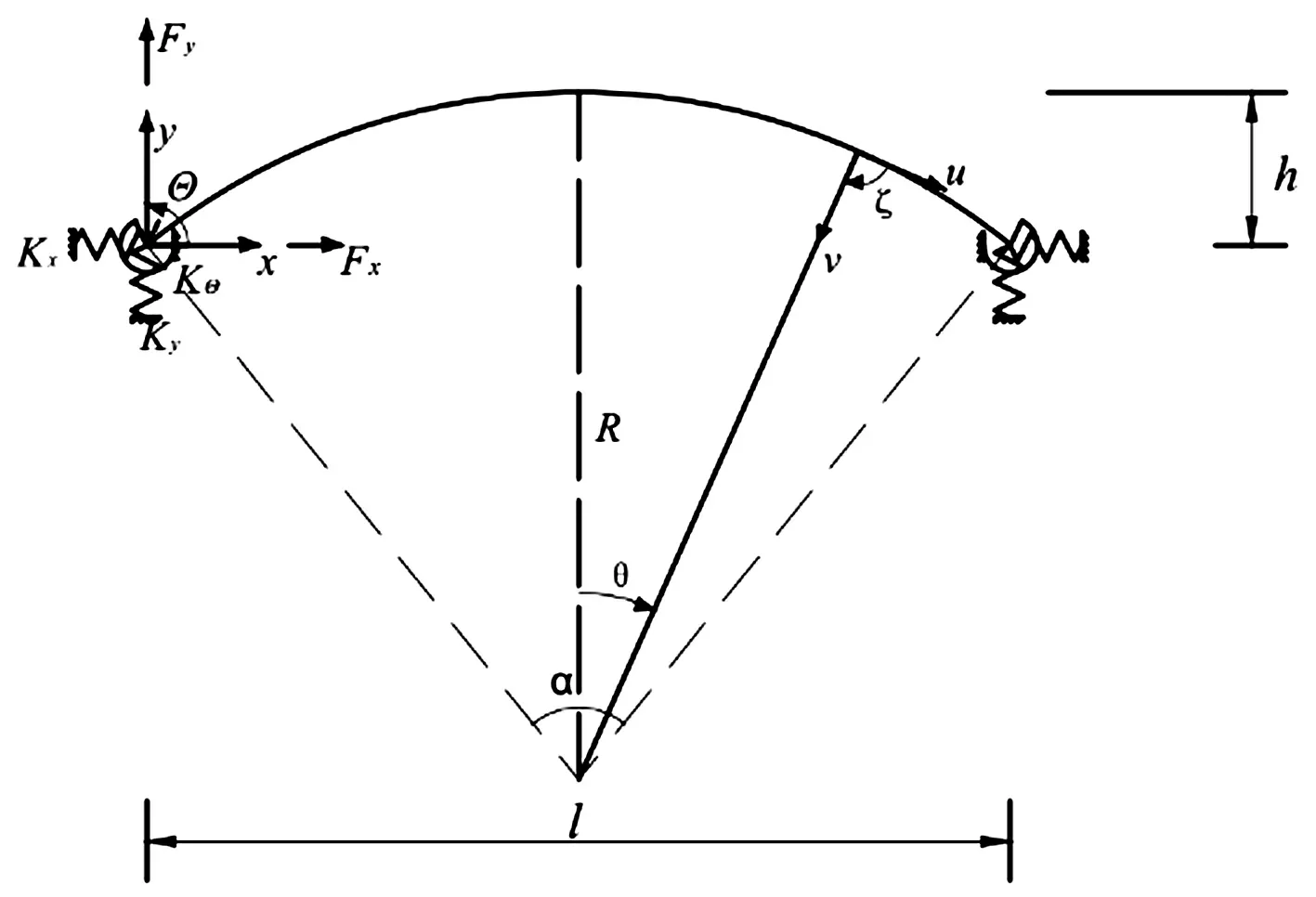
图1 圆弧拱几何模型Fig.1 Circular arch model

图2所示为极坐标系下拱微元体受外荷载作用的内力图，其中N、Q、M分别为轴力、剪力、弯矩，Pr、Pθ分别为微元体所受的径向分布荷载和切向分布荷载。所有位移和力的正方向均同图1、图2中所示一致。

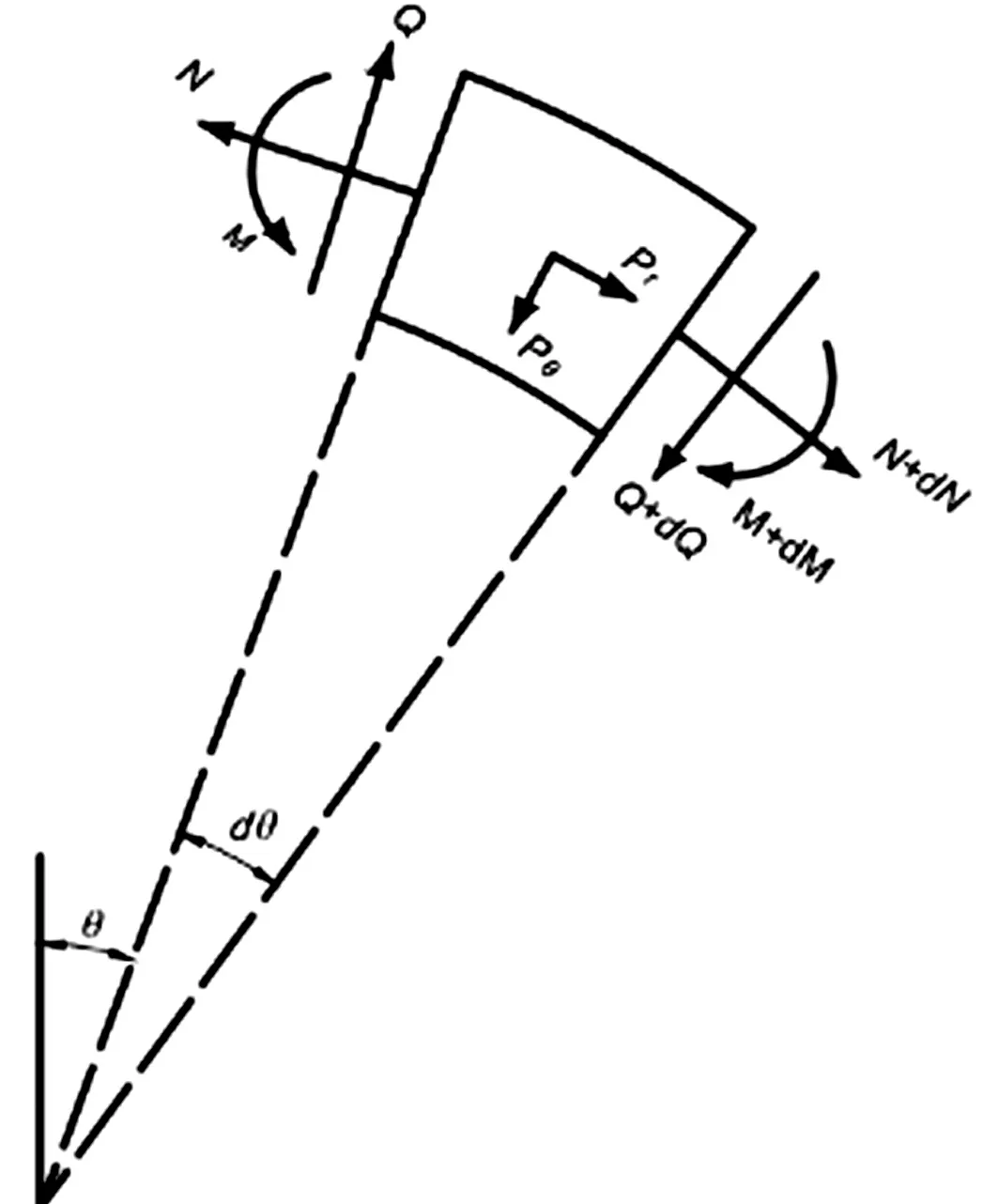
图2 拱微元体受力模型Fig.2 Loads on an arch element

WUNG[8]曾对轴向变形、剪切变形及转动惯量在理想支座下对拱的自振频率的影响进行了详细的研究和计算，表明在细长比s小于0.1的拱中，轴向变形对拱的频率影响远大于其他两项。因此本文亦采用忽略剪切变形和转动惯量的影响，考虑轴向变形的几何方程。HENRYCH[3]推导得到了这种情况下拱的几何、物理和平衡方程分别如式(2)～(4)所示：

(2)

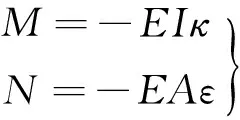
(3)

(4)

需要注意的是，由于忽略了剪切变形，剪力Q是由平衡方程导出而并非物理方程。

为了避免数值计算中可能出现的病态现象以及计算结果的推广，将所有物理量无量纲化。定义无量纲位移为位移与l之比，无量纲弯矩为弯矩与EI/l之比，无量纲力为力与EI/l2之比，转动弹簧无量纲刚度为刚度与π4EI/l之比，线性弹簧无量纲刚度为刚度与π4EI/l3之比[6]。为了方便推导和计算，采用向量形式表示变量：

(5)

向量中元素均已无量纲化，在后文中如无特殊说明，所有变量均为无量纲变量。

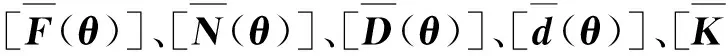
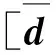
(6)

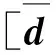
圆拱内力与位移的关系为：

(7)

式中：

如果考虑圆拱的轴向变形而忽略剪切变形和转动惯量，则圆拱自由振动的控制微分方程为[3]：

(8)

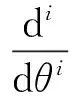
(9)

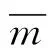
在边界处,θ=±α/2，根据平衡条件有：

(10)

对于弹簧，根据胡克定律：

(11)

又直角坐标和极坐标的转换关系为：

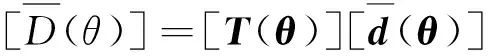
(12)

由于[T]阵为对称正交阵，联立式(10)～(12)可得，在边界处有：

(13)

式中：

联立式(7)、(13)可得：

(14)

式(14)即为弹性边界下圆拱自由振动的边界条件。

2 振型正交性

在振型正交性的推导中，由于对如同时间，质量等变量进行无量纲化并不影响结果，因而在振型正交性推导中并不采用无量纲参数。

记：

[dm(θ,t)]=am[dm(θ)]sin(ωmt+φm)

[dn(θ,t)]=an[dn(θ)]sin(ωnt+φn)

(15)

分别为圆拱按第m、n阶振型振动时的位移函数向量。此时第m阶振型的惯性力向量为

[Im(θ,t)]=

(16)

其中质量阵

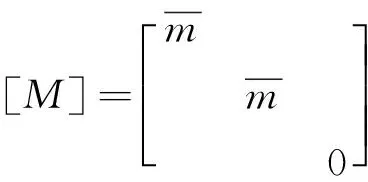
(17)

则在任意时刻t，第m阶振型对应的惯性力按照第n阶振型的虚位移上所做的虚功为

sin(ωmt+φm)sin(ωnt+φn)

(18)

同理在任意时刻t，第n阶振型对应的惯性力按照第m阶振型的虚位移上所做的虚功为:

sin(ωmt+φm)sin(ωnt+φn)

(19)

根据Maxwell-Betti定律，第一组荷载在第二组荷载所引起的变位上所做的功等于第二组荷载在第一组荷载所引起的变位上所做的功，则

Wm,n(t)=Wn,m(t)

(20)

由于

[dm(θ)]T[M]T[dn(θ)]=

[dn(θ)]T[M]T[dm(θ)]

(21)

联立式(18)、(19)、(20)可得

其中

H(t)=amansin(ωmt+φm)sin(ωnt+φn)

(22)

由于对任意时刻t，式(22)成立，且对一般结构，圆频率为重根的情况非常少见[9]。故：

(m≠n)

(23)

此式即为圆拱结构对质量的正交性。

3 数值方法的收敛性及与有限元对比

为了解决微分方程(8)在边界条件(14)下的解，可以使用AL-KHAFAJI[10]以及LEE等[11]介绍的数值方法。通过行列式寻根法和试位法来计算拱的无量纲自振频率Ωi，再根据Runge-Kutta计算拱的振型，其中i表示模态阶数。

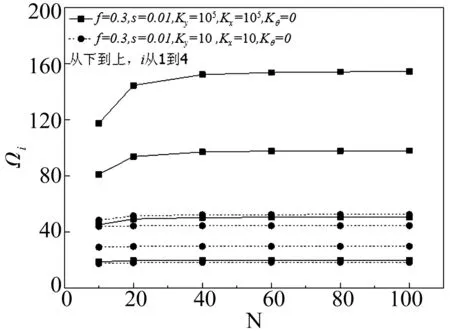
图3 数值方法收敛性分析Fig.3 Convergence analysis of the numerical method

图3为f=0.3,s=0.01前四阶频率随半拱划分段数N的收敛情况。从图中可发现：边界弹簧刚度越小，收敛越快；振型阶数越低，收敛越快；当N>40时，前四阶的自振频率Ωi均能收敛。通过对不同的f、s及[K]的计算，N=40的划分均能收敛。所以在计算中，统一采用了N=40的划分方法。

在对拱的有限元计算中，常用线单元对拱进行离散。采用多少线单元可以得到理想的近似效果是值得注意的。通过对离散后圆拱的刚度阵和质量阵进行无量纲化，同样可以得到其无量纲频率Ωi[4]。将全拱划分为100段，计算得到了几种典型情况下圆拱的无量纲频率Ωi。现将两种方法计算结果列在表1中对比。通过对比发现，当划分段数达到全拱100段后，对于不同矢跨比和细长比，前四阶振型均能满足2%以内的误差。

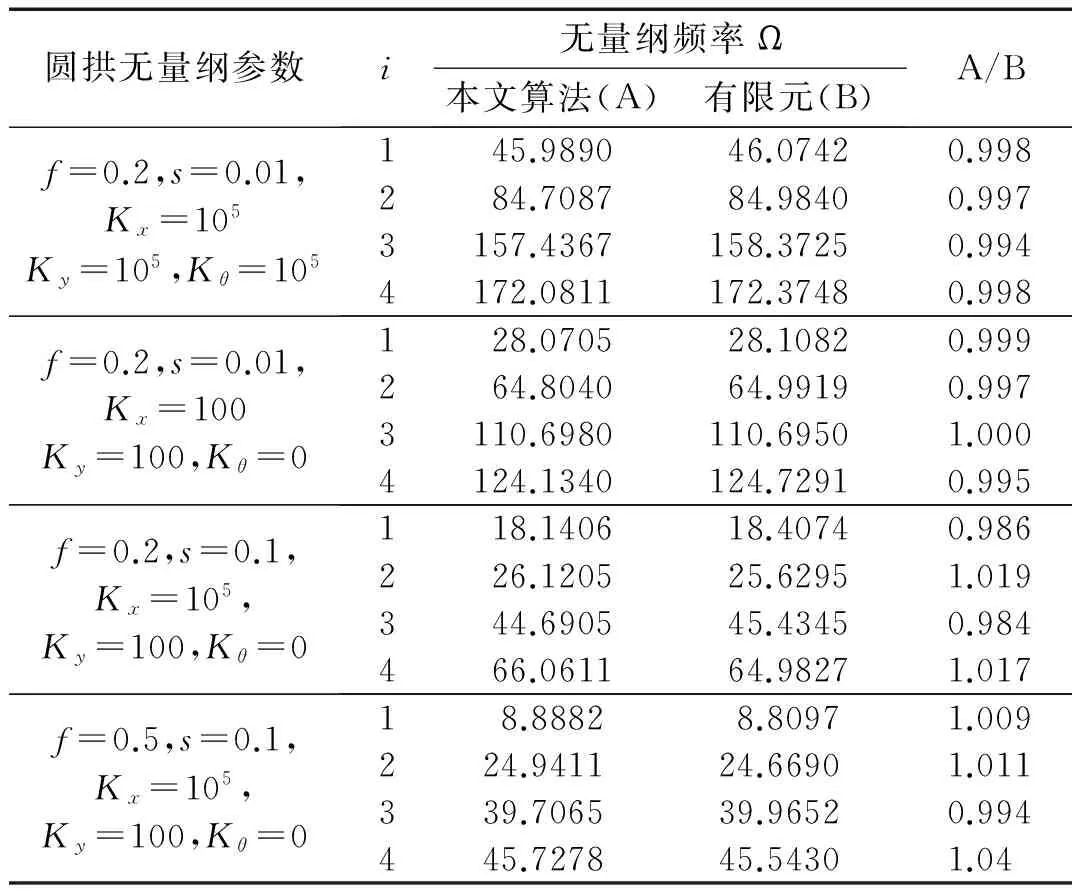
表1 本文Ωi的计算结果与有限元方法对比

4 讨 论

4.1 弹性支撑下矢跨比对频率的影响

对于板拱，当f在0.08附近时，存在着振型的转换点，即当f减小时，拱的一阶振型会从反对称变换成为对称。这种变化意味着曲杆作为拱结构的刚度的丧失，并转化为曲梁[2]。通过本文计算，发现当拱具有弹性支撑时，这种现象将不仅仅出现在浅拱中。如图4所示为s=0.01,kx=∞、ky=100、kΘ=0时圆拱前四阶自振频率Ωi随矢跨比f的变化曲线，图中ia、is分别为反对振动和对称振动的阶数。可以发现第一阶对称振动和第一阶反对称结构自振频率曲线在f=0.4时相交，之后第一振型由对称变为反对称，而在理想边界条件下，这一现象发生在f=0.08附近。且第二阶对称振动和第二阶反对称振动的频率曲线在f=0.07处发生了相交。而在LEE[6]的算例中，高阶的频率曲线只是靠近而并没有相交。说明对于高阶振型，弹性边界也会使得对称与反振型发生互换。

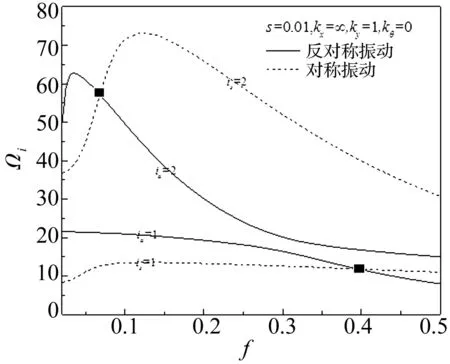
图4 Ωi 随矢跨比f变化曲线Fig.4 The ΩiVersus rise to length ratio f curves

由于这种振型的互换现象，为了研究弹性边界对拱自振频率的影响规律，在计算研究中把反对称振动和对称振动区分开来是很有必要的。

4.2 弹性支撑下细长比对拱频率的影响

圆拱的细长比s对于拱的频率变化的影响是十分显著的[12]。总体来说，矢跨比越小，模态阶数越高，影响越为明显[13]。这是由于s越大，拱轴线的轴向应变与拱截面上远离拱轴线的纤维因弯曲而发生的应变相比，越来越不能忽略[14]。拱的轴向应变在拱振动过程中的影响主要表现在使圆拱的无量纲自振频率下降[8]。如图5所示，在竖向弹性支撑条件下，由于圆拱边界刚度的下降导致拱振动过程中轴力减小，拱轴向变形也相应减小，因而较两端理想支撑情况下，s对Ωi的影响也大大减小。与竖向弹性支承相比，当水平弹性支承刚度减小时，拱中轴力将减小而弯矩将增大[15]，因而s对Ωi的影响将比竖向弹性支撑更弱，在计算中也证明了这一点。

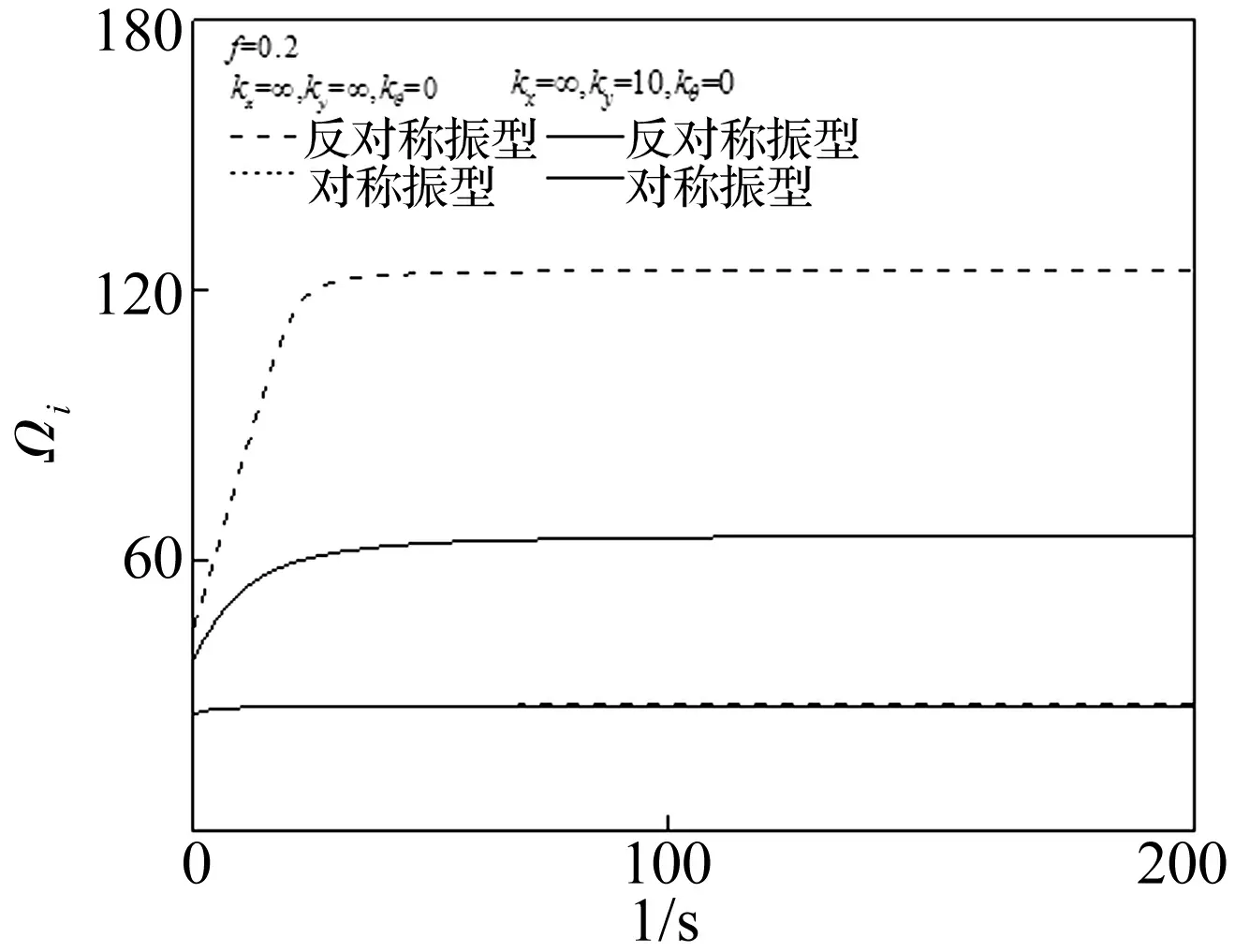
图5 Ωi 随细长比s变化曲线Fig.5 The ΩiVersus slenderness s curves

4.3 弹性支承对拱结构振型与频率影响的关系

为了更深入的研究弹性边界如何使得对称和反对称振动的频率发生改变，将f=0.2,s=0.001的弹性支撑圆拱与理想边界圆拱的前四阶振型绘制于图6中。从中可以发现，对于一阶振型，由于其模态形状并未发生改变，因此其频率也并无太大改变。而对其余三阶振型，弹性支撑使得其振型中的“半波”数目减少，即其弯曲形式发生明显变化，因此其频率将发生显著下降。这是因为根据Rayleigh原理，自振频率的平方等于势能与动能之比[16]。如果弹性支撑刚度的增加并未使得其模态振型发生显著变化，则其将仅通过略微减小动能而引起自振频率的增加。当刚度继续增加时，振型将会发生显著变化(主要表现为半波数目的增加)，此时由于势能的增加将会使得自振频率明显升高。

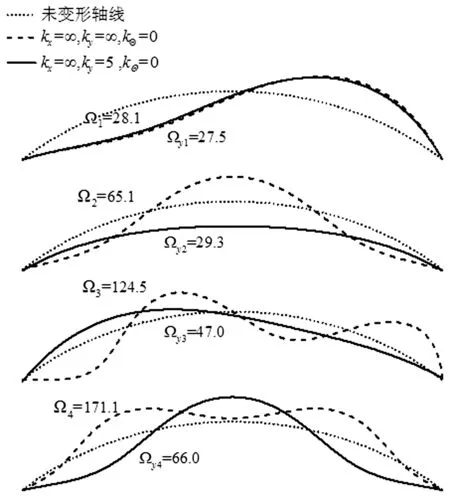
图6 竖向弹性支撑对振型影响Fig.6 The influence of the general boundary onto mode shapes

4.4 水平弹性支承对拱结构的频率影响

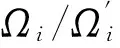
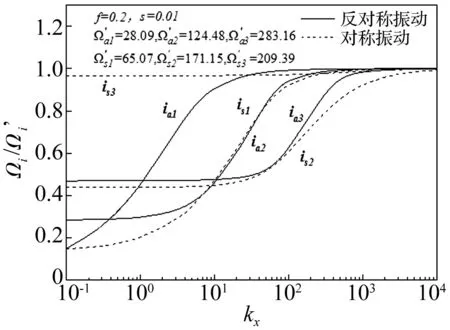
图7 水平方向弹性支承kx对频率比Ωi/Ω′i的影响Fig.7 Effects of kxon Ωi/Ω′i of horizontal elastic boundary conditions

4.5 竖向弹性支承对拱结构的频率影响

图8为f=0.2，s=0.01的双铰圆拱，竖直方向无量纲刚度ky对频率比Ωi/Ω′i的影响。其形状与规律同图7大致相同。但是对频率比Ωi/Ω′i有影响的ky值的范围将明显减小。

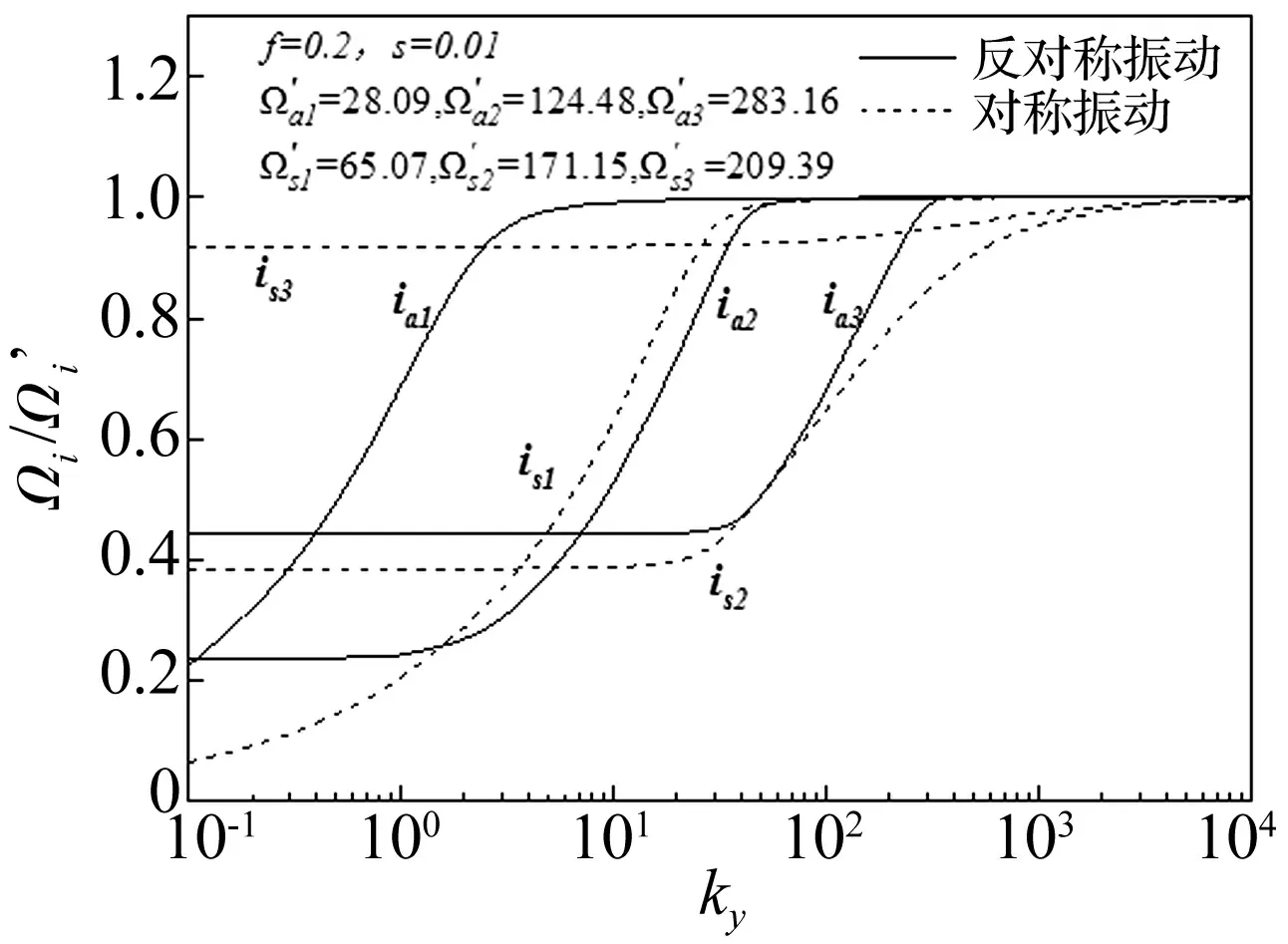
图8 竖直方向弹性支承ky对频率比Ωi/Ω′i的影响Fig.8 Effects of kyon Ωi/Ω′i of vertical elastic boundary conditon

为了进一步确定这种影响现象，通过计算矢跨比f从0.2～0.5，细长比s从0.1～0.001的圆拱的频率恢复曲线，其规律同图7、图8所示相同。在此范围内，弹性支座对于圆拱频率的影响随矢跨比f和细长比s的减小而增加，随频率阶数的升高而增加。这两种影响都可以归结为：弹性支座对圆拱频率的影响的增加随圆拱在理想支座情况下频率的升高而降低。

4.6 转动方向弹性支撑对拱结构的频率影响

图 9所示为转动方向弹性支撑对圆拱结构的自振频率的影响。kΘ由0到无穷，圆拱即由双铰拱过度到无铰拱。从中可以看出，与水平弹性支承与竖向弹性支承相比，转动方向弹性支撑的刚度只在很小的范围内影响拱结构的频率，且模态阶数越高，转动支撑的刚度对频率影响越弱。

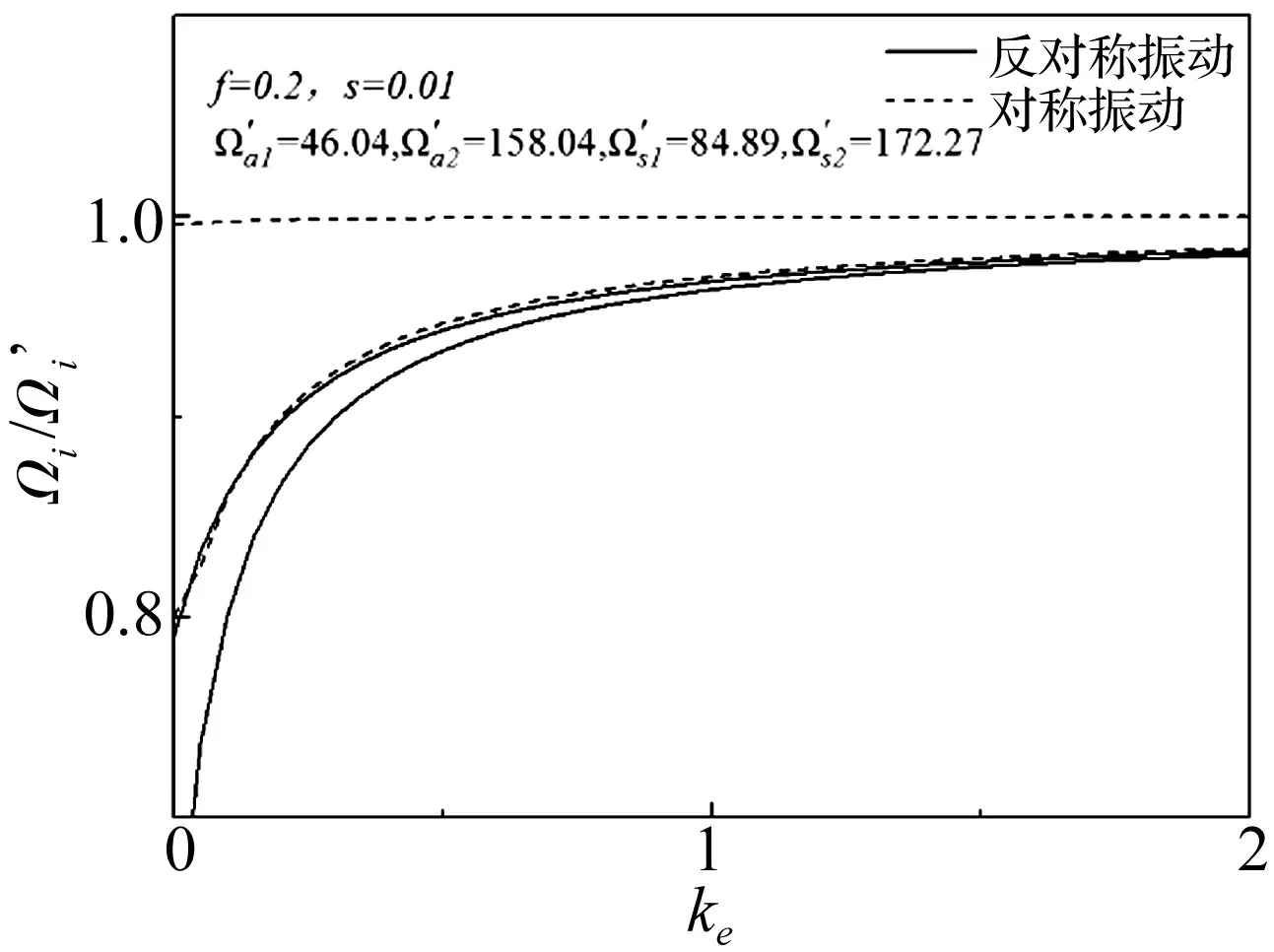
图9 转动方向弹性支承kΘ对频率比Ωi/Ω′i的影响Fig.8 Effects of kΘon Ωi/Ω′i of rotational elastic boundary conditon

5 结 论

本文通过将圆拱参数无量纲化，建立圆拱边界为竖直、水平和转动弹性支撑下的无量纲微分方程组和边界条件。并通过数值方法求解了圆拱的频率和振型随弹性支撑的变化所发生的变化。

(1) 在弹性支撑条件下，拱的基频由对称转换为非对称的临界矢跨比将会增大。

(2) 与理想边界情况相比，在弹性边界下，细长比s对Ωi的影响将大大减小。

(3) 对于不同矢跨比f、细长比s的拱的某一阶模态，水平和竖向弹性支承均只在某一范围内显著影响拱的Ωi。并且弹性支承对Ωi的影响范围和影响程度随矢跨比f和细长比s的减小、模态阶数的增大而减小。弹性支承的变化对Ωi的显著影响主要是使圆弧拱的振型发生了变化。

在忽略转动惯量的情况下，转动弹性支承仅在很小范围内对基频有显著影响，对高阶Ωi的影响较小。

[1] CHIDAMPARAM P, LEISSA A W. Vibrations of planar curved beams, rings, and arches[J]. Applied Mechanics Reviews, 1993, 46(9): 467-483.

[2] 项海帆. 拱结构的稳定与振动/高等结构力学丛书[M]. 北京：人民交通出版社, 1991.

[3] HENRYCH J. The dynamics of arches and frames[M]. Elsevier Scientific Pub. Co., 1981.

[4] 钱七虎，孙乃光, 陈震元,等. 拱型结构的自振频率计算及轴向变形对自振频率的影响[D]. 钱七虎院士论文选集, 1999.

[5] KARNOVSKY I A. Theory of arched structures[M]. New York, Ny: Springer New York, 2012.

[6] LEE B K, LEE J Y, CHOI K M, et al. Free vibrations of arches with general boundary condition[J]. KSCE Journal of Civil Engineering, 2002, 6(4): 469-474.

[7] 康婷, 白应生, 孙惠香. 水平弹性支撑圆拱的动力特性研究[J]. 力学与实践, 2013, 35(2): 50-55. KANG TING，BAI YING SHENG ,SUNHUIXIANG.Dynamic characteristics of the horizontal elastic support circular arch[J].Mechanics in Engineering,2013,35(2):50-55.

[8] WUNG S. Vibration of hinged circular arches[D]. Rice University, 1967.

[9] 张相，黄东才. 结构振动力学[M]. 上海：同济大学出版社, 1994.

[10] AL-KHAFAJI A W, TOOLEY J R. Numerical methods in engineering practice[M]. Holt, Rinehart And Winston, 1986.

[11] LEE B K, WILSON J F. Free vibrations of arches with variable curvature[J]. Journal of Sound and Vibration, 1990, 136(1): 75-89.

[12] LEE B K, LEE T E, AHN D S. Free vibrations of arches with inclusion of axial extension, shear deformation and rotatory inertia in cartesian coordinates[J]. KSCE Journal of Civil Engineering, 2004, 8(1): 43-48.

[13] CHIDAMPARAM P, LEISSA A W. Influence of centerline extensibility on the in-plane free vibrations of loaded circular arches[J]. Journal of Sound and Vibration, 1995, 183(5): 779-795.

[14] 金尼克. 拱的稳定性[M]. 上海：建筑工程出版社, 1958.

[15] FANNING P J, BOOTHBY T E, ROBERTS B J. Longitudinal and transverse effects in masonry arch assessment[J]. Construction and Building Materials, 2001, 15(1): 51-60.

[16] 克拉夫, 彭津. 结构动力学[M]. 北京：高等教育出版社, 2006.

Free vibration analysis of arches under elastic support boundary conditions

ZHAO Zhangyong1, QIU Yanyu1,2, WANG Mingyang1,2, SONG Chunming1,2, CAO Kan1

(1. State Key Laboratory of Disaster Prevention & Mitigation of Explosion & Impact, PLA University of Science and Technology, Nanjing 210007, China;2. School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

The boundary conditions of circular arches in practical engineering can not be always simplified as ideally hinged ends or fixed ones. In order to study the influences of elastic supports on the free vibration characteristics of circular arches, the variables, such as, forces and displacements were nondimensionalized. According to the balance equations and coordinate conversion, the boundary condition equations of arches with vertical, horizontal and rotational elastic supports were derived in polar coordinates. The flexural and axial deformations were considered while shear deformations and rotation inertias were neglected to establish the governing equations of motion of arches. The solutions to the governing equations of motion under the boundary conditions were the functions with respect to rise to span ratiof, slenderness s, and dimensionless stiffness matrix [K]. Runge-Kutta method and the determinant search method were used to solve the eigenvaluesΩiof the equations of motion and eigenvectors, i.e., modal shapes. Through calculating different configurations, it was shown that under the conditions of elastic supports, the effects of slenderness s on the arches’ natural frequencies are much smaller than those under the conditions of ideal supports; the effects of horizontal and vertical elastic supports on the natural frequencies decrease with increase in natural frequencies of arches under the conditions of ideal supports; the rotational elastic supports obviously influence the fundamental frequency of arches.

circular arch; free vibration; elastic support; modal shape; natural frequency; non-dimensionalization

2015-04-21 修改稿收到日期：2015-10-08

赵章泳 男，硕士生，1992年生

宋春明 男，博士生，副教授，1979年生

E-mail:ming1979@126.com

O327

A

10.13465/j.cnki.jvs.2016.21.018