一类带扰动的弹性梁方程正解的存在唯一性
2016-12-14鞠梦兰王文霞郝彩云
鞠梦兰,王文霞,郝彩云
(太原师范学院数学系,山西晋中030600)
一类带扰动的弹性梁方程正解的存在唯一性
鞠梦兰,王文霞,郝彩云
(太原师范学院数学系,山西晋中030600)
应用算子的不动点定理研究一类带扰动的弹性梁方程,获得了此类弹性梁方程边值问题正解的存在唯一性,并讨论了解对参数的连续依赖性.
弹性梁方程;正解;扰动;存在性唯一性;不动点定理
考虑如下带扰动的弹性梁方程边值问题

其中:λ∈(0,+∞)为参数;g为扰动项,g∈C([0,1],R+);f∈C([0,1]×R+,R+),R+=[0,+∞).称u(t)为问题(1)的正解,若u(t)>0,0<t<1,且满足方程(1)及其边界条件.
由于弹性梁方程的实际背景及其广泛的应用性,近年来对四阶边值问题的研究非常活跃,同时取得了大量的成果.对于梁方程正解的存在性问题,主要研究方法有上下解法[1]、压缩映射原理与单调迭代法[2]、Guo-Krasnosel′skii锥拉伸压缩不动点定理[3]、不动点指数法[4]、Leggett-Williams不动点定理[5]和Krein-Rutman定理[6].而关于带扰动的边值问题的研究尚不多见.文献[7]通过考察算子方程x=Ax+λBx,讨论了一类带扰动的两端简单支撑的弹性梁方程正解的存在性.文献[8]利用广义凹算子的不动点定理讨论了一类带扰动的三阶两点边值问题正解的存在性,但并未对解的相关性质进行讨论.从现有文献来看,关于正解存在唯一性的研究较少.本研究利用算子的不动点定理得到了方程(1)正解的存在唯一性,并讨论了解对参数的连续依赖性.
1 预备知识
设E为一个实Banach空间,θ为E中的零元素.
定义1[9]非空闭凸集P⊂E,称为E中的一个锥,若它满足
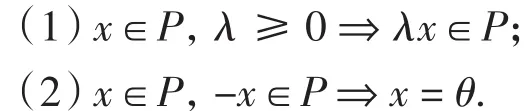
进一步,若存在常数N>0,使得∀x、y∈E,若θ≤x≤y,有‖x‖≤N‖y‖,则称P为正规锥,N称为P的正规常数.
由锥P可以在E中诱导半序如下:对x、y∈E,x≤y当且仅当y-x∈P.若x≤y且x≠y,则记为x<y.
定义2[10]设P是E中的锥,D⊂E,算子T:D→E称为递增的,若∀x、y∈D,当x≤y时,有Tx≤Ty.
定义3[10]称x*为算子T的不动点,若Tx*=x*.
给定e>θ,即e≥θ,且e≠θ,记

Pe={x∈E:存在与x有关的μ1(x)、μ2(x),

易知Pe⊂P.
定义4[11]称算子T:P→P为广义α-凹算子,若T满足
(1)T(Pe)⊂Pe;
(2)∀x∈Pe,∀r∈(0,1),存在α∈(0,1),使得T(rx)≥rαTx.
引理1[10,12-13]设 P是 E中的正规锥,算子 T:P→P为递增的广义α-凹算子,则有
(1)T在Pe中存在唯一不动点x*;

引理2[14]设P是E中的正规锥,x0∈Pe.算子T:为递增的,且∀x∈Pe,∀r∈(0,1),T(rx)≥rTx成立,则有

(2)当λ∈[λ*,+∞)时,算子方程x=x0+λTx在Pe中没有解;
(3)xλ关于λ是递增的,λ∈[0,λ*);
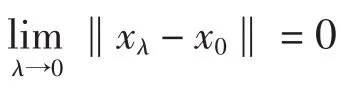
(5)当x≥x0时,Tx∈,且T是全连续的,则

记

2 主要结论
引理3[15]设y∈C[0,1],则边值问题

有唯一的解

其中

引理4 任取t0∈(0,1],则有

(1)0<t≤t0≤s≤1;(2)0<t≤s≤t0≤1;
(3)0<t0≤t≤s≤1;(4)0<s≤t≤t0≤1;
(5)0<t0≤s≤t≤1;(6)0<s≤t0≤t≤1.其中情况(1)~(4)的证明方法同文献[15]一致,只需将j(s)换成这里的t0即可.下面只需证明情况(5)和情况(6).
(5)当0<t0≤s≤t≤1时,有
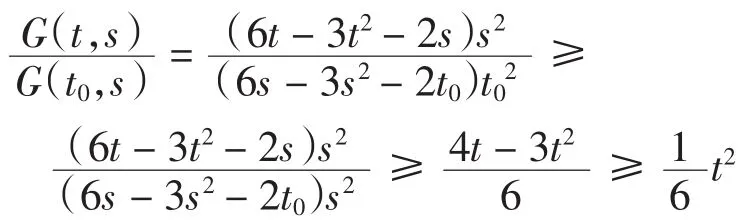
(6)当0<s≤t0≤t≤1时,有
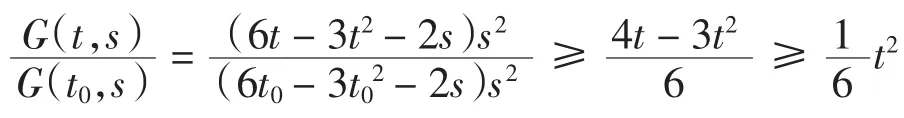
本研究对方程(1)做如下假设.
(H1)固定t∈[0,1],f(t,u)关于u∈[0,+∞)是递增的;
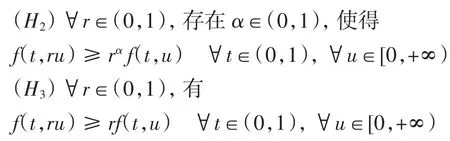
定理1 设(H1)与(H2)成立,g(t)>0,t∈[0,1],
则∀λ∈(0,+∞),方程(1)在Pe中存在唯一正解uλ(t),且解uλ(t)满足
(1)∀u0∈Pe,令

(2)对λ∈(0,+∞),uλ关于λ是递增的,且uλ≥x0;
(3)对每个λ∈(0,+∞),uλ关于λ是连续的;
其中

证明 (1)由引理3知方程(1)的解满足积分方程

其中:G(t,s)如式(4)定义,x0(t)如式(5)定义.对任意u∈P,定义T和Tλ
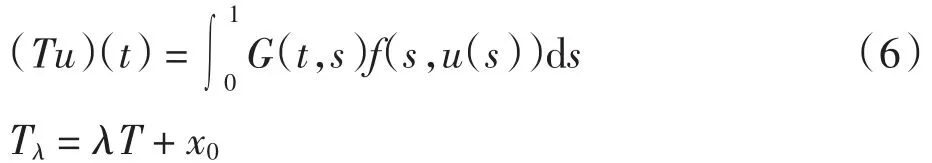
由G(t,s)≥0,g(t)>0,t、s∈[0,1],可得x0∈P.再由f(t,u)≥0,有(Tu)(t)≥0,t∈[0,1].于是T:P→P,且由(H1)可知T是单调递增的,从而Tλ:P→P,且Tλ也是递增的.下证Tλ是广义α-凹算子.
先证明Tλ:Pe→Pe.一方面,∀u∈Pe,有

另一方面,由(H2),∀t∈(0,1),以及∀u∈Pe与r∈(0,1),有
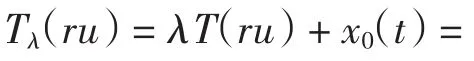
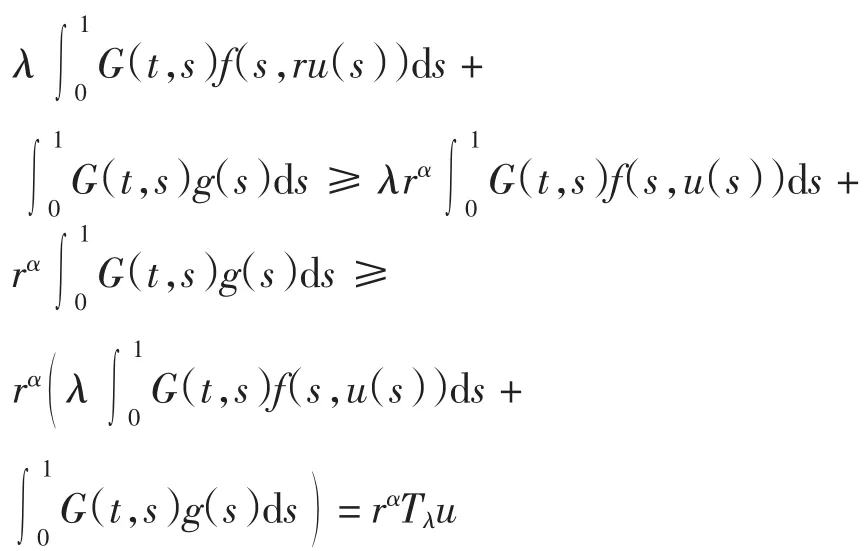
从而Tλ是一个广义α-凹算子,由引理1知Tλ在Pe中存在唯一正解uλ(t),且结论(1)成立.
(2)任取λ1、λ2∈(0,+∞),且λ1≤λ2,则由

由Tλ1的全连续性易知{xn}和{zn}分别一致收敛于x*和z*,且它们分别是Tλ1的最小不动点和最大不动点,从而有
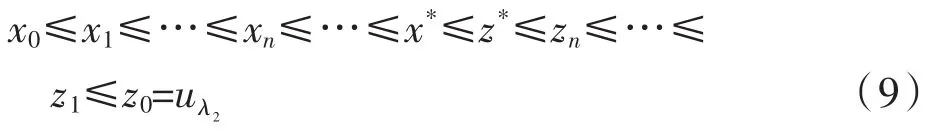
下证Tλ1在[x0,uλ2]上有唯一不动点.令

则有

由式(8)~式(11)有

断言ε=1.若不然,当n≥1时,有0<εn≤ε≤1,由Tλ1的α-凹性有

由式(10)有εn+1≥εαn,进而ε≥εα,这就产生了矛盾,故ε=1.
由式(9)和式(11)有

于是有x*=z*=uλ1是Tλ1在[x0,uλ2]中的唯一不动点,即uλ1≤uλ2.
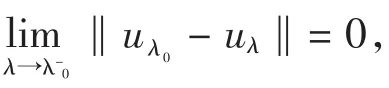
取序列{λn},使得
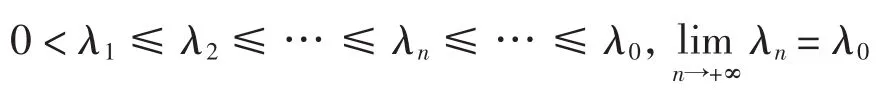
由结论(2)有

从而{uλn}在P中是有界的,即存在常数M>0,使得‖uλn‖≤M,n=1,2,….另外,由
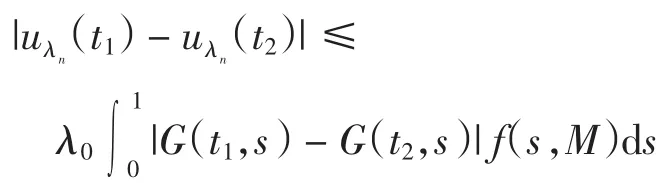
同理可证,∀λ0∈(0,+∞),当λ→λ0+时,有‖uλuλ0‖→0,即结论(3)成立.
类似于定理1的证明可得定理2.
定理 2 设(H1)与(H2)成立,f(t,0)>0,t∈[0,1],则∀λ∈(0,+∞),方程(1)有唯一正解uλ(t)∈Pe,且解uλ(t)满足
(1)∀u0∈Pe,令

(2)对λ∈(0,+∞),uλ关于λ是递增的,且uλ≥x0;
(3)对任意λ∈(0,+∞),uλ关于λ是连续的;
其中x0(t)如式(5)定义.
定理3 设(H1)与(H3)成立,g(t)>0,t∈[0,1],则存在λ*>0,使得∀λ∈(0,λ*),方程(1)有唯一正解uλ(t)∈Pe,对于λ∈[λ*,+∞),方程(1)无正解.解uλ(t)满足
(1)∀u0∈Pe,令
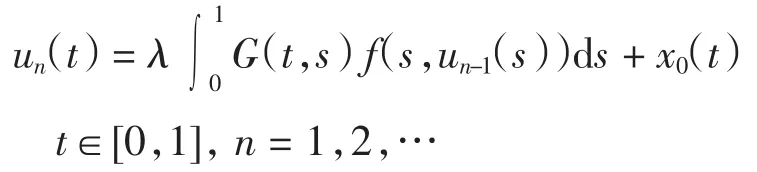
则un(t)一致收敛于uλ(t);
(2)uλ关于λ是递增的,λ∈(0,λ*);
(3)uλ关于λ是连续的,λ∈(0,λ*);
其中x0(t)如式(5)定义.
证明 由引理3知方程(1)的解满足
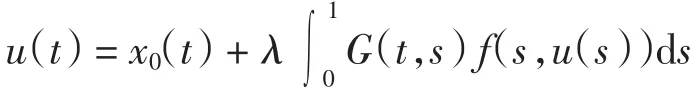
其中:G(t,s)如式(4)定义,x0(t)如式(5)定义.∀u∈P,算子T为

从而易知uλ为方程(1)的解等价于uλ为算子方程x= x0+λT的解.同定理1类似,可知x0(t)∈P,T:P→P为增算子.下证x0(t)∈Pe.
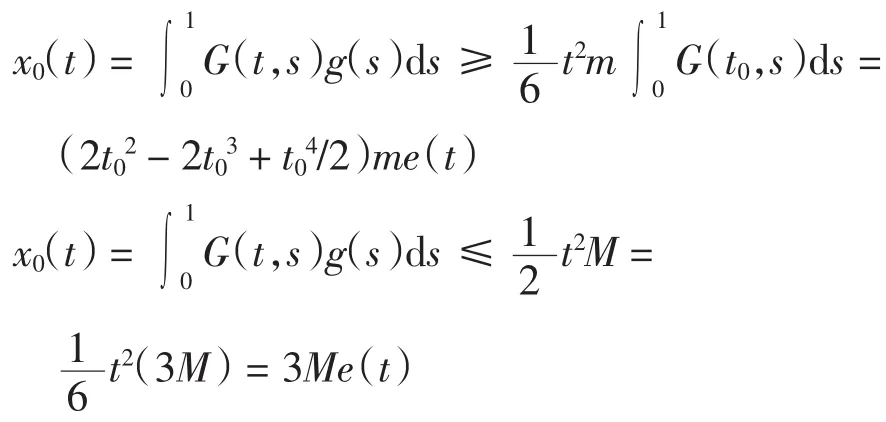
即x0(t)∈Pe.
下面证明T:Pe→.∀u∈Pe,由T的定义知Tu(t)≥0,且
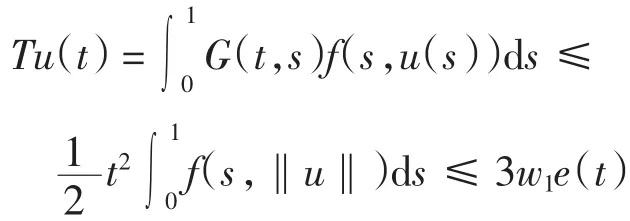
由(H3)知,∀t∈(0,1),∀u∈Pe及r∈(0,1),有
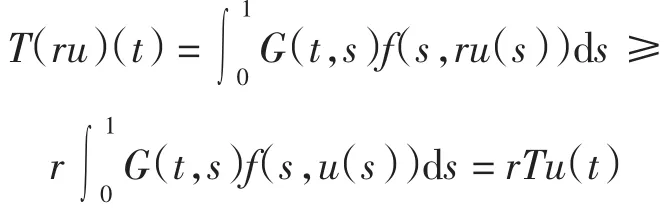
于是由引理2知定理结论成立.
[1] BAI Z B.The upper and lower solution method for some fourth-order boundary value problems[J].Nonlinear Analysis,2007,67:1704-1709.
[2]PEI M H,SUNG K C.Monotone iterative technique and symmetric positive solutions for a fourth-order boundary value problem[J].Mathematical and Computer Modeling,2010,51:1260-1267.
[3]WANG Q,GUO Y P,JI Y D.Positive solutions for fourth-order nonlinear differential equation with intergral boundary conditions[J].Discrete Dynamics in Nature and Society,2013,ID 684962,10 pages.
[4] 陆海霞,孙经先.一类四阶非线性微分方程两点边值问题的正解[J].数学的实践与认识,2014,44(8):229-235. LU H X,SUN J X.Positive solution of two-point boundary value problems for fourth-order nonlinear differential equation[J].Mathematics in Practice and Theory,2014,44(8):229-235(in Chinese).
[5] YANG Y R.Triple positive solutions of a class of fourth-order two-point boundary value problems[J].Applied Mathematics Letters,2010,23:366-370.
[6] MA R Y,XU L.Existence of positive solutions of a nonlinear fourthorder boundary value problem[J].Applied Mathematics Letters,2010,23:537-543.
[7] WANG W X,LIU X L.Positive solutions of operator equations and nonlinear beam equations with a perturbed loading force[J].Wseas Transactions on Mathematics,2012,11(3):252-261.
[8]杨晨,翟成波.带扰动和参数的三阶边值正解的存在唯一性[J].应用泛函分析学报,2013,15(3):272-275. YANG C,ZHAI C B.Existence-uniqueness of positive solutions for perturbed third-order boundary values with a parameter[J].Acta Analysis Functionalis Applicata,2013,15(3):272-275(in Chinese).
[9]郭大均.非线性泛函分析[M].第二版.济南:山东科学技术出版社,2001. GUO D J.Nonlinear Functional Analysis[M].2nd ed.Jinan:Shandong Science and Technology Press,2001(in Chinese).
[10]王文霞,梁展东.一类非线性算子的不动点定理及其应用[J].数学学报,2005,48(4):789-800. WANG W X,LIANG Z D.Fixed point theorems for a class of nonlinear operators and their applications[J].Acta Mathematica Sinica,2005,48(4):789-800(in Chinese).
[11]ZHAI C B,ANDERSON D R.A sum operator equation and applications tononlinearelasticbeamequationsandLane-Emden-Fowlerequations[J]. Journal of Mathematical Analysis and Applications,2011,375(2):388-400.
[12]ZHAO Z Q,DU X S.Fixed points of generalized e-concave(generalized e-convex)operators and their applications[J].Math Anal Appl,2007,334:1426-1438.
[13]ZHAI C B,YANG C,GUO C M.Positive solutions of operator equations on ordered Banach spaces applications[J].Comput Math Appl,2008,56:3150-3156.
[14]WANG W X,LIU X L,SHI P P.Nonlinear sum operator equations with a parameter and application to second-order three-point BVPs[J]. Abstract and Applied Analysis,2014,ID259016,9pages.
[15]鞠梦兰,王文霞,郝彩云.一类四阶两点边值问题正解的存在性[J].成都大学学报:自然科学版,2016,35(1):37-40. JU M L,WANG W X,HAO C Y.Existence of positive solution to fourth-order two-point boundary value problem[J].Journal of Chengdu University:Natural Science,2016,35(1):37-40(in Chinese).
(责任编校 马新光)
Existence and uniqueness of positive solutions for a kind of perturbed elastic beam equations
JU Menglan,WANG Wenxia,HAO Caiyun
(Department of Mathematics,Taiyuan Normal University,Jinzhong 030600,Shanxi Province,China)
By using the fixed point theorems for operators,the existence and uniqueness of positive solutions for boundary value problem of a kind of perturbed elastic beam equations are obtained.And the continuous dependence of the parameters is discussed.
elastic beam equations;positive solution;perturbation;existence and uniqueness;fixed point theorem
O177.91
A
1671-1114(2016)06-0005-05
2016-05-22
国家自然科学基金资助项目(11361047).
鞠梦兰(1991—),女,硕士研究生.
王文霞(1964—),女,教授,主要从事非线性算子及其应用方面的研究.
