带非线性阻尼项的等熵欧拉方程轴对称解的爆破
2016-12-14熊显萍黄激珊
熊显萍,黄激珊
(兴义民族师范学院数学科学学院,贵州兴义562400)
带非线性阻尼项的等熵欧拉方程轴对称解的爆破
熊显萍,黄激珊
(兴义民族师范学院数学科学学院,贵州兴义562400)
考虑三维空间中带非线性阻尼项的可压缩等熵欧拉方程组的初边值问题,研究其轴对称解的爆破.采用泛函方法,利用均值不等式及Schwartz不等式等对方程组的非线性阻尼项进行处理,证明了当初始速度足够大时,经典解在某一时间内必定爆破.
非线性阻尼项;等熵欧拉方程组;轴对称解;爆破
关于带阻尼项的可压缩欧拉方程组经典解的研究一直是相关领域内学者关注的热点问题[1-5].多数研究都是针对可压缩欧拉方程组 Cauchy问题或Dirichlet问题经典解的整体存在性和爆破问题进行讨论,其中关于经典解的整体存在性一般采用能量估计的方法,爆破问题的研究大多采用泛函方法,即在某些初始数据的泛函较大时[5],证明解必定在有限时间内爆破.文献[6]通过构造近似解以及对解与近似解的差进行估计,证明了解的爆破.文献[7]对文献[6]的方法进行了改进,采用了新的泛函研究外区域的等熵欧拉方程组初边值问题的经典解的爆破.文献[8]在对初始速度进行假设的基础上,研究了三维空间中带线性阻尼项的等熵欧拉方程组的经典解,证明了其经典解必定在有限时间内发生爆破.文献[9]利用平面动力系统分析的方法研究了一类特殊形式的解,证明了当初值落入平面上的某一区域时解会爆破,而落入另一些区域时则不会发生爆破.本研究考虑带非线性阻尼项的等熵欧拉方程组初边值问题的经典解,证明了当初始速度足够大时,经典解在某一时间内必定爆破.
考虑如下三维空间中带非线性阻尼项的等熵欧拉方程组的初边值问题

其边值条件为

其中:ρ、u、P分别为流体的密度、速度和压强;气体状态方程为P=Aργ,1<γ≤3;设非线性阻尼项f(u)为线性项和非线性项之和,即f(u)=αu+g(u),满足α为正常数,g(u)为光滑函数,且0<g(u)<α1(α1∈(0,n为单位球面上的单位外法向量.
本研究采用文献[8]的处理方法定义泛函,利用均值不等式及Schwartz不等式等对方程组的非线性阻尼项进行处理.考察初边值问题(1)~(2)的轴对称解,即解

将式(3)代入方程(1)~(2),则得对应方程组
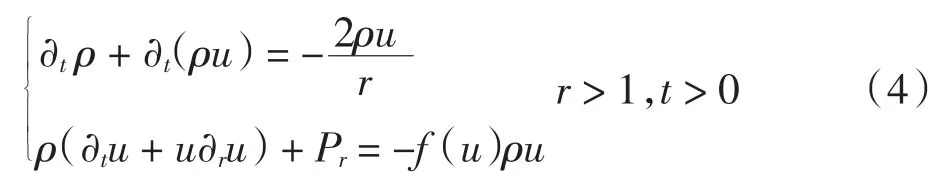
边值条件为

对于初边值问题(4)~(5),其初始条件为

引理1 假设(ρ,u)是初边值问题(4)~(6)的C(1[1,+∞)×[0,T))解,则当r≥R时,ρ(r,0)=,u(r,0)=0,且当r≥R+σt,t<T时,ρ(r,t)=,u(r,t)=0.
年轻人应该有正确的消费行为,这不仅仅是其作为未来社会主力的责任感,也是其成长过程中所需要的重要因素。从表面上看,正确的消费行为是一种举动,但是真正影响其消费行为的因素还是消费心理。目前在大学的课程中,并没有关于健康消费理念的教育,所以这实际上是缺失的。从经济影响角度看,形成正确的消费心理,这将让社会资源实现充分应用,同时也能够让这些资源实现经济价值的最大挖掘。特别是处于青春期的年轻人目前正是消费心理形成的重要阶段,所以培养其形成绿色消费等正确理念,也将会为整个社会的绿色经济发展提供一些帮助。
由引理1知,当r≥R+σt时,p(ρ(r,t))=p(ρ).以下记定义
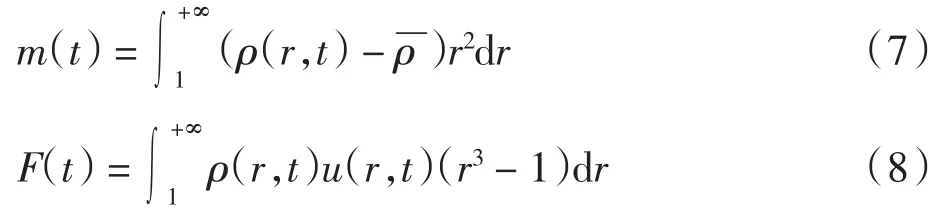
记A(t)=eα(tR+σt)2[m(0)+((R+σt)3-1)/3].由文献[7]可得引理2.
引理2 设(ρ,u)是初边值问题(4)~(6)在[1,+∞)× [0,T)上的C1解,则对所有0<t<T,有m(t)=m(0).
定理1 设(ρ,u)是初边值问题(4)~(6)在[1,+∞)× [0,τ),τ>0上的C1解.若m(0)≥0,且对任意T>0,有
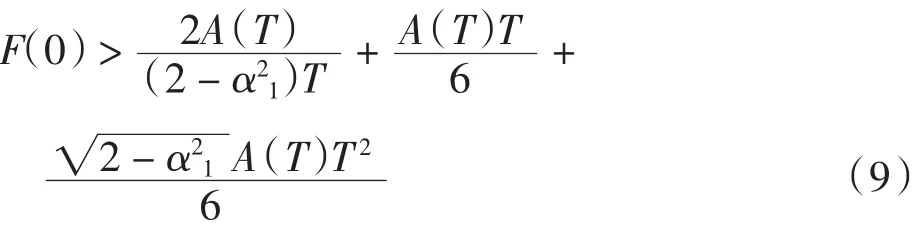
则τ<T.
证明 对式(8)两边关于t求导并由方程组(4)得
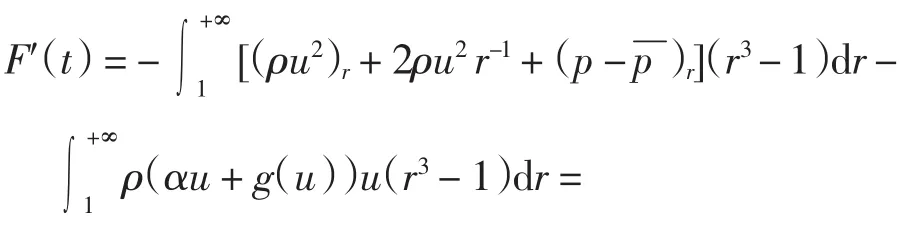


当m(0)≥0时,与不带阻尼项的情况一样,有
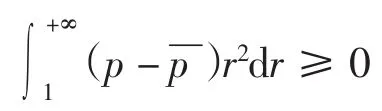
对ρug(u)(r3-1)利用均值不等式,有

因此可得

令G(t)=eαtF(t),因A(t)=eα(tR+σt)2[m(0)+((R+ σt)3-1)/3],故A(t)>0为单调递增函数,因此有

将式(12)在[0,τ]上积分,得

因为G(t)=eαtF(t),所以
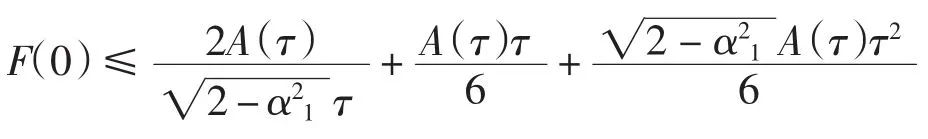
故必有τ<T,否则上式与式(9)矛盾.证毕.
对定理1中的不等式(12)重新处理,可得到如下定理.
定理2 设(ρ,u)是初边值问题(4)~(6)在[1,+∞)× [0,T)上的C1解.若对某一常数τ>0,有
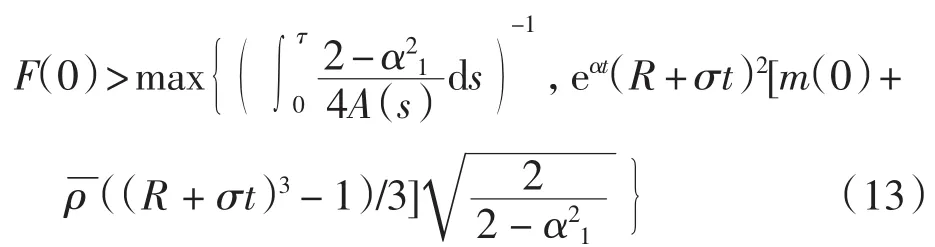
则T<τ.
证明 利用与定理1类似的处理方法可得
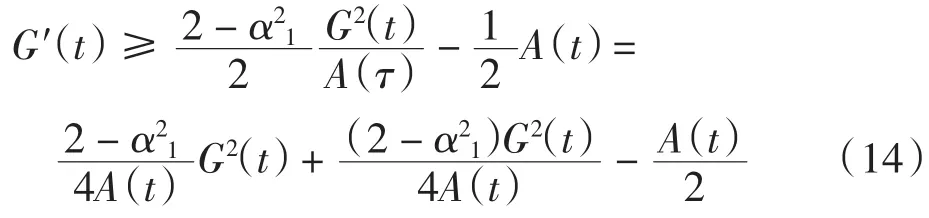

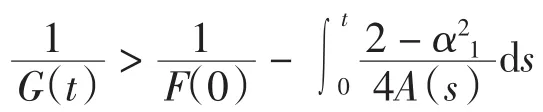
定理1和定理2的结果表明,虽然出现了非线性阻尼项,但当初始泛函足够大时,经典解必定不会整体存在.
[1]SIDERIS T,THOMASSES B,WANG D.Long time behavior of solutions to the 3D compressible Euler equations with damping[J].Comm Partial Diff Equns,2003,28:795-816.
[2] WANG W,YANG T.The pointwise estimates of solutions for Euler equations with damping in multi-dimensions[J].Journal of Differential Equations,2001,173:410-450.
[3] LIU Y Q,WANG W K.Well-posedness of the IBVP for 2-D Euler equations with damping[J].Journal of Differential Equations,2008,245(9):2477-2503.
[4] 朱长江,蒋咪娜.具有非线性阻尼项的P-方程组非线性扩散波的Lp-衰减率收敛率[J].中国科学:A辑,2006,36(3):262-280. ZHU C J,JIANG M N.Lpconvergence rate of nonlinear diffusion wave forP-equations with nonlinear damping[J].Science China:Ser A,2006,36(3):262-280(in Chinese).
[5]SIDERIST.Formationofsingularities in three-dimensional compressible fluids[J].Comm Math Phys,1985,101:475-485.
[6] YIN H,QIU Q.The blowup of solutions for 3D axisymmetric compressible Euler equations[J].Nagoya Math J,1999,154:157-169.
[7] ZHU X S,TU A H.Blowup of the axis-symmetric solutions for the IBVP of the isentropic Euler equations[J].Nonlinear Analysis:Theory,Methods and Applications,2014,95:99-106.
[8]朱旭生,俞银晶,李翠.带阻尼项的三维等熵可压缩欧拉方程组轴对称解的爆破[J].厦门大学学报:自然科学版,2014,53(6):780-784. ZHU X S,YU Y J,LI C.Blowup of the axis-symmetric solutions for the IBVP of the compressible isentropic Euler equations with damping[J]. Journal of Xiamen University:Natural Science,2014,53(6):780-784(in Chinese).
[9] LI T,WANG D.Blowup phenomena of solutions to the Euler equations for compressible fluid flow[J].Journal of Differential Equations,2006,221(1):91-101.
(责任编校 马新光)
Blowup of axis-symmetric solutions for initial-boundary value problem of compressible isentropic Euler equations with nonlinear damping
XIONG Xianping,HUANG Jishan
(School of Mathematical Sciences,Xingyi Normal University for Nationalities,Xingyi 562400,Guizhou Province,China)
The blowup of axis-symmetric solutions for the initial-boundary value problem of the compressible isentropic Euler equations with nonlinear damping in R3is investigated.By functional methods and managing the nonlinear damping using mean value inequality and Schwartz inequality,it is proved that the classical solutions will blow up before a certain time under the assumption that the functional associated with the initial velocity is sufficiently large.
nonlinear damping;isentropic Euler equations;axis-symmetric solutions;blowup
O175.4
A
1671-1114(2016)06-0010-03
2016-06-05
国家自然科学基金资助项目(11161021);贵州省教育厅自然科学基金资助项目(黔教科研发[2014]279号).
熊显萍(1978—),女,副教授,主要从事偏微分方程方面的研究.
