火箭发动机水下启动过程流场数值模拟研究

邹延兵,卓长飞,封 锋

(南京理工大学 机械工程学院,南京 210094)



火箭发动机水下启动过程流场数值模拟研究

邹延兵,卓长飞,封 锋

(南京理工大学 机械工程学院,南京 210094)

利用流体分析软件Fluent对水下火箭发动机启动过程流场进行了仿真。基于压力的求解器,采用了二维双精度解算器和轴对称理想水流场模型;时间采用一阶隐式离散;压力速度修正选用SIMPLE方法;多相流采用VOF模型;湍流模型采用K-epsilon模型,对处于50 m深水中的火箭发动机启动过程中喷管流场、尾流场进行了详细研究,分析了各参数的变化过程对喷管性能的影响。结果表明,对于给定的喷管,当喷管达到了超音速流动之后,马赫数都是确定的,当地的静压和总压成正比;水下火箭发动机轴向压力总体的变化趋势是在振荡中逐渐减少的,最后降低到环境压力;不同时刻轴线上温度的分布规律和速度基本相似。

水下火箭;流场仿真;尾流;气相发展

利用潜艇在水下发射火箭是一项先进的军事技术,它具有机动性、隐蔽性两大特点。目前,各军事大国都致力于该项技术的研究[1]。水下固体火箭发动机由于具有启动时间短、可靠性高、结构简单和航行速度快等优点,是许多主动攻击型水中兵器的首选动力。火箭水下点火的发射是一个复杂的过程。起初喷管是被堵住的,以防止外面的水进入燃烧室。火箭发动机水下点火,生成了高温高压气体,当燃烧室内压力超过了外界水压时,燃气将堵盖推开。发动机燃烧室内高温高压燃气经由喷管喷出,直接喷入水中[2-3]。在发动机点火瞬间,喷管内的气流场和喷管外的水流场物理变化非常迅速,气流中会出现复杂激波系的动态传播以及压力、温度等的不断变化,是一个涉及可压与不可压缩相的非稳态两相流动的工程问题。之后,通过快速的非定常流场变化,很快达到稳定的流场状态[4]。

国外对于这方面的研究大多以实验为主,并取得了一定的成果,理论分析特别是对水下火箭发动机启动过程流场的分析较少[5-6]。相比之下,国内对该问题的试验研究起步较晚,但是发展很快,多家单位建立了水下超音速射流实验装置[7-8];王诚等人[9]用一维非定常无粘可压缩模型,计算火箭水下发射腔内各物理量的分布变化情况以及燃气泡的演变过程,但其模型过于简单。

本文对处于50 m深水中的火箭发动机启动过程中的喷管流场、尾流场进行了详细研究,并分析该发动机的气相发展、压力、速度、温度的变化过程。研究结果为水下火箭发动机的设计提供依据和参考。

1 数学与物理模型

本文计算做如下假设:①忽略相与相之间的传质,以及各相与喷管之间的导热;②不考虑液体的表面张力;③将水看作是不可压的流体;④忽略重力,将射流气体当做理想气体考虑;⑤不考虑来流,火箭处于静水中。

火箭发动机喷管的基本型面尺寸如图1所示。

图1 喷管型面基本尺寸

为了与实际情况符合得更好,需要在一个很大的空间来模拟一个无限大的水域,使得流场的计算不受到计算区域大小的影响。计算区域的长度大于整个喷管长的10倍,为1.9 m,宽度为发动机半径的10倍,为0.75 m,如图2所示。

本文在Fluent软件平台上进行计算,基于压力的求解器,采用二维双精度解算器和轴对称模型,时间采用一阶隐式离散,压力速度修正选用SIMPLE方法;多相流模型采用VOF模型,多相介质采用理想气体和液态水,并定义气体为第一相(气相),水为第二相(液相);湍流模型采用k-epsilon模型。

图2 计算域网格

边界条件的确定:首先,喷管入口(即燃烧室末端)处选择压力入口,定义总压和总温。定义喷管边界和导弹尾部外壳为墙边界,其他的流场边界都定义为压力出口。喷管入口的压力和温度采用线性规律,在0.015 s内从环境压力(pa随深度不同而不同)和环境温度分别增大到10 MPa和3 500 K,之后温度、压力保持不变,即

式中:p为入口总压,Pa;T为入口总温,K;t为发动机工作时间,s;pa为环境压力,Pa。

在喷管内部设置了3个监控点,分别位于喷管喉部、扩张段中部和喷管出口截面,用于监视喷管扩张段的压力变化。采用这些数据一方面可以判断计算是否收敛,另外也可以观察喷管扩张段内流动参数的变化规律。

流场的初始化:整个流场0s时两相速度均为0,两相压力为水深相对应的环境压力(本文计算假设火箭发动机置于50m的水深中),温度为环境温度300K,初始化喷管内充满气体,压力与喷管外水的压力一致,外界水不能进入喷管内,喷管外全部为水。

2 计算结果与分析

2.1 气相发展过程

图3给出了主要时刻气相流场(气相体积分数云图)的发展过程。可以看出,初始时刻喷管内充满气体,喷管外充满水。喷管入口压力线性增大的起点是环境气压,也就是说一开始喷管与外界的压力差比较小。这个逐渐增大的压力差缓慢地推动外界的水运动。t=3.0ms时刻,运动的气体在喷管出口处冲击到水上,受到了水的阻挡,在出口处形成了一个滞止区。气体在轴向受到的阻力要大于径向的阻力,气体速度向外偏转,产生了径向的速度。在喷管边缘气相快速地往外生长,径向的生长速度大于轴向的生长速度。t=5.0ms时刻,气相区域逐渐增大,气泡将喷管出口和导弹尾部完全包裹住。

从图中6.8～15.9ms可以看出,这个时候气泡的运动主要表现在轴线方向,气泡不断伸长。从15.9～25.6ms这9.7ms内水流往前运动很大一段距离,喷管后部一束很细的水流几乎要将气泡切开。水在运动到主流附近时又会随着主流方向运动。这部分水运动在主流和回流之间,将主流和回流分开。喷管外的水并不能运动到很靠近轴线的位置,而是在主流的边界随着主流运动。反向运动的气体最终被沿着主流运动的水切断。气体的主流在水的作用下最后只能在一个略小于喷管出口的通道中运动,气相在主流边界运动时还会形成小的漩涡。气相与液相之间表现为强烈的湍流现象,边界处出现漩涡。气水交界面起伏跳动着,像是波浪一样往后传递。水一旦靠近轴线,造成了气相流动的通道减少。那么在这个减少的通道之前气体压力会增大,使得流进气相中间的水又远离轴线,与此同时插进气相中的水流还在以很快的速度往后运动。气水交界面后期的流动几乎是在重复这一过程。另外,从轴线方向来看,在喷管附近的气水交界面上的较小振荡在往后流动的过程中不断地放大。还可以观察到,离喷管较近的地方气水交界面差不多还是较小起伏的波浪形,远离喷管波浪的起伏变大,甚至水流会穿插到主流和气相的“波峰”之间,切断“波峰”。由以上分析可知,水下火箭发动机启动过程中,燃气与水强烈耦合,流场异常复杂。

图3 流场气相发展过程(气相体积分数云图)

2.2 流场压力变化规律

图4给出了喷管内3个监控点的压力随时间的变化曲线。图5给出了喷管内不同时刻马赫数等值线图。从图4可以看出,发动机启动过程中在喷管内还未建立起超音速流场时,整个喷管内为亚音速流动,3个监控点的压力随着燃烧室压力的增大均不断增大。由图5看出,随着时间推移,喷管喉部附近内开始出现超声速流动,随之产生的还有激波,并不断靠近喷管出口,气体通过激波后压力必将下降。这个现象也可以从图4中清楚地看到。当激波移动到喷管出口附近并保持位置不变后,从图4中看到3个监控点的压力开始线性增加,这是由喷管入口压力线性增加导致的。对于给定的喷管,当喷管达到了超音速流动之后每个地方的马赫数都是确定的,当地的静压就和总压成正比。激波运动到喷管以外后,喷管内的流动为稳定的超音速流动,各种参数不再改变。这个结论可以由3个监控点压力在t=15 ms以后不再改变看出,说明在t=15 ms以后喷管内流动已经稳定。

图4 各监测点处压力随时间的变化曲线

图5 不同时刻喷管内马赫数等值线图

图6给出了不同时刻压力等值线与水气交界面位置图。由计算结果可以看到,随着燃烧室压力不断增大,在喷管内部逐渐形成了超音速气流。在超音速气流形成的过程中喷管扩张段内出现了激波。激波在燃烧室压力的推动下由喷管喉部向喷管出口运动。但是由于外界是水,其惯性相当大,气体在向外运动的过程中受到了阻滞,于是在喷管出口处形成了一个高压区。这个高压区推动水往后运动,而气体又不断地冲击着气水交界面使得这个高压区不断追随着气水交界面向后运动,远离喷管。由图可以看到,高压区在轴线与气水交界面处。到了流动的后期,高压区离喷管出口越来越远。气体射流在充分膨胀后由于粘性速度逐渐降低,动能减少,到达水气交界面的滞止压力也就随着水气交界面的远离而减小了。最后高压区也渐渐消失了。

图6 不同时刻压力等值线和水气交界面位置图(单位:Pa)

图7给出了不同时刻流场中心轴线上压力的分布图。

图7 不同时刻流场中心轴线上压力分布图

图7中在15 ms时喷管入口压力增大到了最大值。各时刻0～0.2 m处的压力已不随时间变化,激波已经完全冲出喷管(0～0.18 m范围内),喷管内为稳定的超音速流动。轴线上第一道激波最后稳定在0.22 m附近,从图中可以清楚看到,各时刻压力在该位置突然增大。

从图5可以看到,这是喷管出口外的一道斜激波,在这道激波后流场变化得很剧烈。在水的作用下,气体在一个比喷管出口略小的通道中运动。这中间会出现激波的反射。复杂的波系使得流场的压力剧烈地跳动着,直到越过了水气交界面,压力开始逐渐下降并趋于环境压力。压力波在这个通道中往后传播,这表现在整个尾流场的压力在沿着轴线方向上波动。

图8(a)、图8(b)为流场中心轴线上不同位置处压力随时间的变化曲线。可以看到,喷管出口外的第一道斜激波的位置在不断变化,主要表现为与轴线的夹角在不断变化。这说明在水流的作用下,气体射流的通道直径在不断变化,喷管附近通道变小,压力变大,斜激波往喷管方向后退,而通道变大的时候压力减小,斜激波又往外运动。这使得斜激波运动过的区域的流动参数变化非常剧烈。斜激波来回的运动就好像是一个振荡源。这个振荡对后面的流场造成了很大的影响。在喷管后面的流场中,这个振荡在空间尺度上被不断地放大,最终形成了后面的复杂流场。

图8 流场中心轴线上不同位置处压力随时间的变化曲线

图9为t=67.08 ms流场轴线上压力分布曲线。经过细致的观察发现,虽然气体通道界面的改变很小,但是压力值跳动很厉害。这一点可以从图8(a)看到。压力变化最大的时候从1.6 MPa突然下降到0.8 MPa。从图8(a)和图8(b)的对比可以发现,在x=0.50 m处的压力跳动比x=0.25 m处幅值有所减少,但是跳动的频率明显增大。轴向上的压力总体的变化趋势是在振荡中逐渐减少的,最后降低到环境压力,这结论可以从图9中逐渐衰减的波动曲线得出。

图9 t=67.08 ms时流场轴线上压力分布曲线

2.3 流场马赫数变化规律

图10给出了不同时刻喷管中心轴线上马赫数变化曲线。从图中可以得出喷管内建立超音速过程中轴线上马赫数的变化规律。喷管内起初为亚音速流动,然后形成局部超音速,喷管内产生激波。随着燃烧室压力的增大,激波逐渐被推出喷管,喷管内部形成了稳定的流动。对比相关文献可以知道[7-8],本文得到的喷管内部的流动与文献中得到的结论是一致的,这也验证了本文计算的可靠性。

图10 不同时刻喷管中心轴线上马赫数变化曲线

图11给出了不同时刻喷管内及出口附近流场马赫数等值线图。发动机工作初期,喷管内形成一道激波,激波运动到喷管出口附近稳定下来,形成一道斜激波。t=6.5 ms时,高温气体射流在喷管出口附近形成了马赫盘,马赫盘之后压力较高,流动为亚音速,气流在此高压区作用下又做加速运动,然后又在后面的高压区的影响下减速或者是偏转反向形成反向射流;而马赫盘之前是超音速气流,压力较低。t=8.6 ms时,马赫盘减弱并消失。t=34.58 ms时,马赫盘消失,喷管出口附近的斜激波在中心轴线和水气交界面上多次反射,形成X激波。

图12给出了不同时刻流场中心轴线上马赫数曲线图。高温气体在运动到气水交界面附近时会通过一道强大的马赫盘,速度急剧降低到一个很低的值,最后减速到0。随着气水交界面远离喷管出口,气相运动的空间逐渐增大,轴线上的速度变化越来越剧烈,气相部分中出现的波系也一直在增加。波系的交错和在气水交界面的反射使得流动变得非常复杂。

图11 不同时刻喷管内及出口附近流场马赫数等值线图

2.4 流场温度变化规律

图13给出了不同时刻流场中心轴线上温度变化曲线。

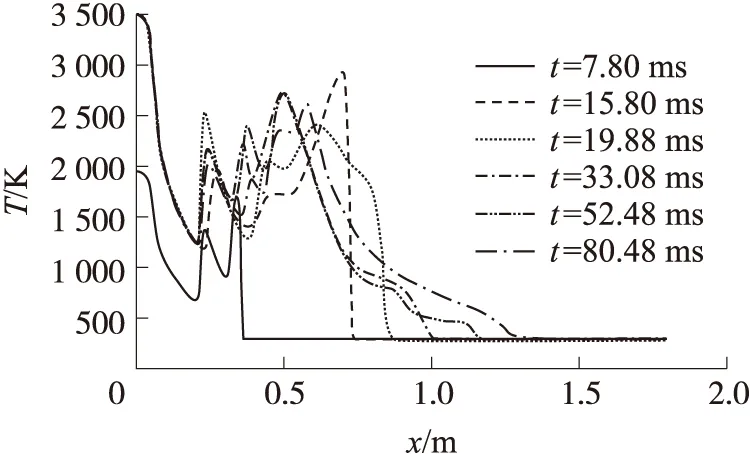
图13 不同时刻流场中心轴线上温度变化曲线

由图13可以看出,温度的分布规律和速度基本相近。喷管出口附近的激波之前的温度是稳定值,在经过斜激波之后温度开始震荡,这种变化仍然是由于复杂的波系的作用。在流场存在着很多激波,这些激波交错并在水气交界面上反射,在沿着轴向方向上还不断来回运动着。复杂激波的叠加和运动使得流场的温度处于跳动的状态,这一点和压力、马赫数变化规律中讨论的一样,是由于整个流场随时间在不断震荡导致的。这种振荡并没有表现出周期性,随机的振荡使得流场更加复杂。

4 结束语

本文利用流体分析软件Fluent对水下火箭发动机启动过程流场进行了仿真。对处于50 m深水中的火箭发动机启动过程中喷管流场、尾流场进行了详细研究,通过分析气相发展、压力、速度、温度的变化过程,得出以下几点结论:

①水下火箭发动机启动过程中,燃气与水强烈耦合,气水交界面起伏不断。离喷管较近的地方气水交界面差不多还是较小起伏的波浪形,远离喷管波浪的起伏变大,甚至水流会穿插到主流和气相的“波峰”之间,切断“波峰”,造成流场异常复杂。

②对于给定的喷管,当喷管达到了超音速流动之后每个地方的马赫数都是确定的,当地的静压就和总压成正比。激波运动到喷管以外后,喷管内的流动为稳定的超音速流动,各种参数不再改变。

③水下火箭发动机轴向上的压力总体的变化趋势是在振荡中逐渐减少的,最后降低到环境压力。

④随着气水交界面远离喷管出口,气相运动的空间逐渐增大,轴线上的速度变化越来越剧烈,气相部分中出现的波系也一直在增加。波系的交错和在气水交界面的反射使得流动变得非常复杂。

⑤不同时刻轴线上温度的分布规律和速度基本相近。喷管出口附近的激波之前的温度是稳定值,在经过斜激波之后温度开始震荡,这种变化仍然是由于复杂波系作用的结果。

[1] 仲峰泉,陆夕云,庄礼贤.火箭水下发射复杂流场的近似数值模拟[J].宇航学报,2000,21(2):1-7. ZHONG Feng-quan,LU Xi-yun,ZHUANG Li-xian.Numerical simulation of the complex flow field for rocket launch under water[J].Journal of Astronautics,2000,21(2):1-7.(in Chinese)[2] 王建儒,赵仕厂.水下固体火箭发动机尾流场计算[J].固体火箭技术,2007,30(5):388-391. WANG Jian-ru,ZHAO Shi-chang.Computations for solid rocket moter tail flow under water[J].Journal of Solid Rocket Technology,2007,30(5):388-391.(in Chinese)

[3]王晓宏.导弹水下发射时喷管的气体流动[J].推进技术,2001,22(1):61-64. WANG Xiao-hong.Nozzle flows of the missile launching under water[J].Journal of Propulsion Technology,2001,22(1):61-64.(in Chinese)

[4]徐小强.水下燃气喷管高速射流问题研究[D].杭州:浙江大学,2004. XU Xiao-qiang.Research on high-speed gas jet of nozzle underwater[D].Hangzhou:Zhejiang University,2004.(in Chinese)

[5]LINDAU J W.Multiphase computations for underwater propulsive flows,AIAA 2003-4105[R].2003.

[6]LINDAU J W.Computation of compressible multiphase flows,AIAA 2003-4105[R].2003.

[7]张帅.大深度水下固体火箭发动机发动机工作特性研究[D].南京:南京理工大学,2012. ZHANG Shuai.Reaserch on the character of solid rocket motor working deep underwater[D].Nanjing:Nanjing University of Science and Technology,2012.(in Chinese)

[8]向敏,吴雄,张为华,等.水下固体发动机尾流场数值仿真[J].推进技术,2009,30(4):479-483. XIANG Min,WU Xiong,ZHANG Wei-hua,et al.Numerical simulation for underwater solid moter tail flow[J].Journal of Propulsion Technology,2009,30(4):479-483.(in Chinese)

[9]王诚,叶曲源,何有声.火箭水下发射燃气泡的计算[J].应用力学学报,1997,14(3):1-8. WANG Cheng,YE Qu-yuan,HE You-sheng.Calculation of an exhausted gas cavity behind an under-water launched missile[J].Chinese Journal of Applied Mechanics,1997,14(3):1-8.(in Chinese)

Numerical Simulation of Flow Field for Underwater Starting Process of Rocket Engine

ZOU Yan-bing,ZHUO Chang-fei,FENG Feng

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

The underwater starting process of rocket engine was simulated by fluid analysis software Fluent.Two-dimensional double-precision solver,pressure solver and ideal axisymmetric water-flow-field model were used.First-order implicit time discretization was used,and SIMPLE was used in pressure velocity correction method.The VOF model was used to study Multiphase flow,and K-epsilon model was used in turbulence model.Noozle flow field and wake field of the underwater rocket engine working in 50 m deep water were researched in detail,and the effects of change process of parameters on nozzle performance were analyzed.For a given nozzle,Mach number is determined for each place when the nozzle reaches supersonic flow,and the local static pressure is proportional to total pressure.Overall trends of the axial pressure in the underwater rocket engine gradually reduces in the oscillation,and finally down to ambient pressure.Distribution of temperature on axis at different times is substantially similar to temperature.

underwater rocket;flow field simulation;wake;development of gas phase

2016-06-06

邹延兵(1991- ),男,硕士研究生,研究方向为航空宇航推进理论与工程。E-mail:zybadj@163.com。

V435.11

A

1004-499X(2016)04-0030-06