火炮制退机关键结构尺寸及公差优化研究

李 荣,杨国来,刘 宁,葛建立

(南京理工大学 机械工程学院,南京 210094)



火炮制退机关键结构尺寸及公差优化研究

李 荣,杨国来,刘 宁,葛建立

(南京理工大学 机械工程学院,南京 210094)

为探索名义尺寸和公差不能同步优化导致的火炮制退机设计周期长的问题，进行了制退机关键结构尺寸及公差的优化研究，改进了计及公差的区间优化方法。假设公差服从正态分布，构建了基于离散化的区间可能度模型，改进了公差指标，建立了火炮制退机关键结构尺寸及公差的区间优化模型。与传统火炮制退机结构参数优化结果进行了对比，优化得到了制退机关键尺寸的公差，缩短了制退机的设计周期。结果表明，采用基于离散化的区间可能度模型能得到目标性能更优的Pareto最优解，改进的公差指标能更好地反映平均公差和加工精度的关系。

火炮;制退机;区间可能度;公差等级系数;尺寸优化

传统火炮制退机结构参数优化设计是基于确定性模型得到结构参数的确定值[1],设计人员再根据加工条件、装配要求等对确定值进行公差设计,若在加工和装配中发现工序公差无法实现,工艺人员需将结果反馈给设计人员重新进行公差分配。因此,名义尺寸和公差不能同步优化设计导致了设计周期加长,成本增加。同时,不确定的尺寸会影响优化的目标性能或改变约束的可行性,因此需要研究结构优化中的尺寸不确定性问题。

研究不确定性问题一般基于概率模型和非概率模型。概率模型需得到参数精准的概率分布，而非概率模型只需参数上下限。然而在实际工程中更多使用和更易获得的是参数上下限,因此研究尺寸参数的区间不确定优化很有工程意义。王冲[2]基于区间理论建立了含有非概率不确定参数的区间有限元分析方法及区间鲁棒优化模型,结构-声场耦合系统鲁棒优化结果表明了该模型的有效性。石海军[3]考虑工程设计中关键尺寸或材料参数变化的区间,将目标和约束性能退化估计作为原优化问题的附加约束,形成内外层优化结构,有效解决了具有参数区间不确定的某火炮协调器优化问题。Jiang C[4]定义了公差指标,通过基于可靠度的区间可能度模型提出了考虑公差的区间优化方法,同时优化得到了名义尺寸和公差,通过3个算例表明了该方法的正确性,但局限于以区间中点的目标值研究整个区间的目标性能。

针对火炮制退机关键结构参数的名义尺寸和公差不能同步优化的问题,仅考虑公差对尺寸不确定性的影响,通过改进文献[4]的计及公差的区间优化方法,并在传统火炮制退机结构参数优化基础上,以制退筒内径和制退杆外径的尺寸和公差为设计变量,以原目标性能的区间和加工精度为目标,建立了火炮制退机关键结构尺寸及公差的区间优化模型,实现了制退机的关键结构参数的名义尺寸和公差的同步优化。

1 基于离散化的区间可能度

为将不确定性优化问题转化为确定性优化问题,本文基于离散型随机变量表征设计参数的区间,提出了一种基于离散化的区间可能度模型(Discretization-based Possibility Degree of Interval,DPDI)。

1.1 公差的正态分布假设

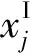
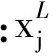
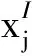
(1)

式中:Φ(x)是μ=0且σ=1的标准正态分布的分布函数。

1.2 区间数及其函数的离散化

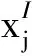
(2)

式中:j∈M,k∈N。式(2)的概率公式仅与n和k有关,在给定其取值水平个数n后p(xj)为n个常值。

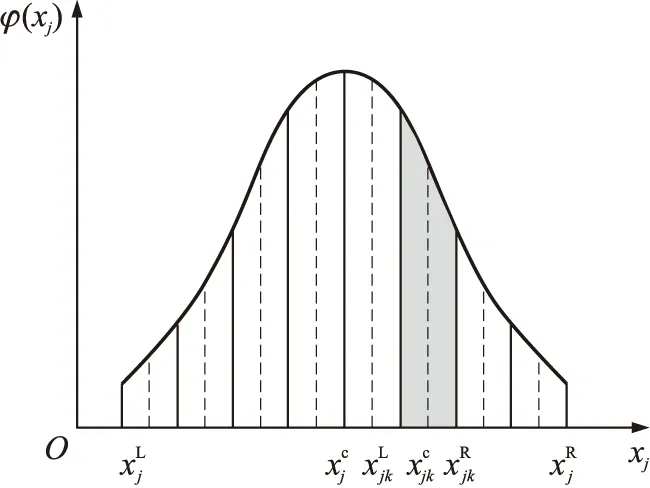
图1 区间数离散化示意图

(3)

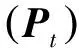
1.3 基于离散化的区间可能度模型

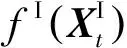
(4)

式中:t,z∈Q;k1,k2,…,km,h1,h2,…,hm∈N。

(5)

式中:t,z∈Q;k1,k2,…,km,h1,h2,…,hm∈N。

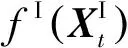
(6)

2 改进的区间优化模型

2.1 公差的区间对称描述

(7)

(8)

法国农业部正在采取行动，要求农药零售商向农民提供36种杀虫剂替代品，以鼓励更环保的做法。例如，经销商不会仅仅只兜售杀虫剂，可能同时还会推荐某种间种作物，或者推荐使用性信息素诱捕器来迷惑雄性昆虫，干扰害虫的繁殖等来杀死害虫。农业部给他们定下的目标是到2021年减少20%的农药用量，达不到目标的经销商将面临处罚。

2.2 构建新的确定性目标函数

标准公差IT基本上是由公差等级系数a和公差单位i的乘积来确定,它不随公差带位置改变[8]。公差单位i的计算公式为

式中:D为直径,i和D的单位均为mm。

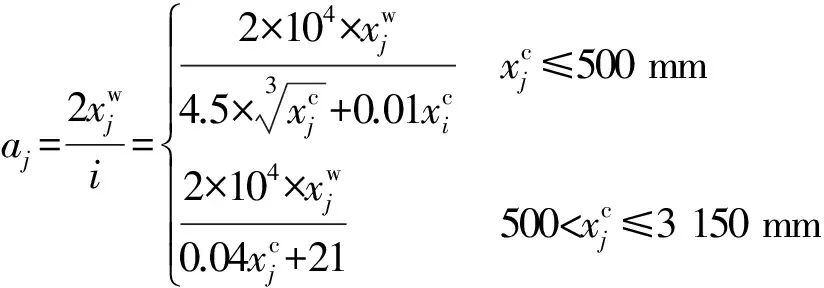
(9)

aj对应无量纲公差等级系数,aj越小,加工精度越高。公差等级系数采用优先数得到,而优先数是等比数列导出,因此采用几何平均数来构建公差指标A:

(10)

式中:A为平均的公差等级系数,它综合反映了所有尺寸的平均公差大小,A越大表示整体公差越大。

2.3 改进的计及公差的区间优化模型

一般的优化问题通过本文所提的DPDI和改进的公差指标A转化为确定性优化问题,由于一般的优化问题求最小值,故在平均公差等级系数前加负号。改进后的计及公差的区间优化模型为

(11)

式中:β=1,2,…,l,l为约束函数个数。本文采用罚函数法将上述有约束优化问题转化为无约束优化问题,以便编程计算。

3 优化实例

3.1 解析函数对比算例

以文献[4]中的解析函数为对比算例,计算含有2个设计参数的优化问题,根据式(11),n取10,解析函数优化问题转化为如下形式:

(12)

采用NSGA-Ⅱ遗传算法编程计算。解析函数对比算例的确定性最优解为x1=22.389,x2=12.504,f=127.406。文献[4]的结果为改进前,本文区间优化结果为改进后,选取改进前和改进后最优Pareto解集的一部分列入表1,对比分析。

改进前优化结果目标性能最优为134,改进后最优目标性能区间为[127.7,128],表明考虑目标性能区间分布使得优化结果在目标性能上更优;改进前第1组设计方案W为0.020 8,其本身没有对应工程意义,改进后第1组设计方案A为30.83,对应的公差等级IT在8级～9级之间,A很好地反映了参数的平均公差大小和具体加工精度的关系,A越大,平均加工精度越低,这使得A的工程实际意义明确对应平均加工精度;图2为解析函数算例的Pareto最优解集,图2反映了目标性能的最优区间会随着A的增大而逐渐变差,两者成负相关。

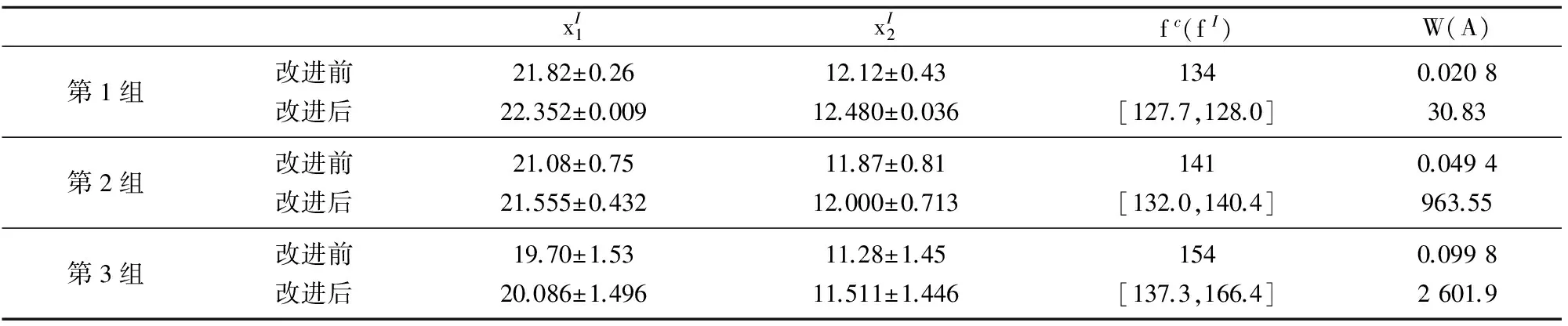
表1 改进前后优化结果对比

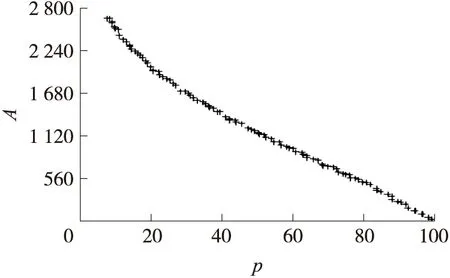
图2 解析函数算例的Pareto最优解集

3.2 火炮制退机关键结构尺寸及公差优化

基于第1节和第2节改进方法的研究和第3.1节的验证,在文献[9]的火炮制退机结构参数优化模型的基础上,建立火炮制退机关键结构尺寸及公差的区间优化模型。

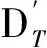
根据式(11),同时n取10,优化问题转化为

(13)

式中:E为自由后坐能量,λmax为最大后坐长度,e为考虑装配误差及射击条件保留的余量,dp为节制环内径，d1为制退杆内径,hm为复进节制器沟槽最大深度,[σ]为制退杆材料许用应力,ns为安全系数,λjx为极限后坐长,Ffmax为复进节制器最大液压阻力;K为与杆两端固定情况有关的系数,节制杆视为一端固定一端铰接,K=2π2;Es为节制杆材料弹性模量;Sx,max为流液孔面积最大值。

以某火炮制退机为例,区间优化和确定性优化均从结构初始值开始求解。保证尺寸的公差不变仅圆整名义尺寸,并计算尺寸圆整后的目标和约束,以此作为优化结果。选取区间优化结果最优Pareto解集的一部分和确定性最优解列入表2,进行对比分析。

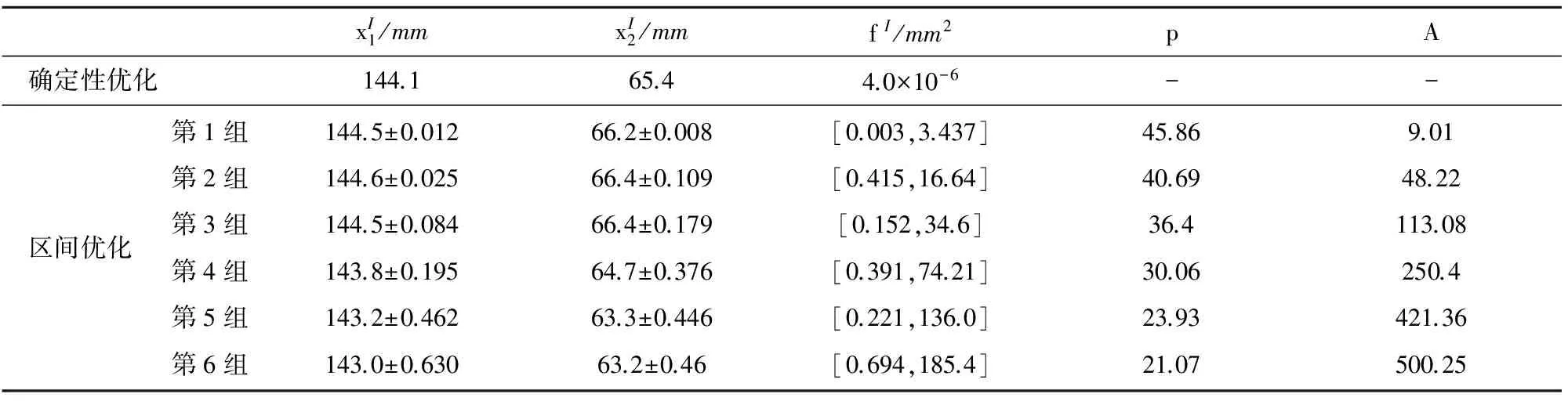
表2 确定性优化结果和区间优化部分结果对比

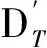
4 结束语

针对因名义尺寸和公差不能同步优化导致火炮制退机结构设计周期长的问题,提出了一种改进的计及公差的区间优化方法。该方法能同步优化火炮制退机关键结构参数的名义尺寸和公差,并在保证制退机原目标性能和约束的同时使得各关键结构尺寸的公差尽量最大化。解析函数对比算例的计算结果表明,采用基于离散化的区间可能度模型能得到目标性能更优的Pareto最优解,改进的公差指标A也更好地反映了平均公差和加工精度的关系。本文工作为研究结构尺寸设计和公差设计的结合提供了一个可供参考的方法,但受限于实验条件,装配误差未加考虑,下一步工作是考虑装配的结构参数优化的实验研究。

[1] 刘启航,徐亚栋,羊柳.节制杆式制退机参数化设计及优化[J].火炮发射与控制学报,2013(4):49-53. LIU Qi-hang,XU Ya-dong,YANG Liu.Parameterization design and optimization of throttling bar recoil mechanism[J].Journal of Gun Launch & Control,2013(4):49-53.(in Chinese)

[2]王冲,邱志平,吴迪,等.结构-声场耦合系统区间鲁棒优化设计[J].振动与冲击,2013,2(17):8-13.

WANG Chong,QIU Zhi-ping,WU Di,et al.Interval robust optimization of a coupled structural-acoustic system[J].Journal of Vibration and Shock,2013,2(17):8-13.(in Chinese)

[3]石海军,钱林方,李淼.具有参数区间不确定的协调器保性能优化[J].兵工学报,2014,35(5):152-157. SHI Hai-jun,QIAN Lin-fang,LI Miao.Guaranteed cost optimization for the shell transfer arm with interval uncertainty[J].Acta Armamentarii,2014,35(5):152-157.(in Chinese)

[4]JIANG C,XIE H C,ZHANG Z G,et al.A new interval optimization method considering tolerance design[J].Engineering Optimization,2015,47(12):1 637-1 650.

[5]袁军堂.机械制造技术基础[M].北京:清华大学出版社,2013.YUAN Jun-tang.Fundamentals of machanical manufacturing technology[M].Beijing:Tsinghua University Press,2013.(in Chinese)

[6]SENGUPTA A,TAPAN K P.On comparing interval numbers[J].European Journal of Operational Research,2000,127:28-43.

[7]姜潮.基于区间的不确定性优化理论与算法[D].长沙:湖南大学,2008. JIANG Chao.Theories and algorithms of uncertain optimization based on interval[D].Changsha:Hunan University,2008.(in Chinese)

[8]王益祥,陈安明,王雅.互换性与测量技术[M].北京:清华大学出版社,2012. WANG Yi-xiang,CHEN An-ming,WANG Ya.Technology of interchange and measurement[M].Beijing:Tsinghua University Press,2012.(in Chinese)

[9]高树滋,陈运生,张月林,等.火炮反后坐装置设计[M].北京:兵器工业出版社,1995:125-127. GAO Shu-zi,CHEN Yun-sheng,ZHANG Yue-lin,et al.Design of recoil system for guns[M].Beijing:Ordnance Industry Press,1995:125-127.(in Chinese)

Research on Optimization for Key Structure Dimension of Gun Recoil Mechanism Considering Tolerance

LI Rong,YANG Guo-lai,LIU Ning,GE Jian-li

(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

In order to explore the long-cycle problem of recoil mechanism’s structure design resulted from that the nominal dimension and tolerance can’t be optimized simultaneously,an improved interval optimization method considering tolerance was proposed to optimize the key structure dimension of the gun recoil-mechanism.The tolerance was assumed to follow normal distribution,and the discretization-based possibility degree model of interval was established,then the tolerance index was improved.The interval optimization model of the key structure parameters of the gun recoil mechanism considering tolerance was developed.Compared with the traditional structural parameters optimization results of gun recoil-mechanism,the key dimensions of the system were optimized,and the design cycle of the gun recoil-mechanism was shortened.The result shows that the Pareto optimum-solution of better objective-performance can be obtained by applying discretization-based interval-possibility-degree model,and the improved tolerance index can reflect the relation of average tolerance and machining precision.

gun;recoil mechanism;possibility degree of interval;coefficient of tolerance grade;dimension optimization

2016-07-21

国防973计划项目(1503613249);国家自然科学基金项目(11172139)

李荣(1991- ),男,硕士研究生,研究方向火炮结构优化与优选。E-mail:lirongwork@qq.com。

杨国来(1968- ),男,教授,博士生导师,研究方向为火炮现代设计理论与方法。E-mail:yyanggl@mail.njust.edu.cn。

TJ303.4

A

1004-499X(2016)04-0080-06