某弹箭转速-攻角闭锁数值仿真及分析

李东阳,常思江,王中原

(南京理工大学 能源与动力工程学院,南京 210094)



某弹箭转速-攻角闭锁数值仿真及分析

李东阳,常思江,王中原

(南京理工大学 能源与动力工程学院,南京 210094)

为了研究转速-攻角闭锁现象的机理和规律,利用滚转角诱导侧向力矩可引起转速-攻角闭锁这一条件,建立了可描述旋转对称弹箭转速-攻角闭锁的动力学模型,并以某弹箭为例进行了数值仿真。研究了初始转速、初始总攻角、初始总攻角方向角以及其他不同参数对转速-攻角闭锁稳态值的影响。仿真结果表明,在相同参数条件下,转速-攻角闭锁状态的稳态值由初始条件决定;当在某参数条件下存在大小相等方向相反的2个稳态转速时,稳态转速会因初始条件的差异而稳定到不同方向,但稳态转速和初始转速方向相同的几率远大于两者相反的几率;在各种参数的共同作用下,为使弹箭运动收敛到稳定的闭锁状态,必须对弹箭气动参数进行合理设计。

弹箭;转速-攻角闭锁;复攻角;非线性气动力矩;数值仿真

转速-攻角闭锁运动可描述为弹箭飞行过程中,转速及总攻角幅值被锁定为常数且总攻角平面与弹体-尾翼固定平面间夹角保持不变的运动[1]。当这一现象发生时,如果被锁定的转速恰好接近弹箭的固有频率,则会引起共振,可导致总攻角增大、飞行失稳;如果被锁定的总攻角为较大数值(如达到20°以上),则容易引起各种复杂的非线性现象,有可能对弹箭的稳定飞行产生不利影响,不但射程大为损失,甚至有可能产生掉弹的严重事故。据公开报道,西班牙Ternel 140 mm火箭弹在28次飞行试验中出现了9次锥形运动,使飞行速度在1.5 s内降低了60%;在我国某些远程火箭飞行试验中,经常发现在弹箭转速设计合理且动态稳定的情况下,仍然会产生飞行不稳,发生近弹和掉弹事故[2]。在某些特殊情况下,该闭锁现象也可加以利用来产生需要的圆锥运动和稳定转速,如针对末敏弹设计稳定转速下的稳态扫描运动[3]。因此,深入研究弹箭的转速-攻角闭锁对实际工程应用具有重要的意义。

目前关于转速-攻角闭锁产生的原因及特点,已有很多学者进行过研究[4-7]。在之前的研究中,转速-攻角闭锁现象的发生总是和弹箭的非对称特性联系在一起,然而Murphy C H[6]指出,对于旋转对称弹箭,若存在随滚转角(定义为总攻角平面与弹体-尾翼固定平面之间的夹角)变化的侧向力矩,转速-攻角闭锁现象也可能发生。为此,Murphy提出了一个转速-攻角闭锁模型,并用一个简单算例进行了验证,但并未给出更多关于不同初始条件、不同参数对转速-攻角闭锁稳态值影响的分析。

针对这一不足,本文在Murphy研究成果的基础上,通过建立转速-攻角闭锁模型,在不同初始条件和不同参数条件下,对该现象进行了数值仿真与深入分析,对其中存在的规律进行了探索。

1 动力学模型

弹箭转速-攻角闭锁动力学模型的建立以弹体坐标系Oxyz为基准,该坐标系与弹体固连,坐标原点在弹箭质心上,x轴沿弹体对称轴方向,指向弹头为正;y轴在弹翼对称平面内与x轴垂直,从弹尾看去指向右为正;z轴方向按右手定则确定。弹箭飞行所受力和力矩按照在该坐标系下的投影进行描述。

弹箭质心速度矢量v、角速度矢量Ω和角动量矢量H在弹体系Oxyz上的分量分别定义为

v=(vxvyvz)

(1)

Ω=(pqr)

(2)

H=(IxpIyqIzr)

(3)

式中:vx,vy,vz和p,q,r分别为弹箭在x,y,z方向上的速度和角速度分量;Ix,Iy,Iz分别为弹体关于x轴、y轴、z轴的转动惯量。

为便于研究,定义复攻角ξ和横向角速度μ为

(4)

(5)

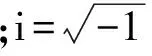
采用如下假设建立复攻角运动模型:

①认为弹体速度、质量和气动力系数在一小段弹道上保持不变;

②小攻角假设,即sinβ+icosβsinα≈β+iα,vx≈v;

③弹体具有对称的质量分布,则各坐标轴为法向惯性轴,并且y轴和z轴的转动惯量相等,不妨记Iy=Iz=It;

④只考虑诱导滚转力矩、诱导侧向力矩和俯仰力矩的非线性,其他力和力矩均为线性。

用无量纲弧长s替代自变量时间t,有:

(6)

根据外弹道理论[8-9],阻力方程为

v′/v=-ACD

(7)

转速方程为

(8)

式中:ρ为空气密度;S为弹箭特征面积;m为弹箭质量;CD为阻力系数;Clp为极阻尼力矩系数导数;Cl0为导转力矩系数;Cln(δ,θ)表示非线性诱导滚转力矩系数,是δ和θ的函数;pss为有差动弹翼时产生的平衡转速;v′表示v对无量纲弧长s的微分。

当pss=0时,方程(8)和文献[6]得到的转速方程相同,虽然ACD量值相对较小,但考虑到对数值积分的影响,当pss≠0时,方程(8)更为合理。

将弹箭质心运动方程和绕心运动方程在Oy、Oz方向上的分量合并,将变量t替换为变量s,化简并略去高阶小量后得复攻角运动方程:

(9)

σ=Ix/It

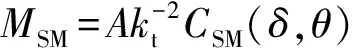
2 数值仿真与分析

2.1 仿真条件

给出简单非线性力矩函数[6]如下所示:

(10)

CSM=a2c0sinkθ

(11)

CM,α=c0(1-c1δ2+a3coskθ)

(12)

式中:k为弹箭尾翼片数;a1,a2,a3为与θ相关的系数,其不等于0时表示各力矩和θ有关;c0,c1为与δ相关的系数。

本文算例为美国一具有4片对称尾翼的大长径比导弹[6],其主要结构参数和气动参数如下所示:

k=4,pss=0,d=0.107 m

v=1 828.8 m/s,m=51.06 kg

Clp=-18,CD=0.4

c0=6.0,c1=25

a1=0.006 9,a2=0.474 7,a3=0

假设各弹道参数和气动参数在短时间内不变,可利用四阶龙格-库塔法对转速方程(8)和复攻角方程(9)进行数值积分。由于仿真用导弹具有4片对称尾翼且各非线性力矩是θ的周期函数,故初始总攻角方向角可在0～90°之间变化,一般ξ′的初值也可设为0。

2.2 不同初始条件下的数值仿真

根据前述动力学模型和仿真条件,选取11种不同的初始条件进行数值仿真,结果如表1所示。表中,δ0,p0,θ0分别为仿真初始总攻角、初始转速和初始总攻角方向角,δ(2),p(2),θ(2)分别为δ(t),p(t),θ(t)在仿真t=2 s时各稳态参数值。由于k=4,根据力矩函数式(10)～式(12),稳态总攻角方向角θ是以90°为周期的函数,则表1中2 s末的总攻角方向角可表示为

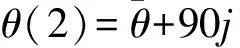
(13)

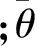
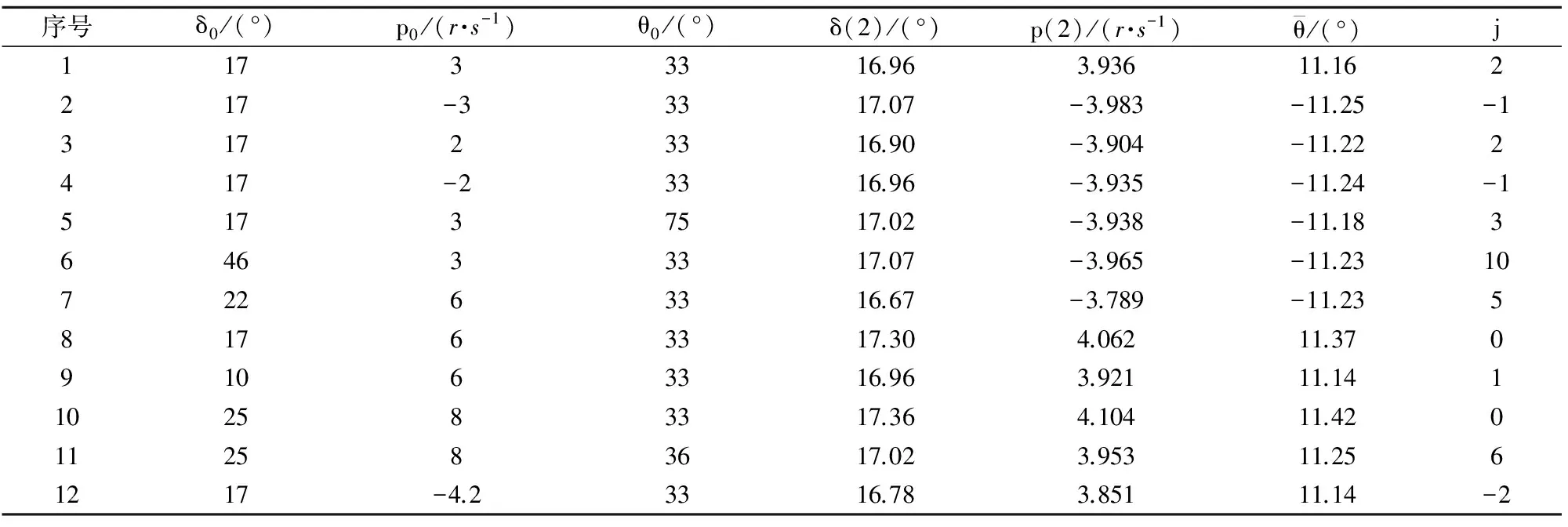
表1 不同初始条件下数值仿真结果

由表中第1、第2和第1、第3种情况可知,初始转速大小或方向不同会使运动收敛到不同稳态(稳态转速方向不同、稳态总攻角方向角不同);从第3、第4种情况可知,初始转速方向不同,最终却收敛到了相同稳态转速,但稳态总攻角方向角不同;从第1、第6和第3、第5种情况可以看出,不同的初始总攻角或总攻角方向角,也会使运动收敛到不同稳态(即不同稳态转速方向、不同稳态总攻角方向角)。由第10、第11种情况可以看出,初始总攻角方向角轻微的变化可能会引起稳态总攻角方向角变化较大。可见,在相同参数条件下,转速-攻角闭锁的具体稳态值由初始条件决定。

从表1还可看出,当初始转速为正时,稳态转速可能为正也可能为负(如第1、第4种情况);同样,当初始转速为负时,稳态转速也可能为正或为负(如第2、第12种情况)。为了研究正负稳态转速出现的概率,引入蒙特卡洛打靶法进行数值仿真实验:δ0服从均匀分布U(0,20)(单位:(°)),θ0服从均匀分布U(0,90)(单位:(°)),当p0服从均匀分布U(0,6)(单位:r/s)时,进行1 000次打靶试验,结果显示稳态转速同样为正的几率约为70%,远大于为负的几率;当p0服从均匀分布U(-6,0)(单位:r/s)时,进行1 000次打靶实验,稳态转速同样为负的几率也约为70%,远大于为正的几率。

表1中第1种条件的闭锁过程如图1所示。

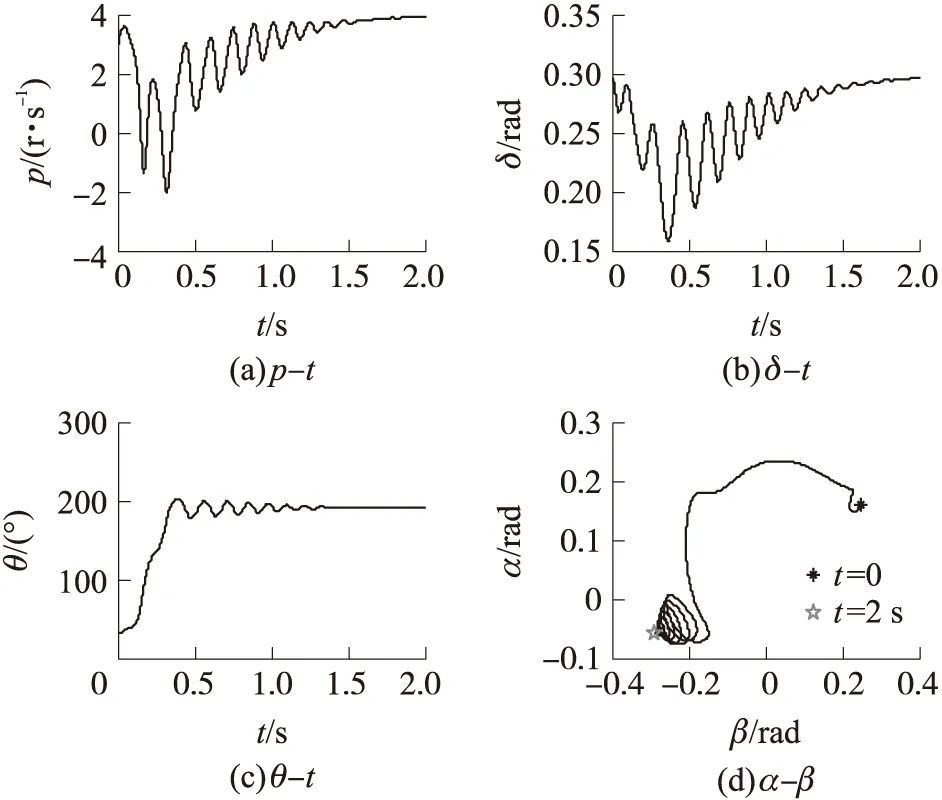
图1 初始条件1对应的转速-攻角闭锁数值仿真曲线

从图1(a)可以看出,在收敛过程中转速的方向改变了4次,最终稳定在和初始转速相同的方向;从图1(c)可以看出,总攻角方向角会由初始值向着稳态值单调增大,最终收敛在稳态值附近;由图1(b)和图1(d)可知,弹箭角运动从第一象限开始沿逆时针变化直至第三象限,总攻角幅值收敛到稳态值(约17°)。

2.3 不同参数条件下的数值仿真

pss表示差动弹翼产生的平衡转速,由力矩函数(12)知,a3表示考虑滚转角对俯仰力矩系数的影响。下面在不同pss和a3参数值且p0=3r/s,δ0=17°,θ0=33°的初始条件下,观察转速-攻角闭锁现象的变化,结果如表2所示。

表2 不同参数条件下数值仿真结果

注:表中“-”表示无稳态值,即不发生转速-攻角闭锁。

表2中第1、第2种情况下,pss=0时,改变a3的值,能发生转速-攻角闭锁。当a3>1.2时,总攻角幅值和方向角先达到稳态值,转速逐渐收敛为0,且a3值越大,转速收敛速度越快。该状态下,弹箭不旋转并以一定的总攻角和总攻角方向角运动。

在第3～第7种参数条件下,a3=0,当pss在0～1.37r/s之间变化时,弹箭运动能在2s内收敛;当pss超过1.37r/s时,运动不收敛,即不产生转速-攻角闭锁,如图2所示。若继续增大pss,转速和总攻角的振荡幅值减小,频率有所增大,平均幅值接近pss。需说明的是,对于不同初始条件,具体临界值也是不同的。

由于差动弹翼可调节弹箭的旋转方向(一般定义右旋为正,左旋为负),故表2中第8和第9条件取pss为负值(即达到平衡转速时弹箭是左旋的)。仿真结果表明,当pss在-1.25～0r/s之间变化时,能发生转速-攻角闭锁,如图3所示(pss=-1.25r/s时的转速-攻角闭锁过程);当pss超过-1.25r/s时将不发生转速-攻角闭锁。

在第10～第12参数条件下,a3=1,pss约在0～1.38r/s之间变化,此时弹箭运动能在2s内收敛,当pss超过1.38r/s时,也不能发生转速-攻角闭锁。

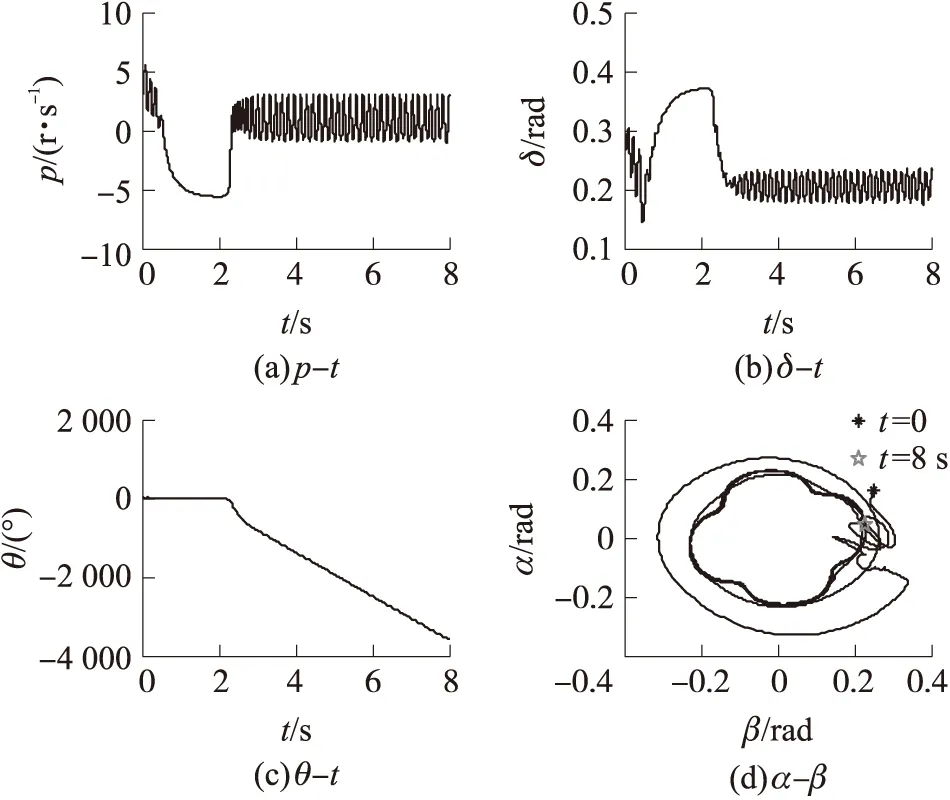
图2 pss=1.38 r/s,a3=0时转速-攻角闭锁数值仿真曲线

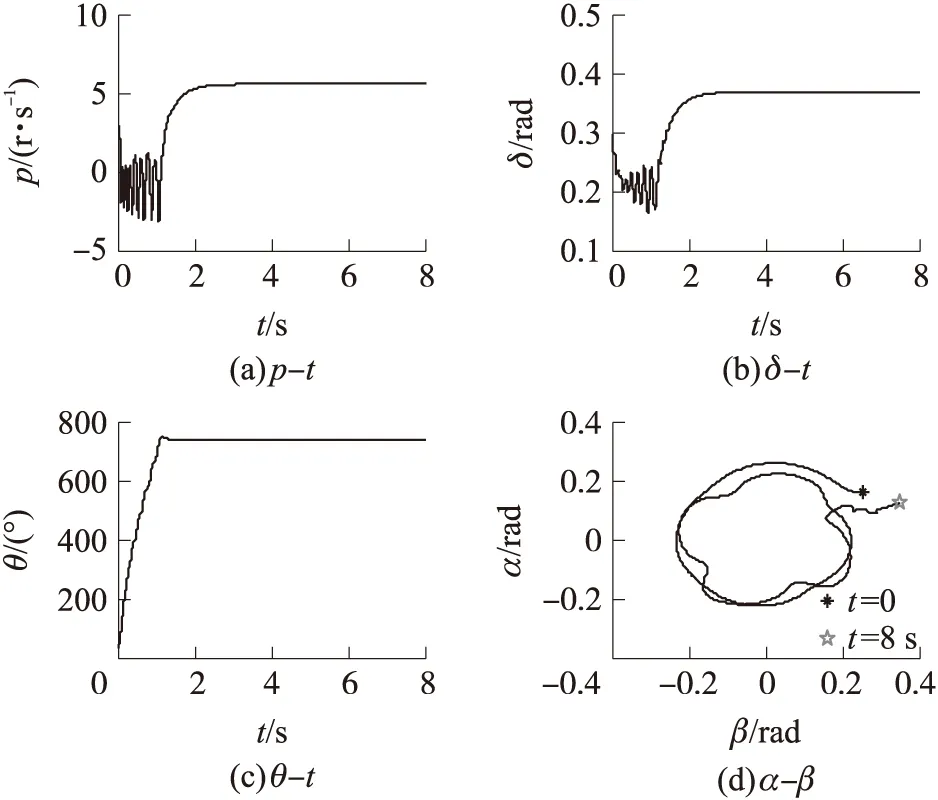
图3 pss=-1.25 r/s,a3=0时转速-攻角闭锁数值仿真曲线

在第13～第14参数条件下,pss=1r/s,a3在0～1.3之间取值时,能发生转速-攻角闭锁现象,a3=1.3时的仿真过程如图4所示,稳态参数振荡幅值较小且在6s末达到稳态。但随着a3的增大,转速和总攻角幅值的振荡幅度加大,收敛时间增大,以致无法达到稳态。

综上可知:当pss=0时,若a3大于某临界值,尽管发生转速-攻角闭锁,但稳态转速为0,稳态攻角及其方向角为非零值;当pss≠0时,若a3大于某临界值,将不发生转速-攻角闭锁。在a3不变的情况下,pss达到或超过一定临界值时,也不发生转速-攻角闭锁。

另外,经数值验证发现,若初始总攻角为0,则不论初始转速和初始总攻角方向角为何值,最终各稳态参数值均为0。

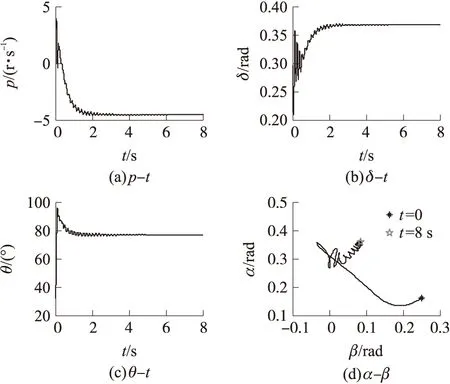
图4 pss=1 r/s,a3=1.3时转速-攻角闭锁数值仿真曲线

3 结束语

本文建立了弹箭转速-攻角闭锁动力学模型,并以某弹箭为例模拟了转速-攻角闭锁的过程,研究了不同初始条件和不同参数对闭锁现象的影响,可得到以下结论:

①在相同参数条件下,闭锁稳态值由初始条件决定;当存在2个大小相等且方向相反的稳态转速时,稳态转速和初始转速方向相同的几率远大于两者方向相反的几率。

②由于平衡转速pss与极阻尼力矩系数导数Clp和导转力矩系数Cl0有关,从理论上讲,如需调节弹箭转速-攻角闭锁的性态,可对Clp,Cl0及a3等气动系数加以合理设计,从而满足一定的弹道要求。

③当初始总攻角为0时,所有稳态参数值均为0。

[1] MURPHY C H.Some special cases of spin-yaw lockin[J].Journal of Guidance and Control,1989,12(6):771-776.

[2]李臣明,刘怡昕.转速闭锁对远程弹箭的影响[J].弹道学报,2010,22(1):45-48. LI Chen-ming,LIU Yi-xin.Effect of roll locking on long-range missile[J].Journal of Ballistics,2010,22(1):45-48.(in Chinese)

[3]MORA N V,PIECHOCKI J,SANZ-ANDRES A.Experimental research on a vertically falling rotating wing decelerator model[C]//19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar.Williamsburg,VA:AIAA,2007:2 007-2 538.

[4]PRICE D A.Sources,mechanisms,and control of roll resonance phenomena for sounding rockets[J].Journal of Spacecraft and Rockets,1967,4(11):1 516-1 523.

[5]CLARE T A.On resonance instability for finned configurations having non-linear aerodynamic properties[J].Journal of Spacecraft and Rockets,1971,8(3):278-283.

[6]MURPHY C H,MEIMAGEN W H.Spin-yaw lock-in of a rotational symmetric missile[J].Journal of Guidance,Control,and Dynamics,2009,32(2):377-382.

[7]舒敬荣,张继春,常思江.空气动力非对称弹丸大攻角旋转共振运动研究及应用[J].兵工学报,2014,35(4):421-427. SHU Jing-rong,ZHANG Ji-chun,CHANG Si-jiang.Research on large angle-of-attack spin resonance movement[J].Acta Armamentarii,2014,35(4):421-427.(in Chinese)

[8]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2014. HAN Zi-peng.Exterior ballistics of projectiles and rockets[M].Beijing:Benjing Institute of Technology Press,2014.(in Chinese)

[9]李奉昌,韩子鹏.弹丸非线性运动理论[M].北京:机械委兵工教材编审室,1988.

Numerical Simulation and Analysis for Spin-Yaw Lock-In of a Missile

LI Dong-yang,CHANG Si-jiang,WANG Zhong-yuan

(School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

In order to study the mechanism and law of spin-yaw lock-in,the equations of motion for a rotationally symmetric missile were derived based on the fact that spin-yaw lock-in can occur with a side moment varying with the roll angle between the angle of attack plane and a fixed plane.Taking a missile for an example,the effects of different parameters and initial conditions,including initial spin rate,initial angle of attack and initial roll angle on the stable equilibrium state of lock-in motion were analyzed.Simulation results show that the stable state is a function of initial conditions under the same parameter condition.When there are two stable spin rates with the same magnitude and opposite directions,the occurrence of positive and negative spin is up to initial conditions while the stable spin rate is more likely to have the same direction with initial spin rate.It is necessary to design a reasonable value for specific parameters to make the lock-in motion occur.

missile;spin-yaw lock-in;complex angle of attack;nonlinear aerodynamic moment;numerical simulation

2016-07-01

国家自然科学基金项目(11402117);中国博士后科学基金项目(2013M541676)

李东阳(1992- ),女,博士研究生,研究方向为外弹道理论及应用。E-mail:lidongy0502@gmail.com。

常思江(1983- ),男,讲师,博士,研究方向为外弹道设计理论、弹箭飞行控制技术。E-mail:ballistics@126.com。

TJ760.1

A

1004-499X(2016)04-0012-05