16MnR钢埋弧焊工艺参数优化及焊缝尺寸预测

张立斌，姚玉环，邓　宇，王海泉

（广东石油化工学院，广东茂名525000）

16MnR钢埋弧焊工艺参数优化及焊缝尺寸预测

张立斌，姚玉环，邓宇，王海泉

（广东石油化工学院，广东茂名525000）

为准确获得16MnR钢埋弧自动焊工艺参数及其焊缝几何尺寸，利用正交回归设计方法和二次回归组合设计方法分别对焊接工艺参数与板厚δ、焊接工艺参数与焊缝几何尺寸的关系进行了优化试验；并利用“spss”软件对试验结果进行了统计分析与检验，建立了焊接电流I、焊接电压U、焊接速度v与板厚δ以及焊缝几何尺寸RB和RE与焊接工艺参数间的数学模型。

正交回归设计；工艺参数；优化：二次回归正交组合设计；焊缝尺寸

0　前言

埋弧自动焊焊接16MnR钢不仅具有生产效率高、焊接质量好等优点，而且还具有节能省材及降低劳动强度的特点，一直是常用的高效自动化焊接方法。在该焊接工艺过程中，首先要解决的问题就是确定正确的焊接工艺参数。因为焊接工艺参数直接影响焊缝金属的合金化、冶金性能和力学性能以及焊缝的几何形状尺寸等[1-3]。快速、准确地获得焊接工艺参数并有效预测焊缝的几何尺寸，一直是焊接工程技术人员需要解决的重要问题。

利用单元正交多项式回归设计和二次回归正交组合设计方法，对16MnR钢埋弧自动焊单面焊双面成形工艺参数与焊接工件厚度、焊缝正面的溶宽和加强高等几何尺寸与焊接工艺参数的关系进行了优化试验研究，寻求建立焊接工艺参数与工件厚度δ以及焊缝几何尺寸与工艺参数的数学模型[4-5]。

1　16MnR钢焊接工艺参数与板厚关系的优化

1.1试验材料、设备及方法

本试验所用材料为16MnR，焊丝选用φ4.0 mm的H08MnA，配431焊剂；试件尺寸500 mm×200 mm，厚度δ=4～14 mm，不开坡口，留有间隙c；接头形式如图1所示，平焊；电源选用MZ1-1000 DC埋弧焊机，直流反接，在试件两端加装引弧板和收弧板。焊前烘干焊剂，对焊丝和钢板进行除油污和去锈处理，衬垫采用方槽铜垫板+焊剂，强迫冷却成形方式。

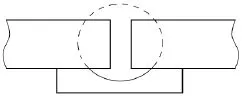
图1　单面对接焊（焊剂—铜垫）

1.216MnR钢焊接工艺参数优化分析

虽然对16MnR钢埋弧焊质量的影响较为复杂，但当焊件已知时，对焊接质量的影响主要表现在焊接电流I、焊接电压U和焊接速度v，因上述三个工艺参数主要由工件厚度δ决定，在此取板厚δ为因素，其水平间隔Δ=1 mm，则因素δ的水平数N为

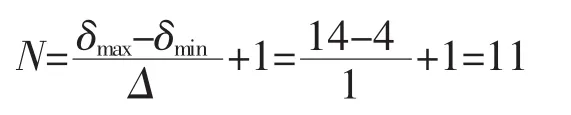
试验方案如表1所示。正交多项式组φi（δ）（i= 0，1，2，…）的具体形式见式（1）。其优化准则为：第一，焊缝无缺陷，且形状尺寸合理；第二，焊丝及焊剂的消耗量最少；第三，焊接效率最高；第四，焊接能量消耗最少。在上述条件下，对应的焊接工艺参数为最佳。从而得到焊接工艺参数I、U及v与工件厚度δ的数学关系[5]。

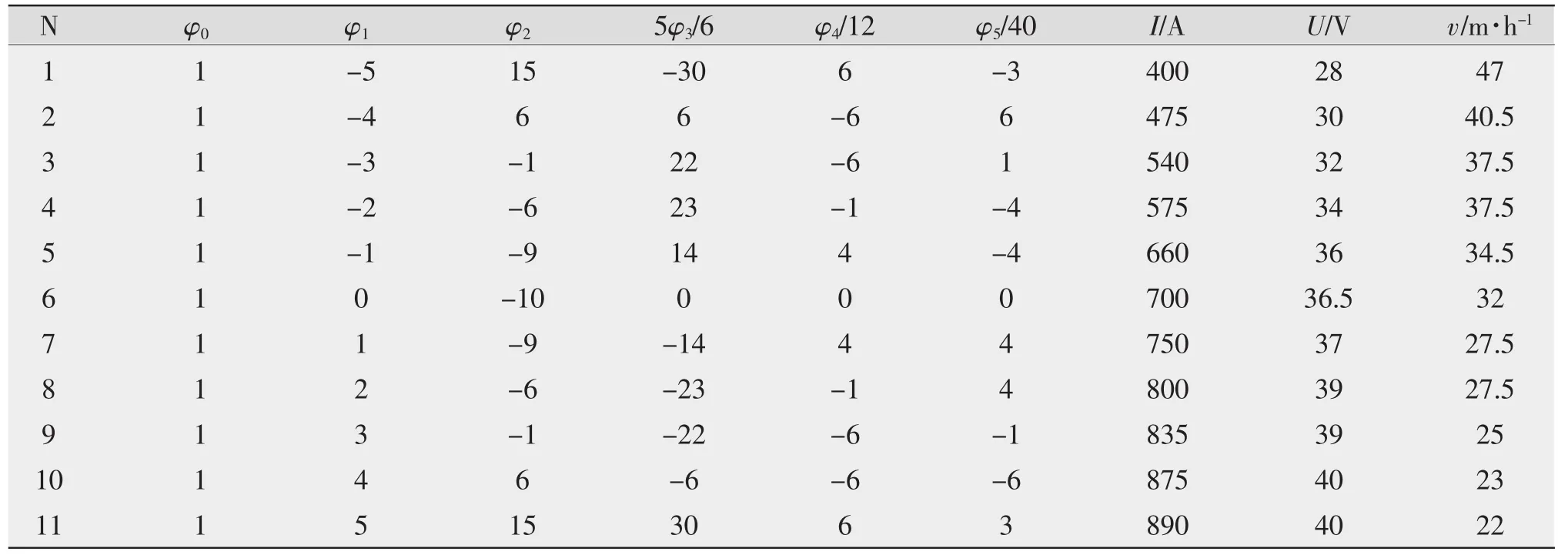
表1　试验方案

1.316MnR钢焊接工艺参数的回归模型

1.3.1回归模型的选取

为全面研究16MnR钢厚度δ对焊接工艺参数的影响，选取的回归模型见式（2），它在编码空间的形式见式（3）[6]

1.3.2模型系数的回归

利用“spss”软件对模型系数进行统计分析，结果如表2所示。由表2可知，当显著水平α=0.01时，模型的回归系数bn0、bn1、bn2均显著，而其他回归系数不显著，从方程中剔除，故得回归方程见式（4）。

1.3.3回归模型检验及结果分析

由“spss”软件分析得到回归模型的检验结果见表3所示。回归方程式（4）的F值分别为510.453、173.164和112.335，表明方程的显著性较高；方程的拟合优度R2分别为0.998、0.994和0.991，调整后的拟合优度R2分别为0.996、0.989和0.982，说明回归方程拟合非常好。将编码式（1）代入回归模型式（4），整理得到16MnR钢埋弧焊焊接工艺参数与厚度δ的回归数学模型，见式（5）。

表2　焊接工艺参数回归结果

表3　回归模型的检验结果

2　焊缝几何尺寸预测

由式（5）确定的焊接工艺参数，对厚度分别为4 mm、6 mm、8 mm、10 mm、12 mm、14 mm的试件进行单面埋弧焊双面成形试验，在保证正、反面成形质量的情况下，确定了一组正反面成形良好的焊接工艺参数，如表4所示；据此，利用二次回归正交组合试验设计技术确定埋弧自动焊单面焊双面成形焊缝几何尺寸与焊接工艺参数之间的关系，考核的指标有两个：即焊缝正面熔宽RB和余高RE；虽然焊缝背面熔宽BB和余高BE也随着焊接工艺参数发生变化，但BB与BE主要受到工件间隙c及衬垫规格尺寸的限制而变化范围有限，所以本试验主要研究焊缝正面熔宽RB和余高RE的变化规律。为了考核交互作用对试验指标的影响，选择了工程上常用的二次完全代数式作为数学模型：试验选择三个因素，其变化范围如表5所示。

表4　不同板厚的焊接工艺参数

表5　自然因素水平及其编码公式表

按预定的方案进行试验，焊后截取焊缝的横截面、磨光、腐蚀后测量焊缝几何形状尺寸RB、RE的平均值，具体试验方案及结果如表6所示。

2.1回归模型的选择

为研究16MnR钢埋弧焊焊接工艺参数及其交互作用对焊缝几何形状尺寸的影响规律，选择的回归模型见式（6），它在编码空间的形式见式（7）

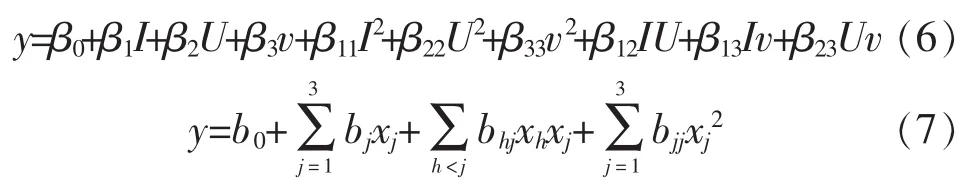
2.2模型系数的计算与统计检验

按表6的方案进行试验，统计分析焊缝正面熔宽RB、余高RE的回归模型，结果如表7所示。由表7可知，当显著水平α=0.01时，模型的回归系数b0、b1、b2、b3、b11均显著，而其他回归系数不显著，从方程中剔除，故得回归方程如式（8）所示。

2.3回归方程检验与分析

由“spss”软件分析得到回归方程的检验结果如表8所示，回归方程（8）的F值分别为124.179和133.458，表明方程的显著性较高；方程的拟合优度R2分别为0.993和0.993，调整后的拟合优度R2分别为0.985和0.986，说明回归方程拟合的非常好。将表5的编码公式代入回归方程（8）并整理得16MnR钢埋弧焊焊缝正面熔宽RB及余高RE与焊接工艺参数的模型见式（9）[6]

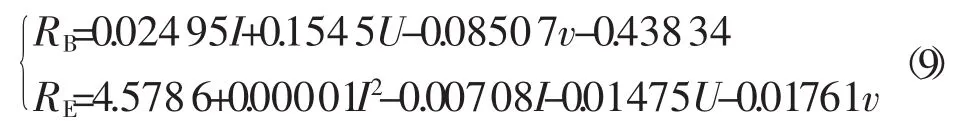
由式（9）可知，焊缝正面熔宽RB随焊接电流与焊接电压的增加而增大，随焊接速度的提高而减小；焊缝余高RE随着焊接电压及焊接速度的增大而减小，随着焊接电流的增大表现出先减后增的变化趋势，当焊接电流等于354 A时，余高RE为最小值。而354 A又小于本试验的最小电流值（本试验最小电流值为470 A），故在本试验范围内，可认为随着焊接电流的增加而焊接余高RE亦增大。焊缝正面熔宽RB与余高RE的试验优化值与理论计算值如表9所示。RB与RE的试验优化值和理论计算值间的最大偏差分别为ΔRB=0.51 mm，ΔRE=0.12 mm。

表6　埋弧自动焊单面焊双面成型焊缝尺寸试验方案及其结果

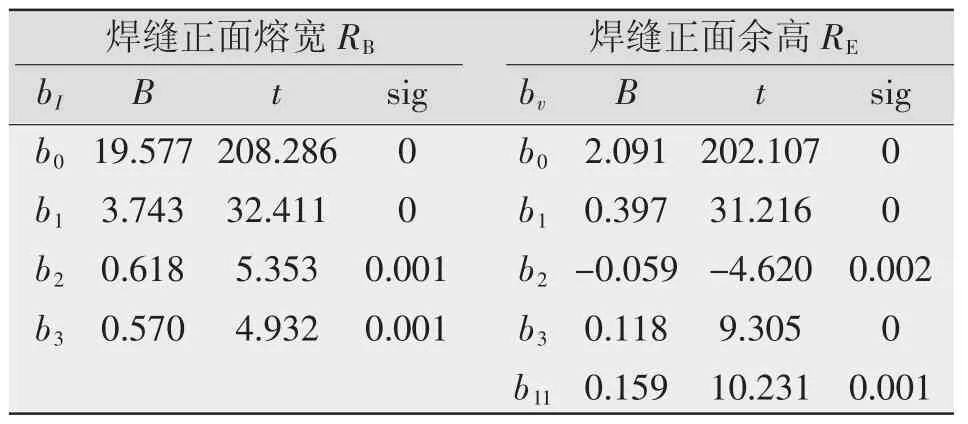
表7　焊缝几何尺寸回归结果

表8　回归方程的检验结果

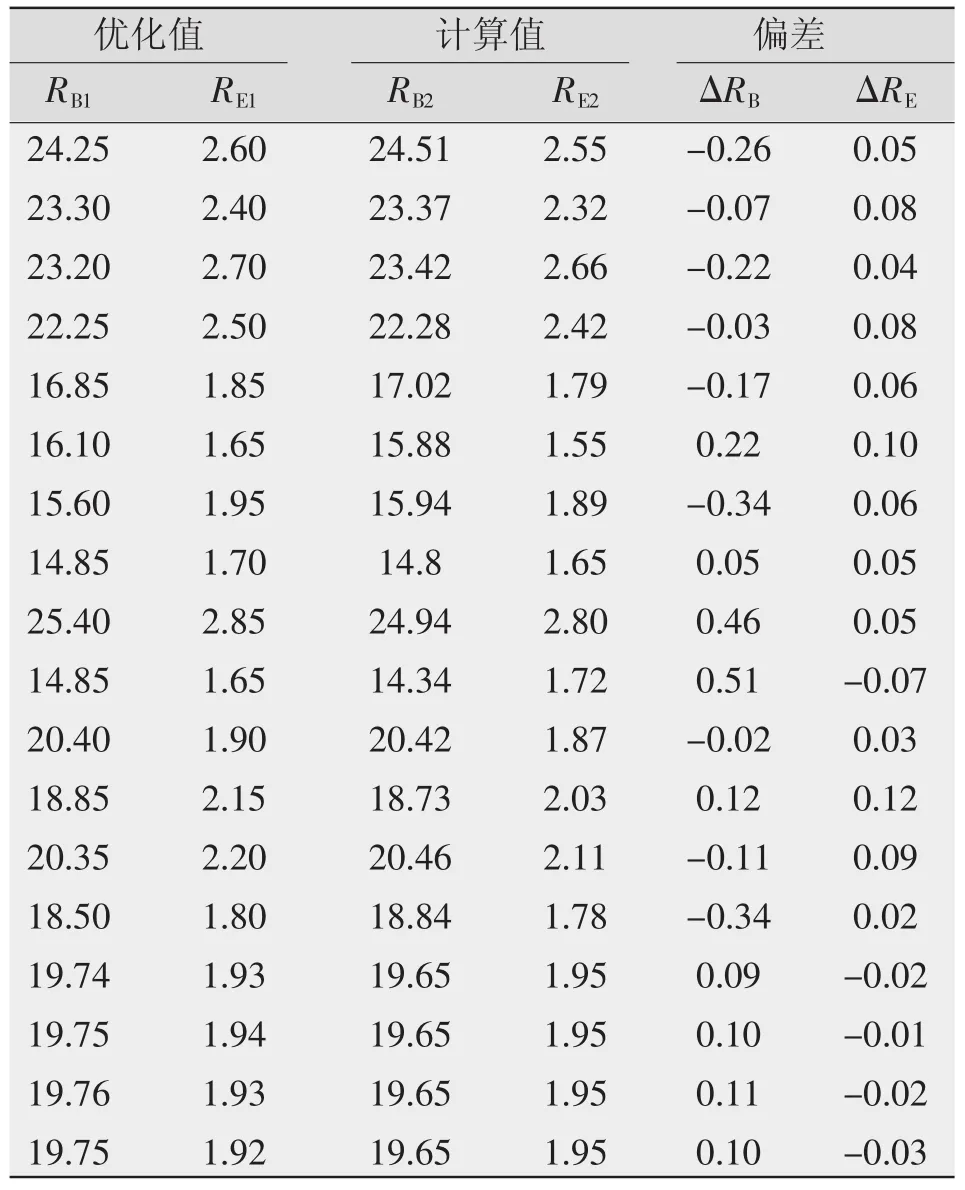
表9　RB与RE的优化值与计算值对照表mm

3　结论

利用单元正交多项式回归设计方法对16MnR钢中、薄板埋弧焊单面焊双面成型焊接工艺参数与工件厚度δ的关系进行了优化试验，建立了焊接工艺参数与δ的数学模型；还利用二次回归正交组合设计方法对焊缝正面几何尺寸RB、RE与焊接工艺参数的关系进行了优化试验研究，建立了两者间的数学模型。

利用所建立的数学模型，既可以确定16MnR钢中、薄板埋弧焊单面焊双面成形的焊接工艺参数，还可以预测焊缝正面几何尺寸，对指导实际生产及建立中、薄板埋弧焊计算机控制系统具有参考作用。

[1]叶建雄.焊接工艺参数优化的智能计算研究[J].材料导报，2009，23（12）：69.

[2]张海兵.焊缝性能影响因素的研究进展[J].材料导报，2011，25（10）：114.

[3]王海波.多层多道埋弧焊工艺参数优化设计方法[J].电焊机，2012，42（8）：6-10.

[4]张立斌.埋弧焊工艺参数优化与模型建立[J].焊接技术，2014，43（1）：22-24.

[5]王海波，张建优等.多层多道埋弧焊工艺参数优化设计方法[J].电焊机，2012，42（8）：11-15.

[6]任露泉.回归设计及其优化[M].北京：科学出版社，2000.

Process parameters optimization and the weld dimension prediction of 16MnR steel for submerged arc automatic welding

ZHANG Libin，YAO Yuhuan，DENG Yu，WANG Haiquan
（Guangdong University of Petrochemical Technology，Maoming 525000，China）

In order to obtain the process parameters and the weld dimensions of 16MnR steel for submerged arc automatic welding accurately，the optimizing experiment was made for the relationship of welding process parameters and the thickness by using orthogonal regression design method.At the same time，the optimizing experiment was made for the relationship of welding process parameters and weld geometry sizes by using the quadratic regression combination design method.Statistical analysis and inspection of the test resultswere made by"spss"software，the mathematical model which of the welding current，the welding voltage，the welding speed and thickness was been establish，as well as the mathematical model which of the weld geometry size and the weld process parameters was established.

orthogonal regression design；process parameters；optimization；quadratic regression orthogonal combination design；weld size

TG457.11

A

1001－2303（2016）03－0152-05

10.7512/j.issn.1001-2303.2016.03.32

2015－02－06；

2015－03－20

张立斌（1963—），男，黑龙江五常人，教授，主要从事焊接及特种材料应用的研究工作。