低温下船用钢材弹塑性曲线研究

任 祎 刘娴如 李建光

（西南林业大学，云南 昆明 650000）

0 引言

近年来，随着经济全球化的持续发展，工业的发展带动了国际船市的繁荣，随着海洋中各种矿产资源的开发，船舶的应用领域进一步扩大［1］。由于船舶在航行过程中要承受风浪的冲击和交变负荷的影响，尤其是船舶在低温地区航行时，会面临着恶劣的低温环境。低温时，大多数金属钢材的力学性能会受到影响，会出现由韧变脆的现象，所以船体结构用钢的要求非常严格。

本研究采用EH36船用钢来制作试件，并参考金属低温下的试验方法，对试件进行三种低温下的单向拉伸试验，分析试验数据后得出本构关系。本构关系的建立不仅是塑性力学的基础，也是塑性力学的主要研究内容之一［2］。采用弹性-幂次强化模型本构关系进行拟合，假设混合强化模型，将有效塑性应变作为强化参数，得出在某一预加应变时逆向加载的一维应力-应变关系，对低温环境下船用钢材弹塑性曲线的研究至关重要。

1 本构关系的建立

金属材料发生变形时，应力随应变变化的规律为金属材料的本构关系，本构关系是研究材料变形的基础［3］。为了能完整的表达出弹塑性反应，运用加载准则、流动法则、强化法则强化参数和相容条件等概念进行描述，其是塑性理论框架的基础［4］。在某一塑性变形状态下，给物体施加一荷载增量，设该荷载增量产生的应力增量和应变增量分别为dσ和dε，应变增量dε可分解为弹性应变增量dεe和塑性应变增量dεp［5］，见式（1）。

应力增量与应变增量的表达式见式（2）。

式中：ε为应变；Et为切线模量，其表达式见式（3）。

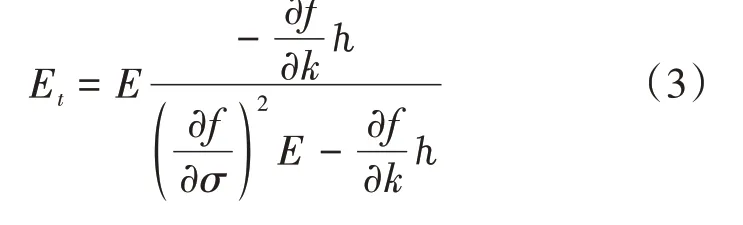
式中：E为杨氏模量；f为屈服函数；k为强化函数标量；σ为应力；h为标量函数。其增量表达式见式（4）。

对于有效塑性应变εp，其计算公式见式（5）。

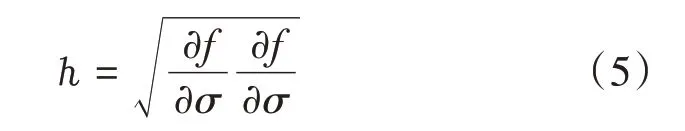
对于塑性功WP，其计算公式见式（6）。

本研究根据材料特性，假设运用混合强化法则，其加载函数见式（7）。

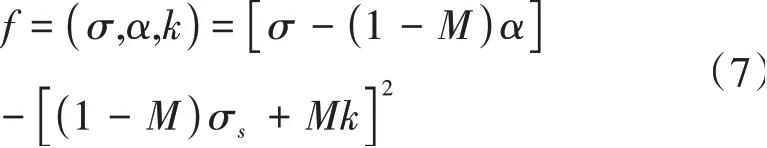
式中：α为反应力；k为强化函数；σs为初始屈服应力；M为混合强化参数，从0到1变化。反应力α也是塑性加载历史的函数，其增量形式见式（8）。

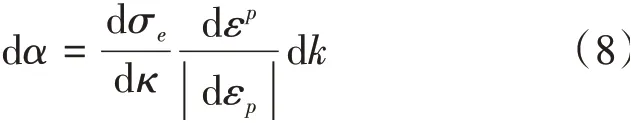
式中：σe为有效应力，反应加载阶段应力改变的方式；εp为有效塑性应变。

2 试验及数据拟合

2.1 试验方案

本研究进行低温状态下EH36钢的准静态拉伸试验，应变率控制在2×10-4s-1，总共设置3个温度点，即-10℃、-20℃和-40℃，并对每个温度点进行两组试验，试验结果取平均值。根据试验可得出EH36钢在3个不同低温下的屈服强度σs，并得到EH36钢低温状态下的应力-应变关系曲线。

本研究选用的试件是EH36钢，采购于无锡，母材钢板的尺寸为500 mm×400 mm×20 mm。根据《金属材料低温拉伸试验方法》（GB/T 228—2010）标准的要求，将母材钢板切割加工成试验所需的三个试件，试样直径为40 mm，平行段长度分别为120 mm、60 mm和60 mm。其中，长试件用于进行-40℃试验。通过加入液氮，对带温度箱的MTS试验机进行降温处理。先将试件固定在温度箱中，分别将温度降到-10℃、-20℃和-40℃，等试件在温度箱中固定1 h后再进行低温状态下的拉伸试验，试验设备如图1所示。

图1 拉伸机

2.2 试验数据及分析

对EH36钢在低温状态下进行拉伸试验，得到三种不同低温状态EH36钢的应力-应变关系曲线，如图2所示。

图2 应力-应变关系曲线

根据试验数据，得到-10℃、-20℃和-40℃时，EH36钢的相关力学性能，如表1所示。

表1 不同温度下EH36钢的力学性能

本研究利用弹性-幂次强化模型来描述EH36钢的强化特性，其表达式见式（9）。

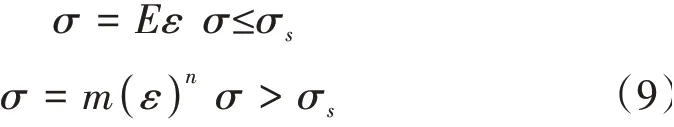
式中：σs为材料屈服点对应的应力值；m和n均为材料参数。

通过非线性拟合，得出材料参数，从总应变中减去弹性应变，转化成应力与塑性应变的关系，如图3所示。

图3 不同温度下应力与塑性应变关系图

强化阶段，在-10℃、-20℃和-40℃时拟合出来的应力与塑性应变的表达式见式（10）。

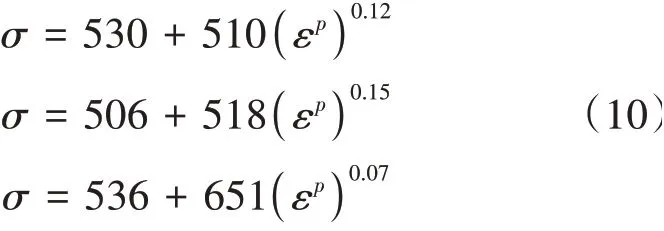
3 有效塑性应变标定弹塑性曲线

塑性变形历史用强化参数这一标量的当前值来表示，本研究所用的塑性强化参数为有效塑性应变εp。

根据EH36钢的材料特性，假设遵循混合强化法则，即0＜M＜1。在-10℃、-20℃和-40℃时分别运用两种强化参数来标定EH36钢的弹塑性曲线。预加应变至εp=0.002，求得此时逆向加载的一维应力-应变关系。

当温度为-10℃时 ，将有效塑性应变εp作为强化参数，由有效塑性应变的定义可得εp=εp，见式（11）。

当0＜εp≤0.002时，弹塑性应力-应变关系见式（12）。

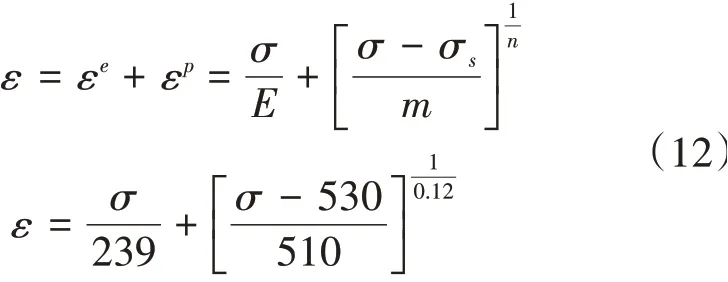
可得到对应预加应变εp=0.002的应力和应变。σ=771.93 MPa，ε=0.005 229 8。

由公式（8）得出反应力α的值，即α=241.93 MPa、k=771.93 MPa。

根据混合强化法则，取M=0.3，其反映了该点的屈服函数，见式（13）。

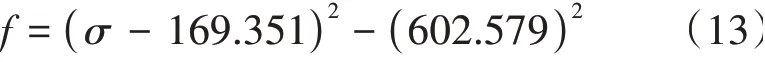
此式反应f在逆向加载阶段直到σ达到-433.288 MPa时，只有弹性应变产生变化，此时的总应变为ε=0.001 865。

由式（3）、式（5）、式（7）、式（8）和式（11）的切线模量Et的表达式，见式（14）。

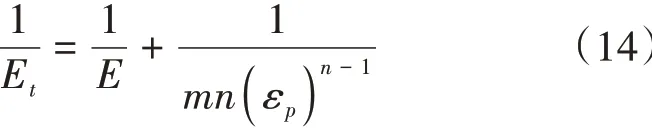
超过σ=-433.228 MPa，材料发出压缩弹塑性变形，在这个阶段，保持dεp=-dεp，所以有εp=0.004-εp。

由式（2）得式（15）。

最终导出后继加载阶段的应力-应变关系，见式（16）。

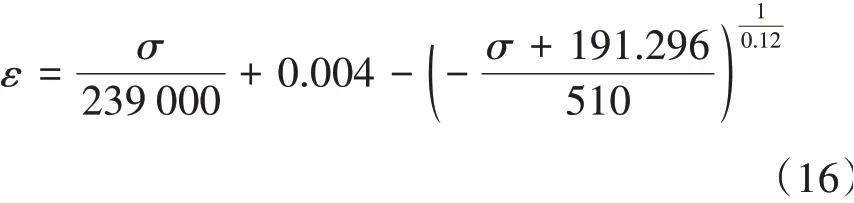
当0＜εp≤0.002时，弹塑性应力-应变关系见式（17）。

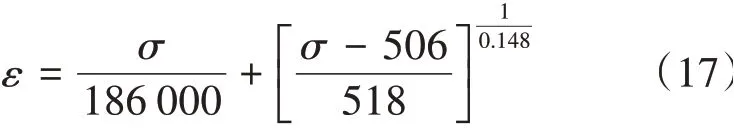
同理可得，当对应于预加应变εp=0.002时，σ=712.48 MPa、ε=0.005 83、α=206.482 MPa、k=712.48 MPa。

根据混合强化法则，取M=0.1，屈服函数见式（18）。

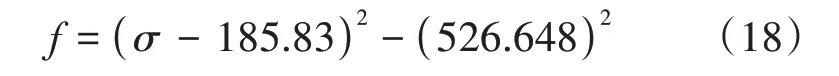
其反应f在逆向加载阶段直到σ达到-340.82 MPa时，只有弹性应变产生变化，此时的在总应变为ε=0.000 167。

此时，求得切线模量Et的表达式为所以，后继加载阶段的应力-应变关系可由同样的处理方法，见式（19）。

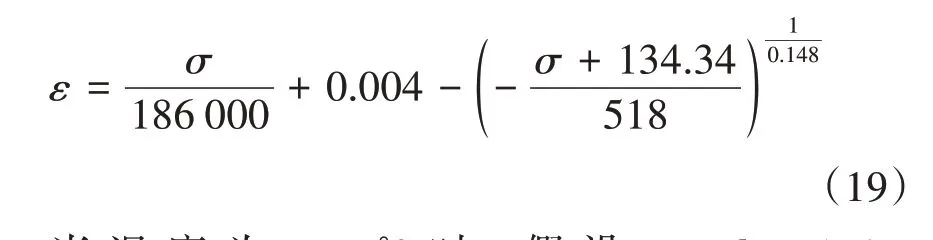
当0＜εp≤0.002时，弹塑性应力-应变关系见式（20）。

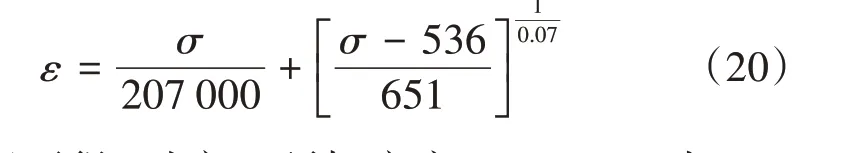
同理可得，对应于预加应变εp=0.002时，σ=957.36 MPa、ε=0.006 625、α=421.36MPa、k=957.36 MPa。

根据混合强化法则，取M=0.3，屈服函数见式（21）。

其反应f在逆向加载阶段直到σ达到-367.456 MPa时，只有弹性应变产生变化，此时的在总应变为ε=0.000 224 9。

后继加载阶段的应力-应变关系可由同样的处理方法得到，见式（22）。

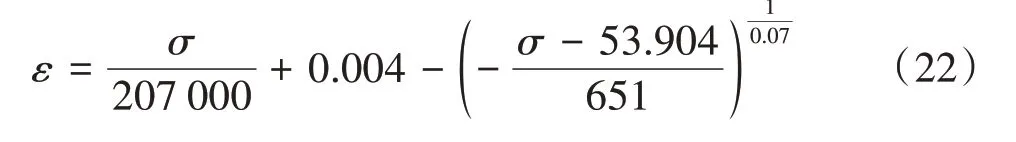
4 结语

本研究选用EH36船用钢，通过三种低温状态（-10℃、-20℃和-40℃）下的单向拉伸试验获得EH36钢的应力-应变关系曲线。塑性强化参数采用有效塑性应变εp，计算得出预加应变时逆向加载的一维应力-应变关系，为此类材料力学特性的研究提供参考。