中国老龄人口死亡率建模及预测

郑 静，张桂军，黄佩佩

(杭州电子科技大学数学研究所，浙江 杭州 310018)



中国老龄人口死亡率建模及预测

郑 静，张桂军，黄佩佩

(杭州电子科技大学数学研究所，浙江 杭州 310018)

我国老龄人口死亡率在时间上存在高度线性相关性，并且其对数死亡率的改善速度存在非线性特征.根据我国老龄人口实际死亡率特点，提出一个新的模型，使得这些性质在模型中得到体现.并针对我国老龄人口死亡率数据较少的特点，使用MCMC方法对模型参数进行估计，预测时充分利用参数的分布信息，给出未来几年死亡率的均值和分布情况，从而使预测结果更加可信.

老龄人口死亡率；马尔科夫链蒙特卡罗方法；Lee-Cater模型

0 引 言

全球人口死亡率经历了一百多年的持续下降，而且这种趋势仍在持续，但引起死亡率下降的原因发生了一些变化.文献[1]提出，早期的死亡率下降主要是由新生儿的成活率提高引起，近年来主要来源于70岁以上人口的增多.因此，对老龄人口死亡率的建模和预测显得尤为重要.

早期应用最广的老龄人口死亡率模型是Gompertz模型，这个模型是单因子的死亡率模型，对高龄人口估计值偏大.文献[2]中的经典Lee-Cater模型也存在同样问题，对老龄人口死亡率预测不够准确.2005年，文献[3]提出了Logistic模型，它刻画的是单因素年龄的死亡率；正如Lee-Cater模型并不适用于英国和澳大利亚，Logistic模型对我国的老龄人口死亡率数据拟合的准确度也不够.近年来，文献[4-5]利用Lee-Cater的确定模型和随机化模型对中国的死亡率进行建模，文献[6]研究了我国老年人口的死亡率趋势.本文在经典Lee-Cater模型的基础上，提出了一种新的老龄人口死亡率模型，根据1994—2012年我国老龄人口死亡率数据，用MCMC算法对模型进行了验证，并对未来10年的死亡率进行了预测.

1 模型构造

1.1 经典Lee-Cater模型

经典Lee-Cater模型最初用于美国人口死亡率的建模，其原始模型为：

ln mx,t=αx+βxkt+εx,t

(1)

其中：mx,t为x岁人群在t年的中心死亡率；αx为特定x岁人群的平均对数死亡率；kt为对数死亡率随时间t的变化程度，也称为死亡率指数；βx为特定x岁人群对数死亡率对kt的依赖程度；εx,t为残差项，假设服从均值为0，方差为σ2的正态分布.为了得到唯一的解，还需将参数进行标准化：∑βx=1,∑kt=0.在Lee-Carter模型中，kt有一个负的漂移项，从而对数死亡率表现为线性下降趋势.Lee-Carter模型的主要缺点是所有年龄死亡率的下降速度都由同一kt决定，从而导致了老年人口死亡率预测值偏高.

1.2 我国老龄人口死亡率数据分析

本文的分析数据来源于中国统计年鉴(1994—2012)[7]、中国人口与就业统计年鉴(1994—2012)[8]，经过数据分析，得出我国老龄人口死亡率有以下特征.

1)老龄人口死亡率与时间高度相关.

2013年，文献[9]指出，老龄人口死亡率与时间高度相关的.为了考察我国老龄人口死亡率的相关性，本文引入时间效应项，用来消除各年龄组死亡率因在时间上的共同驱动而存在的相关性.定义移除年效应的老年人口死亡率的相关系数为：

(2)

移除年效应的老年人口死亡率的相关性不再具有一致性，相关系数的绝对值小于0.6，说明56～90岁的死亡率的高度线性相关性主要表现在年时间效应上.

2)我国老龄人口对数死亡率呈非线性变化.

在相关分析中，死亡率在时间项存在时为高度一致的线性相关，移除后表现出弱相关性.在经典的Lee-Cater模型中，时间项βxkt为带负漂移的随机游走，这意味着时间项的线性下降，从而对数死亡率线性下降.我国老龄人口对数死亡率改善速度不是线性变化的，存在速度的改变.将死亡率时间趋势项进行分解，在模型中考虑对数死亡率下降速度的变化.

令ωx,t=ln mx,t-αx-κt，ωx,t的一阶差分为Δx,t=ωx,t+1-ωx,t，

根据1994—2012年我国人口死亡率数据分析老龄人口死亡率的改善速度趋势项，得到的结果如表1所示.

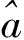
表1 a的估计值和估计方差

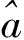
1.3 双重时间效应的Lee-Cater模型

由前面的分析，针对我国老龄人口的死亡率的特点，本文提出以下模型：

(3)

其中，mx,t为年龄x岁在第t年的死亡率；参数αx为x岁年龄组的人口历年平均对数死亡率，度量x岁人口死亡率的平均水平；κt为第t年对各年龄组死亡率影响；参数λ为死亡率长期改善因子，反应死亡率在随时间改变的同时，各年龄组自身死亡率的改善程度；βx为改善因子，反映不同年龄组死亡率改善的速度，βx为正值时表示该年龄组的死亡率改善速度低于死亡率改善的平均水平，为负值时表示死亡率改善速度高于平均水平.

2 模型拟合

经典的Lee-Cater模型采用奇异值分解来估计参数然后进行二次估计，是利用假设死亡人口服从Poisson分布对参数进行极大似然估计，这些估计方法都难以给出参数的分布信息.MCMC方法不需要做额外的假设，也不需要二次估计，同时能给出估计量的区间估计.在进行预测时，MCMC方法考虑了估计参数的分布信息，从而能保证在数据量较少的情况下，模型估计参数对数据的依赖，保证模型的稳定性.

2.1 MCMC参数估计方法

数据来源为中国人口与就业统计年鉴和人口普查.从相关性分析中知道，55岁的死亡率和其它年龄组的死亡率有较大差异，在模型计算中选取1994—2012年的56～90岁的人口死亡率数据拟合模型：

ln mx,t=αx+κt+βxe-λt+εx,t

(4)

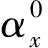
2.2 参数的估计值及其分布

在实验中，共计迭代1 500次.去掉前面500个迭代值，利用样本均值作为估计量的估计值，样本的第50个次序统计量和第950个次序统计量构成估计量的95%置信区间，各参数的估计值如图1—4所示.

图1 αx的估计

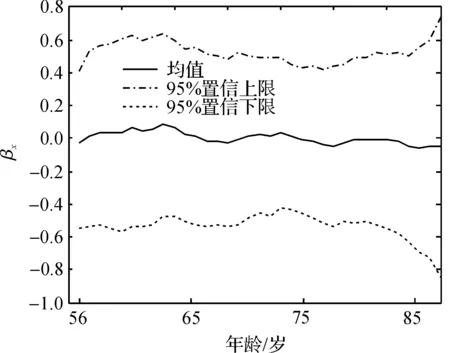
图2 βx的估计

图3 κt的估计

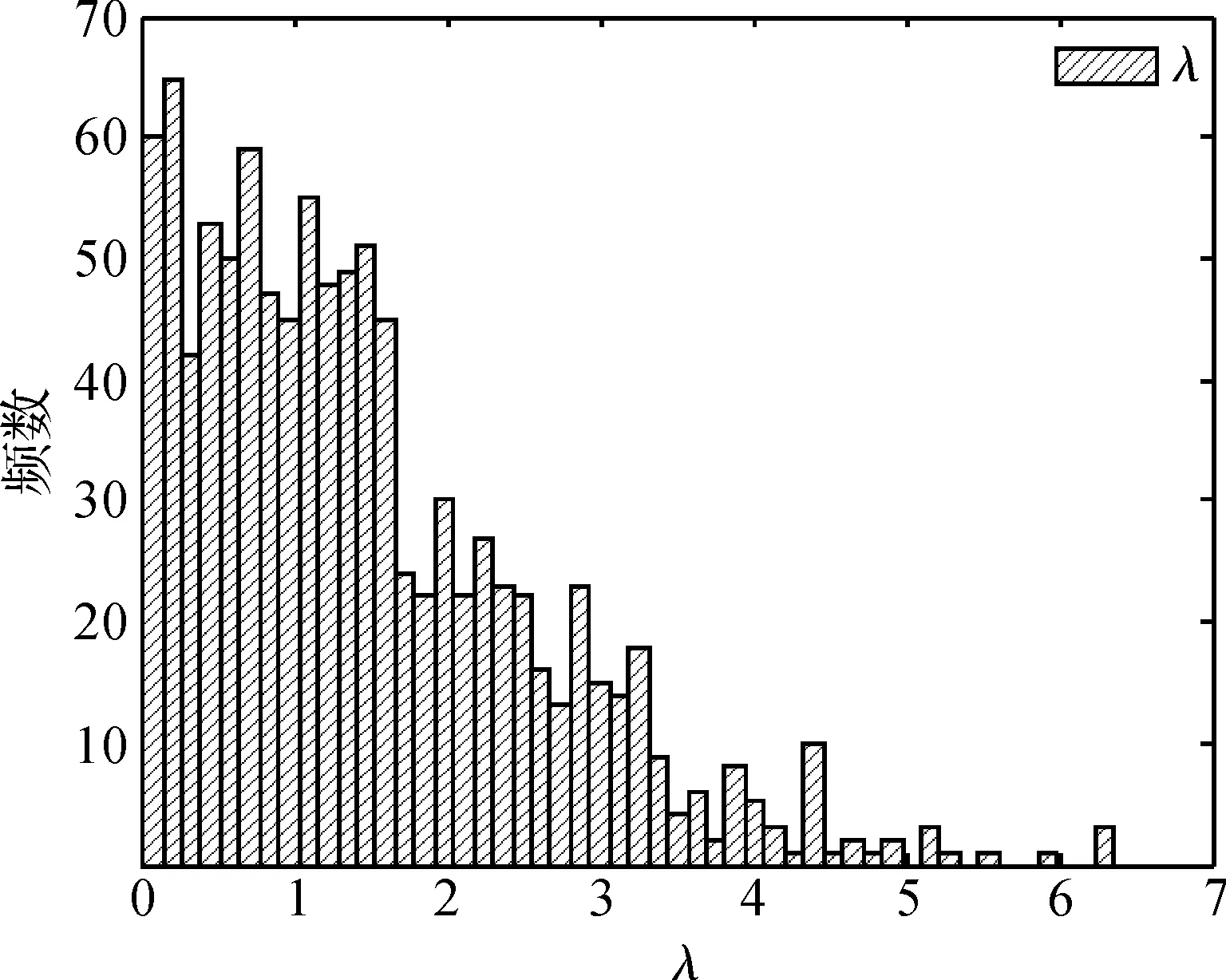
图4 λ的样本直方图

图1—3中点划线为估计参数的95%置信上限，虚线为估计参数的95%置信下限.图1是死亡率中心水平αx的估计值，死亡率中心和年龄之间近似的线性关系.图2中改善速度βx在56～77岁更趋向取正值，而之后的死亡率趋向取负值，在77岁之前的死亡率中，死亡率改善速度小于整体趋势，77岁之后的改善速度比整体水平更快，从而还有更大的改善空间.图3为的短期趋势κt估计值，可以看出，在整体上κt有线性下降的趋势.图4为长期趋势项λ的直方图，大于0的λ表示死亡率具有非线性下降趋势.

2.3 拟合误差

根据1994—2012年的56～90岁的人口死亡率数据，并利用MCMC算法进行参数估计，拟合绝对误差如图5所示，模型拟合的残差相关性如图6所示.

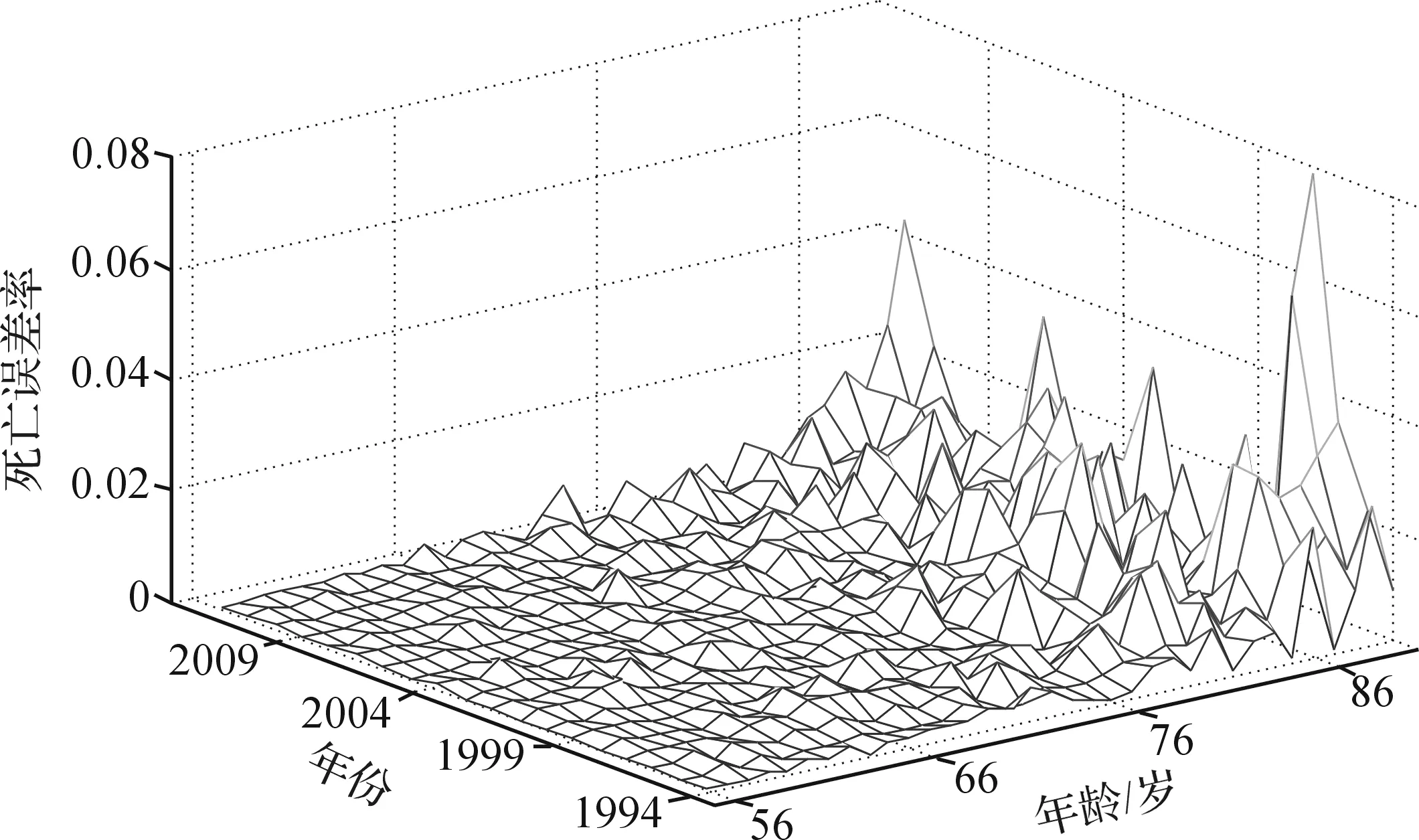
图5 绝对误差

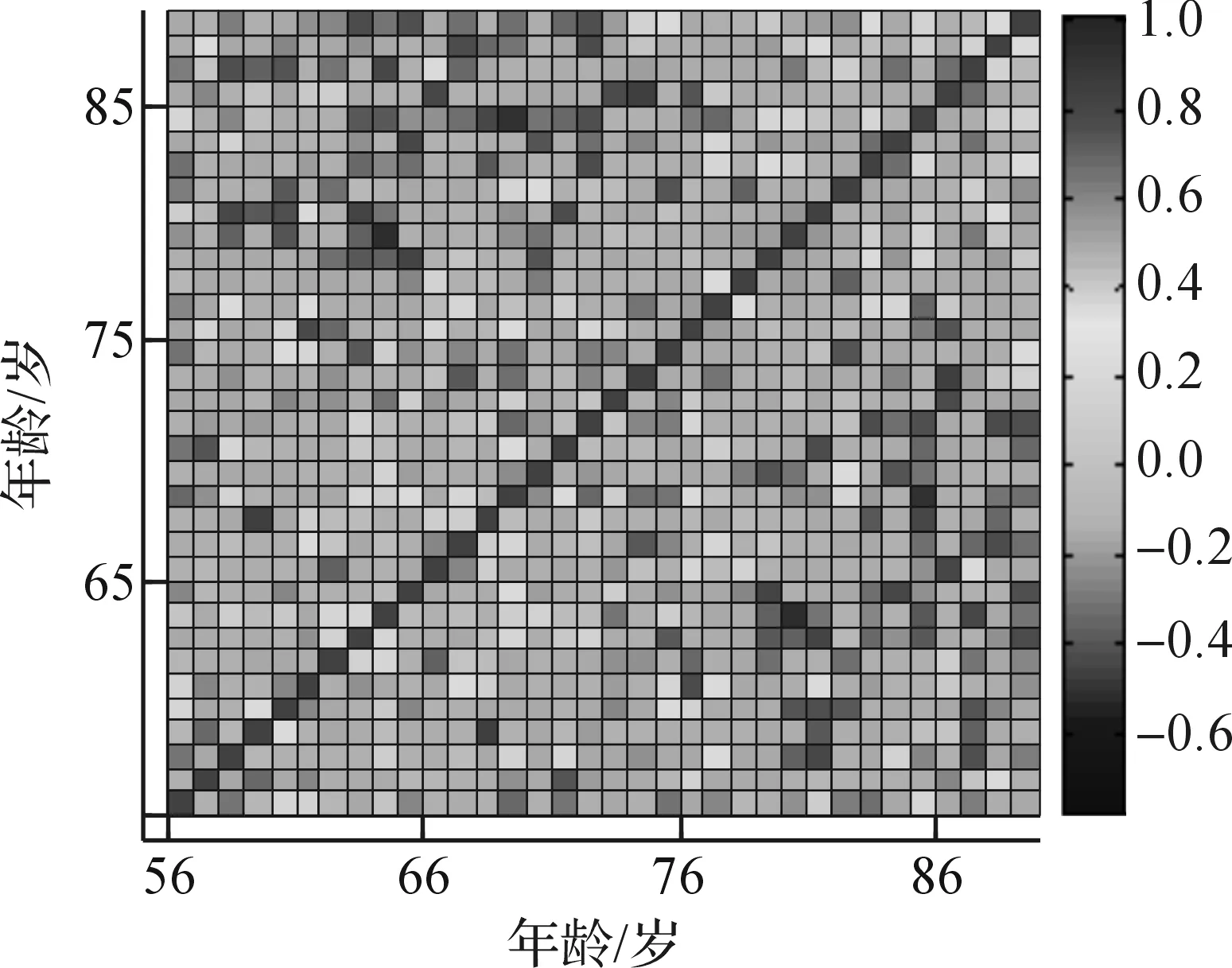
图6 残差相关性

从图5可以看出，模型的误差都非常小，特别是在85岁以下，绝对误差为0.02，然而在85岁以上，误差增加，这主要是因为这5个年龄组人口基数小，并且本身数据波动大.图6已经没有显著的相关性，说明本文所用的模型是充分的.

部分年龄死亡率的误差的相关统计如表2所示.

表2 死亡率拟合误差

从表2可以看出，绝对误差最大的88岁组的相对误差为3.01%，绝对误差下的相对误差为10.21%，其它组均在10%以下.

3 老龄人口死亡率预测

3.1 死亡率模型检验

接下来研究模型的预测表现，需要对短期时间趋势项κt进行外推，从图3中可以看出，κt有近似下降趋势，序列均值存在漂移，利用时间序列方法对κt项进行建模，拟合模型为：

(5)

κt是含有一个单位根的非平稳过程，并且有一个负的漂移，κt的一阶差分为AR(1)模型.模型中常数项的方差为0.000 3，一阶滞后系数的方差为0.032 0.模型的常数项为-0.03，从而死亡率在总体上有-0.02的改进速度.为了验证模型的预测表现和稳定性，分别以1994—2011年、1994—2010年、1994—2009年为原始数据对2012年死亡率进行一步，二步、三步预测，图7为模型依赖不同数据下对2012年预测，图8为利用2011年之前数据对2012年进行预测的90%置信区间.

图7 预测2012年死亡率

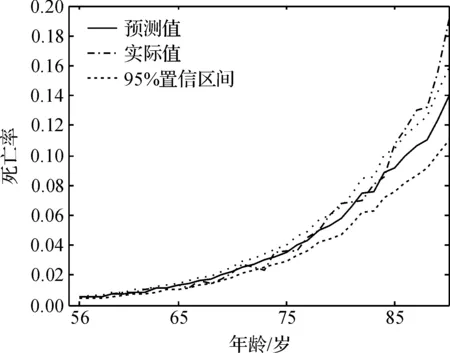
图8 预测2012年死亡率置信区间

对比图7中3个估计值的曲线，不同数据预测的2012年死亡率之间偏差很小，即使在高年龄组，不同预测值之间偏差也很小.在多步预测和实际值之间，56～64岁的估计和实际值基本重叠，65～75岁之间死亡率估计偏低，76～85岁的死亡率估计值和实际值相互交错.从图8中可以看出，所有死亡率的估计在90%的置信区间以内.86岁及其以上年龄组死亡率被低估，其实际值在90%的置信区间以外，这个年龄段实际死亡率高于模型估计的死亡率.

由图7和图8可以看出，模型在预测时对原始数据依赖较小，模型比较稳定.在90%的置信区间以内，85岁以下预测都是在预测区间内部，特别是在低年龄组，死亡率的预测在均值上，结合表2的数据，在低年龄组的死亡率拟合相对误差为6%，模型在稳定性和精确性上都有良好表现.

3.2 未来10年死亡率预测

图7显示说明，模型没有出现过拟合现象，并且在多步预测上预测均值和实际死亡率也相差很小，可知模型在多步预测上有较高的精度.利用时间序列对κt进行预测，从而预测未来10年的死亡率，如图9、10所示.

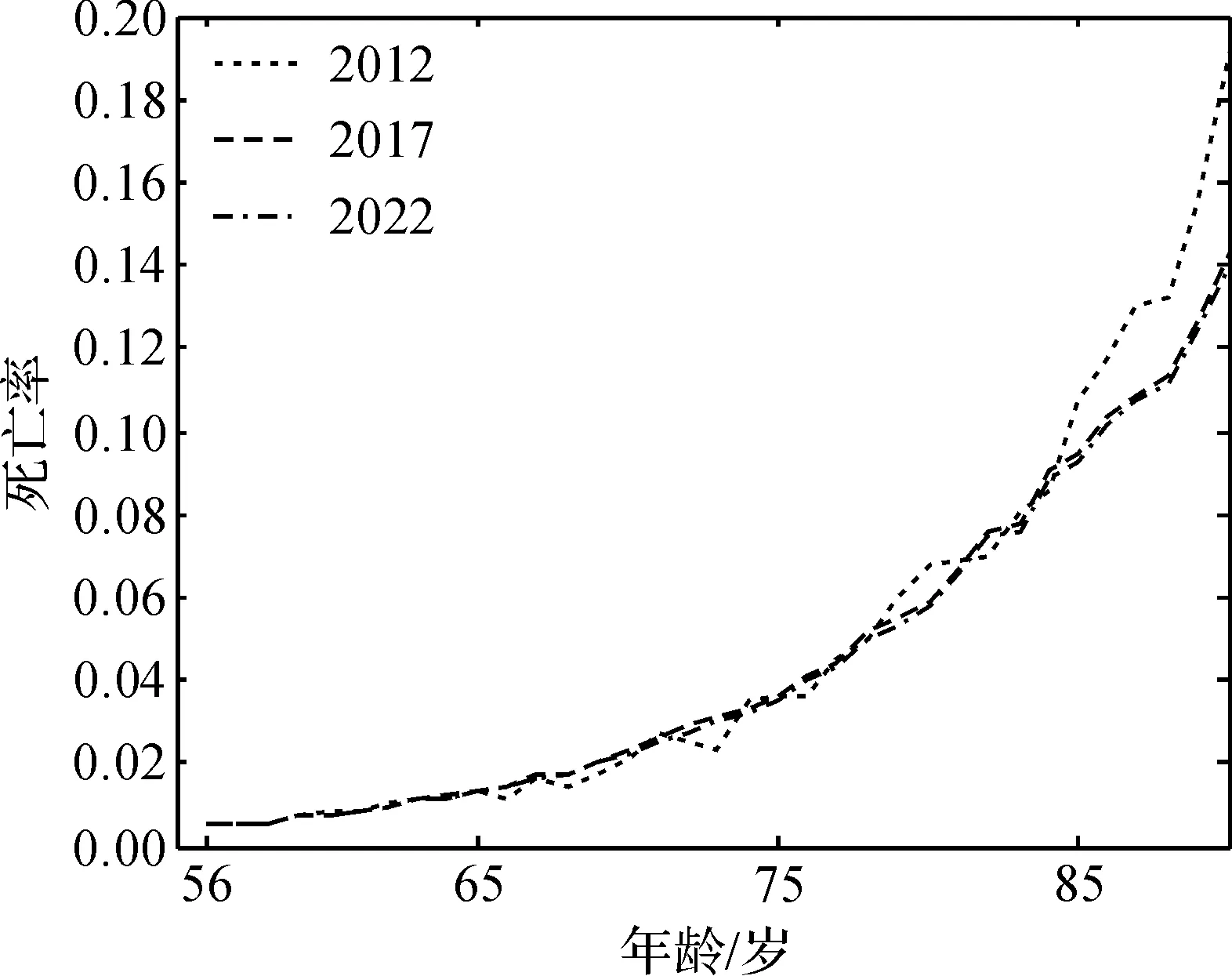
图9 2017年和2022年预测死亡率

图10 2022年预测死亡率置信区间

从图9中可以看出，2017年和2022年死亡率的差异非常小，说明未来10年老年人口死亡率呈下降趋势.从置信区间中也可以看出预测死亡率在分布上是有偏的.可以得出以下几点结论：1)2012—1017年的死亡率改善效果不明显，而在2017—2022年的死亡率改善明显.2)年龄较高的死亡率改善要比年龄较小的死亡率改善更快.未来10年内，74岁以下的死亡率基本没有改善的迹象，然而85岁以上死亡率改善明显.3)到2022年，在95%的置信区间内，死亡率水平不会超过2012年的死亡率水平，同时，未来死亡率的改善区间非常大.

4 结束语

本文重点研究了我国老龄人口的死亡率建模及预测问题，在经典的Lee-Cater模型的基础上，提出一个全新的模型，双重时间效应的Lee-Carter模型.把死亡率随时间的改善分解为短期改善和长期改善，其中在短期改善上，利用随机游走建模，在长期改善上，利用指数函数建模，并利用MCMC方法进行参数估计和预测.本文的模型在预测时考虑了参数的分布，很好地克服了因我国老龄人口的死亡数据不足造成的参数波动问题，从而在不同的历史数据下都有较好的预测表现.

[1]WILMOTH J R, DEEGAN L J, LUNDSTRÖM H, et al. Increase of maximum life-span in Sweden, 1861-1999[J]. Science, 2000, 289(5488): 2366-2368.

[2]LEE R D, CARTER L R. Modeling and forecasting US mortality [J]. Journal of the American statistical association, 1992, 87(419): 659-671.

[3]BONGAARTS J. Long-range trends in adult mortality: Models and projection methods[J]. Demography, 2005, 42(1): 23-49.

[4]王晓军,任文东.有限数据下Lee-Carter模型在人口死亡率预测中的应用[J].统计研究,2012,29(6):87-94.

[5]吴晓坤,王晓军.中国人口死亡率Lee-Carter模型的再抽样估计、预测与应用[J].中国人口科学,2014(4):27-34.

[6]王晓军,赵明.中国高龄人口死亡率随机波动趋势分析[J].统计研究,2014,31(9):51-57.

[7]中华人民共和国国家统计局.中国统计年鉴[DB/OL].[2015-12-01].http://tongji.cnki.net/kns55/Navi/HomePage.aspx?id=N2010100096&name=YINFN&floor=1.

[8]国家统计局人口和就业统计司.中国人口和就业统计年鉴[DB/OL].[2015-12-01].http://tongji.cnki.net/kns55/navi/YearBook.aspx?id=N2014050071&floor=1.

[9]MITCHELL D, BROCKETT P, MENDOZA-ARRIAGA R, et al. Modeling and forecasting mortality rates[J]. Insurance Mathematics & Economics, 2013, 52(2): 275-285.

Modeling and Forecasting for Chinese Aging Population Mortality

ZHENG Jing, ZHANG Guijun, HUANG Peipei

(InstituteofMathematics,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

There is a high linear correlation for Chinese aging population mortality about time. It exits nonlinear characteristics to the rate of improvement of logarithm mortality. In this paper, we propose a new model to fit the characteristics of the actual mortality rate of aging population. MCMC method is used to estimate the parameters of the model, which can solve the problem of less data of aging population. Using MCMC methods, the mean and distribution of forecasting mortality are given. The prediction results are more credible because our method utilizes distribution information about the parameters.

aging mortality; MCMC method; Lee-Cater model

10.13954/j.cnki.hdu.2016.06.015

2016-03-31

郑静(1970-)，女，安徽安庆人，副教授，统计学.

C812

A

1001-9146(2016)06-0071-06