严格半正张量特征值互补问题的Pareto-谱估计

凌莉芸，凌 晨

(杭州电子科技大学理学院，浙江 杭州 310018)



严格半正张量特征值互补问题的Pareto-谱估计

凌莉芸，凌 晨

(杭州电子科技大学理学院，浙江 杭州 310018)

针对一类严格半正张量特征值互补问题，研究了其Pareto-特征值的符号特征.在此基础上，利用严格半正张量的常量定义和算子定义，得到了严格半正张量特征值互补问题的Pareto-特征值的上下界估计.

张量；严格半正张量；Pareto-特征值；Pareto-谱

0 引 言

张量特征值互补问题[1]是矩阵特征值互补问题[2-3]和张量特征值问题[4-5]的自然推广，它与矩阵特征值互补问题类似，在许多工程领域有广泛应用[1].但与矩阵特征值互补和张量特征值问题比较,张量特征值互补问题的计算更难[6].例如，求最大Pareto-特征值是NP-难问题，因此需要进行相关估计.本文研究了严格半正张量特征值互补问题的Pareto-谱估计.结合算子范数的性质，刻画严格半正张量特征值互补问题的Pareto-特征值的符号特征和上下界估计，对进一步研究结构性张量特征值互补问题具有重要的理论意义.

1 问题描述及相关预备知识

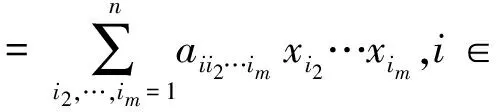
本文考虑张量特征值互补问题,即求λ∈R和x∈Rn{0},使得：

(1)

下面首先给出有关定义和引理.

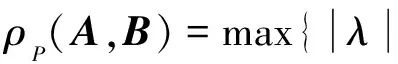
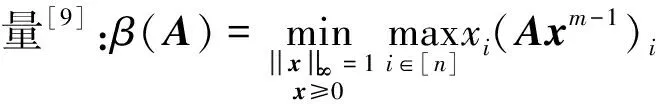
引理1[9]设A∈Tm,n.则A是严格半正张量，当且仅当β(A)>0.

命题1 设A∈Tm,n.若A为严格协正，则A必为严格半正.

下面的例子表明，严格半正张量未必是严格协正张量.

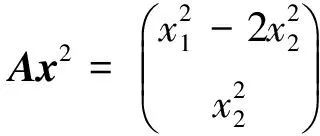
针对给定的A∈Tm,n，现在定义连续正齐次算子TA∶Rn→Rn如下：

特别地，若m是偶数，还可定义另一连续正齐次算子FA∶Rn→Rn：

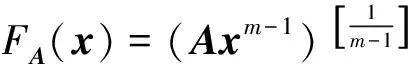
(2)

引理2[10]设A∈Tm,n,则有：

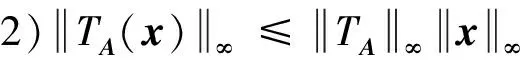
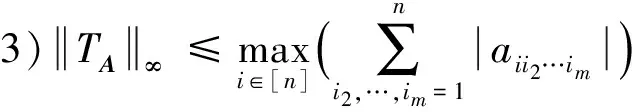
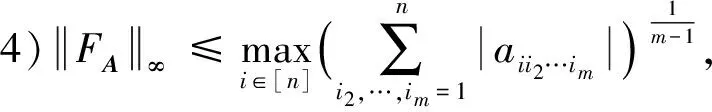
引理3[10]设A∈Tm,n,且A≥0(即A中任一元均非负)，则有：

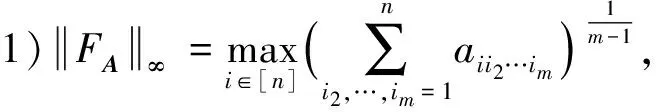
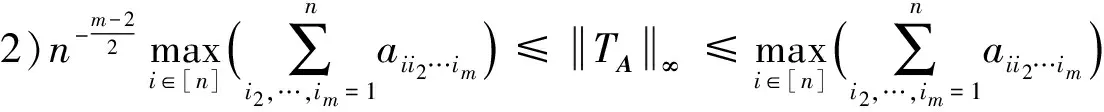
2 主要结果

在文献[1]中所需条件更弱的假设下，考虑式(1)的Pareto-谱估计.首先，讨论A为严格半正且B=-I情形时A的Pareto-特征值符号.

命题2 设A,B∈Tm,n.若A为严格半正且B=-I，则(A,-I)的任一Pareto-特征值均是正的.

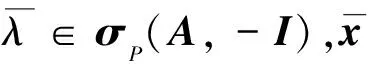
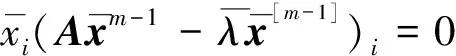
(3)

下面的定理进一步刻画A的Pareto-谱的上下界.

定理1 设A,B∈Tm,n.若A为严格半正且B=-I，则：

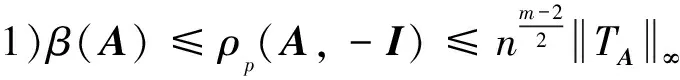
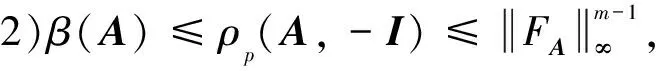
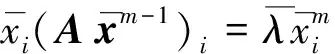
(4)

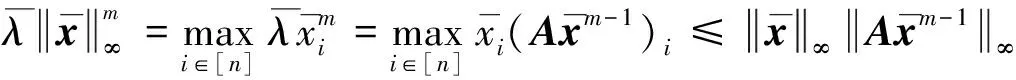
(5)

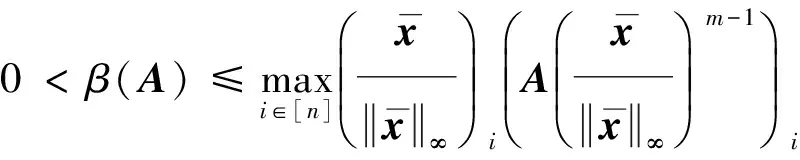
(6)

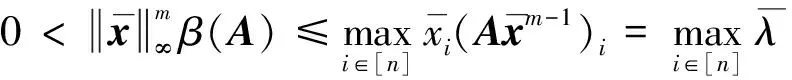
由引理2和定理1，得到下面的结论.

推论1 设A,B∈Tm,n.若A为严格半正，且B=-I，则：

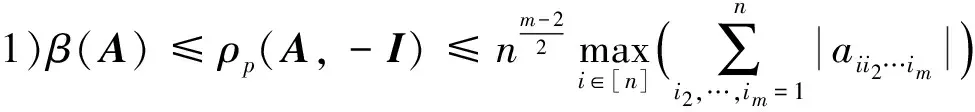
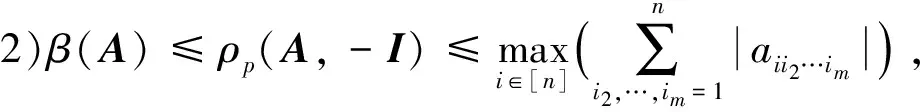
下面讨论A为严格半正且B≥0情形时(A,B)的Pareto-特征值符号和上下界.

命题3 设A,B∈Tm,n.若A为严格半正且B≥0，则(A,B)的任一Pareto-特征值均是负的.

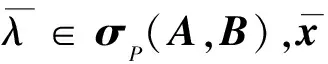
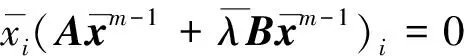
(7)

下面的定理进一步刻画(A,B)的Pareto-特征值的上下界.

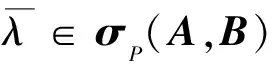
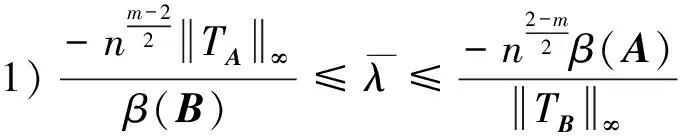
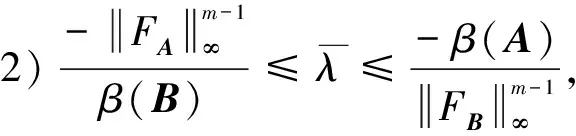
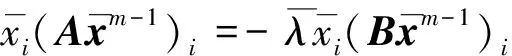
(8)

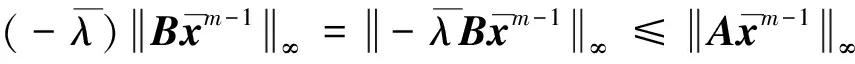
(9)

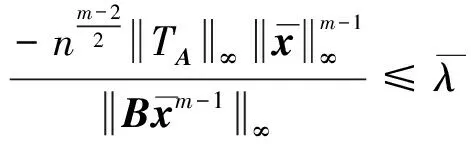
(10)

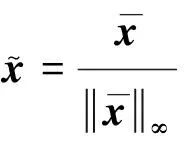
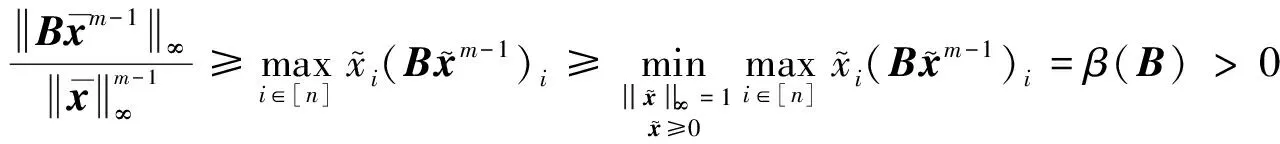
由上式和式(10)知，定理2的结论1中第一个不等式成立.

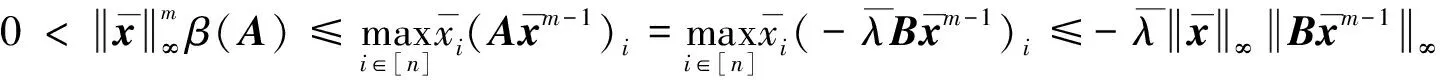
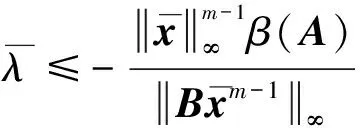
(11)

进一步，由于

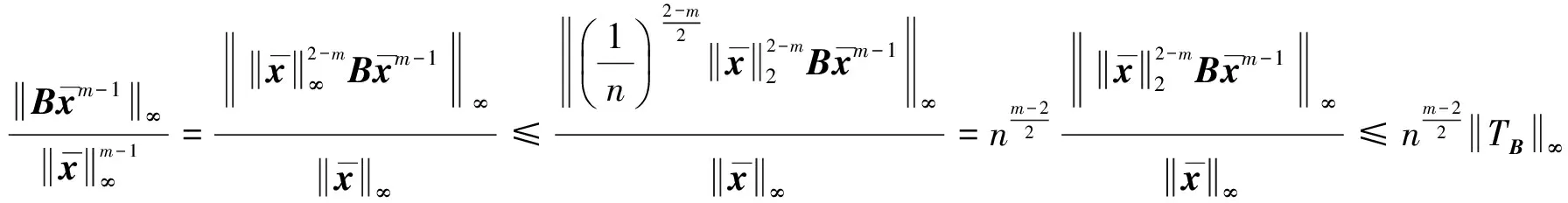
由上式和式(11)知，定理2的结论1中第二个不等式成立.从而定理2的结论1成立.

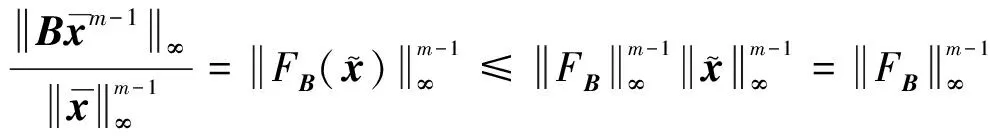
由命题3和定理2，可以得到下述推论.

推论2 设A,B∈Tm,n为严格半正，且B≥0,则：

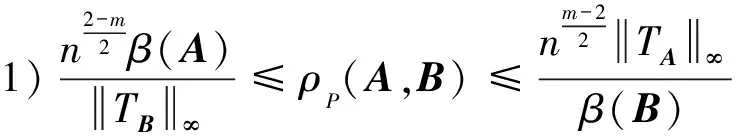
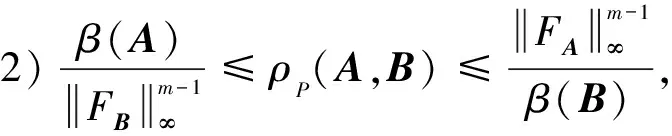
由引理2、引理3和推论2，进一步得到：

推论3 设A,B∈Tm,n为严格半正，且B≥0,则：

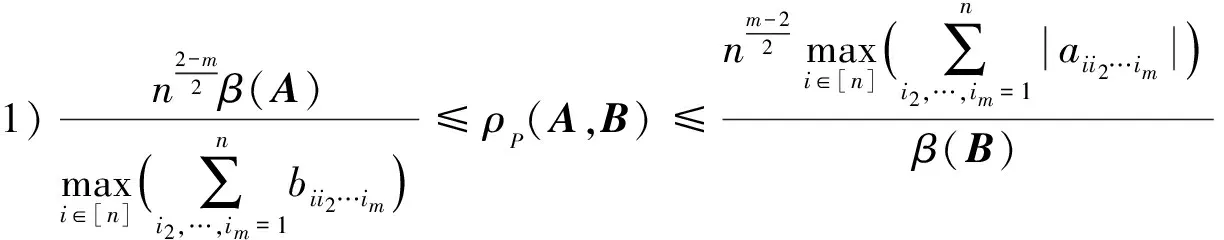
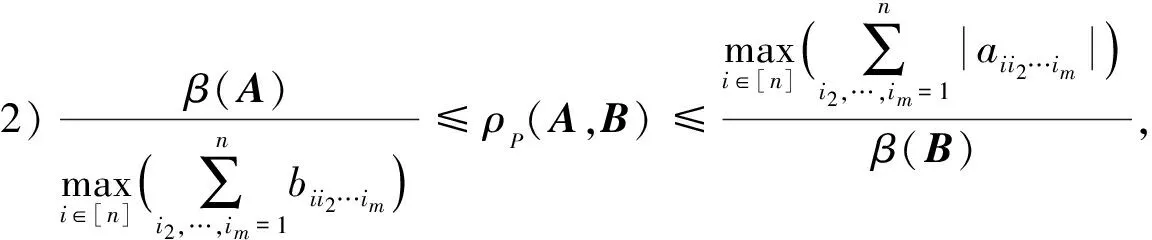
3 结束语

本文首先针对严格半正张量特征值互补问题，分别在B为负单位张量和非负严格半正张量的条件下，讨论了(A,B)的Pareto-特征值的符号特征.在此基础上，进一步得到了(A,B)的Pareto-特征值的上下界估计.这些结果为今后研究一般的(B无限制条件)严格半正张量特征值互补问题的Pareto-特征值的估计提供了新途径.

[1]LING C, HE H, QI L. On the cone eigenvalue complementarity problem for higher-order tensors[J]. Computational Optimization and Applications, 2016, 63(1): 143-168.

[4]QI L. Eigenvalues of a real supersymmetric tensor[J]. Journal of Symbolic Computation, 2005, 40(6): 1302-1324.

[5]LIM L H. Singular values and eigenvalues of tensors: a variational approach[C]// Proceedings of the 1st IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing,2005,1:129-132.

[6]HILLAR C J, LIM L H. Most tensor problems are NP-hard[J]. Journal of the ACM (JACM), 2013, 60(6): 45.

[7]SONG Y, QI L. Properties of tensor complementarity problem and some classes of structured tensors[J/OL]. Eprint Arxiv,2014, [2016-03-23]. http://arxiv.org/abs/1412.0113.

[8]QI L Q．Symmetric nonnegative tensors and copositive tensors[J]．Linear Algebra and its Applications, 2013, 439 (1):228-238.

[9]SONG Y, QI L. On strictly semi-positive tensors[J/OL]. Eprint Arxiv,2015, [2016-03-23]. http://arxiv.org/abs/1509.01327.

[10]SONG Y, QI L. Spectral properties of positively homogeneous operators induced by higher order tensors[J]. Siam Journal on Matrix Analysis and Applications,2013, 34(4): 1581-1595.

Pareto-spectrum Estimations of Eigenvalue Complementarity Problem with Strictly Semi-positive Tensors

LING Liyun, LING Chen

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

For a class of eigenvalue complementarity problem with strictly semi-positive tensors, we study the symbolic features of Pareto-eigenvalue. On this based, we obtain the upper and lower bounds of Pareto-eigenvalue for eigenvalue complementarity problem with strictly semi-positive tensors by using the constant definition and operator definition of strictly semi-positive tensors.

tensor; strictly semi-positive tensor; Pareto-eigenvalue; Pareto-spectrum

10.13954/j.cnki.hdu.2016.06.017

2016-04-19

国家自然科学基金资助项目(11571087)

凌莉芸(1991-)，女，河南洛阳人，硕士研究生，非线性优化.通信作者：凌晨教授，E-mail: macling@hdu.edu.cn.

O221.2

A

1001-9146(2016)06-0081-05