区间等式的可能度及其应用
2016-12-13汤立龙
汤立龙,李 炜
(杭州电子科技大学理学院,浙江 杭州 310018)
区间等式的可能度及其应用
汤立龙,李 炜
(杭州电子科技大学理学院,浙江 杭州 310018)
提出了区间等式的可能度定义,建立了该可能度的相关性质.讨论了新的可能度在求解含有等式约束的区间线性规划问题中的应用,避免了现有方法中需将等式约束化为两个不等式约束在计算上所带来的不便.最后给出了具体的算例.
区间数;可能度;区间线性规划
0 引 言
在区间数学的体系中,如何比较区间数的大小是一个关键问题.一个较为通用的方法是引入所谓的可能度来评判区间数的大小关系[1-2].但现在已有的文献都只考虑了区间不等式的可能度[3-6],而没有研究区间等式的可能度.本文将提出一种区间等式的可能度,给出其性质,并研究其在区间优化问题中的应用.
1 区间数相等的可能度定义
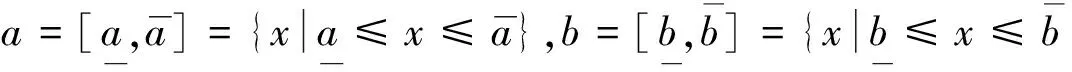
定义1 设区间数a,b满足ac=bc,且a,b至少有一个为非退化区间数,则称
(1)
为a=b的可能度.
2 可能度的相关性质
设区间数a,b满足ac=bc,且a,b至少有一个为非退化区间数,则a=b的可能度有如下性质:
性质1 0≤p(a=b)≤1
证明 显然
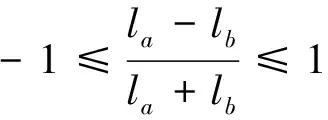
即有0≤p(a=b)≤1成立.证毕.
性质2 p(a=b)=p(b=a)
证明 容易看出

证毕.
性质3 p(a=b)=1的充分必要条件为a=b.
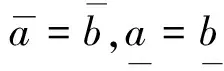
性质4 设区间数a,b不全为退化区间,则p(a=b)=0的充分必要条件为a,b有一个为退化区间.
小型无人机的应用,是以药物喷洒为前提起到相应的植保效果。而技术人员则以远距离压控为前提,对无人机高度加以调节,再按照农作物具体情况,对药物剂量、无人机高度和速度予以把控,以便将药液精准作用于农作物表面,还可借助旋翼下旋气流加快药液吸收、渗透[7]。

性质5 若p(a=b)=1,p(b=c)=1,则p(a=c)=1成立.
然而,一般的传递性不成立.
性质6 设α∈(0,1),若p(a=b)=α,p(b=c)=α,则p(a=c)≠α.
证明 α∈(0,1),这意味着a、b和c都是非退化的,下面分4种情况讨论.
1)当la 2)当la>lb>lc时,类似可证. 3)当la 4)当la>lb,lc>lb时,类似可证. 综上,当α∈(0,1)时,若p(a=b)=α,p(b=c)=α,则p(a=c)≠α.证毕. 现存的文献中只对区间不等式定义了可能度,而处理等式的方法则是转化其为一个规模更大的不等式系统.由于区间数学中所谓相依性的困难,这种转化往往是不可能的[7-8].即使能够转化,问题的规模也显著扩大.而借助于区间数等式可能度的定义,可以直接求解带等式约束的区间规划,避免了转化等式约束为不等式约束的麻烦. 引理 对两个区间数a,b.给定可能度水平λ(0<λ≤1),且ac=bc.则p(a=b)≥λ可转化为下述确定性约束 (2) 由引理得到: (3) 其中,xj≥0,j=1…n. 例 考虑下述区间线性规划问题: min[0.2,0.4]x1+[0.1,0.3]x2 s.t [0.1,0.2]x1+[0.4,0.5]x2=[0.2,0.3] x1,x2≥0. min Z=0.3x1+0.2x2 0.15x1+0.45x2=0.25 x1,x2≥0. 本文提出了区间数相等的可能度定义,并给出了其在求解带等式约束区间线性规划问题中的应用.要指出的是,本文中的方法并不局限于求解区间线性规划问题,也可以用于求解带区间等式约束的非线性规划问题以及区间非线性方程组的问题.求解非线性问题时,如何进行具体的区间模型的结构分解仍需进一步研究. [1]李炜,黄金花.区间系统与区间优化模型——理论与应用[J].南京信息工程大学学报(自然科学版),2016,9(1):23-33. [2]LI W, LIU X, LI H H. Generalized solutions to interval linear programmes and related necessary and sufficient optimality conditions[J].Optimization Methods & Software, 2015, 30(3): 516-530. [3]JIANG C, HAN X, LIU G R, et al. A nonlinear interval number programming method for uncertain optimization problems[J].European Journal of Operational Research, 2008, 188(1): 1-13. [4]达庆利,刘新旺.区间数线性规划及其满意解[J].系统工程理论与实践,1999(4):3-7. [5]NIRMALA T, DATTA D, KUSHWAHA H S, et al. Inverse interval matrix: a new approach[J].Applied Mathematical Sciences, 2011, 5(13): 607-624. [6]刘晓,李炜.区间线性规划最优解对应的约束矩阵的构造[J].杭州电子科技大学学报,2014,34(2):48-51. [7]HlAD1M. Weak and strong solvability of interval linear systems of equations and inequalities[J]. Linear Algebra and its Applications, 2013, 438(11): 4156-4165. [8]LI W.A note on dependency between interval linear systems[J].Optimization Letters, 2015, 9(4): 795-797.Possibility Degree of Interval Equation and Its Application TANG Lilong, LI Wei (SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China) The definition of the possibility degree of interval equality is proposed, and the related properties of the possibility degree are established. The new possibility degree application about interval linear program with equality constraints is discussed to avoid the difficulty of transforming equality constraints into two inequality constraints. An example is given to illustrate the method. interval number; possibility degree; interval linear programming 10.13954/j.cnki.hdu.2016.06.019 2016-05-17 国家自然科学基金重点资助项目(U1509217);浙江省自然科学基金资助项目(LY14A010028) 汤立龙(1991-),男,辽宁沈阳人,硕士研究生,数学规划.通信作者:李炜教授,E-mail:weilihz@126.com. O221 A 1001-9146(2016)06-0089-033 带等式约束的区间线性规划的可能度解法
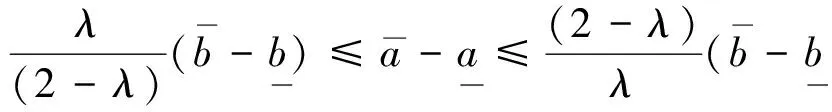
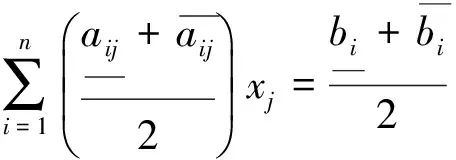
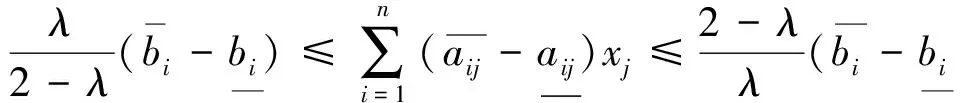
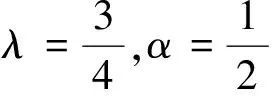
4 结束语
