有界对称域上Bergman空间Ap的乘子定理
2016-12-13张苏珍肖建斌姜佳梅
张苏珍,肖建斌,姜佳梅
(杭州电子科技大学基础数学研究所,浙江 杭州 310018)
有界对称域上Bergman空间Ap的乘子定理
张苏珍,肖建斌,姜佳梅
(杭州电子科技大学基础数学研究所,浙江 杭州 310018)
有界对称域上Hp(Ω)到lq(0 有界对称域;单位球;Bergman空间;乘子 在Hp空间理论中,文献[1]得到了2个定理:定理1证明了0 记Ω是Cn中包含原点的有界对称域,用b表示它的Silov边界.Ω相对于原点是圆型的和星型的,b也是圆型的.记Γ为Ω的全纯自同构群,Γ0表示Γ的使原点不变的子群,b上存在唯一的Γ0不变的测度σ,使得σ(b)=1. 在文献[2]中,华罗庚利用群表示的方法构造了一组齐次多项式: 复数序列空间lq(q>0)定义为 有关有界对称域上函数空间的讨论,有系列成果,详见文献[4-7]. 在定理的证明中要用到下面引理: 引理2 如果f∈Hp(Ω),0 引理3 设f∈H(Ω),0 (3) 与Boulanger推荐的用于砂土液化确定性分析的曲线相比,本文Logistic回归得到的表达式更为简单,结果也有所不同;具体而言,在qc1Ncs小于90时,Boulanger推荐的曲线要高于本文得到的液化概率50%的曲线;当qc1Ncs介于90到170之间时,该曲线介于本文得到的液化概率50%和30%曲线之间;本文得到的曲线简洁、可靠,工程应用中可根据工程要求选用合适的概率曲线。 令ρ→1时,r→1,得M1(r,f)≤c(1-r)-n(1/p-1)Mp(r,f).证毕. 定理1 设0 (3) (4) 则{λk}为Ap(Ω)到l∞的乘子.反之,对于Ω=Bn,式(4)也是必要条件. (5) 因为,Ap(Ω)为Banach空间(p≥1),或为Fréchet空间(0 (6) 本文得到了有界对称域上Bergman空间Ap(Ω)到lq(0 [1]肖建斌.有界对称域上Hp函数的系数乘子[J].中国科学(A辑),1995,25(1):12-21. [2]华罗庚.多复变数函数论中的典型域的调和分析[M].北京:科学出版社,1958:65-68. [3]HAHN K T, MITCHELL J.Hpspaces on bounded symmetric domains [J]. Transactions of the American Mathematical Society,1969, 146(2): 521-523. [4]史济怀.有界对称域上的Hardy-Littlewood定理[J].中国科学(A辑),1988,(4):366-375. [5]RUDIN W. Functions Theory in the Unit Ball ofCn[M]. New York: Springer-Verlag,1980:436. [6]罗罗,史济怀.Cn中有界对称域上不同加权Bergamn空间之间的复合算子[J].数学年刊,2000,21(1):45-52. [7]张学军,刘竟成.加权Bergman空间到μ-Bloch空间的复合算子[J].数学年刊,2007,28(2):255-266. Coefficient Multipliers of the Bergman Space on the Bounded Symmetric Domains ZHANG Suzhen, XIAO Jianbin, JIANG Jiamei (InstituteofFundamentalMathematics,HangzhouDianziUniversity,HangzhouZhejiang310018,China) The coefficient multipliers between Hardy spaceHp(Ω) andlq(0 bounded symmetric domains; unit ball; Bergman space; multiplier 10.13954/j.cnki.hdu.2016.06.018 2016-04-05 国家自然科学基金资助项目(11571104) 张苏珍(1990-),女,河南安阳人,硕士研究生,复分析.通信作者:肖建斌教授,E-mail:xjb@hdu.edu.cn. O174.5 A 1001-9146(2016)06-0086-030 引 言
1 预备知识

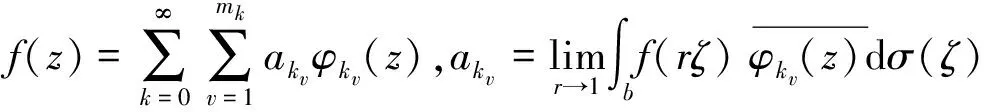
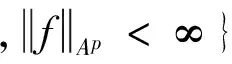
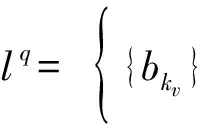

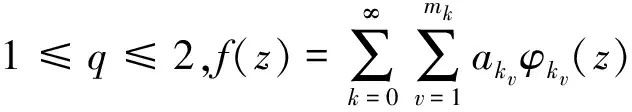



2 主要结果
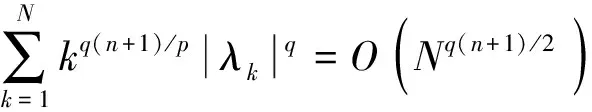
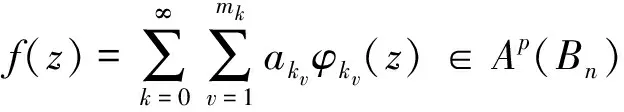
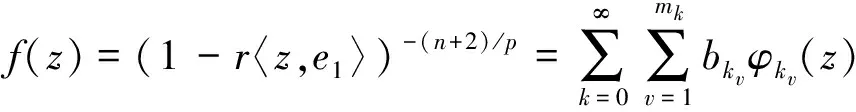

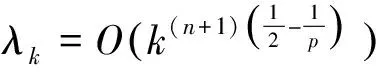
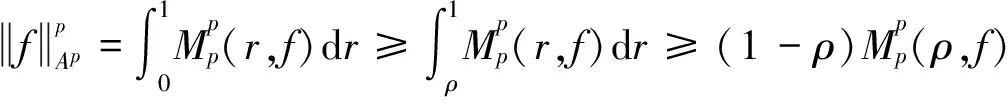
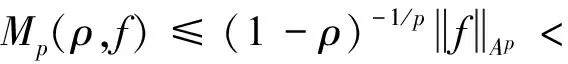
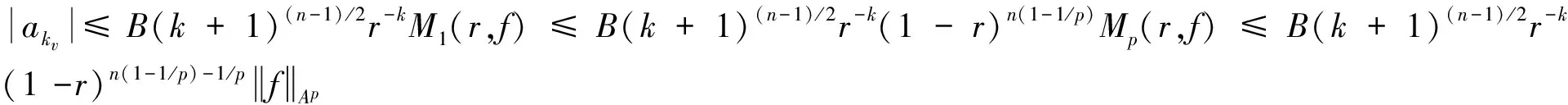
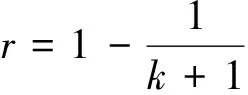
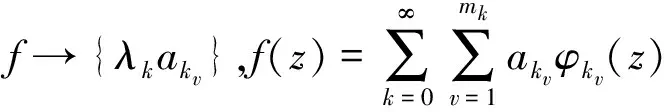
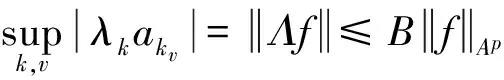
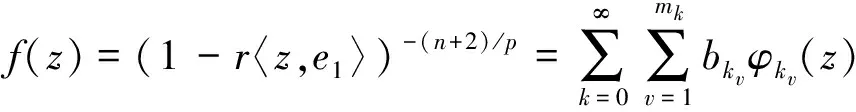
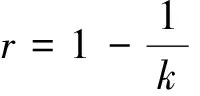
3 结束语
