一类新的3重量的二元线性码

蔡春彦，亓延峰

(杭州电子科技大学理学院，浙江 杭州 310018)



一类新的3重量的二元线性码

蔡春彦，亓延峰

(杭州电子科技大学理学院，浙江 杭州 310018)

线性纠错码在通信和计算机科学中有重要应用，也是密码理论与技术的重要工具，小重量的线性码可应用于认证码、秘密共享协议、结合方案中.如何构造新的具有好的参数的线性码是编码理论和应用的重要问题.该文考虑小重量码的构造，给出了一类3重量的二元线性码，并且确定了这类二元码的重量分布.

线性码；重量分布；迹函数；认证码；秘密共享协议

0 引 言

令q=2m，GF(q)表示含有q个元素的有限域，GF(q)*表示GF(q)的乘法群，其中m是正整数.一个[n,k,d]线性码C是GF(2)n上最小汉明重量为d的k维子空间，其中汉明重量是指码字的非零的元素个数.称C为最优线性码[1]，若二元线性码C的参数n，k和d满足线性码的某个界.一些最优线性码结果参见文献[2].令Ai表示线性码C中汉明重量为i的码字个数，线性码C的重量计数定义为1+A1z+A2z2+…+Anzn，重量分布(1,A1,…,An)是线性码理论的重要研究课题，可以使用某些算法来估计纠错能力和误差检测与校正的概率.t为(1,A1,…,An)中非零的Ai的个数，称线性码为t重量的线性码.

如何构造好的线性码是有意义的问题，一类重要的方法是使用函数来构造[3-6]，令F(x)∈GF(q)[x]，f(x)=Tr(F(x))，令D={x∈GF(q)*|f(x)=0}={d1,d2,…,dn}，则有码长为n的线性码CD={Tr(xd1),Tr(xd2),…,Tr(xdn))∶x∈GF(q)}，其中Tr为从GF(q)到GF(2)上的迹函数，称D为CD的定义集合，许多工作是使用不同函数来构造定义集合从而得到线性码CD[4-8]，例如F(x)=x2h+1，F(x)=x3+x,F(x)=x2,二次bent函数f(x),弱正则bent函数等.本文考虑使用函数F(x)=x2h+1+x来构造线性码，得到了3重量的线性码，这类线性码包含了文献[5]的线性码.

1 新的3重量二元线性码

本节使用新的函数F(x)=x2h+1+x来给出定义集合，从而构造了一类新的3重量二元线性码，并给出了这类线性码的相关参数和重量分布，具体证明在第2节中给出.

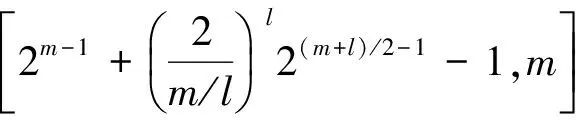
表1 定理1.1中的线性码的重量分布

例1.1 取(m,h)=(5,1)，则m/l=5，由定理1.1得到[11,5,4]线性码，其重量计数为1+9z8+16z10+6z12，此线性码是最优码，满足Griesmer界[2].

定理1.2 设m/l为偶数，当m≡2 mod 4时，线性码CD是[2m-1-1，m]二元码，其重量分布见表2；当m≡0 mod 4时，线性码CD是[2m-1-(-1)m/2l2m/2+l-1-1,m]二元码，其重量分布见表2.

表2 定理1.2中的线性码的重量分布

例1.2 取(m,h)=(6,1)，则m/l=6，m≡2 mod 4，由定理1.2得到[31,6,12]线性码，其重量计数为1+10z12+47z16+6z20.取(m,h)=(8,2)，则m/l=4，m≡0 mod 4，由定理1.2得到[95,8,32]线性码，其重量计数为1+10z32+240z48+5z64.

2 主要定理的证明

本节主要证明定理1.1及定理1.2，确定定理中线性码的主要参数和重量分布.为了更好地证明定理，首先做以下准备工作.

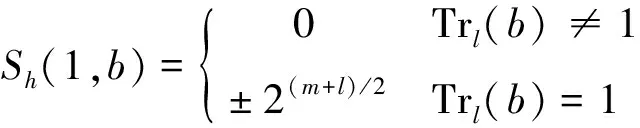
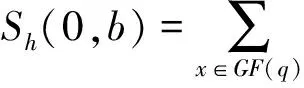
引理2.3 设m/l是偶数，b∈GF(q)*，m=2e.令f(x)=a2hx22h+ax∈GF(q)[x].

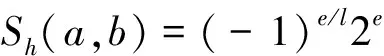
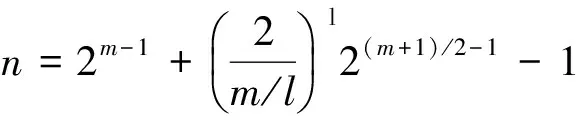
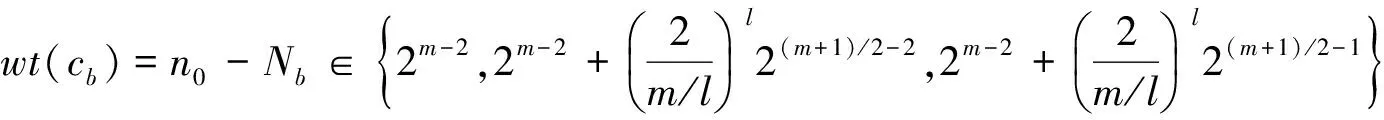
当m/l是偶数时，令m=2e，则Trl(1)=0.当m≡2 mod 4时，由引理2.3知，Sh(1,1)=0，线性码CD的长度n=n0-1=2m-1-1.由引理2.2和引理2.3，得到对任意的b∈GF(q)*，线性码CD码字cb的重量满足

wt(cb)=n0-Nb∈{2m-2,2m-2-2m/2+l-2,2m-2+2m/2+l-2}.

当m≡0 mod 4时，由引理2.3知，Sh(1,1)=-(-1)m/2l2m/2+l，线性码CD的长度n=n0-1=2m-1-(-1)m/2l2m/2+l-1-1.由引理2.2和引理2.3得，对任意的b∈GF(q)*，线性码CD码字cb的重量满足

wt(cb)=n0-Nb∈{2m-2,2m-2-(-1)m/2l2m/2+l-2,2m-2-(-1)m/2l2m/2+l-1}.

3 结束语

本文使用新的函数得到一类3重量的线性码.3重量的线性码可以产生结合方案.定义在有限域GF(p)上的线性码能够用来构造秘密共享协议和认证码.为了得到好的秘密共享协议，需要线性码C满足wmin/wmax>(p-1)/p，其中wmin和wmax表示最小和最大重量的线性码.易验证本文定理中的线性码满足wmin/wmax>1/2，可以构造秘密共享协议.如何使用一般的函数来构造新的、更好的线性码是以后的研究方向.

[1]HUFFMAN W C, PLESS V. Fundamentals of error-correcting codes[M]. Cambridge，U.K.: Cambridge University Press,2003:53-99.

[2]GRASSL M. Bounds on the minimum distance of linear codes. [EB/OL].[2016-02-23].http://www.codetables.de.

[3]LI C, YUE Q, LI F. Weight distributions of cyclic codes with respect to pairwise coprime order elements[J]. Finite Fields & Their Applications, 2014, 28: 94-114.

[4]YUAN J, DING C. Secret sharing schemes from three classes of linear codes[J]. Information Theory, IEEE Transactions on, 2006, 52(1): 206-212.

[5]XIANG C. Linear codes from a generic construction[J]. Cryptography and Communications, 2015: 1-15.

[6]DING K, DING C. A class of two-weight and three-weight codes and their applications in secret sharing[J]. Information Theory, IEEE Transactions on, 2015, 61(11): 5835-5842.

[7]ZHOU Z, LI N, FAN C, et al. Linear codes with two or three weights from quadratic bent functions[J]. Designs Codes and Cryptography, 2015: 1-13.

[8]TANG C, LI N, QI Y, et al. Linear codes with two or three weights from weakly regular bent functions[J]. Information Theory, IEEE Transactions on, 2016, 62(3): 1166-1176.

[9]LIDL R, NIEDERREITER H. Finite fields[M]. Cambridge，U.K.: Cambridge University Press, 1997:186-267.

[10]COULTER R S. On the evaluation of a class of Weil sums in characteristic 2[J]. New Zealand Journal of Mathematics, 1999, 28(2): 171-184.

[11]CALDERBANK A R, GOETHALS J M. Three-weight codes and association schemes[J]. Philips Journal of Research,1984,39(4): 143-152.

[12]LLOYD S P. Hamming association schemes and codes on spheres[J]. Siam Journal on Mathematical Analysis, 1980, 1(3): 488-505.

[13]CARLET C, DING C, YUAN J. Linear codes from perfect nonlinear mappings and their secret sharing schemes[J]. Information Theory, IEEE Transactions on, 2005, 51(6): 2089-2102.

[14]DING C, HELLESETH T, KLØV T, et al. A general construction of authentication codes[J]. Information Theory, IEEE Transactions on, 2007, 53(6): 2229-2235.

A New Class of Three-weight Binary Linear Codes

CAI Chunyan, QI Yanfeng

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Linear codes can be applied in consumer electronics, communication and data storage system. Linear codes with few weights are of important in secret sharing, authentication codes and association schemes. How to construct good linear codes is of interesting and important in coding theory and its application. This paper considers linear codes with few weights, presents a new class of three-weight linear codes, and determines parameters and weight distribution of these linear codes. Some of these linear codes are optimal.

linear codes; weight distribution; trace function; authentication codes; secret sharing schemes

10.13954/j.cnki.hdu.2016.06.021

2016-03-21

蔡春彦(1988-)，女，河北衡水人，硕士研究生，密码学.通信作者：亓延峰讲师，E-mail：qiyanfeng07@163.com.

TN911.22

A

1001-9146(2016)06-0096-04