钢管砼拱桥主拱圈交替吊装和分幅合龙中空间效应分析

李海军

（长沙理工大学土木与建筑学院，湖南长沙 410004）

钢管砼拱桥主拱圈交替吊装和分幅合龙中空间效应分析

李海军

（长沙理工大学土木与建筑学院，湖南长沙 410004）

钢管砼拱桥主拱圈常采用交替吊装、分幅合龙的施工方法，吊装过程中两幅拱肋间通过横向米撑连接成为一个空间体系，其理论线形与受力计算具有明显的空间效应特征。文中采用MIDAS／Civil有限元分析程序模拟实际施工工序对贵州省总溪河特大桥空钢管的成拱过程进行空间效应分析。结果表明，同一梁段左右幅的定位标高和扣索张拉力不同；先合龙幅的轴线偏位应先设置一定的预偏，以保证全部合龙后的轴线偏位正确回中；采用交替吊装、分幅合龙的钢管砼拱桥在空钢管成拱过程中的线形控制必须充分重视其空间效应，确保主拱圈合龙后的线形满足施工控制要求。

桥梁；钢管砼拱桥；交替吊装；分幅合龙；空间效应

钢管砼拱桥是一种自架设体系结构，结构刚度分阶段逐渐组合而成，体系灵活多变，能适应不同地质和地形条件，近年来在国内外得到广泛应用。施工控制是钢管砼拱桥建设中至关重要的一环，而主拱圈吊装过程中的空间效应分析是其中的关键，决定着主拱圈合龙后线形和受力是否满足设计要求。

目前对钢管砼拱桥主拱圈线形控制方法的研究主要集中在主拱圈平面线形控制上，极少考虑主拱圈的空间效应对线形控制的影响。文献［9］以铜汤（铜陵—汤口）高速公路太平湖大桥为工程背景，考虑到拱肋合龙时天气较恶劣、整个拱肋大悬臂时抗风稳定性较差，采用单边合龙的方法，降低了大悬臂施工风险，但也给整体结构性能带来一定的负面影响，主要原因是单边合龙后结构体系发生变化，两幅拱肋受力和变形特性不再对称。文献［10］以南浦大桥为工程背景，采用跨中预留间隙单边嵌入的合龙方式，即在两岸钢管桁架遵循上下游对称、两岸对称的原则，齐头并进安装完第五节段横撑后，上游先合龙，下游再采用同样的方式合龙。以上研究虽然都提及了主拱圈分幅合龙，但并没有对此过程中的空间效应进行详细阐述，而该问题在钢管砼拱桥施工控制过程中是不可回避的。该文以贵州省总溪河特大桥为工程背景，对主拱圈交替吊装、分幅合龙过程中的空间效应进行研究，为同类型桥梁施工控制计算提供参考。

1 空间效应分析

1.1 主拱圈交替吊装

主拱圈交替吊装是指先吊装某一幅的2个或更多节段再吊装另一幅的相应节段，然后在两幅拱肋间安装横撑，如此交替进行，直至主拱圈合龙。受主拱圈空间效应的影响，线形控制难度加大。施工过程中，左、右两幅同一节段因吊装顺序不同，理论线形会有所不同，原因是先吊装的拱段扣索力使主拱圈处于偏心受力状态，在其作用下主拱圈的标高和轴线会偏离理论位置，另一幅相应节段吊装完成后主拱圈才能处于平衡状态，标高和轴线也回到相应的理论位置。如图1所示，假设主拱圈已交替吊装至n-1节段，下一轮交替吊装n、n+1节段，施工步骤为左幅n节段→左幅n+1节段→右幅n节段

→右幅n+1节段→横向米撑。

图1 主拱圈交替吊装施工步骤示意图

交替吊装过程中由于空间效应而导致的第一个不同之处在于主拱圈各节段定位时标高和索力不同，标高决定索力，索力影响标高，二者一一对应，拱段定位时应以标高控制为主、索力控制为辅。利用MIDAS／Civil建立有限元分析模型模拟上述交替吊装过程，通过计算可得各节段定位时的索力与标高理论值（见表1）。

表1 各节段定位时索力与标高理论值

表1中 ，Fnz＞Fny，Fn+1z＞Fn+1y，Hnz＜Hny，H n+1z＜ Hn+1y，F‴nz=F′ny，F″n+1z=Fn+1y，H‴nz= H′ny，H″n+1z=Hn+1y，即同一节段因吊装顺序不同，控制索力和标高不同。

交替吊装过程中由空间效应导致的另一个不同之处是吊装过程中横向偏位的控制不同，主拱圈成拱后横向偏位是否满足设计要求，直接决定主拱圈的受力是否满足设计要求。左幅n节段吊装后，其扣索力水平分力相当于在主拱圈左幅施加水平荷载，该水平荷载相对于整个主拱圈来说为横向偏心荷载，主拱圈会产生向左的横向偏位。吊装左幅n+1节段时，由于左幅扣索力增大，这一横向偏位将继续增大。但随着右幅n、n+1节段吊装完成，右幅的扣索力水平分力会使整个主拱圈的水平荷载逐步回中，前一过程产生的横向偏位也自动归零。因此，在这个过程中，主拱圈出现的在允许范围之内的横向偏位无需调整，若强行将其调整至零偏位，则右幅n、n+1节段的吊装又将导致主拱圈出现向右的横向偏位。

1.2 主拱圈分幅合龙

钢管砼拱桥主拱圈分幅合龙是指主拱圈处于最大悬臂之前先单幅合龙再合龙另一幅。分幅合龙虽然可避免出现最大悬臂这一最不利状态，但会加大合龙难度。假设主拱圈左幅先合龙，各节段在其扣索力水平分力作用下会产生向左的横向偏位，分别为Δ1、Δ2、…、Δn，与交替吊装过程不同的是，合龙右幅时横向偏位Δ1、Δ2、…、Δn会有所减小，但不会全部为零，所以左幅合龙之前应对各节段横向偏位作适当调整。根据有限元模型分析结果，左幅合龙后再吊装右幅时，主拱圈各节段横向偏位的减小量分别为Δ′1、Δ′2、…、Δ′n，故左幅合龙之前各节段横向偏位调整量分别为Δ1-Δ′1、Δ2-Δ′2、…、Δn-Δ′n。可以通过风缆进行调节，待右幅合龙完毕后主拱圈回到理论位置。如果左幅合龙之前不对主拱圈横向偏位进行调整，则主拱圈全部合龙后各节段横向偏位不可能为零。

2 工程实例分析

2.1 工程概况

总溪河特大桥为杭瑞（杭州—瑞丽）高速公路贵州省境内的重要控制性工程，主桥采用跨径360 m上承式钢管砼变截面桁架拱，桥面宽度24.5 m，汽车荷载标准为公路-Ⅰ级，拱轴线采用悬链线，拱轴系数m=1.3，矢高h=69 m，矢跨比f=1／5.217。主拱圈采用等宽度变高度空间桁架结构，肋间设横撑和米撑。钢管拱肋对接接头采用管内法兰盘栓接、管外焊接的形式连接。主拱圈采用无支架缆索吊装千斤顶斜拉扣挂法施工，从拱脚至拱顶共划分为14个节段，全桥共58个节段。其立面布置见图2，横断面布置见图3。

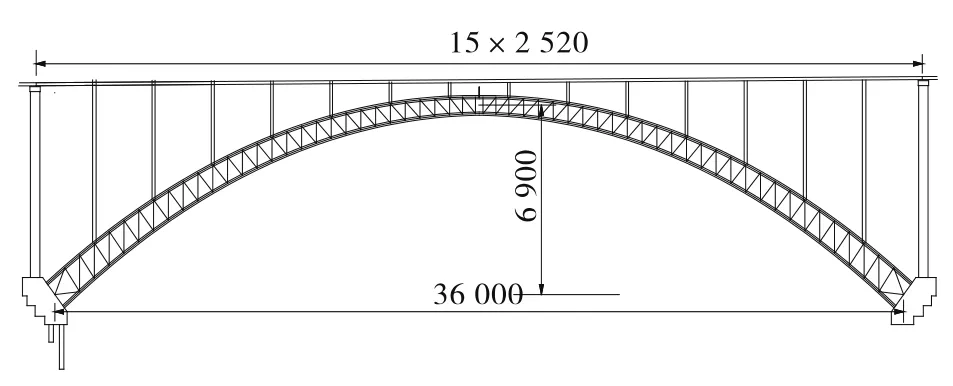
图2 总溪河特大桥立面布置（单位：cm）

2.2 有限元分析

主拱圈吊装过程中，为了实现工期目标，并考虑到吊装设备的限制，采用交替吊装、分幅合龙的方案，采用有限元平面杆系计算程序BDCMS结合MIDAS／Civil进行施工控制理论计算。主拱圈有限元计算模型如图4所示。

图3 总溪河特大桥横断面布置（单位：cm）

图4 总溪河特大桥主拱圈有限元计算模型

以毕节岸11＃、12＃节段吊装过程为例，通过有限元分析，这4个节段吊装时，受主拱圈空间效应的影响，不同工况下同一节段的索力和标高理论值各不相同（见表2）。

由表2可知：同一节段由于吊装顺序不同，受主拱圈空间效应的影响，定位时的索力和标高会有所差异。右幅11＃节段和左幅11＃节段相比，索力小18.7 k N，标高高12 mm；右幅12＃节段与左幅12＃节段相比，索力小19 k N，标高高11 mm。11＃、12＃节段全部吊装完成后，主拱圈处于平衡状态，同一节段索力和标高相等。然后安装横向米撑，完成一个完整的交替吊装过程。如此循环，完成整个主拱圈的施工。

若在上述吊装过程中忽略主拱圈空间效应的影响，对同一节段采用相同的索力和标高进行控制，各节段的索力和标高见表3。

表2 考虑主拱圈空间效应时毕节岸11＃、12＃节段吊装时各节段索力和标高

表3 忽略主拱圈空间效应时毕节岸11＃、12＃节段吊装时各节段索力和标高

由表3可知：对于同一节段，如果不考虑主拱圈空间效应的影响，采用相同的索力和标高进行控制，必然会导致吊装完成后主拱圈两幅标高和索力均不对称。右幅11＃节段与左幅11＃节段相比，索力大18.7 k N，标高低12 mm；右幅12＃节段与左幅12＃节段相比，索力大19 k N，标高低11 mm。这将给后续工序的施工带来困难。

毕节岸11＃、12＃节段吊装过程中，由左幅11＃、12＃节段扣索力水平分力引起的主拱圈横向偏心荷载导致主拱圈各节段出现表4所示横向偏位。

根据以上分析，右幅11＃、12＃节段吊装完成后，主拱圈总的扣索水平力横向对称，各节段横向偏位为零，在左幅12＃节段吊装后如出现表4所示横向偏位，则不需要调整。若强行将各节段横向偏位调整到零，则右幅11＃、12＃节段的吊装又会使主拱圈各节段出现向右的横向偏位，反而会使最终的横向偏位不居中，带来额外的轴线偏差。

表4 左幅12＃节段吊装后各节段横向偏位mm

主拱圈交替吊装至12＃节段后，采用分幅合龙的方案进行合龙，先吊装右幅13＃、14＃节段并合龙，且右幅合龙之前对主拱圈各节段横向偏位进行调整，因为右幅合龙后主拱圈体系发生变化，左幅13＃、14＃节段的吊装无法完全消除主拱圈各节段的横向偏位。通过有限元分析，右幅合龙之前各节段的横向偏位见表5，左幅14＃节段吊装后各节段的横向偏位改变量见表6，由此可计算出右幅合龙之前主拱圈各节段的横向偏位调整量（见表7）。各节段横向偏位可通过风缆进行调节。

表5 右幅合龙前各节段横向偏位mm

表6 左幅14＃节段吊装后各节段横向偏位改变量mm

表7 右幅合龙前各节段横向偏位调整量mm

综上所述，总溪河特大桥分幅合龙过程中，右幅合龙前主拱圈各节段横向偏位应按表5所示理论值进行控制，然后在风缆调节时按表7所示进行调整，最终左幅合龙后主拱圈的轴线才能顺利居中。

3 结论

（1）钢管砼拱桥主拱圈在采用交替吊装施工方法时会呈现明显的空间效应特征，左、右幅同一节段在安装定位时的标高和索力理论值不同，在进行线形控制时需充分考虑主拱圈空间效应的影响，对左、右幅相同节段采用不同的理论值进行精确定位。

（2）主拱圈交替吊装过程中，单幅先吊装节段的扣索力会产生横向偏心水平荷载，使主拱圈产生轴线偏差，对于该轴线偏差不需进行额外调整，在另一幅相应节段吊装并索力张拉到位后轴线偏差会自动归零。

（3）主拱圈交替吊装和分幅合龙时，由于单幅合龙后主拱圈体系改变，单幅合龙前的横向偏位不能像悬臂拼装时一样不作调整，而需准确计算出另一幅的吊装对先吊装一幅所带来的轴线变化，然后确定单幅合龙前各节段横向偏位的调整量，并采用风缆进行调整，这样才能使最终合龙后的主拱圈横向偏差归零。

［1］ 郝聂冰，张雪松，唐鹏胜，等.大跨径钢管混凝土拱桥吊装线形控制方法研究［J］.中外公路，2013，33（3）.

［2］ 涂光亚，卢伟升，张克波，等.大跨度钢管混凝土拱桥拱肋吊装的线形控制［J］.公路交通科技：应用技术版，2007（1）.

［3］ 顾颖，姚昌荣，李亚东，等.大跨度钢管混凝土拱桥安装线形控制方法研究［J］.桥梁建设，2014，44（1）.

［4］ 郝聂冰，顾安邦.500 m级钢管混凝土拱桥施工控制［J］.西南交通大学学报，2015，50（4）.

［5］ PMata，S Oller，AH Barbat.Static analysis of beam structures under nonlinear geometric and constitutive behavior［J］.Computer Methods in Applied Mechanics and Engineering，2007，196（45）.

［6］ 霍庆杰.钢管混凝土拱桥施工监控技术研究［D］.石家庄：河北科技大学，2012.

［7］ 周建超.吊装工艺下钢管混凝土拱桥施工控制关键技术研究［D］.成都：西南交通大学，2013.

［8］ 刘新根.钢管混凝土拱桥拱肋吊装及注浆力学仿真分析［J］.世界桥梁，2014，42（4）.

［9］ 姚运昌.大跨度钢管混凝土拱桥施工控制研究［D］.合肥：合肥工业大学，2007.

［10］ 张冶成.大跨度钢管混凝土拱桥施工控制研究［D］.杭州：浙江大学，2004.

［11］ 袁海庆，范剑锋，范小春.钢管混凝土拱桥拱肋吊装过程的线形优化方法［J］.武汉理工大学学报，2002，24（2）.

U448.22

A

1671-2668（2016）06-0203-04

2016-03-22