Esscher保费的非参数估计

张林娜，温利民,2

（1.江西师范大学 数学与信息科学学院，南昌 330022；2.江西财经大学 信息管理学院，南昌 330013）

Esscher保费的非参数估计

张林娜1，温利民1,2

（1.江西师范大学 数学与信息科学学院，南昌 330022；2.江西财经大学 信息管理学院，南昌 330013）

Esscher保费原理是非寿险精算中最重要的保费原理之一,在精算学中有重要的运用。文章研究了Esscher保费的非参数估计,并证明了估计的强相合性和渐近正态性，最后通过数值模拟的方法验证了估计的收敛速度及渐近正态性。

Esscher保费原理；非参数估计；相合性；渐近正态性

0　引言

一般地,保险公司常常根据已有的历史数据来制定保费。在保险精算学中,把一份保单可能导致的索赔定义为一个风险,用随机变量X来表示。因此,X为只取非负值的随机变量,这时该保险的历史索赔数据Xi，i=1，2，…可以看作是该总体的随机样本。通过分析和了解这些数据信息,进而为该保单制定合理的价格,即为保费。有关保费的厘定可参考文献[1]和文献[2]。在某种保费原理下,通过样本对保费进行估计,可分两种情况,一种情况是已知风险X的分布类型,但分布中含有未知参数,因此通过样本信息对未知参数进行估计,进而对保费进行估计,这类估计方法为参数估计法,另一种情况是我们对风险的分布一无所知,可用经验分布对总体分布进行估计,这种方法称为非参数估计。对于Esscher保费的参数估计,我们有多种方法对其进行估计,例如极大似然估计、矩估计、Bayes估计、信度估计等,可参考文献[3-5]。然而在实际生活中,我们很难得知风险的真实分布,因此,对Esscher保费非参数估计问题的研究也很重要。

1　Esscher保费原理

考虑某个保险公司的某种保单在一定时间（这里指一年）的索赔额,一般地,对索赔额过程Xi，i=1，2，…提出下面的假设：

假设1：索赔额Xi，i=1，2，…独立同分布,具有概率分布函数密度函数矩母函数以及和都存在。

根据假设,对Esscher保费的定义如下：

定义1：对随机变量X,定义X的保费为：

在Esscher保费原理中,h被称为Esscher参数。容易验证也就是说,根据Esscher保费原理收取的保费能保证偿付。由于Esscher保费是h的函数,可以证明Esscher保费是 h的递增函数,且有因此,当h增大时,保费的安全负荷系数增加,但被保险人承担的保费压力也较大,保险公司可以根据自身的业务情况决定一个合适的Esscher参数。另外,Esschcr保费事实上是使得期望指数损失函数达到最小的解,可参考文献[5],即：

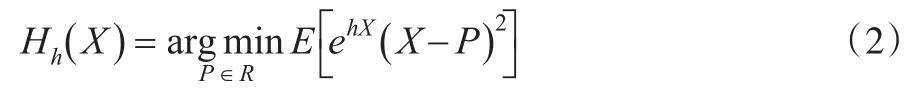
2　Esscher保费的非参数估计

本节给出Esscher保费的非参数估计及其大样本性质。设Xi,i=1，2，…，n为来自总体X的样本容量为n的样本,即为前n年的历史数据,若用Plug-in估计去估计总体X的分布,则可得到的一个非参数估计：

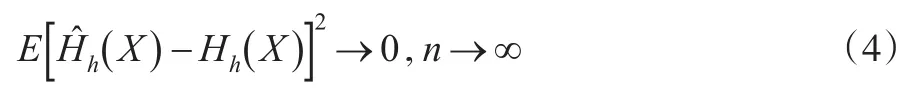
证明：由式(3)可知

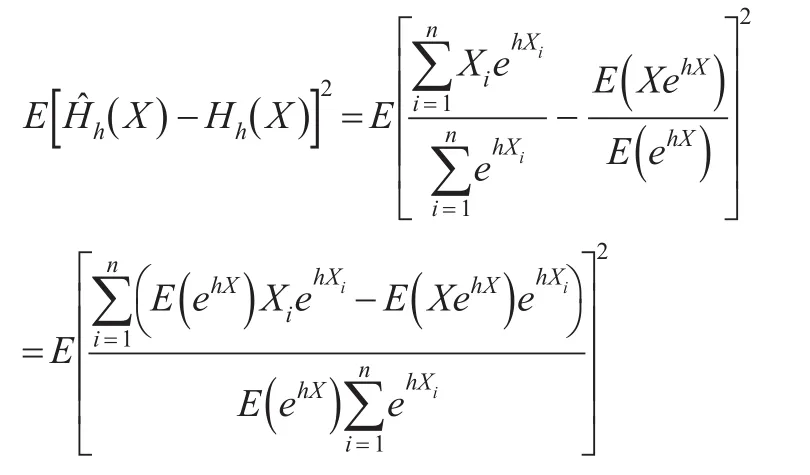
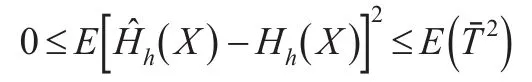
证明：为了方便,本文令：

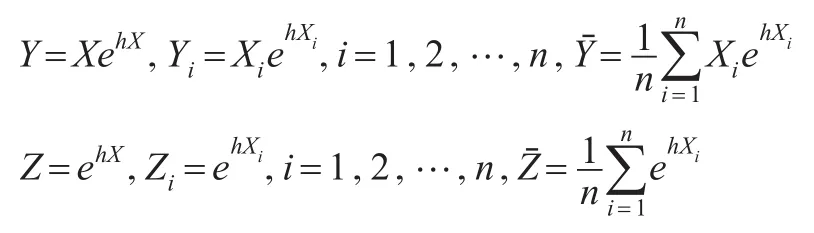
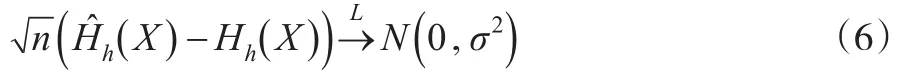
其中：

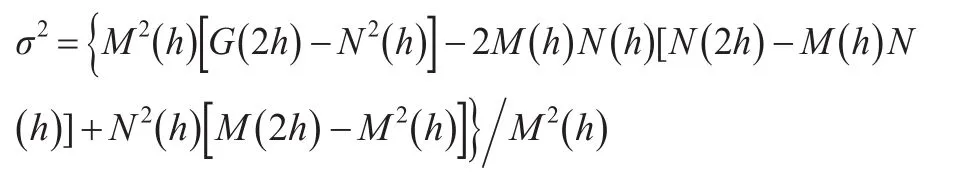
证明：本文仍用定理2的记号,并令:

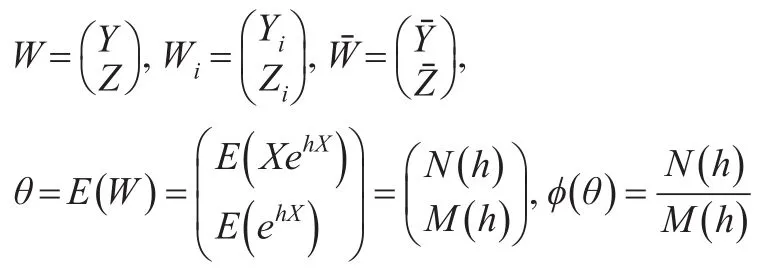
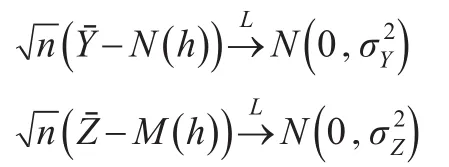
其中：

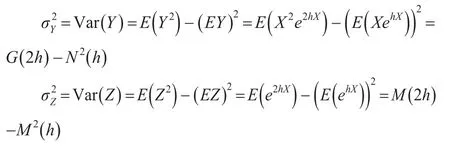
同理,可计算Y及Z的协方差为：

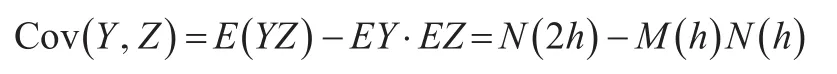
由于{} Wi，i=1，2，…，n也为独立同分布的二维随机向量,因此由中心极限定理,有：

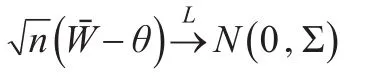
其中Σ为向量W的协方差阵：

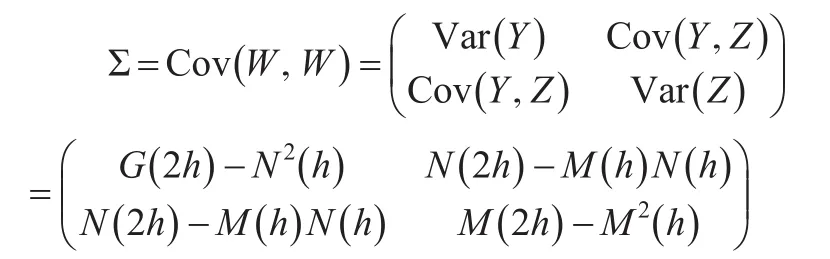
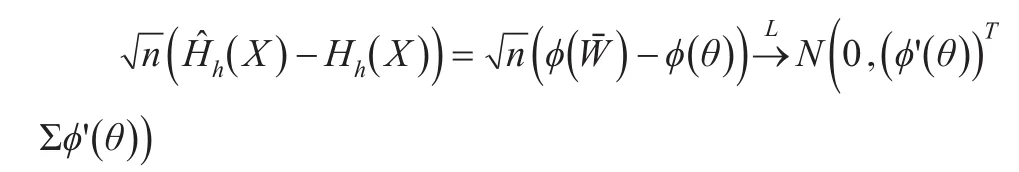
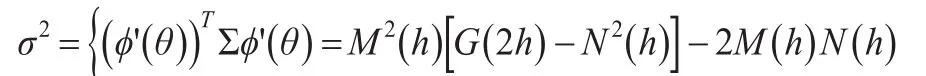
3　数值模拟

本文在例1给定的分布假设下进行数值模拟,验证Esscher保费的非参数估计的大样本性质,并与极大似然估计(MLE)进行比较。Esscher保费的MLE也即将分布中未知参数的MLE代入式(1)即可。在例1中,Poisson分布的参数λ的极大似然估计为则在Poisson分布下,Esscher保费的MLE为本文运用Bootstrap方法进行数值模拟,比较非参数估计与MLE在不同样本容量下的均方误差,均方误差的预测可分别用下面的式子近似,记为MSEP：

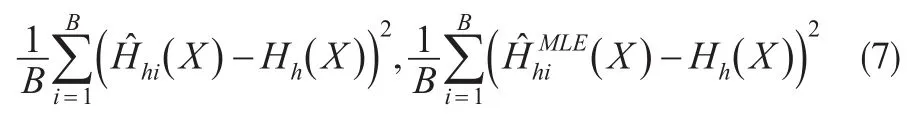
分别取n=30，100，200，500，800，1000下模拟,每次模拟重复5000次,计算得到两种估计的平均值及其相应的预测均方误差MSEP如表1所示。

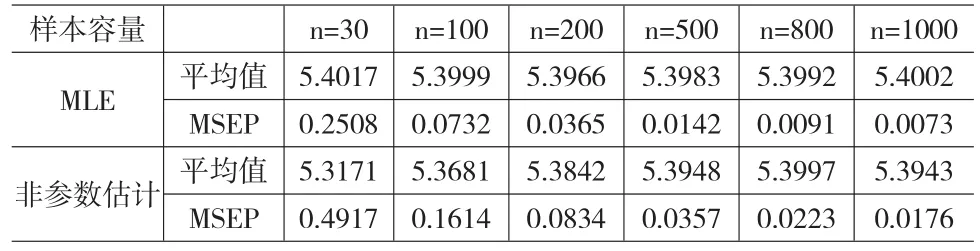
表1　不同样本容量下,MLE及非参数估计的均值和预测均方误差

由表1可看出在不同的样本容量下,两种估计的平均值与真实值都较接近,且随着样本容量n的增大,MSEP都较小,并且越来越小,同时也可看出非参数估计的MSEP略大于极大似然估计的MSEP,但在实际生活中,我们很难从已有的数据得知总体的分布类型,若分布判断错误,可能造成很大的估计误差,由表1可看出非参数估计的预测均方误差也较小,因此,Esscher保费的非参数估计也是一个很好的估计。

[1]Young V R.Premium Principles[M].New Jersey:Wiley,2004.

[2]Furman E,Zitikis R.Weighted Premium Calculation Principles[J].In⁃surance:Mathematics and Economics,2008,42(1).

[3]Pan M,Wang R,Wu X.On the Consistency of Credibility Premiums Regarding Esscher Principle[J].Insurance:Mathematics and Econo⁃ics,2008,42.

[4]Strasser H.Consistency of Maximum Likelihood and Bayes Estimates[J]. The Annals of Statistics,1981,9(5).

[5]王伟,温利民,章溢.Esscher保费原理下信度估计的比较[J].华东师范大学学报(自然科学版),2010,(3).

（责任编辑/易永生）

O211.9

A

1002-6487（2016）22-0018-03

国家自然科学基金资助项目（71001046）；江西省教育厅基金资助项目（GJJ13217）；江西省研究生创新基金项目项目（YC2014-S162）

张林娜（1991—），女，山西大同人，硕士，研究方向：数理统计、保险精算。温利民（1979—），男，江西石城人，博士，教授，研究方向：数理统计、保险精算。