“古典型”地区间投入产出模型:基础框架及其比较
2016-12-10丛建辉刘庆燕李文举
丛建辉,刘庆燕,李文举
(山西大学经济与管理学院,太原030006)
“古典型”地区间投入产出模型:基础框架及其比较
丛建辉,刘庆燕,李文举
(山西大学经济与管理学院,太原030006)
地区间投入产出模型在产业关联与跨区域绿色核算等领域发挥了独特作用,受到理论界日益密切的关注。文章重点阐述了Isard模型、Chenery-Moses模型、Riefler—Tiebout模型、Leontief模型、Leontief—Strout模型等五种“古典型”地区间投入产出模型的基础数理框架,并系统比较了各模型的优劣势及适用性。
地区间投入产出模型;Isard模型;Chenery-Moses模型
0 引言
地区间投入产出模型是由各区域投入产出模型联结而成、衡量不同区域之间互动关系的数理工具。早在20世纪50、60年代即出现了构造地区间投入产出模型的理论框架,但由于该类模型的构建需要耗费大量的时间与人力、物力,因此地区间模型研制的进展非常缓慢,在70年代后渐趋停滞,相关的应用研究也多局限在区域之间的产业关联测度方面。然而,随着全球环境与气候变化问题日益凸显并作用于区域层面,地区间投入产出模型由于能够测度生态足迹、贸易隐含碳排放以及碳泄漏等跨区域绿色核算问题,重新受到了理论界的密切关注[1,2]。
各种具体模型的构建依赖于地区间投入产出模型的基础模型,而对真实区际贸易联系情况的不同简化处理方式,导致了地区间投入产出基础模型类型上的多样化。根据估算方法的不同,地区间投入产出基础模型可分为“古典型”模型和现代方法模型两类。现代方法模型基于统计推断与信息理论的方法估算地区间贸易流量,运用了相对复杂的数学方法,目前尚未大规模运用,而“古典型”模型的理论框架相对成熟,应用更为广泛。
本文主要阐述Isard模型[3]、Chenery-Moses模型[4,5]、Riefler-Tiebout模型[6]、Leontief模型[7]、Leontief-Strout模型[8]这五种“古典型”地区间投入产出模型的基础框架并对各模型进行系统的比较分析,以进一步推进地区间投入产出表的研制工作,为该类模型的后续研究及其在实践层面的应用提供有价值的参考。与已有研究相比,本文的特色之处在于:(1)所囊括的模型更为全面,除了行系数模型与阿柴尔特模型没有分析外,对五种主要“古典型”地区间投入产出模型都进行了论述;(2)系统评价并比较了五种模型的优劣势与适用性。
1 主要的地区间投入产出模型
出于简化分析过程的考虑,下文对Isard模型、Chenery-Moses模型均以两地区模型为例进行说明,即假设只存在两个有贸易往来的地区r与地区s,两地区各部门之间生产要素自由流动,通过两地区模型得到的基本原理与结论可以任意推广到多地区,只是在数据处理量上大幅增加;Riefler-Tiebout模型在两地区之外,加上“世界其他地区”后,变成三地区模型,但分析结构与上述两地区模型基本相同;而对Leontief模型与Leontief-Strout模型的处理,仍然建立在多地区的基础之上。另外需要指出的是,各模型数学表达式中凡需要用特定矩阵的逆矩阵求解的,其原矩阵都为可逆矩阵,本文略去了其证明过程。
1.1Isard模型
Isard模型是第一个较为系统且产生广泛影响力的地区间投入产出模型,又称为区域间投入产出模型(Interregional input-output model,IRIO模型),由区域经济学家Isard于1951年初步建立,1960年完善。该模型是一个输入非竞争型模型,认为不同地区的同一产品也存在差异,相互之间不能替代。
1.1.1Isard模型的基本框架
对单一地区来说,一般的投入产出模型投入产出式基本结构为:
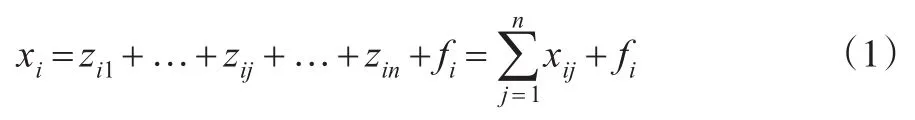
xi为所研究区域i部门产品的总产出,zij为该地区j部门使用i部门产品的数量(或价值),fi表示该地区对i部门产品的最终需求量。式(1)表示某一地区i部门产品的产量等于该部门产品用作该地区其他各部门产品中间投入的使用量及作为本地区最终产品的消耗量。
在地区间模型中,需要对商品流量按区域进行划分,如在两地区模型下,地区r与地区s之间有产品的流动。根据式(1),r地区第i个部门有如下方程式:
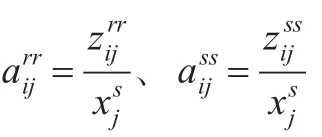
记分别为r地区与s地区的直接消耗系数(技术系数),Arr、Ass为其矩阵形式;而
分别为各自的地区间直接消耗系数,Ars、Asr为其矩阵形式。将各种直接消耗系数代入式(2),可得:
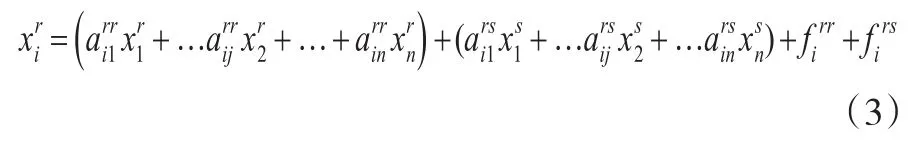
表示成矩阵形式为:

S地区投入产出表达式结构与之类似,为:

对式(4)和式(5)移项并合并同类项,有:
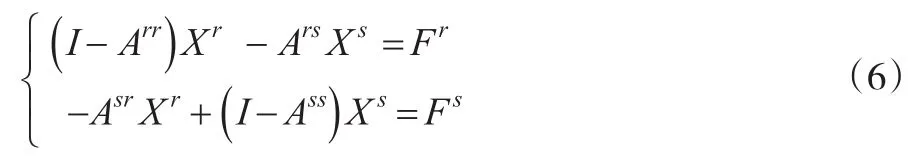


式(8)即为Isard模型的一般表达式。
1.1.2对Isard模型的评价
Isard模型通过直接消耗系数矩阵完全区分了各种贸易模式的来源地、目的地及其具体部门,以直接消耗系数分块矩阵的主对角线矩阵来反映区域内部经济结构,而以非对角线矩阵来反映区域之间的经济联系。由于其较为完美的阐述了两个地区的贸易模式,因此被称为“理想的”(ideal)地区间投入产出模型。该模型首次提出了“可贸易性”(tradability)这一概念,不具有可贸易性特征的一些产品部门被从分析中剔除,与直接调查法相比,该模型精简了一些程序,可操作性得到加强。
尽管如此,该模型对数据的需求仍然巨大,需要编制地区间投入产出系数矩阵,除了动用大量的人力、物力和时间投入外,数据的精确性也不能保证。另外,该模型内在要求地区内直接消耗系数和地区间直接消耗系数都要保持稳定,这意味着各区域内的生产结构和区域间贸易结构被“冻结”。在区域经济联系发生变化的情况下,研究者无法确认这种变化是因为生产技术原因引起还是因为贸易结构原因引起。
1.2Chenery-Moses模型
作为对Isard模型的一种简化,Chenery和Moses在对意大利与美国区域经济的研究中分别独立提出了具有相似结构的多区域投入产出模型(Multiregional Input Output Model,MRIO),又称为列系数模型。该模型属于输入竞争型模型,假设不同地区的同一产品完全同质。
1.2.1Chenery-Moses模型的基本框架
仍然假设存在两个地区r与s,Chenery-Moses模型中i部门产品的流动情况,如表1所示:

表1 部门i产品在两地区间流动矩阵
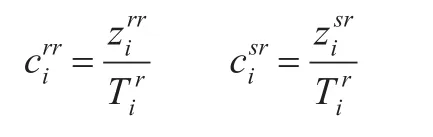
Chenery-Moses模型按照式(3)的形式可表示为:
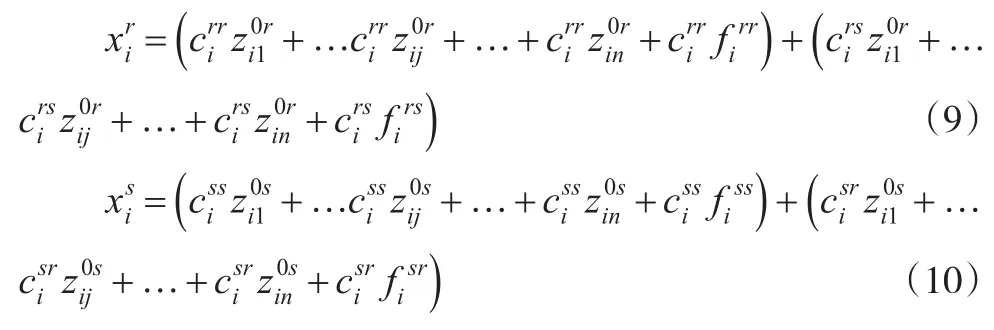
将直接消耗系数代入式(9)和式(10),有:
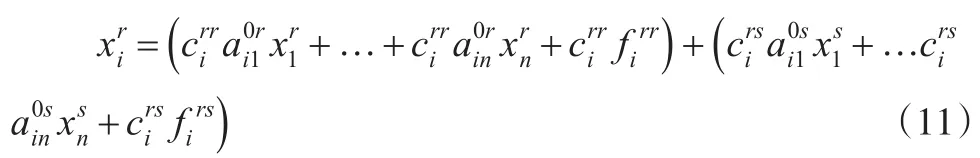
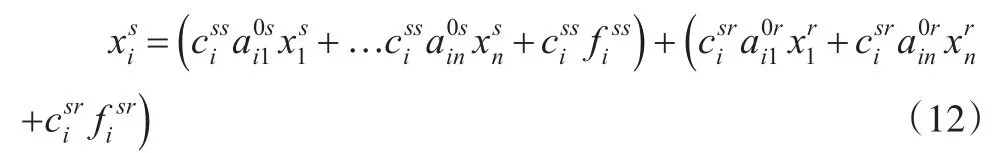
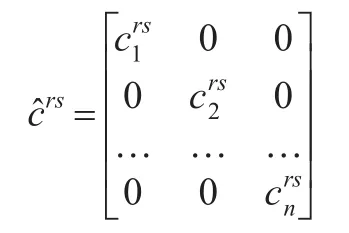
则式(11)和式(12)转换后矩阵形式为:
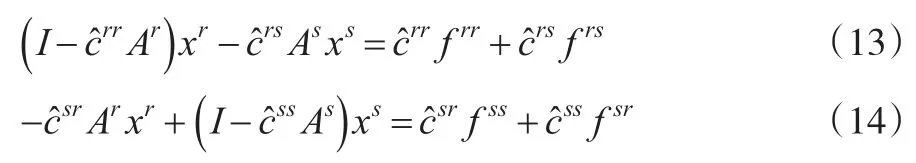

转化为逆矩阵形式:

根据式(16),如果已知贸易系数矩阵C和直接投入系数矩阵A,就可以根据规划期的最终需求目标,预测各地区产量。因此运行一个完整的Chenery-Moses模型核算体系,需要两套基本的数据:一套各个地区的投入产出表和一套地区间流量表。
1.2.2对Chenery-Moses模型的评价
如上文分析,Chenery-Moses的重要假设是:一个地区生产某种产品的技术只取决于特定部门的投入,而与投入部门所在区域无关。尽管该假设并不完美,但具有统计上的可行性。另外,它区分了直接消耗系数()与贸易系数(),所以可以分别衡量产品技术的提高和贸易模式的改变所产生的不同影响,但其也存在一些显而易见的缺陷,比如“流入比例假定”这一核心假设就与真实世界的区域贸易关系有一定差距。
1.3Riefler-Tiebout模型
建立于1970年的Riefler-Tiebout模型同样是Isard模型的一种简化形式,主要适用于两个区域(加上世界其他地区)的情况。在估算同一区域的商品流量时,该模型与Isard模型类似,需要编制详尽的地区内部投入产出矩阵,而对于区域之间的商品流量,该模型的处理方法与Chenery-Moses模型相近,采用估算方式。
1.3.1Riefler-Tiebout模型的基本框架
在Riefler-Tiebout模型框架中,r地区i部门产品的产量与式(2)一致,只不过纳入了世界其它地区的中间需求和最终需求变量。
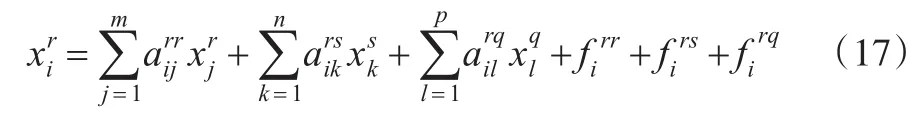

其中ART表示该模型的直接消耗系数矩阵。与Isard模型相比,Riefler-Tiebout模型的不同之处在于其地区间直接消耗系数矩阵的决定方式有所不同。
在对地区间贸易的处理上,该模型与Chenery-Moses模型思想相似,试图回避Isard模型中过多的数据需求。不过Riefler与Tiebout对Chenery-Moses模型的“流入比例假定”提出了质疑。一般而言,投入产出模型中的部门是按照产品异质性进行分类的,不同的产出部门在进口投入品方面通常会表现出不同的特性,所以“流入比例假定”与事实并不相符,这一情形也得到了实际调查数据的支持。
在他们的模型中,假定来自于特定地区的投入品与世界其他地区的投入品比值是一个常量,这一比值用输出贸易系数表示,代表r地区i部门产品出口到s地区的数量与s地区i部门产品总进口的比例,该比例可用贸易统计数据进行估算。
引入输出贸易系数后,地区间的直接消耗系数矩阵可以表示成如下形式:

1.3.2对Riefler-Tiebout模型的评价
Riefler-Tiebout模型舍弃了“流入比例假定”,这也就意味着对r地区来说,各部门来自于本区域和特定地区s的投入品比例是不固定的,但在r地区的所有进口投入品中,来自于特定地区s的比例是固定的。该模型试图在Isard模型与Chenery-Moses模型之间形成一种折中,寻求在尽量保留Isard模型精确度的前提下,以更少的数据和简化的贸易系数提高其可操作性。
尽管从形式上看来,该模型兼具Isard与Chenery-Moses两种模型的优点,但其能够成功运行的前提是存在一个地区的进口和出口贸易矩阵及相关的其他贸易统计数据,这在现实操作层面难度较大。
1.4Leontief模型
Leontief模型于1953年提出,也称为国内投入产出模型(intranational input-output model)或平衡区域模型(balanced regional model)。Leontief模型的基本设定是:在一个国家经济体中,不同的商品有不同的市场范围,一些商品的生产和消费在国家层面上平衡,如飞机制造、农业,而另一些商品则在地区层面上实现了供需相等,如地区性公用事业、房地产、个人修理类服务(如理发)等。在该模型中,需要按市场导向清晰划分两种产品类型。
1.4.1Leontief模型的基本框架
该模型的数学结构与Isard模型基本相同,但对每个部分的解释完全不同。
设有n种产品,其中地区性产品类别为1,2,…h,全国性产品类别为h+1,h+2,…n,这种产品类别的划分是事先给定的;直接消耗系数与国家投入产出表获得的数据一致,并且在各个地区都相同;国家和地区部门的总产出(XR、XN)及最终需求数据(fR、fN)外生给定。
其直接消耗系数矩阵为:
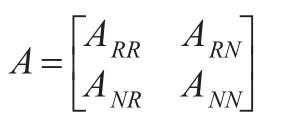
需要指出的是,这里的下标R与N并不代表具体的部门,而是分别指代地区性产品和全国性产品。类似Isard模型的运算过程,有如下平衡关系:
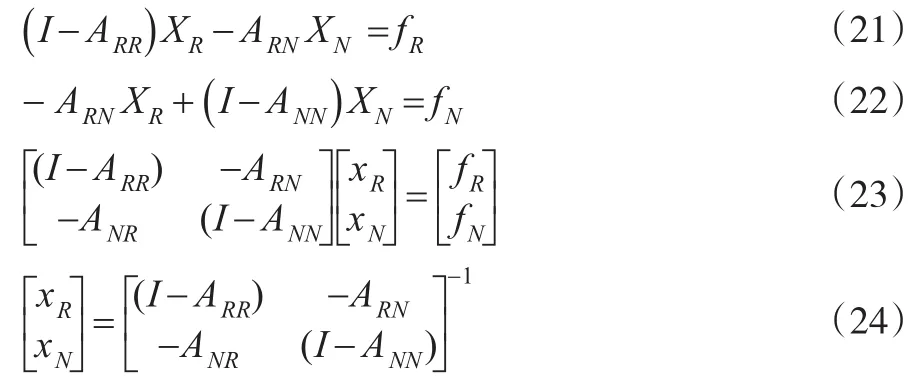
每个地区按照一个事先规定的市场份额τN提供全国性部门产品,这样通过市场份额矩阵的引入,全国性部门的产出就分配到了各个地区。以r地区为例,其市场份额为:

表示r地区提供的全国性产品的数量,xN为全国性部门商品总量。根据式(25),有:

而r地区的地区性产品产量,可由如下投入产出式表达:
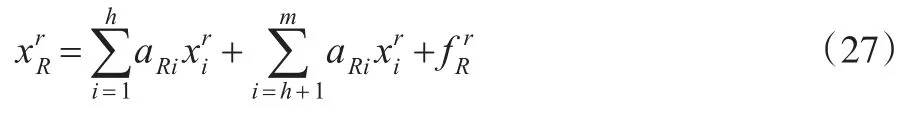
用矩阵形式表示为:
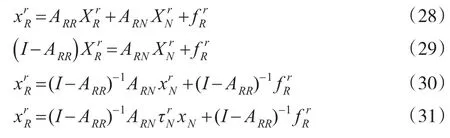
结合式(24),由外部因素导致的全国性商品或地区性商品最终需求的变化对地区产出的影响就可以测算出来,这也是Leontief模型要实现的最主要目的。
1.4.2对Leontief模型的评价
Leontief模型的运行需要三方面的数据:国家投入产出表、全国性产品由地区生产的比例因子和地区的最终需求。相对而言,该模型数据需求量较小,且容易获取,具有一定的可操作性。但它比较简单、粗糙,这主要表现在:(1)该模型对全国性与地区性两大部门的划分是较为随意的,甚至是根据“直觉”来判定;(2)假定了直接消耗系数与全国投入产出表一致。此外,该模型在计算过程中,容易低估地区间的反馈效应。
1.5Leontief-Strout模型
Leontief-Strout模型提出的时间是1963年,也称作Pool-Approach模型,或地区间引力模型、重力模型。其核心思想是:对某一地区的消费者来说,它所消费的货物来自何处并不重要,可以看作是从其所在地区的需求池订货和取货,同时假设每个地区内某一种货物或者服务的生产者把他们的产出统统汇集在一个地区供给池内。因此,在一个多地区经济中,某种个别货物或服务的所有地区间流动可以看作是该种货物的地区供给池向地区需求池供货。
1.5.1Leontief-Strout模型的基本框架
该模型由三部分组成:


式(33)表示P地区运送给所有地区第i种产品的数量之和等于p地区产量。

式(34)表示所有地区运给q地区的第i种产品的数量之和等于q地区的总使用量。将两者相加:
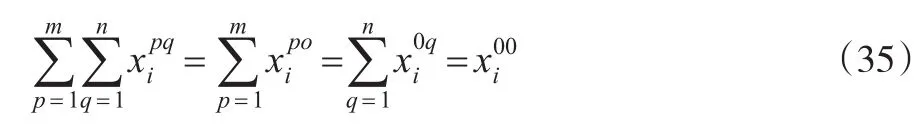

该方程表示,p地区供应q地区第i种产品的数量,与p地区第i种产品的产量大小成正比,与供应q地区的第i种产品数量成正比,与i产品的全国总产量大小成反比。而Qpq是两区域之间的摩擦系数,该系数可采用一些辅助参数方法确定。
1.5.2对Leontief-Strout模型的评价
Leontief-Strout模型中的引力方程是估算区域间贸易流量的重要方法,它只需要一些较易获取的总量数据及其他可用统计学方法估计的辅助参数就可确定。不过Leontief本人仅对该模型进行了测试,并没有展开实证分析。以该模型为理论框架的一些实证研究发现,它并不适用于规模较大的数据。
2 模型比较
2.1对Isard模型与Chenery-Moses模型的比较
在五种模型中,影响力最大的是Isard模型与Chenery-Moses模型,有关两者关系的探讨也最引人关注。
在一篇综述性文献中,李晓、张建平[9]对这两个模型进行了对比,认为他们的共同点主要表现在三个方面:(1)都是基于产业产出方向(投入产出表的行向)的均衡方程推导出的;(2)都假定了直接投入系数的稳定性,并给予了合理解释;(3)关于线性、规模报酬不变性、产业间不相关性的基础假设是保证模型有正解的条件。实际上,经过一定的变换,Isard模型能够非常容易的转化为Chenery-Moses模型。
关于两个模型的不同之处,理论界的观点基本一致[10,11]。首先在建模出发点上,Isard模型从消费地出发进行考虑,把一个地区对某种产品向各个地区(包括本地区)供应的百分比,即行系数固定下来,而Chenery-Moses模型则从生产地出发进行考虑,把一个地区对某种产品的需求量由各个地区(包括本地区)供应的百分比,即列系数固定下来。建模出发点的不同导致了矩阵形式的差异。其次,与Isard模型相比,Chenery-Moses模型所需要的数据量显然更少,构建同样有m个区域、n个部门、z类最终需求的模型,Chenery-Moses模型的数据需求比Isard模型少n×(z×m-m-z)个。
数据需求量的差异导致两个模型在应用范围上的明显区别。Isard这一“理想的”模型应用范围极窄,而Chenery-Moses模型是目前最流行的地区间投入产出建模框架。
2.2其他各模型之间的比较
Leontief模型包含了地区模型的基本形式,与其他模型相比,它衡量的仍然是“空间效应”(spatial effect),而不是“区际空间效应”(inter-spatial effect),另外,它只关注国家部门产品需求变化对地区产出的影响,并没有考虑到地区间的溢出与反馈效应[12]。
Chenery-Moses模型、行系数模型、Riefler-Tiebout模型、Leontief-Strout模型等都是对“理想的”Isard模型的实证应用,它们通过一定的假设,在降低部分Isard模型精度基础上,简化了数据处理过程。贸易系数具有稳定性是这些模型的共同点。另外,这几种模型都是从每个地区的产品生产是为了满足所有地区的需求这一角度着手的,因此存在形式上的相似之处,但都没有深入到部门对部门的层次[12]。
它们的主要区别在于贸易系数的计算方法不同:Chenery-Moses模型在列和基础上计算贸易系数,行系数模型在行和基础上测算贸易系数,而Leontief-Strout模型中的贸易系数是区域商品总流入、总流出及区域之间运输成本的函数。
Richardson将Chenery-Moses模型与行系数模型、Leontief-Strout模型进行了对比,认为行系数模型从供给角度建模,没有考虑任何区域的需求水平,与现实情况不符,也违背了Walrasian的投入—产出假定[13]。Leontief-Strout模型内含了行系数模型的一些特征,也存在相同的问题。其次,在求解地区间贸易矩阵时,Leontief-Strout模型中的摩擦系数矩阵可能无法计算出,而Chenery-Moses模型能够利用一些替代数据求解,所需数据量相对更小,计算精度也令人满意。
上述对比主要是从理论层面进行的,还有一些研究利用真实的区域间贸易流量数据对这些模型的精确程度进行了实证检验。在各种模型的综合对比中,Chenery-Moses模型在理论的完备性、估计结果的精确性、现实的可操作性等层面都具有一定优势,也逐渐成为许多国家构建地区间投入产出模型的基础框架。
2.3五种模型的综合比较
Batten[14]将五种“古典型”模型与基于统计推断与信息理论方法的现代方法相区别,认为五种古典模型建立在两种理论基础之上:一是按产地划分的需求理论,Isard模型、Chenery-Moses模型与Riefler-Tiebout模型即是如此;二是贸易库(trade pool)理论,对应的是Leontief模型、Leontief-Strout模型。更重要的是,这五个古典模型可以根据其假定的区域间贸易系数结构进行分类与对比,通过区域间贸易系数的性质进行等级分类,如表2所示。

表2 古典区际间投入—产出模型的层级结构
根据这一分类方法,五种古典模型按照可一般化的程度和可操作性顺序排列,依次为Leontief模型、Leontief-Strout模型、Chenery-Moses模型、Riefler-Tiebout模型、Isard模型。
3 结论与讨论
地区间投入产出模型作为跨区域经济、环境政策分析的重要工具,对深入了解区域之间的互动关系、统筹区域协调发展具有重要意义。受制于数据获取困难、工作量巨大等因素,国内外构建的地区间投入产出模型数量远远少于理论探讨性文章的数量,但随着大量资源、环境及产业关联等跨区域问题的出现,地区间投入产出模型的作用重新受到重视。本文阐述了Isard模型、Chenery-Moses模型、Riefler—Tiebout模型、Leontief模型、Leontief—Strout模型五种“古典型”地区间投入产出模型的基本框架、优劣势和适用性,从假设前提、可操作性等方面对各模型进行了较为系统的比较分析。通过分析发现:五种模型都有较为完善的理论框架和适用范围,其中Chenery-Moses模型所需信息量较小、精确度也较高,因此,在原始数据较为缺乏的条件下,可首先考虑应用该模型编制地区间投入产出表。
在区际联系日益加强的宏观背景下,地区间投入产出模型构建具有现实的迫切性,更多的研究力量,尤其是团队力量,应该加入到对地区间投入产出模型的研制与分析中来。在未来,本文认为以下三个方面的研究内容值得重视:一是继续研究区域间贸易流量估算方法,进一步验证各种方法的精确性,以寻求最合适的方法;二是在多种范围层次上构建模型,解决各种尺度跨区域的经济、环境问题;三是将投入产出方法与其他计量方法相结合,以扩大该方法的应用领域。
[1]陈锡康,杨翠红.投入产出技术[M].北京:科学出版社,2011.
[2]张阿玲,李继峰.地区间投入产出模型分析[J].系统工程学报,2004, (19).
[3]Isard W.Interregional and Regional Input-Output Analysis:A Model of a Space-Economy[J].The Review of Economics and Statistics,1951,33 (4).
[4]Chenery H.Regional Analysis[A].Chenery H,Clark P B(eds).The Structure and Growth of the Italian Economy[C].US:Mutual Security Agency,1953.
[5]Moses L N.The Stability of Interregional Trading Patterns and In⁃put-Output Analysis[J].The American Economic Review,1955,45(5).
[6]Riefler R,Tiebout C.Interregional Input-Output:An Empirical Califor⁃nia-Washington Model[J].Journal of Regional Science,1970,10(2).
[7]Leontief W.InterregionalTheory[A].Leontief W.StudiesintheStructure of the American Economy[C].New York:Oxford University Press,1953.
[8]Leontief W,Strout A.Multiregional Input-Output Analysis[A].Barna T.Structural Interdependence and Economic Development[C].Lon⁃don:St.Martins Press,1963.
[9]李晓,张建平.东亚产业关联的研究方法与现状——一个国际/国家间投入产出模型的综述[J].经济研究,2010,(4).
[10]Hartwick J M.Notes on the Isard and Chenery-Moses Interregional Input-Output Models[J].Journal of Regional Science,1971,11(1).
[11]Leontief W,Morgan A,Polenske K,et al.The Economic Impact-In⁃dustrial and Regional of an Arms Cut[J].The Review of Economics and Statistics,1965,47(3).
[12]Miller R E,Blair P D.Input-Output Analysis[M].London:Cam⁃bridge University Press,1985.
[13]Richardson H W.Input-Output and Regional Economics[M].Lon⁃don:Weidenfeld and Nicolson,1972.
[14]Batten D,Martellato D.Classical Versus Modern Approaches to In⁃terregional Input-Output Analysis[J].The Annals of Regional Sci⁃ence,1985,19(3).
(责任编辑/易永生)
F223
A
1002-6487(2016)22-0021-06
国家“十二五”科技支撑计划项目(2011BAJ07B07);山西省高等学校哲学社会科学研究项目(115544901002)
丛建辉(1987—),男,山东潍坊人,博士,讲师,研究方向:资源经济与管理。刘庆燕(1992—),女,山东平遥人,硕士,研究方向:产业经济与低碳经济。李文举(1993—),男,山西朔州人,硕士,研究方向:产业经济与低碳经济。
