非线性半参数空间变系数模型的两步估计

曹连英,张　博

(东北林业大学 理学院，哈尔滨 150040)

非线性半参数空间变系数模型的两步估计

曹连英,张博

(东北林业大学 理学院，哈尔滨 150040)

文章对非线性函数与空间变系数模型组合的半参数模型进行研究，提出该类模型的两步估计，给出半参数模型中非线性函数和空间变系数参数估计的精确表达式。并进行了数值模拟，结果表明，估计值与真实值拟合程度较好，方法的精确度较高。

半参数模型；地理加权回归；两步估计法

0　引言

半参数模型自1986年提出以来，由于此模型兼具参数模型和非参数模型的优点，在过去的三十年里受到统计学家和计量学家们的广泛研究，并应用于生物、农业、GPS定位等许多实际问题中。近年，赵坷[1]提出一种新型加权半参数模型，通过比较参数和半参数部分所占的比重，对其进行加权，验证了加权半参数模型的优越性；朱晋伟等人[2]根据半参数模型能减小误差，也能减少“维数灾难”的特点，将其应用到企业间创新绩效的影响因素的分析中。

目前学者研究的半参数模型主要以线性模型和变系数模型的组合为研究热点。Zeger等人[3]曾用迭代法对非参数部分进行估计，用后移算法估计线性部分，并将该半参数模型应用到实际医学领域；Caroll和Lin[4]等人利用广义估计方程研究了以线性模型为分量的半参数模型。He等人[5]在估计半参数模型时，对线性部分采用M-估计法，对非参数部分采用回归样条方法；封维波等人[6]在均方误差准则下对此类半参数模型中的参数的两步估计和最小二乘估计进行了比较,给出了参数的两步估计优于最小二乘估计的充分条件。

然而，在一些实际问题中会遇到这样的问题，部分变量对因变量的影响具有空间差异性，而其他变量对因变量的影响无空间差异性，但是是非线性的。本文将对以往研究的半参数模型中线性部分推广为非线性函数，对由一个自变量的非线性函数与空间变系数模型组合的半参数模型其估计方法进行探讨。

1　非线性半参数空间变系数模型

设非线性半参变系数模型为：

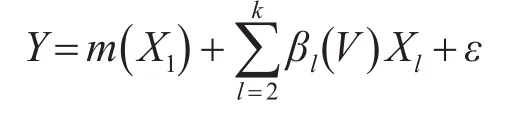
其中，Y为因变量，X1，X2，…，Xk为自变量，V为空间变量V=(u，v)。 m(X1)为未知的非线性函数，βl(V)为空间变系数模型部分的系数参数函数。ε为误差项，满足且m(X1)为足够光滑的函数，有任意阶导数。

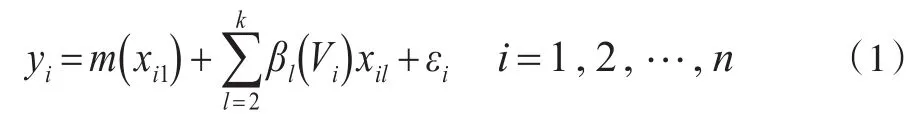
2　非线性半参数空间变系数模型的估计

由Taylor公式，m(x)在x=x0点处泰勒展开式为：

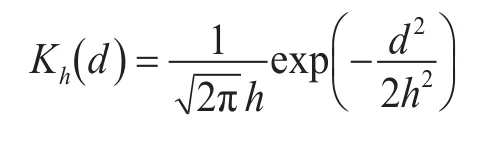
若记：

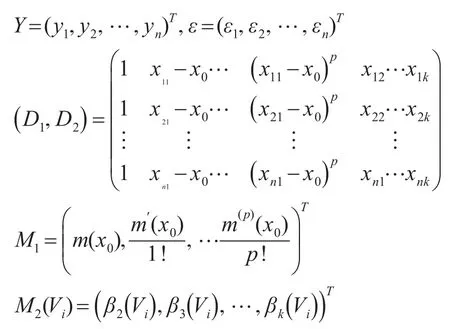
此时式（1）为：

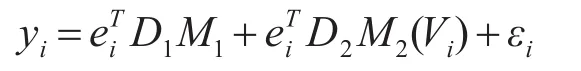
非线性半参变系数模型的估计问题转化成M1，M2(V)的估计。这里为第i个单位坐标向量。

首先假设m(x)已知，即M1已知，则模型（2）可以表示为：

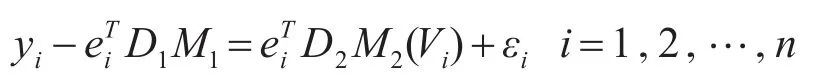
利用空间地理加权回归方法得空间变系数模型部分变系数M2(V)在点Vi=(ui，vi)的估计表达式为：

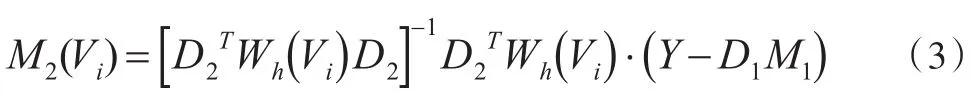
再将上式代入到式（2）：

式(4)可整理为只含有未知参数系数M1的线性回归问题如下：

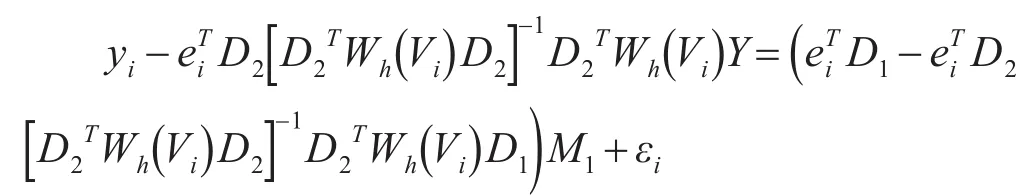
利用最小二乘估计可得上式中M1的估计为：

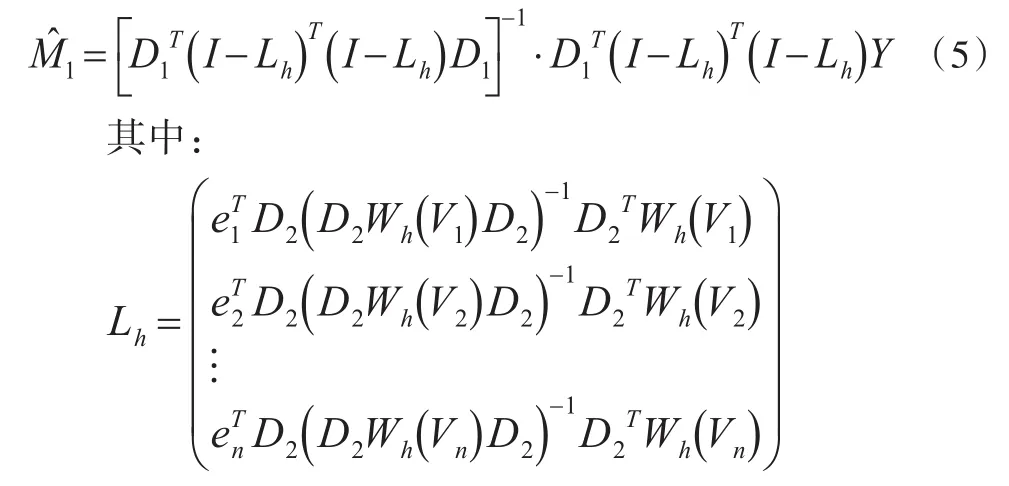
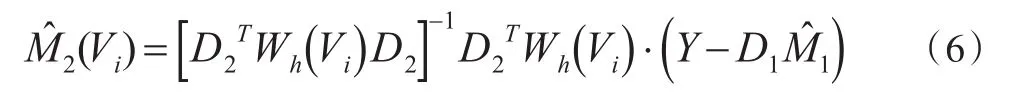
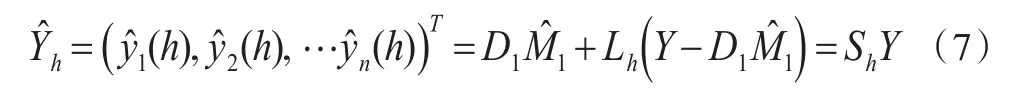
其中：

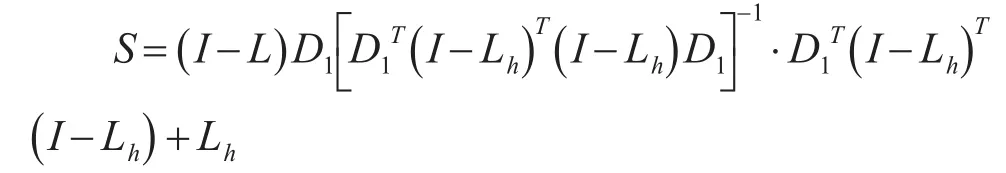
3　模拟试验

下面将通过一系列的模拟试验来考察上文提出的非线性半参数变系数模型中的线性函数和空间变系数参数估计的精确性。

模拟实验的空间区域边长为m-1个单位的正方形，以此区域的左下角为坐标原点，将正方形的边长m-1等分，等分后得到m×m个格子点。这样的格子点分隔方法有着广泛的应用背景,例如在地理分析中遥感数据的空间位置常用述格子点形式。若分别以u，v表示格子点的横纵坐标，则Vi=() ui，vi为第i个自变量与因变量的地理位置，其中表示i-1除以m的余数，表示商的整数部分，i=1，2，…，n，n=m2。模型中其他自变量的取值是独立产生的服从区间[0，1]上均匀分布的随即数。如若不然可将实际问题变量数值标准化。取x0=0.5。

就三组非线性半参数空间变系数模型进行数值试验：

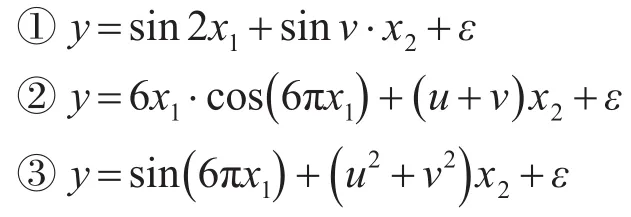
误差项ε服从正态分布N(0，σ2)，分别取标准差为σ=1，0.6，0.2，m=10，9，8进行模拟试验。对于每个σ，m只改变随机误差ε重复运算300次，获取试验结果。记非线性函数m(x)的均方误差为MSE1,变系数部分的均方误差MSE2和因变量估值的均方误差MSE3：

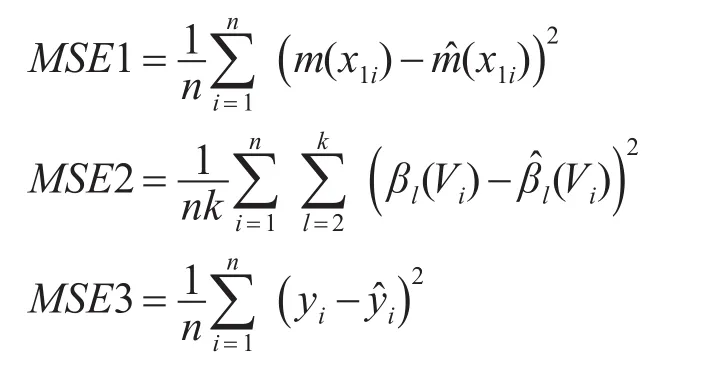
三组模型300次实验结果如表1所示，非线性函数的估值曲线与真实曲线见下页图1至图3。

数值结果表明，在不同的σ、m下，半参数模型的估计值与真实值非常接近，拟合效果较好。随着σ变小，即噪声方差变小，对模型的干扰减弱，估计的精度明显提高。m越大，即随着观测点的增多,对于以上模型来说估计值逼近精确值的程度影响不大。

表1　三组模型300次实验下的均方误差

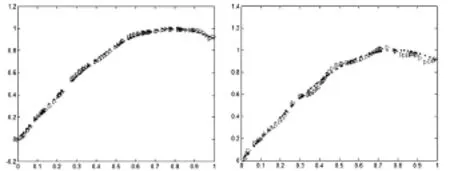
图1　回归模型（i）中非线性部分sin2x1图像和在方差分别为0.2, 1方差下的拟合图（*为真值，△为拟合值）

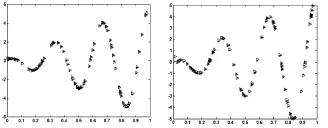
图2　回归模型（ii）中非线性部分6x1·cos(6　πx1)图像和在方差分别为0.2,1方差下的拟合图（*为真值，△为拟合值）

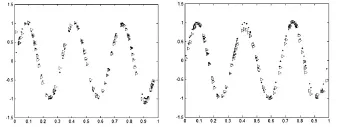
图3　回归模型（iii）中非线性部分sin(6　πx1)图像和在方差分别为0.2,1方差下的拟合图（*为真值，△为拟合值）

4　结论

本文用两步估计法对非线性半参数空间变系数模型进行估计，并给出估计表达式，模拟试验表明，估计值与真实值拟合程度较好，方法的精确度较高。在本文估计中使用了泰勒展开式，为提高计算的精度，建议解决实际问题时对变量先进性数据标准化。

[1]赵坷,付政庆,刘国林.加权半参数模型及其应用效果分析[J].大地测量与地球动力学,2014,34(2).

[2]朱晋伟,梅静娴.不同规模企业间创新绩效影响因素比较研究[J].科学与科学技术管理,2015,36(2).

[3]Zeger S L.Semiparametric Models for Longitudinal Data With Appli⁃cation to CD4 Cell Numbers in HIV Seroconverters[J].Biometrics, 1994,50(3).

[4]Lin X,Carroll R.J.Semiparametric Regression for Clustered Data Using Generalized Estimating Equations[J],Journal of the American statistical Association,2001,96(9).

[5]He X,Zhu Z,Fang W.Estimation in a Semiparametric Model for LongitudinalDataWithUnspecifiedDependenceStructure[J]. Biometrika, 2002,89(3).

[6]封维波,刘琼荪.半参数模型中两步估计与最小二乘估计的比较[J].统计与决策,2008,(4).

（责任编辑/易永生）

O212.7

A

1002-6487（2016）22-0012-03

国家自然科学基金资助项目（31270596）

曹连英（1976—），女，黑龙江人，博士，副教授，研究方向：参数统计及数学模型。