基于DSM-CSI的非线性逆散射算法研究

莫仲念，周辉林，段荣行，王玉皞

(南昌大学信息工程学院电子信息工程系，江西南昌 330031)



基于DSM-CSI的非线性逆散射算法研究

莫仲念，周辉林，段荣行，王玉皞

(南昌大学信息工程学院电子信息工程系，江西南昌 330031)

由于反演问题中散射体所处区域和散射体个数信息的缺失，进而导致非线性逆散射方法的待重构空间维数高和运算代价高.基于线性逆散射方法在重构目标区域和目标个数信息的计算代价低，本文提出一种DSM(Direct Sampling Method)线性方法和CSI(Contrast Source Inversion)非线性方法相结合的非线性逆散射方法.该方法利用DSM方法的重构结果为CSI方法提供散射体所处区域和散射体个数的先验信息，进而降低待重构空间的维数以及非线性逆散射问题的计算量.实验计算结果证明了该方法的有效性.

逆散射；直接抽样方法；对比源反演

1 引言

电磁场逆散射方法是利用测量散射场数据和电磁场前向模型，重构目标的几何形状或电性能参数，近年来已经广泛应用于目标识别、生物医学成像、遥感、地球物理成像、无损测试和评价等领域[1～3].大多数电磁场逆散射算法在某种形式上都依赖于散射体内外场的Lippmann-Schwinger方程或者域积分方程[4].由于这两个方程所具有的非线性和病态性，使其求解和计算过程极具挑战.

针对非线性问题导致计算复杂度高的问题，近年来提出一种基于玻恩近似[5,6]的线性化方法，该方法假设散射体为弱散射体，其隐含两个条件：(1)目标与背景介质的对比度小；(2)目标尺寸小于波长.在该假定条件下，目标区域的总场近似等于入射场.在此基础上运用TSVD和Tikhonov等正则化方法求解该线性病态方程.但线性电磁场逆散射成像方法只能定性实现散射体目标的检测定位和粗略地估计其几何形状，不能定量重构散射体的电性能参数.而在某些应用场景中除了需重构目标几何形状外，还需重构目标的电性能参数[7].

实际应用中绝大多数散射体属于强散射体，使得线性算法的假设不成立.随着计算机性能和存储性能的不断提升，近年来非线性逆散射算法成为研究的热点.其求解思路将逆散射问题转化为优化问题，通过构建目标函数和迭代优化方法实现目标的几何形状和电性能参数非线性重构.非线性算法则有对比源反演(Contrast Source Inversion,CSI)[8]、子空间优化方法(Subspace Optimization Method,SOM)[9]、玻恩迭代法(Born Iterative Method,BIM)[10]及其变形(Distorted Born Iterative Method,DBIM)[11]等.非线性逆散射算法需已知目标所处区域和目标个数的先验信息，但该先验信息通常是未知的，且重构结果极大地受初始值的影响[7].有鉴于此，本文提出一种DSM[12]线性算法和CSI非线性算法相结合的混合成像方法.该方法利用DSM的快速运算优势，实现快速目标定性成像，重构结果为CSI方法提供目标个数及所处区域的先验信息，并将其作为CSI方法的初始假设，从而克服传统CSI方法对先验信息的要求，及降低待重构空间的维数，最终降低非线性逆散射问题的复杂度和提升优化迭代速度.

2 电磁场非线性方程

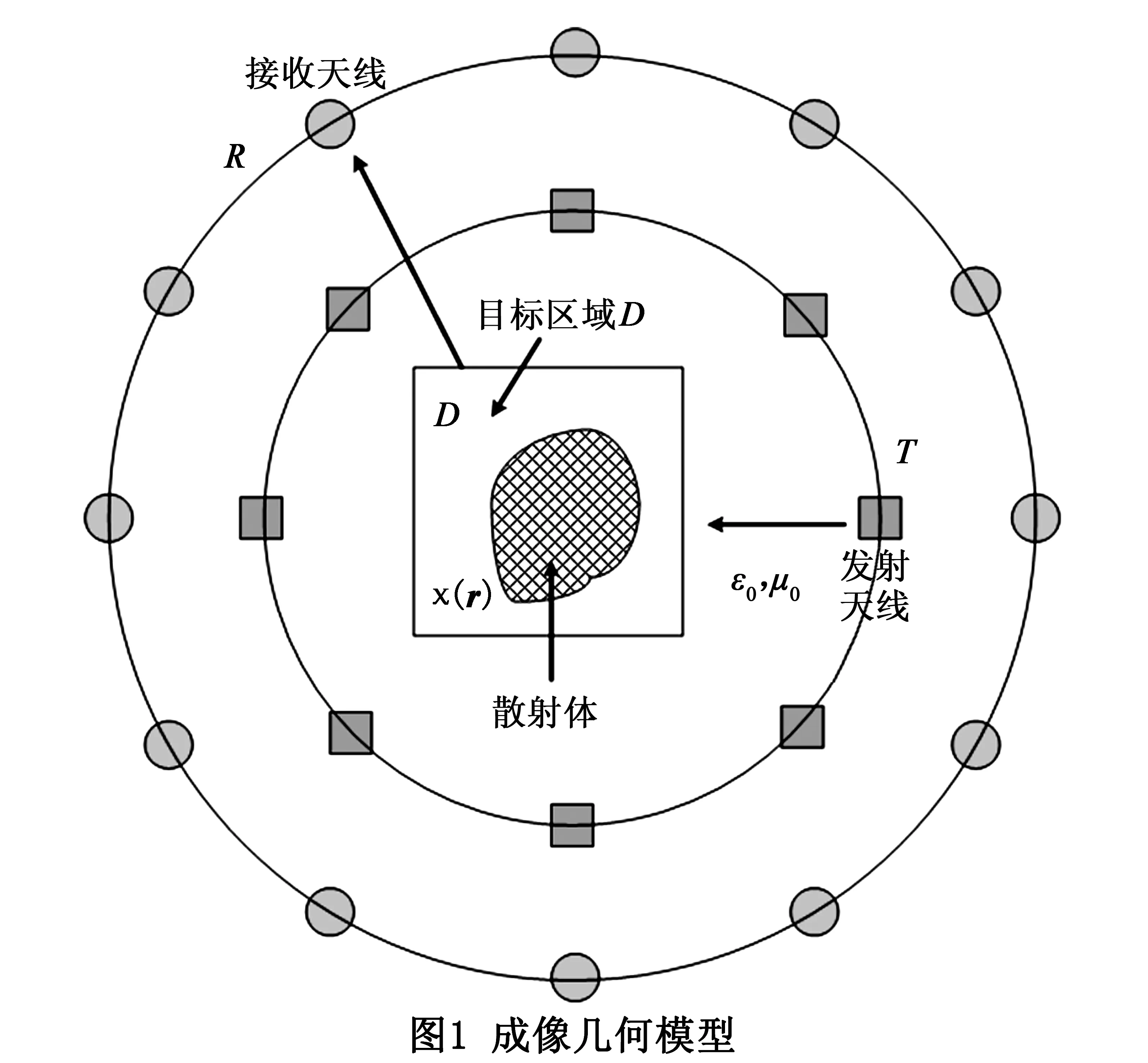
考虑一个二维成像几何模型如图1所示，假定背景介质均匀无界，其中存在一个有界的非均匀目标区域D，区域D中包含一个或多个散射目标，散射目标的位置和对比度函数χ(r)未知.在TM极化条件下，同一频率发射天线和接收天线分别按圆形轨迹T和R等间隔分布，其位置矢量分别为rj(j=1,2,…,Nj)和rq(q=1,2,…,NS).在目标区域D内的总场满足积分方程

r∈D

(1)

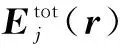
(2)

其中ε(r′)和σ(r′)分别为散射目标的介电常数和导电率.

在接收天线处接收到的散射场满足积分方程

(3)

将目标区域D划分为M个面积相等的方形网格，网格中心的位置矢量为rm(m=1,2,…,M)，每个网格面积用ΔS表示.则积分方程(1)和(3)可用离散形式表示

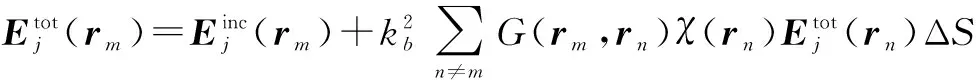
m=1,2,…,M

(4)

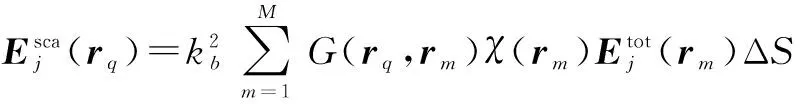
rq=1,2,…，NS

(5)

将方程(4)用矩阵形式表示

同理将方程(5)写成矩阵形式

(7)

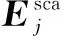
3 基于DSM-CSI的混合成像方法

基于线性算法的快速成像结果能够满足非线性算法对目标区域和目标个数先验信息的要求，本章将提出一种线性和非线性算法相结合的混合非线性成像算法.此算法能够降低非线性算法求解逆散射问题中未知网格信息个数，减少计算复杂度和降低计算代价.

3.1 DSM方法

本文采用一种DSM线性算法直接估计散射体目标形状和位置，相比MUSIC(Multiple Signal Classification)[13,14]和LSM(Linear Sampling Method)[15]线性电磁场逆散射成像算法，该算法并不涉及任何的矩阵运算，所以DSM算法运算代价低.在DSM算法中，在第m个目标网格处定义一个定性评价函数

(8)

式中，||·||表示取L2范数，〈·〉表示取内积，假如Φj(m)≈1，则此网格在散射体内；相反若Φj(m)≈0，此网格在散射体外.

3.2 CSI反演方法

(9)

同理方程(7)写为

(10)

目标函数的构建是逆散射算法的重要组成部分，定义目标函数为

(11)

上式右端第一项为归一化的场数据方程误差，第二项为归一化的场状态方程误差.该目标函数是关于ωj的二次函数，但关于χ的非线性函数.实际应用表明，CSI算法是最有效的非线性逆散射算法之一.

3.3 DSM-CSI方法

本文结合以上两种方法提出一种DSM-CSI方法，该方法利用DSM的重构结果为CSI方法提供散射目标个数及其所处区域信息，进而减少待重构空间χ维数，从而降低整个非线性算法的计算量.具体结合DSM-CSI算法流程如算法1所示.

算法1 DSM-CSI算法流程

1.利用DSM方法为CSI方法提供散射体先验信息

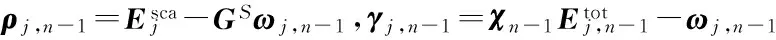
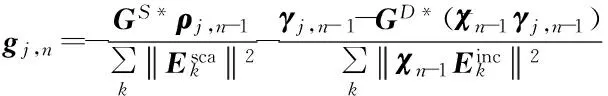
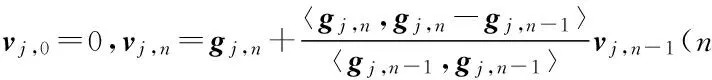
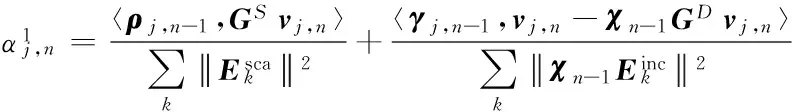
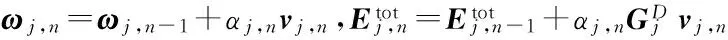
10.当式(11)小于某个设定值时则终止迭代输出χn，否则n=n+1，返回4.

4 实验结果分析

在本实验中散射体对比度实部即相对介电常数大致范围已知，可由相对介电常数误差来衡量反演重构算法误差.定义相对介电常数误差

(12)

式中χmax为反演重构对比度中最大值，χr为散射体真实介电常数最大值.当相对介电常数误差小于终止条件时，反演迭代终止.

在本节中，分别运用DSM、CSI和DSM-CSI方法对散射体逆散射反演成像，并对重构结果进行对比分析.本实验中散射体的导电率未知，为验证算法的成像效果，本文中CSI和DSM-CSI算法的成像结果只给出相对介电常数分布图并与散射体目标的真实相对介电常数对比.

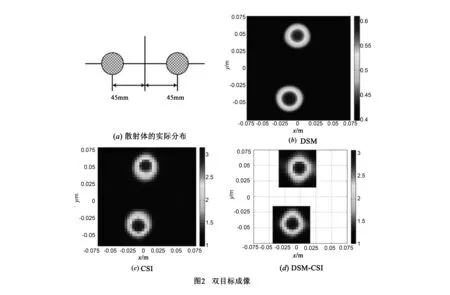
利用来自菲涅尔实验室的数据(twodiel-TM 8f.exp)[16]重构散射体.图2(a)为实验中散射体横截面，图中描述了散射体的实际个数、位置和形状大小，两个圆柱形散射体分别位于原点的两侧，半径为15mm，圆心到原点距离为45mm，背景介质为自由空间，散射体的相对介电常数在3±0.3之间.36根发射天线均匀分布于圆心在实验装置中心的圆上，半径为0.72m,49根接收天线分布于半径为0.76m的圆上，在反演中选取频率f=4GHz的数据重构散射体参数.

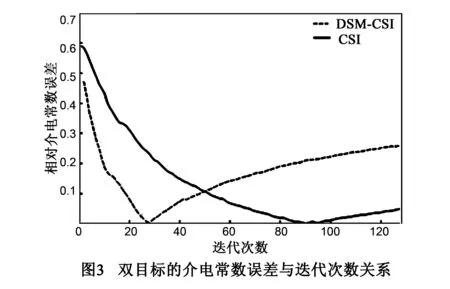
选取0.15m×0.15m的目标区域，将其划分为120×120个网格，每个网格的大小等于1.25mm×1.25mm，DSM方法重构结果如图2(b)所示，从图中可以确定散射目标所处区域和目标个数并跟实际场景相符，但DSM方法并不能重构散射体的对比度.利用CSI算法，将目标区域剖分为40×40个网格，成像结果如图2(c)所示，所重构相对介电常数值跟实际介电常数值非常相近.运用DSM-CSI方法，根据图2(b)的成像结果，可将目标区域缩小为两个0.06m×0.06m的目标区域，为保持与CSI方法网格尺寸相同，将每个目标区域剖分为16×16个网格，反演结果如图2(d)所示，散射体相对介电常数反演值也非常接近实际值.对比图2(c)和图2(d)，CSI算法和DSM-CSI算法的反演质量相差不大.DSM-CSI方法和CSI方法的相对介电常数误差与迭代次数如图3所示，根据终止条件式(12)，可知DSM-CSI迭代次数比CSI迭代次数少得多.通过对比分析，运用CSI方法需要重构出40×40个网格信息，而DSM-CSI方法仅仅需要重构16×32个网格信息，有效的减少了逆散射问题的未知量个数.DSM-CSI的核心算法是CSI算法，由于DSM-CSI方法减少了待重构空间的维数，所以DSM-CSI方法的每次迭代时间比CSI方法少得多，因此DSM-CSI方法总的运算时间大大少于CSI方法.

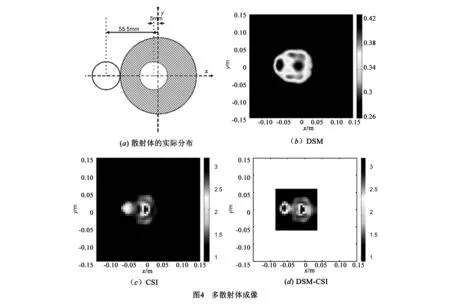
采用来自菲涅尔实验数据(FoamTwinDielTM)[17]，运用三种不同的反演方法逆散射成像得出的结果如图4所示.实验中散射体的横截面如图4(a)所示，一个半径为15.5mm的圆柱体包含于一个半径为40mm的圆柱体内，而一个半径同样为15.5mm的圆柱体与大圆柱体相切.大圆柱体和小圆柱体的相对介电常数分别为1.45±0.15和3±0.3.在实验中，18根发射天线均匀分布于圆心在实验装置中心的圆上，半径为1.67m，241根接收天线分布于半径为1.67m的圆上用于接收散射场数据，利用频率f=5GHz的实验室数据重构反射体目标形状、位置或对比度分布.

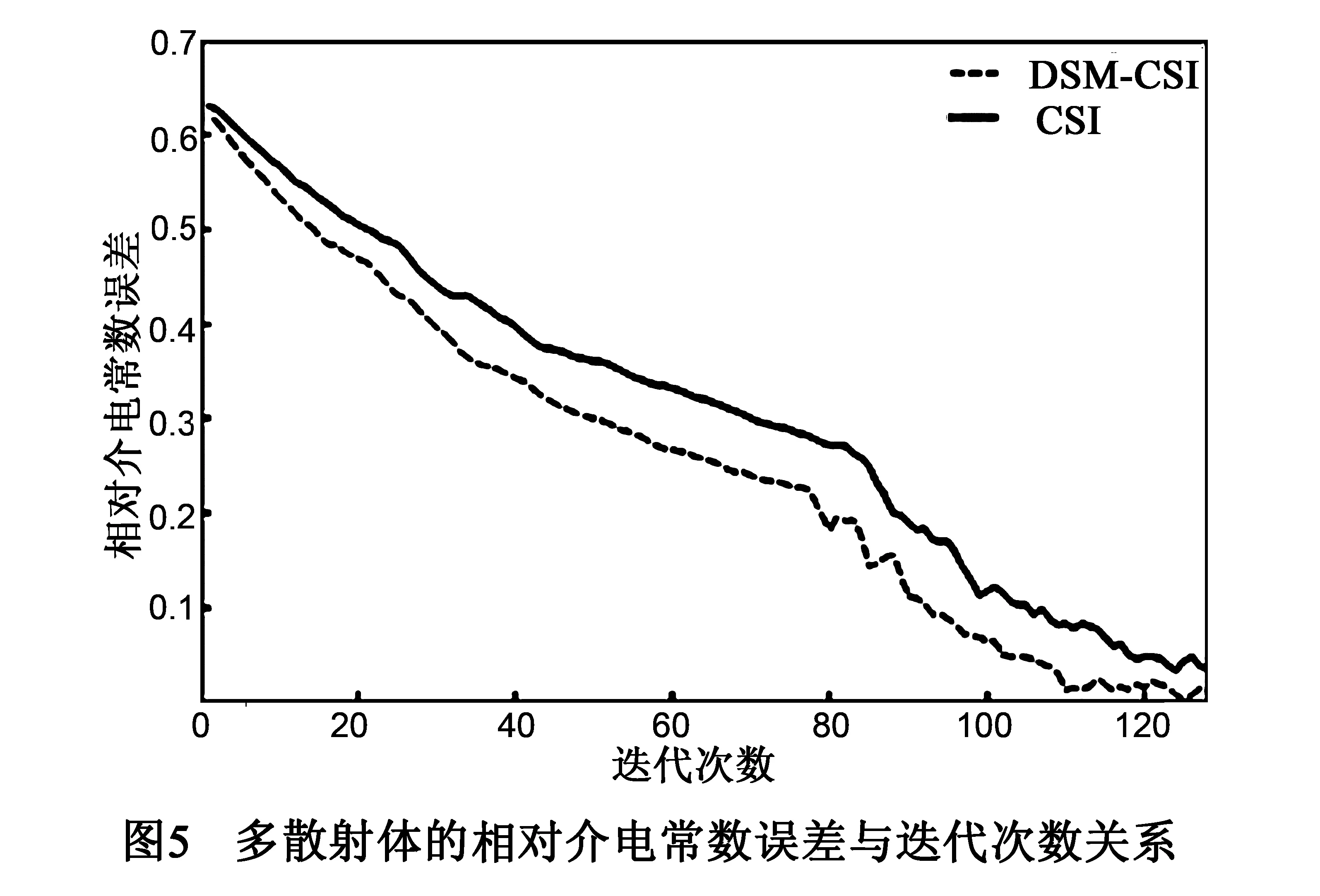
假定已知散射体位于0.3m×0.3m的目标区域内，实际位置以及形状未知.运用DSM算法，成像结果如图4(b)所示，可以看出DSM方法虽不能成功重构散射体的形状，但能精确重构散射体所处区域.将0.3m×0.3m的目标区域划分为50×50个网格，每个网格为6mm×6mm，利用CSI方法成像如图4(c)所示，可以看出三个散射体的位置及形状大小，且成功反演三个散射体目标的相对介电常数.根据图4(b)，DSM重构结果为CSI方法重新选取目标区域大小为0.12m×0.12m，将目标区域剖分为20×20个网格，网格尺寸与图4(c)相同，DSM-CSI反演成像如图4(d)所示，DSM-CSI成像效果跟CSI方法一致.DSM-CSI方法和CSI方法的相对介电常数误差与迭代次数如图5所示，从图中可知DSM-CSI方法的相对介电常数误差随着迭代次数增加而减少速度比CSI方法略快，在式(12)的终止条件下，两种算法的迭代次数相差不大.相比CSI算法，DSM-CSI算法极大减少了逆散射问题中的未知量个数，这极大降低了重构问题的运算代价，从而降低运算时间.在逆散射反演问题中运算时间是衡量一个算法优越性的重要指标，相比单一的CSI方法，DSM-CSI算法具有极大的速度优势.

5 结论

本文所提出DSM-CSI方法利用DSM为CSI方法提供先验信息，在此基础上重新选取目标区域D，然后运用CSI算法反演出散射体的相关参数.数值实验结果证明，DSM-CSI方法和CSI方法的反演质量一致，但DSM-CSI方法的计算代价大大低于CSI方法.

[1]Tuchin V V,Tuchin V.Tissue Optics:Light Scattering Methods and Instruments for Medical Diagnosis[M].Bellingham:SPIE Press,2007.

[2]Randazzo A,Estatico C.A regularisation scheme for electromagnetic inverse problems:application to crack detection in civil structures[J].Nondestructive Testing and Evaluation,2012,27(3):189-197.

[3]Colton D,Kress R.Inverse Acoustic and Electromagnetic Scattering Theory[M].Springer Science & Business Media,2012.

[4]Van Den Berg P M,Kleinman R E.A contrast source inversion method[J].Inverse Problems,1997,13(6):1607.

[5]Poli L,Oliveri G,Massa A.Microwave imaging within the first-order Born approximation by means of the contrast-field Bayesian compressive sensing[J].IEEE Transactions on Antennas and Propagation,2012,60(6):2865-2879.

[6]郑虎,李廉林,李芳.玻恩近似下的无相位检测电磁成像方法[J].电波科学学报,2008,23(4):669-673.

Zheng Hu,Li Lianlin,Li Fang.EM inverse scattering from phase less data of total field under Born approximation[J].Chinese Journal of Radio Science,2008,23(4):669-673.(in Chinese)

[7]Catapano I,Randazzo A,Slob E,et al.GPR imaging via qualitative and quantitative approaches[A].Civil Engineering Applications of Ground Penetrating Radar[M/OL].Springer International Publishing,2015.239-280.

[8]Jeffrey I,Zakaria A,LoVetri J.Microwave imaging by mixed-order discontinuous Galerkin contrast source inversion[A].General Assembly and Scientific Symposium (URSI GASS)[C].USA:IEEE,2014.1-4.

[9]Oliveri G,Zhong Y,Chen X,et al.Multiresolution subspace-based optimization method for inverse scattering problems[J].JOSA A,2011,28(10):2057-2069.

[10]赵延文,聂在平.多重网格技术与波恩迭代法相结合的反演新方法[J].电子学报,2003,31(2):171-174.

Zhao Yanwen,Nie Zaiping.A novel inversion method combining born iterative method with multi-grid technique[J].Acta Electronica Sinica,2003,31(2):171-174.(in Chinese)

[11]Ran-Duc T,Linh-Trung N,Do M N.Modified distorted born iterative method for ultrasound tomography by random sampling[A].International Symposium on Communications and Information Technologies (ISCIT)[C].USA:IEEE,2012.1065-1068.

[12]Ito K,Jin B,Zou J.A direct sampling method to an inverse medium scattering problem[J].Inverse Problems,2012,28(2):025003.

[13]樊祥,程正东,马东辉,等.两信号源的相关性对MUSIC算法分辨性能的影响[J].电子学报,2008,36(12):2315-2318.

Fan Xiang,Cheng Zhengdong,Ma Donghui,et al.Effect of correlation of two signal sources on resolution performance of MUSIC algorithm[J].Acta Electronica Sinica,2008,36(12):2315-2318.(in Chinese)

[14]郭跃,王宏远,周陬.阵元间距对MUSIC算法的影响[J].电子学报，2007，35(9):1675-1679.

Guo Yue,Wang Hongyuan,Zhou Zou.Effect of array elements spacing on MUSIC algorithm[J].Acta Electronica Sinica,2007,35(9):1675-1679.(in Chinese)

[15]Haddar H,Lechleiter A,Marmorat S.An improved time domain linear sampling method for Robin and Neumann obstacles[J].Applicable Analysis,2014,93(2):369-390.

[16]Belkebir K,Saillard M.Special section:Testing inversion algorithms against experimental data[J].Inverse Problems,2001,17(6):1565-1571.

[17]Geffrin J M,Sabouroux P,Eyraud C.Free space experimental scattering database continuation:experimental set-up and measurement precision[J].Inverse Problems,2005,21(6):S117.

莫仲念 男，1989年生，广西人，现为南昌大学在读硕士研究生，主要从事超宽带穿墙雷达成像，逆散射成像方法研究.

周辉林 男，1979年生，江西人，现为南昌大学教授、理学博士，从事超宽带雷达成像、雷达信号处理和目标识别等领域的研究.

E-mail:zhouhuilin@ncu.edu.cn

段荣行 男，1977年生，江西人，现为南昌大学副教授，主要研究方向为复杂系统可靠性分析、故障诊断及信息融合，主持和参与多项国家自然科学基金和省部级项目.

DSM-CSI Based Nonlinear Inverse Scattering Method forComplex Objects Reconstruction

MO Zhong-nian,ZHOU Hui-lin,DUAN Rong-xing,WANG Yu-hao

(DepartmentofElectronic&InformationEngineering,NanchangUniversity,Nanchang,Jiangxi330031,China)

Due to the absence of information concerning the location and number of scattering objects in inverse scattering problem,it results in nonlinear inverse scattering method calling for high refactoring space dimension and high computational cost.Based on the low computational burden with the linear inverse scattering methods in reconstructing the location and number of the targets,we propose a nonlinear inverse scattering method in this paper,which combined with DSM linear and CSI nonlinear inverse scattering methods.The reconstruction results of DSM are used as the prior information to provide the location and the number of the targets for the CSI method,which reduce the dimension of refactoring space and the amount of computation.Experimental results show the effectiveness of the proposed method.

inverse scattering problem;direct sampling method (DSM);contrast source inversion method (CSI)

2015-02-06；

2015-05-18；责任编辑：孙瑶

国家自然科学基金(No.61062009，No.71461021，No.61261010)；江西省自然科学基金(No.2015BAB207001)；江西省科技支撑计划(No.20151BBE50090)

O451

A

0372-2112 (2016)10-2501-06

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.10.031