一种基于序列和反褶序列精密初相位计算的新型正弦频率测量方法

李 军,王越超,李 锋

(广东电网有限责任公司电力科学研究院,广东广州 510080)



一种基于序列和反褶序列精密初相位计算的新型正弦频率测量方法

李 军,王越超,李 锋

(广东电网有限责任公司电力科学研究院,广东广州 510080)

正弦频率是基本的正弦参数之一,高准确度的低频正弦频率测量技术有广泛的应用.但在低频正弦频率测量方面,目前的频率测量技术在谐波噪声干扰环境下,普遍存在准确度不高的问题.文章提出了一种主要由序列和反褶序列精密初相位计算方法等构成的新型正弦频率测量方法,分析了序列精密初相位计算和将正交混频用于序列相位计算的原理,指出了混频干扰是造成正弦相位计算和正弦频率测量误差的主要内在原因.通过对混频干扰频率的深度抑制,再通过计算序列和反褶序列精密初相位得到的序列全相位差,提高了谐波噪声干扰环境下的正弦相位计算和正弦频率测量的准确度.数学计算、仿真试验和物理实验结果也验证了该方法的正确性和可靠性.

反褶序列;精密初相位;序列全相位差;正交混频器;混频干扰频率;数字滤波

1 引言

系统频率特性的分析[1～3]和系统频率的测量在本质上均是一种正弦参数的分析和测量,正弦频率测量在诸多领域有着广泛的应用[4～6],实现正弦频率测量有多种算法[6～15],文献[6]指出了一种电力系统阻抗测量方法需要有精准的正弦频率测量结果作为参考值.我国电力系统的电网运行额定工频在50Hz[16]附近,属于频率较低的正弦频率.但目前的频率测量技术在低频正弦频率测量方面普遍存在准确度不高的问题.

零交法(zero-crossing algorithm)是用于低频正弦频率测量的基本方法[6],如用于电力系统频率的测量.零交法的原理是通过1个或数个周期信号波形过零点的时间间隔来计算出此段波形的频率值.由于实际电力信号中存在谐波干扰、包括电力负荷小范围内随机波动产生的类似白噪声干扰等,因此该方法测量出的频率值存在较大的误差[6].

快速傅里叶(FFT)变换算法[7]和离散傅里叶(DFT)变换算法[8]是用于正弦参数计算的基本数学方法.其中信号的非整数周期截断引起的频谱泄漏问题是造成这些算法误差的主要原因,频谱泄漏问题客观上不可避免.

此外还有一些改进算法,如基于自适应陷波滤波器的算法[9]、基于牛顿迭代方法的算法[10]、基于小波变换算法[11]等.

文中提出将反褶序列的处理用于低频正弦频率的计算,相对现有的高准确度低频正弦频率测量方法[14,15]具有更高的准确度和可靠性.

2 新型正弦频率测量方法

新型正弦频率测量方法的基本原理是:首先通过一个频率初测单元给出参考频率,允许参考频率存在±0.25%以内的相对误差;然后根据参考频率计算正向序列和反褶序列的精密初相位;接着计算所述2个精密初相位的相位差;紧接着将所述相位差转换为正向序列的全相位差;最后将所述全相位差转换为信号正弦频率,如图1所示:

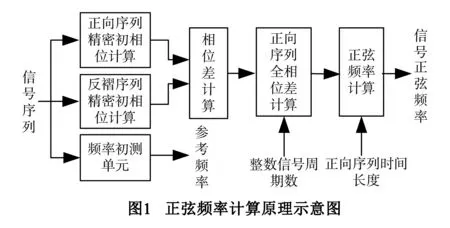
之后文中无特殊说明,信号频率均指基波频率,周期均指基波周期.

3 正向序列和反褶序列

对单基波频率的正弦信号,正向序列表达为式(1):

X(n)=Acos(ωiTn+φ)

n=0,1,2,3,…,N-1

(1)

式中,X(n)为正向序列;A为信号幅值;ωi为信号频率,单位rad/s;T为信号采样间隔,单位s;φ为正向信号序列初相位,单位rad;N为正向序列长度,单位无量纲.

之后无特殊情况,文中序列长度的单位均为无量纲,相位或相位差的单位均为rad,频率或频差的单位均为rad/s.

反褶序列,即将正向序列反向输出,表达为式(2):

XAnti(n)=X(N-n)=Acos(-ωiTn+β)

n=0,1,2,3,…,N-1

(2)

式中,XAnti(n)为反褶序列;β为反褶序列的初相位;反褶序列的频率项取负值,关系上,反褶序列初相位是正向序列的截止相位;N为反褶序列长度,等于正向序列长度.

4 序列精密初相位计算

文中采用的序列精密初相位计算方法,是基于序列和缩短序列的精密相位计算结果,如图2所示:

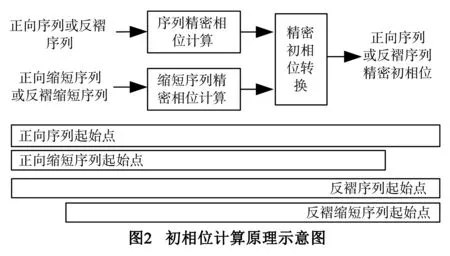
图2所示,相对正向序列和反褶序列,正向缩短序列和反褶缩短序列为式(3):

X2(n)=Acos(ωiTn+φ)

XAnti2(n)=Acos(-ωiTn+β)

n=0,1,2,3,…,NS-1

NS=N-MS

MS=(int)(0.25N2π)

(3)

式中,X2(n)为正向缩短序列;XAnti2(n)为反褶缩短序列;NS为正向或反褶缩短序列的长度;MS为相对正向序列或反褶序列长度的缩短值;N2π为信号单位周期序列长度;(int)为取整数;f为Hz单位的采样频率;ωs为参考频率;原则上MS=0.25N2π.之后文中无特殊说明,周期序列长度均指信号单位周期序列长度.

4.1 序列精密相位计算

文章采用了一种基于正交混频的序列相位计算方法,如图3所示:

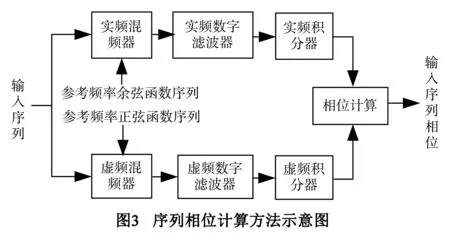
图3所示,首先对输入序列进行正交混频,然后分别对2个正交混频序列进行数字滤波,接着对2个数字滤波序列进行积分,最后根据2个积分值进行序列相位计算.

4.1.1 实频与虚频混频序列

设信号由基波、2次谐波构成为例,为式(4):

X(t)=cos(ωit+φ)+a2cos(2ωit+φ2)

(4)

所谓的混频器实际上是乘法器,在参考频率等于信号频率,简称为零混频状态,则得到输入信号的混频信号为式(5):

(5)

式中,R(t)为实频信号,I(t)为虚频信号;ωs为参考频率.其中,cos(φ)/2和-sin(φ)/2为有用成分,其余的均为混频干扰频率成分.

所述零混频状态在技术上难以实现,在参考频率不等于信号频率时,称之为非零混频状态,2个频率的频差为式(6):

Ω=ωi-ωs

(6)

式中,Ω为频差.在不考虑所述混频干扰频率成分时,得到实频和虚频混频序列为式(7):

R(n)=Acos(ωiTn+φ)cos(ωsTn)

I(n)=Acos(ωiTn+φ)sin(ωsTn)

n=1,2,3,…,N-1

(7)

式中,R(n)为实频序列;I(n)为虚频序列.

4.1.2 数字滤波

混频干扰严重影响正弦参数的计算准确度,因此设计一种针对混频干扰抑制的数字滤波,文中采用一种算术平均滤波算法,即对NT个连续离散值相加,然后取其算术平均值作为本次滤波值输出,NT也为数字滤波参数.算术平均滤波算法的主要特点是在频域上,其幅频特性曲线连续分布了等距离的陷波频率点或零增益频率点.选择合适的数字滤波参数,使陷波频率点等于混频干扰频率,可针对混频干扰频率产生完全的衰减作用.

对之后式(24)给出的信号进行零混频,得到的部分混频频率,表1所示:

表1 混频频率计算表

表1中,零频率成分为有用成分,非零频率成分均为混频干扰频率成分.在没有误差时,当NT取值为1.5N2π,能够对2ωi/3和4ωi/3混频干扰频率进行完全衰减.而NT取值为2N2π,能够对ωi/2、3ωi/2、1ωi、2ωi、3ωi、4ωi等混频干扰进行完全衰减.

综合考虑,数字滤波由2种参数的数字滤波器所构成,每种参数的数字滤波器均由参数相同的三级数字滤波组成,为式(8):

XD(n)=

X(n)，n=0,1,2,3,…,N-1

XD(n)，n=0,1,2,3,…,N-3NT1-3NT2-1

(8)

式中,X(n)为数字滤波输入序列,具体代表实频序列R(n)、虚频序列I(n);NT1为数字滤波参数1,NT2为数字滤波参数2,数字滤波参数计算隐含了整数化;XD(n)为数字滤波输出序列,具体代表实频滤波序列RD(n)、虚频滤波序列ID(n).

2级数字滤器需要使用周期序列长度的10.5倍.其中数字滤波频域幅频增益函数为式(9):

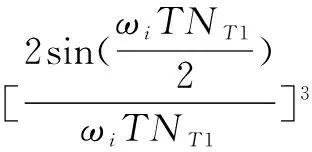
(9)

式中,K(ωi)为无量纲单位的数字滤波频域幅频增益.在采样频率10KHz,基波频率100π(对应50Hz),参考频率100π,计算得到NT1=300、NT2=400,则数字滤波频域特性如图4所示:

图4中,数字滤波频域幅频增益K(ωi)的单位为dB,在数字滤波参数没有误差时,频域滤波特性对表1给出的混频干扰频率具有完全的衰减作用.

由于参考频率存在误差,数字滤波参数存在整数化误差.其中在基波频率100π,参考频率100.25π,计算数字滤波参数NT1=299、NT2=399,则得到数字滤波对表1混频干扰频率的抑制特性,如图5所示:

图5所示,垂直线为表1给出的混频干扰频率点,给出的最小抑制度为-210dB.不考虑混频干扰频率,则实频滤波和虚频滤波序列为式(10):

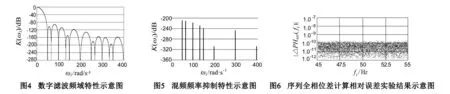
n=0,1,2,3,…,N-3NT1-3NT2-1

(10)

式中,RD(n) 为实频滤波序列;ID(n) 为虚频滤波序列;K(Ω)为数字滤波在频差Ω的增益,单位无量纲;α为数字滤波在频差Ω的移相,单位rad.

4.1.3 积分计算

实频和虚频滤波序列的积分,为式(11):

n=0,1,2,3,……,M-1

M=N-3NT1-3NT2

(11)

式中,R为实频积分值;I为虚频积分值;M为输入序列长度N在数字滤波后的剩余长度或积分长度.

4.1.4 相位计算和相位扩展

根据式(11)给出的实频积分值和虚频积分值,得到序列相位计算为式(12):

(12)

式中,PH为序列相位,范围在0～±0.5π.但实际序列相位可能会超出0～±0.5π范围,必须进行相位扩展,为式(13)

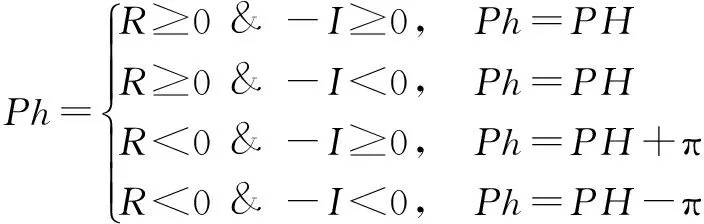
(13)

式中,Ph为扩展相位,范围0～±π;&代表与逻辑.在之后的序列相位计算隐含了式(13)给出的计算过程.

4.1.5 正向序列和正向缩短序列相位计算

根据式(11)、式(12)和式(13)等,得到正向序列相位计算式,为式(14):

(14)

式中,PhL为正向序列相位;M为正向序列长度N在数字滤波后的剩余长度或积分计算长度,原则上M=0.5N2π.

正向缩短序列相位计算为式(15):

(15)

式中,PhS为正向缩短序列相位;MS为正向缩短序列长度NS在数字滤波后的剩余长度或积分计算长度,原则上MS=0.25N2π、MS=0.5M.

4.2 正向序列精密初相位计算

将正向序列相位、正向缩短序列相位转换为正向序列初相位,为式(16):

N=3NT1+3NT2+M

NS=3NT1+3NT2+MS

(16)

式中,φ为正向序列精密初相位;N为正向序列长度;NS为正向缩短序列长度.

4.3 反褶序列精密初相位计算

进行反褶序列初相位计算的目的是为了得到正向序列的全相位差.在不考虑混频干扰频率时,得到反褶混频序列为式(17):

RAnit(n)=Acos(-ωiTn+β)cos(-ωsTn)

IAnit(n)=Acos(-ωiTn+β)sin(-ωsTn)

n=0,1,2,3,…,N-1

(17)

式中,RAnti(n)为反褶实频序列,IAnti(n)为反褶虚频序列.省略其他计算过程,得到反褶序列初相位计算为式(18):

(18)

式中,β为反褶序列精密初相位,PhAntiL为反褶序列相位,PhAntiS为反褶缩短序列相位.

5 正弦频率计算

根据正弦频率、序列全相位差、序列时间长度之间的内在关系进行正弦频率计算.

5.1 序列长度的选择

原则上要求正向序列长度对应整数信号周期数,根据参考频率计算正向序列长度,为式(19):

(19)

式中,N为正向序列长度,(int)为取整数,C2π为整数信号周期数,ωs为参考频率,T为采样间隔.正向序列长度对应整数信号周期数存在误差.

5.2 相位差计算

将正向序列精密初相位和反褶序列精密初相位转换为相位差,为式(20):

ΔPH=β-φ

(20)

式中,△PH为相位差,范围0～±2π.

5.3 正向序列全相位差计算

所谓的正向序列全相位差,也就是信号正弦频率与正向序列时间长度的乘积,表达为式(21):

ΔPh=ωiTN

(21)

式中,△Ph为正向序列全相位差;ωi为信号频率;TN为正向序列时间长度,单位s.

很显然,所述的全相位差与上述式(20)给出的相位差存在明显的区别.进一步分析可发现,式(20)给出的相位差、在数值上反映了2π整倍数的误差值.因此,根据式(20)和整数信号周期数,得到正向序列全相位差计算式,为式(22):

ΔPh=ΔPH+2πC2π

(22)

式中,△Ph为正向序列全相位差;C2π为整数信号周期数;2πC2π为2π整倍数的全相位差;当C2π=11,则2πC2π=22π,则△Ph的范围在22π左右.

5.4 正弦频率计算

信号正弦频率是正向序列全相位差与正向序列时间长度的比值,因此信号正弦频率计算,为式(23):

(23)

式中,ωi为信号正弦频率.

6 仿真实验

进行了电力系统50Hz工频正弦基波相位和频率计算仿真实验,仿真实验条件为:实验信号基波频率变化范围在45Hz～55Hz,信号的采样频率10KHz,信号的离散数据量化位数24bit,参考频率相对误差±0.25%.具体实验信号由基波,1/2、1/3、2、3、4、5次谐波成分等构成,为式(24):

(24)

在基波频率50Hz、取11整数周期信号、在参考频率50.125Hz,得到的计算结果,表2所示:

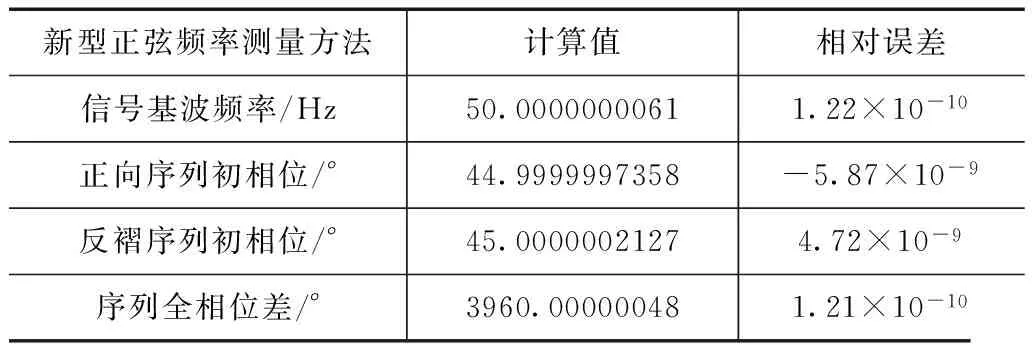
表2 新型正弦频率测量方法实验结果表

表2所示,序列全相位差的相对误差相对较小,原因是序列全相位差在数值上较大,信号基波频率相对误差与序列全相位差的相对误差基本相同.

在实验信号基波频率45Hz～55Hz范围,取11整数周期信号、参考频率相对误差取0.25%,得到序列全相位差计算相对误差随基波频率变化的实验结果,如图6所示,信号基波频率计算相对误差随基波频率变化的实验结果,如图7所示:

分析图6和图7实验结果,序列全相位差计算相对误差、基波频率计算相对误差随实验信号基波频率变化过程表现出明显的随机性,产生原因主要是离散数据量化背景噪声引起的,也表明所述混频干扰频率在数字滤波后的残余幅值已低于背景噪声水平.给出的序列全相位差计算和信号基波频率计算相对误差均在10-10量级.

此外还进行了白噪声加扰实验,通常用信噪比衡量信号的质量,表述为式(25):

n=0,1,2,3,……,N-1

(25)

式中,S:N为功率信噪比,单位dB;Es为信号序列Xs(n)在序列长度N的方差;En为白噪声序列Xn(n)在序列长度N的方差.其中在信号基波频率50Hz和取11整数周期信号,参考频率取50.125Hz,得到的实验结果,如图8所示:

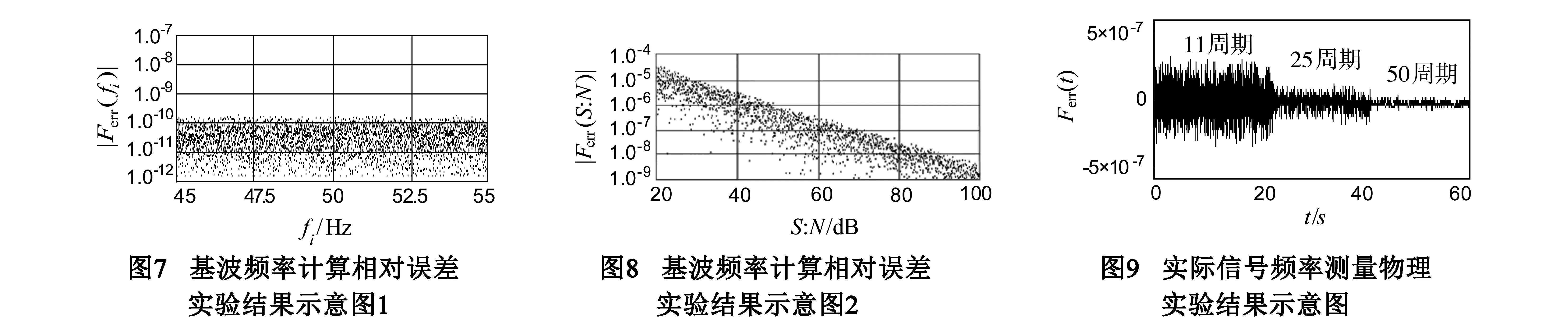
图8给出了在白噪声干扰环境下的信号基波频率计算相对误差分布图,新型正弦频率测量方法具有良好的抗白噪声干扰特性,其中在信噪比40dB时可实现10-6量级准确度的频率测量.

7 物理实验

进行了电力系统50Hz工频频率测量的物理实验,通过采集实际高准确度信号发生器或实际电力系统的信号进行相位和频率计算.具体物理实验条件为:实验频率测量系统的频率基准采用准确度±1×10-8量级的恒温晶振,采集设备的数据量化位数为24bit,采集设备的采样频率为10KHz.

在实验室环境,采集高准确度频率源信号,在45Hz～55Hz频率范围内,取11整数周期信号时得到的正弦频率计算相对误差低于|±3.1×10-7|、阿伦方差约为9.8×10-8,取50整数周期信号时的正弦频率计算相对误差低于|±8.3×10-9|、阿伦方差约为2.6×10-9,如图9所示:

另外,采集实际电力系统信号进行频率计算,同时与“零交法”频率测量方法进行对比,得到的实验结果,如图10所示:

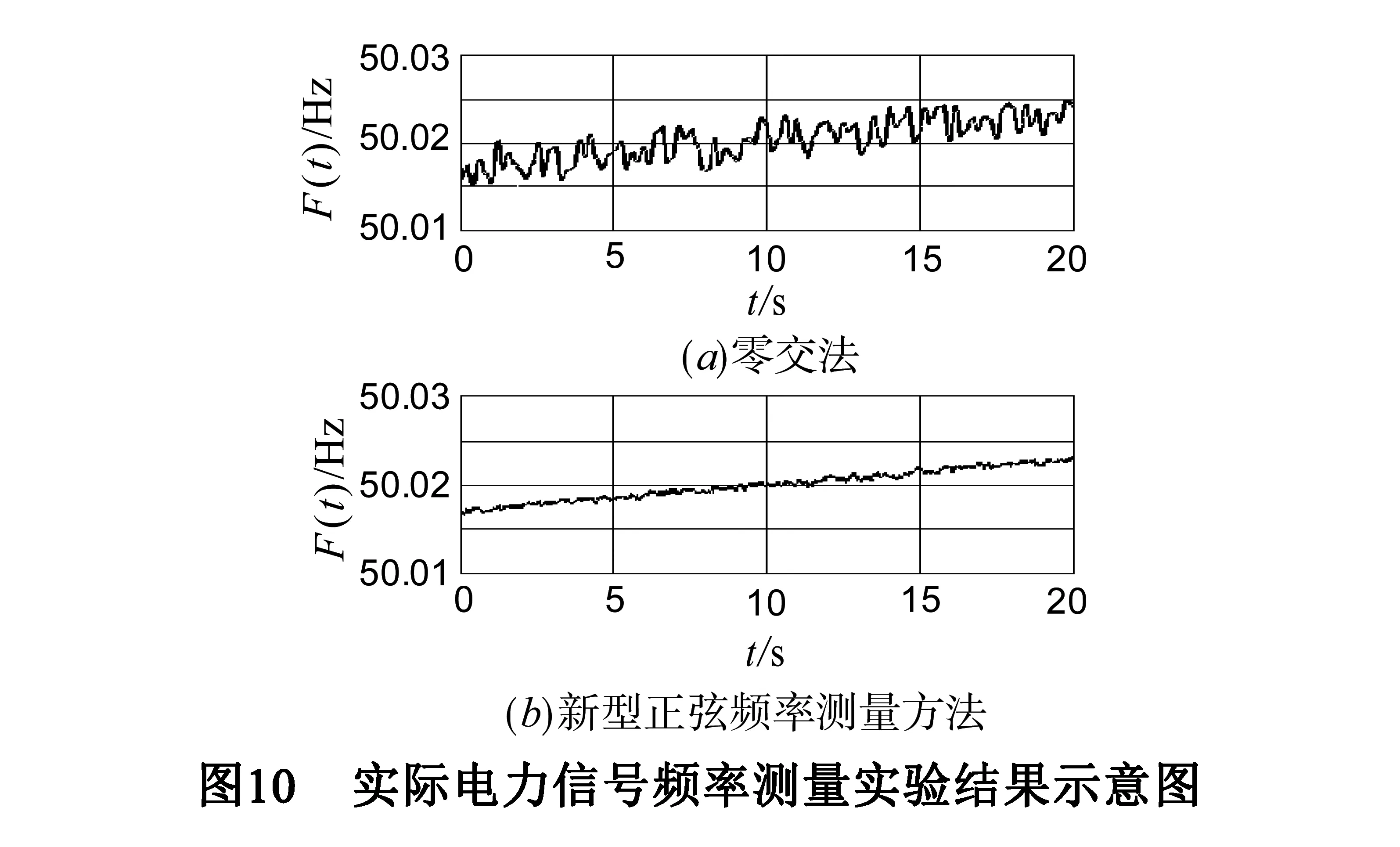
图10所示,在20s时间内,信号频率呈缓慢变化趋势,采用新型正弦频率计算方法得到结果的波动幅度相对较小,而“零交法”频率测量结果的波动幅度相对较大,可见新型正弦频率计算方法能够更真实的反映实际频率变化趋势.

8 结语

文章提出了一种新型的正弦频率测量方法,分析了正向序列和反褶序列精密初相位计算和将正交混频用于序列相位计算的原理,指出了混频干扰频率是造成正弦参数计算误差的主要内在原因,文中设计的针对混频干扰频率抑制的数字滤波,本质上是多矩形窗口特性的合成,能够对混频干扰频率影响进行深度抑制.此外,还分析了根据序列全相位差进行正弦频率计算的原理.新方法提高了谐波噪声干扰环境下的正弦相位计算和正弦频率测量的准确度.文章通过数学计算、仿真试验和物理实验结果证明了新型正弦频率测量方法的正确性和可靠性,所提出的方法在科学研究、系统正弦频率和正弦相位的测量、低频率范围精密测量仪器的研制等多方面具有重要的用途和参考价值.

[1]李军,万文军,刘志刚,等.一种基于时域响应的控制系统频率特性分析方法[J].中国电机工程学报,2012,29(10):116-122.

Li Jun,Wan Wenjun,Liu Zhigang,et al.A method of frequency domain analysis for control system based on process response in time domain[J]．Proceedings of the CSEE,2012,29(10):116-122.(in Chinese)

[2]李军,万文军,刘志刚.一种阶跃函数在矩形时间窗口频域特性的分析方法[J].电力自动化设备,2013,(11):111-116.

Li Jun,Wan Wenjun,Liu Zhigang.A method for analyzing frequency characteristics of the step function in rectangular time window[J].Electric Power Automation Equipment,2013,(11):111-116.(in Chinese)

[3]万文军,李军.一种基于LCR发散振荡响应的控制系统频率特性辨识方法[J],电机与控制学报,2014,(11):112-118.

Wan Wenjun,Li Jun.A method of frequency domain identification for control system based on process response in LCR diverging oscillation[J].Electric Machines and Control,2014,(11):112-118.(in Chinese)

[4]Jindapetch N,Chewae S,PhuKpattaranont P.FPGA implement-tations of an ADALINE adaptive filter for power-line noise cancellation in surface electromyography signal[J].Measure-ment,2012,45(3):405-414.

[5]Punchalard R.Mean square error analysis of unbiased modified plain gradient algorithm of second-order adaptive IIR notch filter[J].Signal Processing,2012,92(11):2815-2820.

[6]肖遥,孟·让·柯洛德.电力系统频率测量误差成因分析[J].电网技术,2002,26(1):39-42.

Xiao Yao,Maun Jean-Claude.Analsis on error in power sysytem frequency measurenent[J].Power System Technology,2002,26(1):39-42.(in Chinese)

[7]牛胜锁,梁志瑞,张建华,等.基于三线谱线插值FFT的电力谐波分析算法[J].中国电机工程学报,2012,32(16):130-136.

NIU Shengsuo,LIANG Zhirui ZHANG Jianhua,et al.An algorithm for electrical harmonic analysis based on triple-line interpolation FFT[J].Proceedings of the CSEE.2012,32(16):130-136.(in Chinese)

[8]肖鲲,王莉娜,M.KhurramShahzad.基于三线DFT的航空电源频率实时检测算法[J].电工技术学报,2012,27(10):190-195.

Xiao Kun,Wang Lina,M.Khurram Shahzad.Real-time frequency estimation of aircraft oower source based on 3-line DFT[J].Transactions of China Electrotechnical Sosiety,2012,27(10):190-195.(in Chinese)

[9]李明,涂亚庆,沈廷鳌,杨辉跃.自适应陷波滤波器频率估计新方法及性能分析[J].电子学报,2014,42(1):49-57.

LI Ming,TU Ya-qing,SHEN Ting-ao,YANG Hui-yue.A new frequency estimation method based on adaptive notch filter and its performance analysis[J].Acta Electronica Sinica,2014,42(1):49-57.(in Chinese)

[10]邓振淼;刘渝.正弦波频率估计的牛顿迭代方法初始值研究[J].电子学报,2007,35(1):104-107.

DENG Zhen-miao;LIU Yu.The starting point problem of sinusoid frequency estimation based on newton’s method[J].Acta Electronica Sinica,2007,35(1):104-107.(in Chinese)

[11]朱锋峰,任震,黄雯莹.基于小波变换修正幅值的电力系统频率偏移诊断方法[J].电网技术,2004,11(6):34-37.

Zhu Feng-feng,Ren Zhen,HUANG Wen-ying.A method to diagnose frequency shift of power system based on modified amplitude of wavelet transform[J].Power System Technology,2004,11(6):34-37.(in Chinese)

[12]韩建群.一种减小Duffing系统可检测断续正弦信号频率范围的方法[J].电子学报,2013,41(4):733-738.

HAN Jian-qun.A method of narrowing frequency range of intermittent sine signal detected by duffing system[J].Acta Electronica Sinica,2013,41(4):733-738.(in Chinese)

[13]黄龙庭,吴云韬,廖桂生,等.基于子空间和投影分离的三维正弦信号频率估计算法[J].电子学报,2012,40(6):1223-1228.

HUANG Long-ting,WU Yun-tao,LIAO Gui-sheng,et al.3-D Frequency estimation of multiple sinusoids using subspace and projection separation approaches[J].Acta Electronica Sinica,2012,40(6):1223-1228.(in Chinese)

[14]周卫平,吴正国,夏立.基波相位和频率的高准确度检测及在有源电力滤波器中的应用[J].中国电机工程学报,2004,24(4):91-96.

Zhou Weiping,Wu Zhengguo,Xia Li.Harmonic and reactive current detection in apf based on high-accuracy phase and frequency detection[J].Proceedings of the CSEE,2004,24(4):91-96.(in Chinese)

[15]李军,王越超.一种基于幅值调制的新型电力系统正弦频率测量方法[J].电工技术学报,2015,30(7):144-150.

LI Jun,WANG Yuechao.A novel power system sinusoidal frequency measurement method based on amplitude modulation[J].Power System Technology,2015,30(7):144-150.(in Chinese)

[16]雷银照.我国供用电频率50Hz的起源[J].电工技术学报,2010,25(3):21-26.

Lei Yinzhao.The origins of 50Hz power frequency in mainland china[J].Transactions of China Electrotechnical Sosiety,2010,25(3):21-26.(in Chinese)

李 军 男，1962年10月出生,湖北应城人,1983年从西安空军工程大学电讯工程学院专科毕业, 2001年从87389部队转业进入广东电网有限责任公司电力科学研究院工作,现为工程师,长期从事计算机控制与通讯等试验研究工作.

E-mail:lijun-87389@163.com

王越超 男，1978年3月出生，辽宁沈阳人，2012年广东工业大学博士毕业,现在广东电网有限责任公司电力科学研究院博士后入站工作，现为工程师，长期从事计算机控制与数据分析等科学研究工作.

E-mail:20111404@qq.com

A Novel Sinusoidal Frequency Measurement Method Based on Precise Calculation of Initial Phase of Sequence and Deconvolution Sequence

LI Jun,WANG Yue-chao,LI Feng

(ElectricPowerResearchInstituteofGuangdongPowerGridCompang,Ltd,Guangzhou,Guangdong510080,China)

Sinusoidal frequency is one of the basic parameters.The high-accuracy sinusoidal frequency measurement technology has wide applications.But in the aspect of low-frequency sinusoidal frequency measurement,the current sinusoidal frequency measurement technology usually has the defects of low accuracy under the environment of harmonic noise interference.This paper proposes a novel sinusoidal frequency measurement method based on precise calculation of initial phase by means of sequence and deconvolution sequence.The measurement principles of precise initial phase sequence calculation and orthogonal mixing calculation for sequence phase measurement are analyzed.It is pointed out that the mixed-frequency interference is the main cause of the measurement error.By severely inhibiting the interference of mixed-frequency,and by calculating the full phase difference of sequence and deconvolution sequence,accuracy of sinusoidal frequency measurement is improved under the environment of harmonic noise interference.Mathematical calculation,simulation test and the physical experiment results also verify the correctness and reliability of the proposed method.

deconvolution sequence;precise initial phase calculation;full phase difference of sequence;quadrature mixer;mixing interference frequency;digital filter

2015-02-03;

2015-08-03;责任编辑:马兰英

TN74

A

0372-2112 (2016)10-2370-07

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.10.013