基于污染二维混沌动力系统的加密算法

王 丽 燕， 柳 扬

( 大连大学 信息工程学院， 辽宁 大连 116622 )



基于污染二维混沌动力系统的加密算法

王 丽 燕*， 柳 扬

( 大连大学 信息工程学院， 辽宁 大连 116622 )

首先定义了污染动力系统，将二维Henon动力系统用二维Logistic动力系统进行污染，用这个污染的二维混沌动力系统构造序列密码体系．这种算法可以产生两列密钥，从而有效地解决了输出结果对密钥低bit位变化敏感度较低的问题．计算机模拟实验和游程测试、相关性分析、灵敏度分析、平衡度检验等安全实验分析结果表明，密文、明文和密钥之间具有高度的非线性和敏感性，算法的密钥空间巨大，可以有效防止统计攻击、唯密文攻击和穷举攻击．

污染动力系统；二维Henon动力系统；二维Logistic动力系统；序列密码

0 引 言

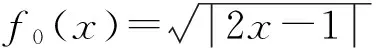
为增强混沌动力系统的敏感性，本文借用污染分布的思想，给出污染动力系统的定义，将二维Henon动力系统用二维Logistic动力系统进行污染，讨论污染后动力系统的简单性质．基于该污染的二维混沌系统产生两列密钥流对明文进行加密，通过游程测试、相关性分析、灵敏度分析、平衡度检验等计算机模拟实验对安全性进行验证．

1 混沌动力系统

1.1 污染混沌动力系统

定义1 设f1和f2是两个动力系统，称f=αf1+(1-α)f2为污染动力系统，其中α(0<α<1)称为污染系数．

1.2 污染二维混沌动力系统

二维Logistic映射动力学方程为

xn+1=μλ1xn(1-xn)+γyn

yn+1=μλ2yn(1-yn)+γxn

(1)

其中λ1、λ2、γ、μ是参数．当μ=4时，表1列出了系统会出现混沌现象的不同条件[12]．

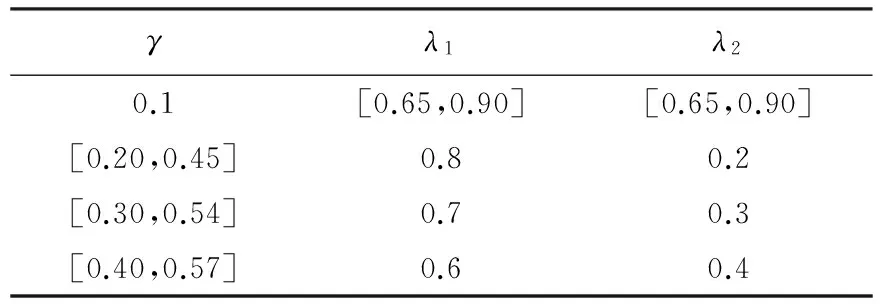
表1 二维Logistic映射混沌条件

图1分别给出了两种参数取值条件下的分叉情况．

二维Henon映射的动力学方程为

(2)

其中p、q为参数．图2给出了p=1.4，q=0.3条件下的混沌状态图．

将二维Henon映射用二维Logistic映射进行污染，得到污染动力系统：

(3)

其中0<α<1．

(a) λ1, λ2=1-λ1, λ=0.3

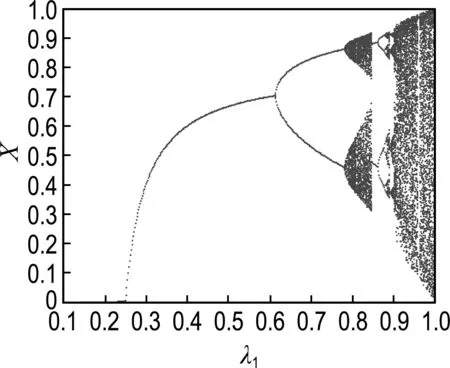
(b)λ1=λ2,λ=1-λ1

图1 Logistic映射分叉图

Fig.1 Branch chart of Logistic mapping

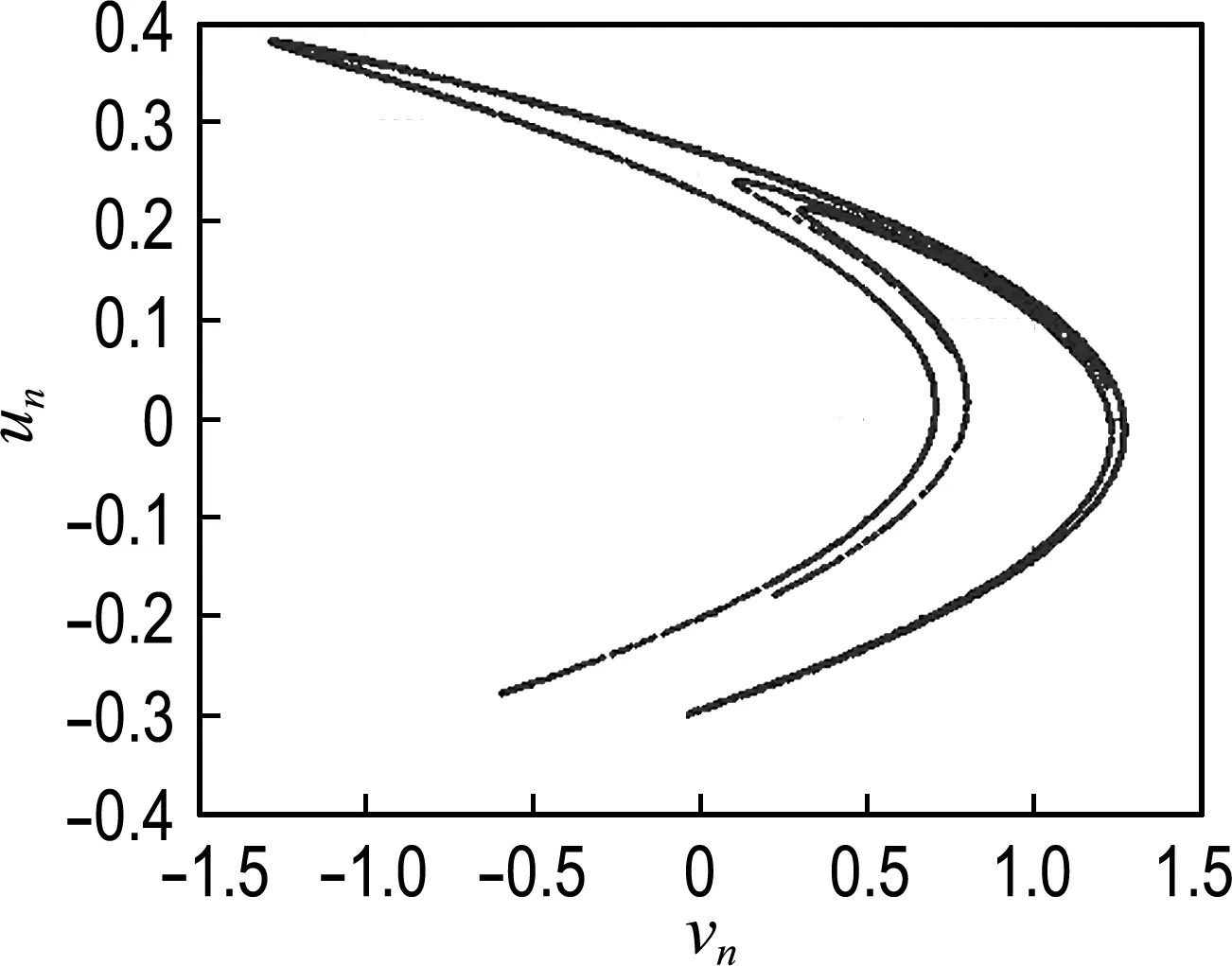
图2 Henon映射的吸引子

利用Matlab计算，得到Jacobi矩阵的特征值的绝对值为1.871 9>1，根据差分方程组计算Lyapunov指数定义[13]，可知式(3)的Lyapunov指数大于零，说明污染的二维动力系统(3)为混沌动力系统．系统输出的x(n)和y(n)的值如图3所示，容易看出输出值服从均匀分布．

(a) x(n)

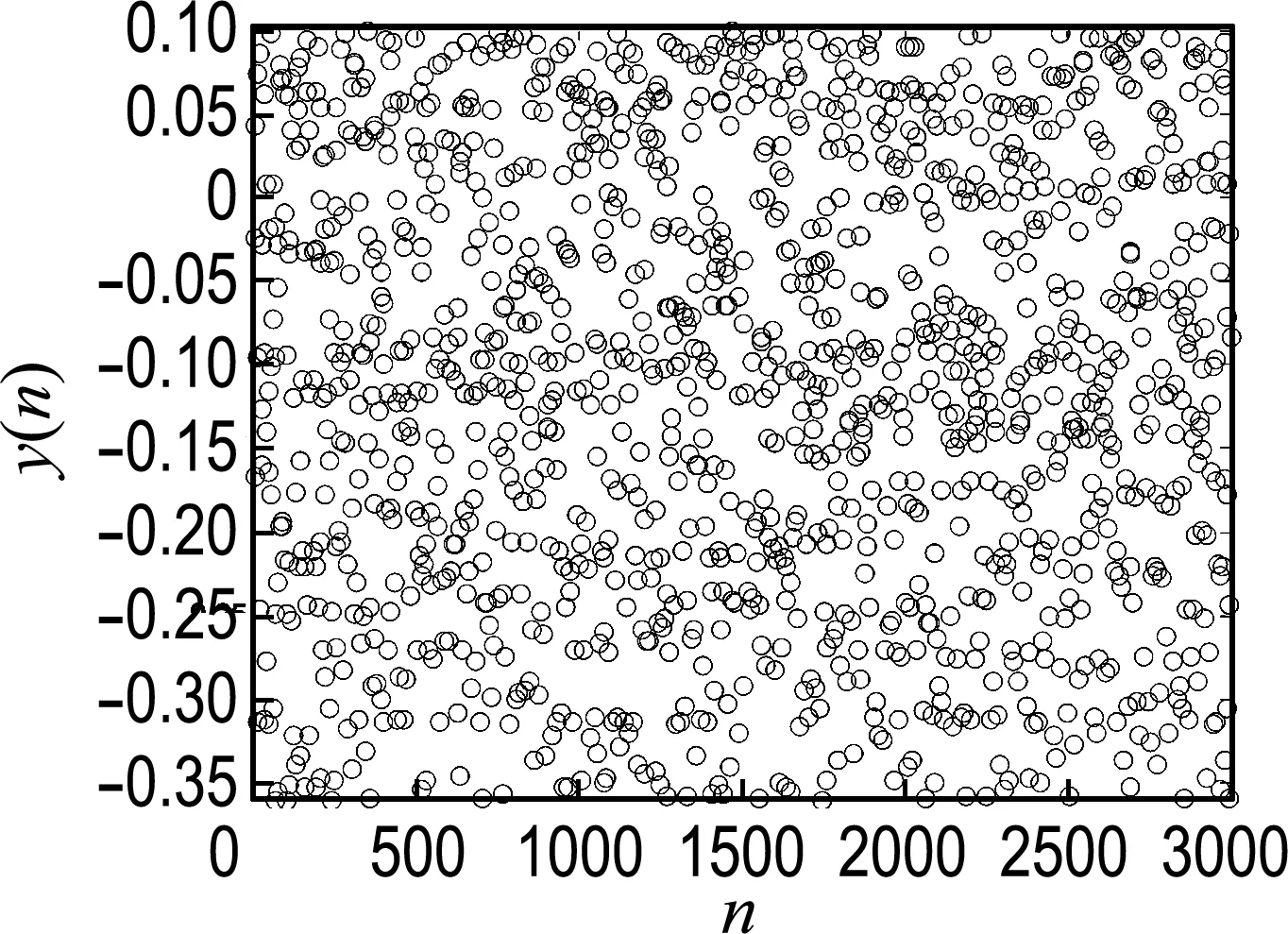
(b)y(n)

图3x(n)和y(n)在其区间的分布

Fig.3 The distribution ofx(n) andy(n) in their domains

2 序列密码的加密与解密算法

2.1 加密算法

加密过程如图4所示．

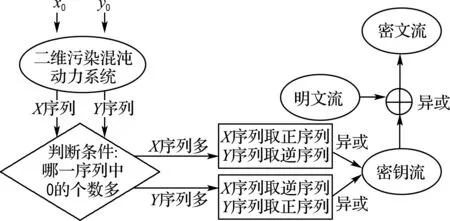
图4 加密过程

具体加密算法如下：

(1)通过ASCII码把明文转化为十六位二进制序列{m1m2m3…mn}，其中mi(i=1,2,3,…,n)为0或者1．

(2)确定密钥．给二维污染混沌动力系统(3)中的参数μ、γ、λ1、λ2、p、q、α取值，选定迭代初始值x0、y0，迭代得到两个混沌序列{x(i)}(i=1,2,3,…,n)和{y(j)}(j=1,2,3,…,n)．

(3)由离散化算子Tk(x(i))=[10kx(i)]mod 2和Tk(y(j))=[10ky(j)]mod 2，计算得到两个密钥序列{k(i)}和{k(j)}，其中k(i)=Tk(x(i))(i=1,2,3,…,n)，k(j)=Tk(y(j))(j=1,2,3,…,n)．

(4)比较两个密钥序列{k(i)}(i=1,2,3,…,n)和{k(j)}(j=1,2,3,…,n)中0的个数，个数多的取正序列，个数少的取逆序列，然后将这两个序列异或，得到新的密钥序列{k(l)}(l=1,2,3,…,n)．

(5)将密钥序列{k(l)}(l=1,2,3,…,n)与明文序列{m1m2m3…mn}进行异或运算，得到密文二进制序列{c1c2c3…cn}．

(6)由密文序列C=c1c2c3…cn的ASCII值得到最终的密文．

类似地可以给出解密算法．

2.2 算法仿真

“二维污染混沌动力系统”明文的二进制序列为

01001110100011000111111011110100011011

00011000010110011111010011011011011111

01110110110010001100010100101010100001

01001010011011011111001111101101111110

11011111

不同条件下得到的密文如下：

(1)若取μ=4，γ=0.52，λ1=0.7，λ2=0.3，p=1.4，q=0.3，α=0.02，x0=0.131 4，y0=0.112 3，j=4，得到的密文为

(2)若取α=0.02+10-11，其他条件与(1)相同，密文为

(3)若取y0=0.112 3+10-11，其他条件与(1)相同，密文为

(4)若取x0=0.131 4+10-11，其他条件与(1)相同，密文为

(5)若取x0=0.131 4+10-11,y0=0.112 3+10-11，其他条件与(1)相同，密文为

(6)若取j=7，其他条件与(1)相同，密文为

(7)若取x0=0,y0=0，其他条件与(1)相同，密文为

(8)若取γ=0.52+10-7，x0=0，y0=0，j=4，其他条件与(1)相同，密文为

图5给出了以上8种条件下密文用0-1序列的图形化表示, 显然，密钥的细微改变将会导致密文的显著改变．

3 安全性分析

3.1 游程测试[13]

游程是指序列中由相同bit所构成的不间断的子序列．该测试可以判断其是否为随机序列．

具体测试方法如下：

步骤4 计算判断标准P：

如果P<0.01，断定测试的序列随机性较差；反之，断定序列具有较好的随机性．

若选取μ=4，γ=0.52，λ1=0.7，λ2=0.3，p=1.4，q=0.3，α=0.02，x0=0.131 4，y0=0.112 3，j=4，n=160，计算得到x(n)序列和y(n) 序列的P都为1.99，远大于0.01．因此，可以认为混沌序列是随机序列．

3.2 相关性分析

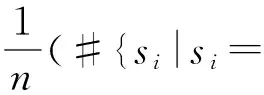
本文选取长度n=10 000的0序列作为明文，以动力系统(3)参数值μ=4，γ=0.52，λ1=0.7，λ2=0.3，p=1.4，q=0.3，α=0.02，x0=0.131 4，y0=0.112 3，j=4为例，对明文进行加密，相关度情况如图6所示．

显然随着n的增大，相关度逐渐趋近于0，说明密文与明文几乎不相关．

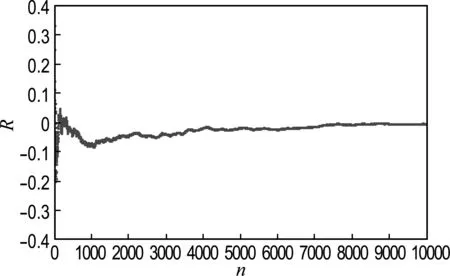
图6 明文与密文的相关度

3.3 灵敏度分析

如果明文表示为{m1m2m3…mn}，密文表示为{s1s2s3…sn}，其中mi和si只取0或1，i=1,2,3,…,n，称

为明文与密文间的灵敏度[27]．

仍以长度n=10 000的0序列作为明文，动力系统(3)参数值μ=4，γ=0.52，λ1=0.7，λ2=0.3，p=1.4，q=0.3，α=0.02，x0=0.131 4，y0=0.112 3，j=4为例，对明文进行加密，密文与明文间的灵敏度情况如图7所示．

图7 灵敏度分析图

图7表明，相比明文，大致50%的密文序列将会改变．

3.4 密文的平衡度检验

仍以长度n=10 000的0序列作为明文，动力系统(3)参数值μ=4，γ=0.52，λ1=0.7，λ2=0.3，p=1.4，q=0.3，α=0.02，x0=0.131 4，y0=0.112 3，j=4为例，对明文进行加密，密文序列中0-1平衡度如图8所示．

图8 平衡度分析图

图8的结果表明，序列位数越多，平衡度的值就越趋近于0，说明序列中1和0的个数几乎相等．

3.5 密钥空间分析

本文选取的密钥是污染二维混沌动力系统随机产生的初值x0、y0和离散化算子以及污染系数α，假设计算的精度为10-5，采用本算法形成的密钥空间至少为1020．实际上，动力系统本身的参数μ、γ、λ1、λ2、p、q只要在可以形成混沌的范围内取值，都可以作为密钥．而且计算机的计算精度远远超过10-5，这样密钥空间将大大超过1020．本算法足够抵抗由于密钥空间不大而形成的穷举攻击．

4 结 语

本文给出污染混沌动力系统的概念，并用污染系数α将二维Henon动力系统用二维Logistic动力系统进行污染，并进一步用污染后的多参数动力系统构造序列密码的加密算法．所进行的各项性能分析，如随机性分析、相关性分析、灵敏度分析、0-1平衡度检验等都表明污染的混沌映射具有良好统计特性，而且密钥空间巨大，可以有效防止统计攻击、唯密文攻击和穷举攻击．

[1] Matthews R A J. On the derivation of a ″chaotic″ encryption algorithm [J]. Cryptologia, 1984, 8(1):29-41.

[2] Habutsu T, Nishio Y, Sasase I,etal. A secret key cryptosystem by iterating a chaotic map [C] // Davies D W, ed. Advances in Cryptology - EUROCRYPT ′91, LNCS 547. Berlin:Springer-Verlag, 1991:127-140.

[3] Biham E. Cryptanalysis of the chaotic map cryptosystem suggested at EUROCRYPT′91 [C]// EUROCRYPT′91 Proceedings of the 10th Annual International Conference on Theory and Application of Cryptographic Techniques. Berlin:Springer-Verlag, 1991:532-534.

[4] 周 红,罗 杰,凌燮亭. 混沌非线性反馈密码序列的理论设计和有限精度实现[J]. 电子学报, 1997, 25(10):57-60.

ZHOU Hong, LUO Jie, LING Xie-ting. Generating nonlinear feedback stream ciphers via chaotic systems [J]. Acta Electronica Sinica, 1997, 25(10):57-60. (in Chinese)

[5] 周 红,俞 军,凌燮亭. 混沌前馈型流密码的设计[J]. 电子学报, 1998, 26(1):98-101.

ZHOU Hong, YU Jun, LING Xie-ting. Design of chaotic feed forward stream cipher [J]. Acta Electronica Sinica, 1998, 26(1):98-101. (in Chinese)

[6] 桑 涛,王汝笠,严义埙. 一类新型混沌反馈密码序列的理论设计[J]. 电子学报, 1999, 27(7):47-50.

SANG Tao, WANG Ru-li, YAN Yi-xun. The theoretical design for a class of new chaotic feedback stream ciphers [J]. Acta Electronica Sinica, 1999, 27(7):47-50. (in Chinese)

[7] 孙 枫,秦红磊,徐耀群,等. 基于混沌的分组密码置换网络的设计[J]. 中国工程科学, 2000, 2(9):47-49.

SUN Feng, QIN Hong-lei, XU Yao-qun,etal. Design of block cipher substitution network on chaos [J]. Engineering Science, 2000, 2(9):47-49. (in Chinese)

[8] 王相生,甘骏人. 一种基于混沌的序列密码生成方法[J]. 计算机学报, 2002, 25(4):351-356.

WANG Xiang-sheng, GAN Jun-ren. A chaotic sequence encryption method [J]. Chinese Journal of Computers, 2002, 25(4):351-356. (in Chinese)

[9] 翁贻方,鞠 磊. 基于混沌的序列密码加密算法[J]. 计算机工程, 2002, 28(11):79-80, 83.

WENG Yi-fang, JU Lei. Chaotic stream cipher encryption algorithms [J]. Computer Engineering, 2002, 28(11):79-80, 83. (in Chinese)

[10] 李红达,冯登国. 基于复合离散混沌动力系统的序列密码算法[J]. 软件学报, 2003, 14(5):991-998.

LI Hong-da, FENG Deng-guo. Stream cipher algorithms based on composite nonlinear discrete chaotic dynamical systems [J]. Journal of Software, 2003, 14(5):991-998. (in Chinese)

[11] 李红达,冯登国. 复合离散混沌动力系统与序列密码体系[J]. 电子学报, 2003, 31(8):1209-1212.

LI Hong-da, FENG Deng-guo. Composite nonlinear descrete chaotic dynamical systems and stream cipher systems [J]. Acta Electronica Sinica, 2003, 31(8):1209-1212. (in Chinese)

[12] Gotz M, Kelber K, Schwarz W. Discrete-time chaotic encryption systems. I. Statistical design approach[J]. IEEE Transactions on Circuits and Systems. I. Fundamental Theory and Applications, 1997, 44(10):963-970.

[13] Kocarev L. Chaos-based cryptography:A brief overview [J]. IEEE Circuits and Systems Magazine, 2002, 1(3):6-21.

[14] XIANG Tao, Wong Kwor-kwo, LIAO Xiao-feng. A novel symmetrical cryptosystem based on discretized two-dimensional chaotic map [J]. Physics Letters A, 2007, 364(3-4):252-258.

[15] Alvarez G, Montoya F, Romera M,etal. Cryptanalysis of a chaotic encryption system [J]. Physics Letters A, 2000, 276(1-4):191-196.

[16] 张 斌,金晨辉. 对迭代型混沌密码的逆推压缩攻击[J]. 电子学报, 2010, 38(1):129-134,140.

ZHANG Bin, JIN Chen-hui. Inversion and compression attacks to iterative chaotic ciphers [J]. Acta Electronica Sinica, 2010, 38(1):129-134,140. (in Chinese)

[17] 汪海明,李 明,金晨辉. 对XW混沌密码算法的分割攻击[J]. 计算机应用研究, 2010, 27(7):2625-2628.

WANG Hai-ming, LI Ming, JIN Chen-hui. Divide-and-conquer attack on XW chaotic cipher [J]. Application Research of Computers, 2010, 27(7):2625-2628. (in Chinese)

[18] 尹汝明,袁 坚,山秀明,等. 混沌密码系统弱密钥随机性分析[J]. 中国科学:信息科学, 2011, 41(7):777-788.

YIN Ru-ming, YUAN Jian, SHAN Xiu-ming,etal. Weak key analysis for chaotic cipher based on randomness properties [J]. Science in China:Information Sciences, 2011, 41(7):777-788. (in Chinese)

[19] 金晨辉. 一个基于混沌的分组密码算法的分析[J]. 中国工程科学, 2001, 3(6):75-80.

JIN Chen-hui. Analysis of a block cipher based on chaos [J]. Engineering Science, 2001, 3(6):75-80. (in Chinese)

[20] 金晨辉,高海英. 对两个基于混沌的序列密码算法的分析[J]. 电子学报, 2004, 32(7):1066-1070.

JIN Chen-hui, GAO Hai-ying. Analysis of two stream ciphers based on chaos [J]. Acta Electronica Sinica, 2004, 32(7):1066-1070. (in Chinese)

[21] 金晨辉,杨 阳,祁传达. 对混沌序列密码的相关密钥攻击[J]. 电子与信息学报, 2006, 28(3):410-414.

JIN Chen-hui, YANG Yang, QI Chuan-da. A related-key attack on chaotic stream ciphers [J]. Journal of Electronics & Information Technology, 2006, 28(3):410-414. (in Chinese)

[22] 王丽燕,李永华,贾思齐,等. 一种基于复合混沌动力系统的序列密码算法[J]. 大连理工大学学报, 2012, 52(5):730-735.

WANG Li-yan, LI Yong-hua, JIA Si-qi,etal. A stream cipher algorithm based on composite chaotic dynamical systems [J]. Journal of Dalian University of Technology, 2012, 52(5):730-735. (in Chinese)

[23] 孙小雁,张焕国,张茂胜,等. Logistic混沌扰动三角形密码体制[J]. 计算机应用与软件, 2014, 31(9):268-271.

SUN Xiao-yan, ZHANG Huan-guo, ZHANG Mao-sheng,etal. Triangular cryptosystem with Logistic chaos disturbance [J]. Computer Applications and Software, 2014, 31(9):268-271. (in Chinese)

[24] 王丽燕,许佳佳,李海燕. 基于两个离散混沌动力系统的序列密码算法[J]. 大连理工大学学报, 2014, 54(5):581-588.

WANG Li-yan, XU Jia-jia, LI Hai-yan. A stream cipher algorithm based on two discrete chaotic dynamical systems [J]. Journal of Dalian University of Technology, 2014, 54(5):581-588. (in Chinese)

[25] 张 顺,高铁杠. 基于类DNA编码分组与替换的加密方案[J]. 电子与信息学报, 2015, 37(1):150-157.

ZHANG Shun, GAO Tie-gang. Encryption based on DNA coding, codon grouping and substitution [J]. Journal of Electronics & Information Technology, 2015, 37(1):150-157. (in Chinese)

[26] Merah L, Ali-Pacha A, Naima H-S. Real-time cryptosystem based on synchronized chaotic system [J]. Nonlinear Dynamics, 2015, 82(1-2):877-890.

[27] 廖晓峰,肖 迪,陈 勇,等. 混沌密码学原理及其应用[M]. 北京:科学出版社, 2009.

LIAO Xiao-feng, XIAO Di, CHEN Yong,etal. Theory and Applications of Chaotic Cryptography [M]. Beijing:Science Press, 2009. (in Chinese)

Encryption algorithm based on contaminated two-dimensional chaotic dynamic system

WANG Li-yan*, LIU Yang

( College of Information Engineering, Dalian University, Dalian 116622, China )

An algorithm to construct a stream cipher system is presented by defining a contaminated dynamic system, in which the two-dimensional Henon dynamic system is contaminated by the two-dimensional Logistic dynamic system. By generating two columns of keys, this algorithm can effectively solve the problem that the output is not very sensitive to the change of the low bit of the input. The results of safety tests, such as computer simulation, runs test, correlation analysis, sensitivity analysis and balance test, etc. show the highly nonlinearity and sensitivity among ciphertext, plaintext and the key. Also the large key space of this algorithm can effectively prevent the statistical attacks, ciphertext only attacks and exhaustive attacks.

contaminated dynamic system; two-dimensional Henon dynamic system; two-dimensional Logistic dynamic system; stream cipher

2016-01-19；

2016-09-02．

国家自然科学基金资助项目(71072161)．

王丽燕*(1963-)，女，博士，教授，E-mail:wly1963@163.com；柳 扬(1979-)，女，博士生，E-mail:lykx2001@163.com.

1000-8608(2016)06-0650-07

TN918

A

10.7511/dllgxb201606014