四叶树Hosoya指标显式公式及其序列

杨 利 民， 段 丽 燕， 王 天 明

( 1.大理大学 数学与计算机学院, 云南 大理 671003；2.大连理工大学 数学科学学院, 辽宁 大连 116024 )



四叶树Hosoya指标显式公式及其序列

杨 利 民*1， 段 丽 燕1， 王 天 明2

( 1.大理大学 数学与计算机学院, 云南 大理 671003；2.大连理工大学 数学科学学院, 辽宁 大连 116024 )

为研究四叶树Hosoya指标的规律，利用图论的分支分析法，解决了四叶树Hosoya指标的显式公式和序列．对于一般的t叶树，仍然用同样分支分析法，得到相应的t叶树Hosoya指标的显式公式和序列．发现了一族初值不一样的Fibonacci序列，在科学上对组合数学和图论提供了一定参考．

四叶树；t叶树；S(n)-因子；Fibonacci数；Hosoya指标

0 引 言

四叶草又名幸运草，是三叶草或苜蓿草的稀有变种．苜蓿草，是多年生草本植物，一般只有三片小叶子，叶形呈心形，叶心较深色的部分亦是心形．最为有趣也最特别的是，在十万株苜蓿草中，可能只会发现一株是四叶草，因为概率是十万分之一，四叶草成为国际公认的幸运的象征．

由四叶草引出四叶树，四片叶子、顶点数为n的树叫做四叶树．

Fibonacci数列，也称为“兔子数列”，其数列为0，1，1，2，3，5，8，13，21，34，55，89，144，…，满足递归关系式Fn=Fn-1+Fn-2，初值F0=0，F1=1[1-3]．

本文研究四叶树Hosoya指标的显式公式和序列．

1 定义和引理

1.1 定 义

定义1[4]设S(n)={Ki：1≤i≤n}(n≥1)，Ki是i个顶点的完全图．假设M是G的子图并且M的每一个分支都同构于S(n)={Ki：1≤i≤n}(n≥1)中的某一个元素，则称M为图G的一个S(n)={Ki：1≤i≤n}-子图．假设M是图G的生成子图，则称M为图G的一个S(n)={Ki：1≤i≤n}-因子．

令A(G)是图G的所有S(n)={Ki：1≤i≤n}-因子个数．图G是简单图，不包括多重边和环．

定义2 图G的所有k-匹配个数称作Hosoya指标．Hosoya指标用Z(G)表示．

1.2 基本引理

引理2 如果G和H的交为空图，即G∩H=∅，则A(G∪H)=A(G)·A(H)．

引理3[5]假设Pn是长为n的路，且有n+1个顶点，则Pn的S(n)={Ki：1≤i≤n}-因子个数是A(Pn)=Fn+2(n≥1)，其中Fn+2是第n+2个Fibonacci数．

引理4[6]假设图G的顶点数为n并且无K3子图，则Hosoya指标Z(G)等于图G的所有S(n)={Ki：1≤i≤n}-因子个数：Z(G)=A(G)．

2 主要结果

2.1 四叶树Hosoya指标的显式公式

下面给出四叶树的Hosoya指标的显式公式并证明[7-8]．

定理1 如图1所示n个顶点的四叶树，它的Hosoya指标为

Z(G1)=5Fn-4+Fn-5；n≥5

图1 四叶树图G1

证明 利用图的分支分析法[9-10]，对给定点Vn-4进行分析，过Vn-4顶点的一切完全图只有K1和5个K2，无Ki(3≤i≤n)，讨论分3种情况：

情况一 过Vn-4点完全图为K1，即为点Vn-4，Vn-4作为一个完全分支，则S(n)-因子个数如下：

A(G1-V(K1))=

A(Vn-3∪Vn-2∪Vn-1∪Vn∪Pn-6)=

A(Vn-3)A(Vn-2)A(Vn-1)A(Vn)A(Pn-6)=

1×1×1×1×A(Pn-6)=A(Pn-6)

根据引理3就有

A(G1-V(K1))=Fn-4

情况二 过Vn-4点完全图为vn-4vn-3，vn-4vn-2，vn-4vn-1和vn-4vn，这4个完全图K2是对称的，K2作为两个点的完全分支，则S(n)-因子个数如下：

4A(G1-V(K2))=

4A(Vn-2∪Vn-1∪Vn∪Pn-6)=

4A(Vn-2)A(Vn-1)A(Vn)A(Pn-6)=

4×1×1×1×A(Pn-6)=4Fn-4

情况三 过Vn-4点完全图为vn-5vn-4，K2作为两个点的一个完全分支，则S(n)-因子个数如下：

“我说我快要活不成了。”我失去了与他斗嘴的乐趣和力气，我的眼前一阵阵发黑，手腕处那种汩汩的声音让我觉得害怕。

A(G1-V(K2))=

A(Vn-3∪Vn-2∪Vn-1∪Vn∪Pn-7)=

A(Vn-3)A(Vn-2)A(Vn-1)A(Vn)A(Pn-7)=

1×1×1×1×A(Pn-7)=A(Pn-7)=Fn-5

据引理1得到

A(G1-V(K1))+4A(G1-V(K2))+

A(G1-V(K2))=

Fn-4+4Fn-4+Fn-5=5Fn-4+Fn-5

Z(G1)=A(G1)=5Fn-4+Fn-5；n≥5

有趣的是，四叶树序列的初值f0=5，f1=6，通项fn=fn-1+fn-2，这好像是Fibonacci序列，只是初值不一样．下面将证明这个规律是对的．

证明 因为fn=5Fn-4+Fn-5，所以fn-1=5Fn-5+Fn-6，fn-2=5Fn-6+Fn-7，又因为fn-1+fn-2=5(Fn-5+Fn-6)+(Fn-6+Fn-7)=5Fn-4+Fn-5，则fn=fn-1+fn-2．

□

Tab.1 Some initial values of Hosoya index of four

nZ(T4n)nZ(T4n)55928661045711117381712118

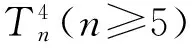
5，6，11，17，28，45，73，118，191，309，500，809，1 309，2 118，3 427，5 545，8 972，14 517，23 489，38 006，61 495，99 501，160 996，260 497，421 493，681 990，1 103 483，…

2.2 t叶树Hosoya指标的显式公式

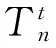
定理2 如图2所示n个顶点、t片树叶的t叶树，它的Hosoya指标为

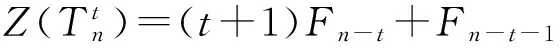
图2 t叶树

证明 利用图的分支分析法，对给定点Vn-t进行分析，过Vn-t顶点的一切完全图只有K1和(t+1)个K2，无Ki(3≤i≤n)，讨论分3种情况：

情况一 过Vn-t点完全图为K1，即为点Vn-t，Vn-t作为一个完全分支，则S(n)-因子个数如下：

A(Vn-t+1∪Vn-t+2∪…∪Vn∪Pn-t-2)=

A(Vn-t+1)A(Vn-t+2)…A(Vn)A(Pn-t-2)=

1×1×…×1×A(Pn-t-2)=A(Pn-t-2)

根据引理3有

情况二 过Vn-t点完全图为vn-tvn-t+1，vn-tvn-t+2，…，vn-tvn，这t个完全图K2是对称的，K2作为两个点的完全分支，则S(n)-因子个数如下：

tA(Vn-t+2∪…∪Vn∪Pn-t-2)=

tA(Vn-t+2)…A(Vn)A(Pn-t-2)=

t×1×…×1×A(Pn-t-2)=tA(Pn-t-2)=tFn-t

情况三 过Vn-t点完全图为vn-tvn-t-1，K2作为两个点的一个完全分支，则S(n)-因子个数如下：

A(Vn-t+1∪Vn-t+2∪…∪Vn∪Pn-t-3)=

A(Vn-t+1)A(Vn-t+2)…A(Vn)A(Pn-t-3)=

1×1×…×1×A(Pn-t-3)=

A(Pn-t-3)=Fn-t-1

据引理1得到

Fn-t+tFn-t+Fn-t-1=

(t+1)Fn-t+Fn-t-1

据引理4得到

n≥t+1，t≥2

图3 二叶树

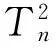
同样有趣的是，二叶树序列的初值f0=3，f1=4，通项fn=fn-1+fn-2，这好像是Fibonacci序列，只是初值不一样．下面将证明这个规律是对的．

因为fn=3Fn-2+Fn-3，所以fn-1=3Fn-3+Fn-4，fn-2=3Fn-4+Fn-5，又因为fn-1+fn-2=3(Fn-3+Fn-4)+(Fn-4+Fn-5)=3Fn-2+Fn-3，则fn=fn-1+fn-2．

□

3，4，7，11，18，29，47，76，123，199，322，521，843，1 364，2 207，3 571，5 778，9 349，…

图4 三叶树

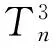
三叶树序列的初值f0=4，f1=5，通项fn=fn-1+fn-2，这好像是Fibonacci序列，只是初值不一样．下面将证明这个规律是对的．

因为fn=4Fn-3+Fn-4，所以fn-1=4Fn-4+Fn-5，fn-2=4Fn-5+Fn-6，又因为fn-1+fn-2=4(Fn-4+Fn-5)+(Fn-5+Fn-6)=4Fn-3+Fn-4，则fn=fn-1+fn-2．

□

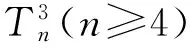
4，5，9，14，23，37，60，97，157，254，411，665，1 076，1 741，2 817，4 558，7 375，11 933，…

对于一般的t叶树，发现它的Hosoya指标序列呈现同样规律．初值f0=t+1，f1=t+2，通项fn=fn-1+fn-2．

证明 因为fn=(t+1)Fn-t+Fn-t-1，所以fn-1=(t+1)Fn-t-1+Fn-t-2，fn-2=(t+1)Fn-t-2+Fn-t-3，又因为fn-1+fn-2=(t+1)(Fn-t-1+Fn-t-2)+(Fn-t-2+Fn-t-3)=(t+1)Fn-t+Fn-t-1，则fn=fn-1+fn-2．

□

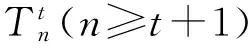
t+1，t+2，2t+3，3t+5，5t+8，8t+13，13t+21，21t+34，34t+55，…

推论3 如图5所示的五叶树的Hosoya指标为

令t=5，五叶树的Hosoya指标与t叶树的呈同样规律，初值f0=6，f1=7，通项fn=fn-1+fn-2．

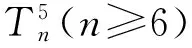
6，7，13，20，33，53，86，139，225，364，589，953，1 542，2 495，…

图5 五叶树

3 结 语

本文解决了四叶树Hosoya指标的显式公式和序列，并将它推广到一般的t叶树上，有趣的是，发现了一族初值不一样的Fibonacci序列，在科学上对组合数学和图论提供了一定参考价值．

[1] 王天明. 近代组合学[M]. 大连:大连理工大学出版社, 2008.

WANG Tian-ming. Modern Combinatorics [M]. Dalian:Dalian University of Technology Press, 2008. (in Chinese)

[2] Comtet L. 高等组合学:有限和无限展开的艺术[M]. 谭明术,杨利民,等译. 大连:大连理工大学出版社, 1991.

Comtet L. Advanced Combinatorics: The Art of Finite and Infinite Unfolding [M]. TAN Ming-shu, YANG Li-min,etal., trans. Dalian: Dalian University of Technology Press, 1991. (in Chinese)

[3] Harary F, Palmer E M. Graphical Enumeration [M]. New York: Academic Press Inc., 1973.

[4] 杨利民,王天明. 色多项式的显示公式[J]. 数学进展, 2006, 35(1):55-66.

YANG Li-min, WANG Tian-ming. The explicit formula of the chromatic polynomial [J]. Advances in Mathematics, 2006, 35(1):55-66. (in Chinese)

[5] 杨利民.S(n)={Ki:1≤i≤n}-因子数的递归关系式[J]. 数学研究与评论, 1991, 11(1):78.

YANG Li-min. A recurrence relation for the number of factors ofS(n)={Ki:1≤i≤n} [J]. Journal of Mathematical Research and Exposition, 1991, 11(1):78. (in Chinese)

[6] 杨利民,杨正亮. Fibonacci数的图论应用[J]. 大理学院学报, 2011, 10(4):12-16.

YANG Li-min, YANG Zheng-liang. Graphic applications on Fibonacci numbers [J]. Journal of Dali University, 2011, 10(4):12-16. (in Chinese)

[7] 杨利民,王天明,年四洪. 完全i部图N[(X1,X2,…,Xi),k]计数公式[J]. 大连理工大学学报, 2007, 47(6):925-930.

YANG Li-min, WANG Tian-ming, NIAN Si-hong. Counting formulas ofN[(X1,X2,…,Xi),k] of completei-partite graphs [J]. Journal of Dalian University of Technology, 2007, 47(6):925-930. (in Chinese)

[8] 杨利民. 理想子图计数及其应用[J]. 大连理工大学学报, 1989, 29(5):605-609.

YANG Li-min. Enumeration of ideal subgraphs and its applications [J]. Journal of Dalian University of Technology, 1989, 29(5):605-609. (in Chinese)

[9] YANG Li-min, WANG Tian-ming. The representing formula ofN(G,k) [J]. International Journal of Analyzing Methods of Combinatorial Biology in Mathematics, 2008, 1(1):1-26.

[10] 杨利民.S(n)-因子计数理论及其应用[D]. 大连:大连理工大学, 2006.

YANG Li-min. Counting theory ofS(n)-factors and applications [D]. Dalian: Dalian University of Technology, 2006. (in Chinese)

Explicit formula of Hosoya index of four leaf tree with its sequence

YANG Li-min*1, DUAN Li-yan1, WANG Tian-ming2

( 1.School of Mathematics and Computer, Dali University, Dali 671003, China；2.School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China )

To research into the laws of Hosoya index for four leaf tree, by means of analyzing method of components in graph theory, the explicit formula of Hosoya index of four leaf tree and its sequence are solved. For generaltleaf tree, by adopting the same method, the explicit formula of Hosoya index of correspondingtleaf tree and its sequence are obtained. A family of Fibonacci sequences whose initial values are not the same are discovered, which provides some scientific

for combinatorics and graph theory.

four leaf tree;tleaf tree;S(n)-factor; Fibonacci number; Hosoya index

2016-04-10；

2016-09-25．

大理大学高层次人才科研启动基金资助项目(KY0719203410).

杨利民*(1965-)，男，博士，教授，E-mail:yanglm65@aliyun.com.

1000-8608(2016)06-0657-05

O157.5

A

10.7511/dllgxb201606015