基于频率控制的多约束风电塔优化方法

程 耿 东， 徐 向 东， 刘 晓 峰

( 1.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024；2.北京金风科创风电设备有限公司， 北京 100176 )



基于频率控制的多约束风电塔优化方法

程 耿 东*1， 徐 向 东1， 刘 晓 峰2

( 1.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024；2.北京金风科创风电设备有限公司， 北京 100176 )

提出了基于频率控制的多约束单管型风电塔优化方法．塔架简化成悬臂梁结构，其横截面参数作为设计变量，以最小化材料体积为目标函数，按照将塔架设计成刚-刚或刚-柔或柔-柔不同类型的要求设定塔架的固有频率约束，采用专业软件Bladed计算风荷载，按照风电塔规范考虑强度、稳定性和疲劳等约束，这使得优化结构更符合实际设计．考虑到采用Bladed荷载计算工作量很大，整个优化过程分为几个阶段，在每个阶段的开始，以前一个阶段的优化设计作为初始设计，并重新计算结构荷载，在该阶段内于固定荷载下用移动渐近线法(MMA)求解优化问题改进设计，所需的固有频率、强度及疲劳约束灵敏度采用解析法获得．对一现有塔架进行优化以说明方法的有效性．根据塔架固有频率和风机工作转速之间的关系，发展了高风电塔的分类．在此基础上，结合提出的优化方法，可以帮助设计者判定在指定高度和机型下哪种类型塔架更合适，为塔架概念设计提供有价值的参考．

风电塔；优化设计；多约束

0 引 言

随着世界经济的快速发展，能源危机和环境污染问题日趋严峻，风能作为一种潜力巨大的清洁可再生能源，正面临前所未有的发展机遇．进入21世纪以来，风电产业以极快的速度发展．全球风能理事会于2016年2月公布的数据统计[1]显示，截至2015年，全球累计风电装机容量已达432.419 GW，这表明风电行业已成为新世纪极具活力的新能源产业．据估计，到2020年风能将占全球能源市场的5%[2]．在丹麦，超过20%的电能来自风力发电[3]．近十年，中国的风电产业和技术突飞猛进，2015年以30.5 GW的新增风电装机容量位居全球第一，占全球新增容量的48.4%[1]．为了获得更强更稳定的风能，不断提高风电塔的高度成为风电行业的共识．然而，随着高度的增加，一方面风电塔会变得更柔，在循环荷载下更容易发生共振和疲劳破坏，另一方面塔架的造价会大大提高．所以，高塔的设计优化非常有意义．

风电塔设计涉及结构力学、结构动力学和空气动力学等多学科．不少学者在风电塔设计优化方面做了研究．Negm等[4]对典型的圆筒式塔架以每段塔架的长度、半径以及壁厚为设计变量，考虑强度、最大位移、质量和避免共振等约束的情况下，提出并比较了最小质量、最大刚度、最大化刚度与质量比值、指定固有频率范围以及最大化固有频率等5种优化目标，得出以最大化固有频率为目标函数效果最好．Uys等[5]对一幢45 m高的加肋圆筒型钢塔进行了以最小化成本为目标的优化设计．其中以每段塔筒的厚度、环肋的尺寸和数量等为设计变量，依据材料费用及其制造成本构造目标函数，根据欧洲规范[6]计算沿塔的荷载，在考虑塔筒局部屈曲以及环肋屈曲的约束下进行优化．Yildirim等[7]依据ASCE[8]等设计规范计算设计地震荷载和风荷载，考虑强度、疲劳、屈曲和自然频率的约束，采用遗传算法，对某1.5 MW风机的钢塔进行了最轻化设计．Zwick等[9]针对某一完整高度的海上格构式风电塔提出了一种迭代优化方法，采用DNV-RP-C203[10]规范中提供的方法，分析在极限荷载状态和疲劳极限状态下结构上关键位置的应力，对其进行减重设计，体现了格构式轻量化设计的潜力．Nicholson等[11]对风电塔和基础组合系统提出了以最小化材料成本和塔顶位移最小为双目标的优化问题，采用多目标遗传算法等多种优化方法在Isight软件自动求解．Haghi等[12]也对塔架与基础组合系统进行了研究，提出了一种综合空气动力学、流体力学、结构力学和土力学等多学科的优化方法，他们用此方法对一现有的SWT-3.6-107海上风机的塔架和基础进行了优化设计，结果使支撑结构的整体质量减少了12.1%．

在这些研究中，优化过程使用的荷载虽然是根据规范计算，但往往只根据给定的一种风速并在整个优化过程中是固定的．但实际上，风荷载有很多工况并且是一个随机过程，塔架的荷载是与塔架的尺寸及动力性能有关的，在优化迭代过程中，随着结构的变化，荷载也会发生改变．为此本文提出基于频率控制的多约束风电塔优化方法．

1 多约束风电塔优化问题

1.1 优化列式

风力发电机系统很复杂，包括叶片、轮毂、机舱、发电机、塔架、基础等部分．本文中将塔架简化成非均匀的欧拉-伯努利梁，忽略塔内平台等非承重结构，塔顶结构(如风轮、机舱等)用集中质量代替．塔架坐标系如图1所示[13]，坐标原点位于塔架中轴与基础上表面的交点，整个坐标系不随机舱转动．本文提出优化问题是使风电塔具有指定的固有频率，并在满足强度、稳定性、疲劳以及横截面尺寸边界约束下，得到体积最小的设计．若将风电塔分成N个梁单元，则此问题的优化列式如下：

find X=(x1x2…xn)T

(1a)

(1b)

s.t.

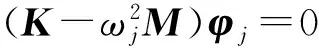
(1c)

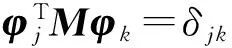
(1d)

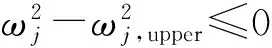
(1e)

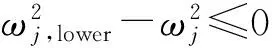
(1f)

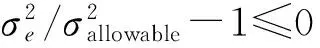
(1g)

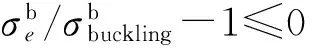
(1h)

D-1≤0

(1i)

Xlower≤X≤Xupper

(1j)

式中：X是设计变量向量，V是塔架体积，Ae和Le分别代表第e个单元的横截面面积和长度．ωj和φj分别表示塔架第j阶固有角频率和相应的特征向量．广义特征值问题(1c)中的K和M分别为对称的刚度阵和质量阵．式(1d)保证各相应的特征向量关于质量阵正交归一化．Xupper和Xlower分别为设计变量的上下限．约束条件(1c)～(1i)将在1.4节讨论．

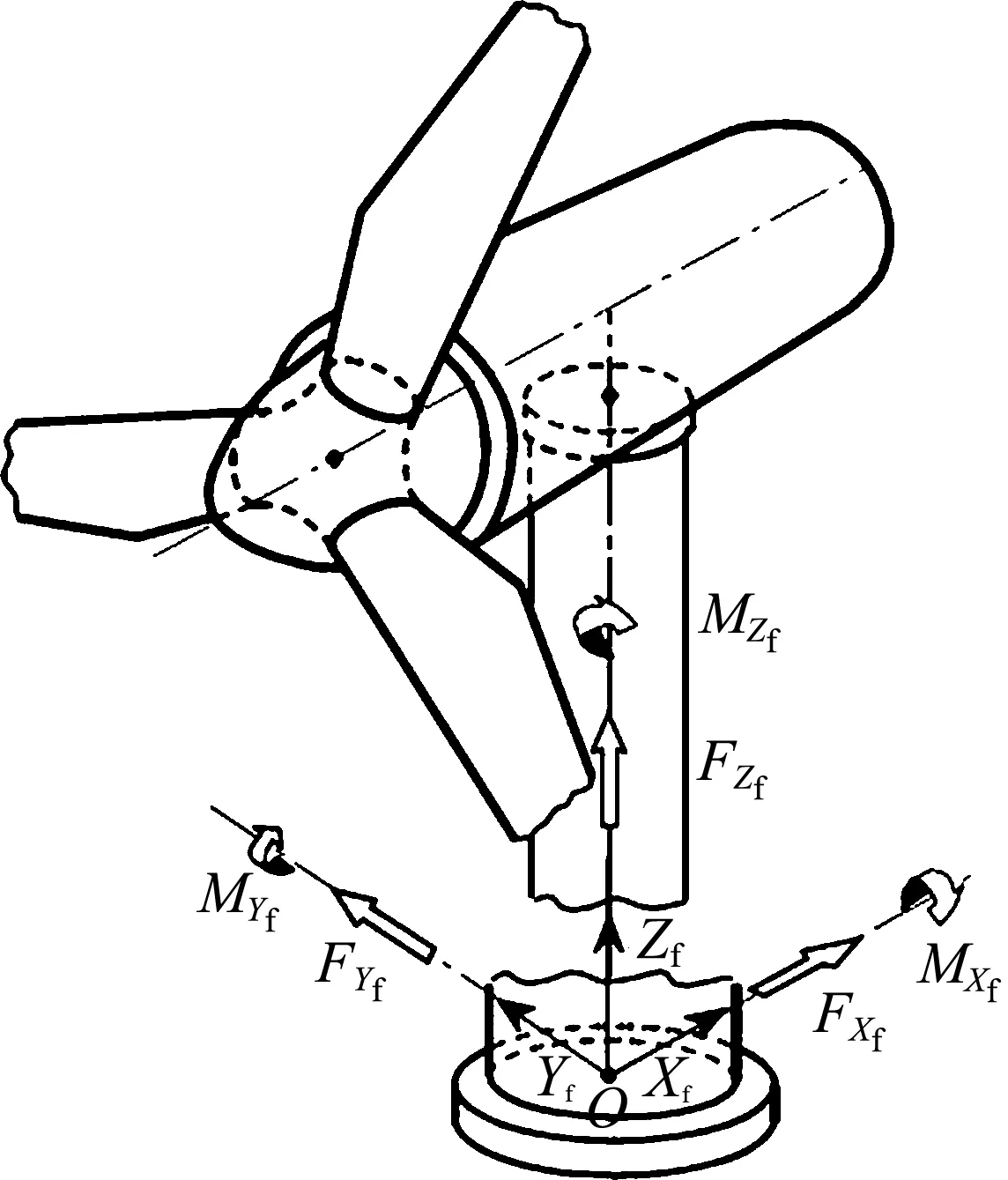
Xf水平；Zf沿塔架轴方向垂直向上；Yf水平，使Xf、Yf、Zf符合右手定则

图1 风电塔坐标系

Fig.1 Wind turbine tower coordinate system

1.2 风荷载计算

风荷载对风电塔优化设计非常重要，直接影响优化结果的有效性．在许多现有的文章中，风荷载简化成作用在塔顶的一个集中力和弯矩，或者是根据设计规范将风荷载看成是沿塔架高度方向的分布式荷载，但均未考虑振动的影响，而且只根据给定的一种风速并在整个优化过程中是固定的．实际上，风荷载的方向和风速是不断变化的，具有极强的随机性，因此专业设计时，需要考虑大量不同工况并模拟风的非平稳随机特性．此外，结构荷载会受到由于塔架与风机耦合振动引起的动力放大的影响，并且随着结构尺寸和频率的变化，其荷载也是有差异的．Bladed是一个计算整机荷载的专业软件，它通过建立正常湍流、极端风速、极限持续阵风、极端方向变化等多种风模型，考虑塔影效应、温度等因素的影响，对正常发电、启动、停机、故障等多种设计荷载工况计算风力发电机系统的内部荷载(塔架荷载、叶片荷载和轮毂荷载等)．

本文使用的荷载通过Bladed软件计算得到，考虑了700多个设计荷载工况，从中挑选出塔架的极限荷载，其中包括每个截面的剪力(Fx、Fy、Fz、Fxy)和弯矩(Mx、My、Mz、Mxy)，以及用于疲劳计算的64×64的Markov矩阵．矩阵中的每个元素分别表示64种均值荷载下64种不同幅值的循环次数．

1.3 设计变量

风电塔横截面参数作为设计变量X，依据不同的截面形状，如图2所示，定义相应的设计变量．例如，对于圆环形截面塔架，每个截面的外半径R=0.5D和厚度t作为设计变量；如果塔架截面形状为圆角正方形，直边的长度l、圆角的半径R和厚度t可作为设计变量；如果采用正六边形截面的设计方案，设计变量可以是边长l和厚度t．这些设计变量都需满足上下限约束，即Xlower≤X≤Xupper．

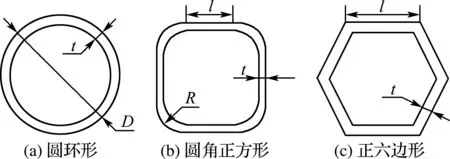
图2 不同截面形状的设计变量

本文选取圆环形截面塔架进行优化设计，其横截面面积A和惯性矩I可依据设计变量R和t写成

A=π(R2-(R-t)2)

(2)

(3)

根据每个截面的面积A、惯性矩I以及荷载，可以得到塔架的固有频率以及塔壳的强度、稳定性和疲劳等相关信息．

1.4 设计约束及灵敏度分析

1.4.1 塔架固有频率与相应的灵敏度分析 风电塔的固有频率会影响结构动力响应和外部风荷载，特别是一阶频率和二阶频率．当这些低阶频率落在风机工作转速范围时，结构荷载会大大增加，并且可能引发共振．因此，本文将塔架固有频率控制作为结构设计优化时最重要的约束，即列式(1e)、(1f)．

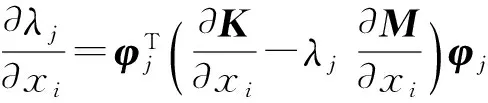
(4)

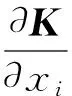
对于单特征值λj，若所有的设计变量同时变化，那么其线性增量Δλj为

Δλj=λjΔX

(5)

式中：ΔX=(Δx1Δx2… Δxn)T，为设计变量增量向量；λj是特征值λj关于设计变量的梯度向量，即

(6)

1.4.2 静强度 风电塔的静强度约束(1g)可以用第四强度理论来校核，即每个截面的等效应力应满足

(7)

式中：fy,k和fy,d分别为材料强度的标准值和设计值，γm为材料分项系数．等效应力σv可由以下公式求得：

(8)

其中A为截面面积，Wxy和Wt分别为抗弯截面系数和抗扭截面系数．若塔架横截面是以外半径R和厚度t为设计变量的圆环形截面，那么Wxy和Wt分别为

(9)

(10)

为了简化公式，去掉等效应力公式中的根号，则静强度约束条件可写为

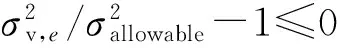
(11)

其中σallowable=fy,d为材料强度设计值，那么关于设计变量R和t的灵敏度易于求得，即

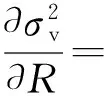
(12)

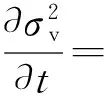
(13)

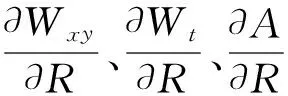
1.4.3 稳定性约束 对于稳定性约束(1h)，根据设计规范EN 1993-1-6-2007[16]，塔壳的正应力设计值σx,Ed和实际轴向失稳临界应力σx,Rd应满足

(14)

σx,Rd由以下公式计算：

(15)

这里，γm为材料分项系数，根据设计规范[13]取值．折减系数χx根据以下公式计算：

(16)

上式中的相关参数可查阅规范EN 1993-1-6-2007[16]计算．

由于以上计算塔架稳定性的解析公式过于复杂，虽然可以推导解析的灵敏度，但无论从编程还是计算量考虑，本文采用差分法计算稳定性关于设计变量的灵敏度．

1.4.4 疲劳 对于疲劳损伤约束(1i)，根据Palmgren-Miner累积损伤理论[17]以及材料的S-N曲线，钢塔的疲劳损伤按下面公式计算：

(17)

其中D表示损伤，当D>1 时，表示损伤破坏．本文中用于计算疲劳损伤的数据来源于Bladed软件计算得到的64×64的Markov矩阵(见1.2)，所以这里Nf=64．其他参数的意义如下：Δσe为应力变化幅值，这里仅考虑主要荷载My所产生的应力，即Δσe=ΔMy/Wy；ne为应力变化幅值Δσe对应的循环次数；m为材料S-N曲线的斜率；N0为材料S-N曲线上根据Δσe对应的循环次数；Δσ0为材料S-N曲线上根据Δσe对应的应力幅值．

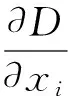
(18)

1.5 优化过程

风电塔优化设计问题(1)通过迭代求解，如图3所示．第一步，初始化设计变量xi，i=1,2,…,n，并指定材料、几何参数、有限元模型参数，以及约束条件参数．例如，按照将塔架设计成刚-刚或刚-柔或柔-柔不同类型的要求指定塔架固有频率上下限、强度和稳定性的临界应力，以及设计变量上下限等．整个优化过程包括3个循环，即荷载循环、外循序和内循环，如图3所示．

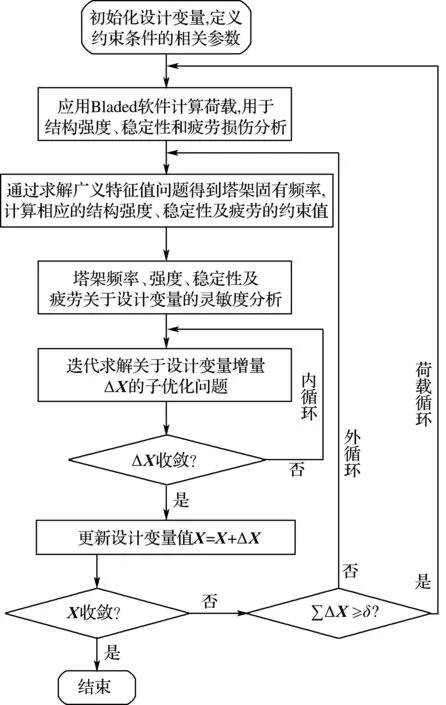
图3 迭代求解流程图

1.5.1 荷载循环 采用Bladed计算荷载是十分耗时的，所以仅当结构变化足够大时才应用Bladed 重新计算荷载．在优化过程中，首先应用Bladed计算初始设计的荷载，用于结构强度、稳定性及疲劳分析．然后，在随后的优化迭代过程中，结构荷载均保持不变．在每一次迭代结束后更新设计变量，即X=X+ΔX，并且检验是否需要重新计算荷载，其判定条件为在该荷载循环中先前所有迭代步设计变量变化的总和是否大于预先定义的值δ，即

sum ∑Δx1,…,∑Δxn≥δ

(19)

随着设计变量的不断更新，在没有收敛之前如果满足了判定条件(19)，那么需应用更新后的设计重新计算结构荷载，如图3所示．通过这种方法，整个优化过程被分成几个荷载循环，在每个荷载循环内使用固定的结构荷载．

1.5.2 外循环 如图3所示，外循环中的第一步是通过求解广义特征值问题(1c)得到塔架固有频率，以及依据前一迭代步更新的设计变量和荷载计算强度、稳定性和疲劳损伤．值得注意的是，由于这里并未出现重特征值的情况，故本文仅考虑特征值问题(1c)单特征值的情况，那么相应的特征向量φj,j=1,2,…,J也是唯一的．

外循环中的第二步，是计算塔架频率、强度、稳定性及疲劳对设计变量的灵敏度，具体方法见1.1～1.4节．外循环的第三步是一个求解子优化问题的内循环(如图3所示)，其中将用到这些灵敏度．

在外循环的第四步中，首先更新设计变量，即X=X+ΔX．然后检验设计变量是否收敛，若设计变量增量向量ΔX的范数小于预先给定的一个小量ε，则表示收敛，那么优化结束并得到最优设计塔架(如图3所示)．否则，更新后的设计变量作为下一个外循环的初始设计继续迭代优化．要注意的是，在开始下一个外循环开始前需检验是否需要重新计算结构荷载，见1.5.1节中介绍．

1.5.3 内循环 根据1.1～1.4节中塔架频率、强度、稳定性及疲劳关于设计变量的灵敏度分析，在外循环中建立一个内循环来求得最优的设计变量增量Δxi,i=1,2,…,n，即求解下面的子优化问题：

(20a)

(20c)

e=1,2,…,N

e=1,2,…,N

(20h)

xlower≤xi+Δxi≤xupper；i=1,2,…,n

(20i)

注意，在这个子优化问题中只有设计变量增量Δxi,i=1,2,…,n是待优化的．设计变量xi,i=1,2,…,n，塔架固有频率ωj,j=1,2，以及相应的灵敏度等在这个内循环中是不变的．本文采用移动渐近线法(MMA)[18]求解子优化问题(20)．

2 风电塔设计的分类

风电塔会长期受到风轮的转动引起的振动荷载，所以避免塔架在循环荷载下发生共振是非常必要的．但是，对于高塔，在风电系统启动过程中，通过采取适当的措施，包括主动控制，应该允许风机与结构发生短暂的共振．Hu等[19-20]对某97 m高的风电塔经过两年的检测发现存在这样的共振．这样的风电塔已经不是传统的刚性塔架．根据塔架固有频率与风机工作频率范围的关系，风电塔可以分成刚-刚、刚-柔、柔-柔等设计类型．为了更清晰地描述不同的塔架设计，本文给出一个风电塔设计的Campbell图(图4)．在图中，横坐标为风轮的转速，纵坐标表示塔架的频率，两条水平线分别代表风电塔的一阶和二阶频率，而两条斜线则分别表示风轮转速频率和叶片通过塔架的频率(对于三叶片风机等于3倍风轮转速频率)．定义符号fij(i=1,3;j=1,2)分别表示两条水平线和两条斜线的4个交点，如图4所示．它们表示第j阶塔架频率ωj和i倍风轮转速发生共振时对应的频率．例如，f31表示塔架第一阶频率ω1与3倍风轮转速发生共振时对应的频率．图中的Ωlower和Ωupper分别表示风轮工作转速的下限和上限．从图4中可以看出，fij(i=1,3;j=1,2)的值很容易得到，并且它们之间存在一些特定的关系，如下：

f11=ω1

(21)

(22)

f12=ω2

(23)

(24)

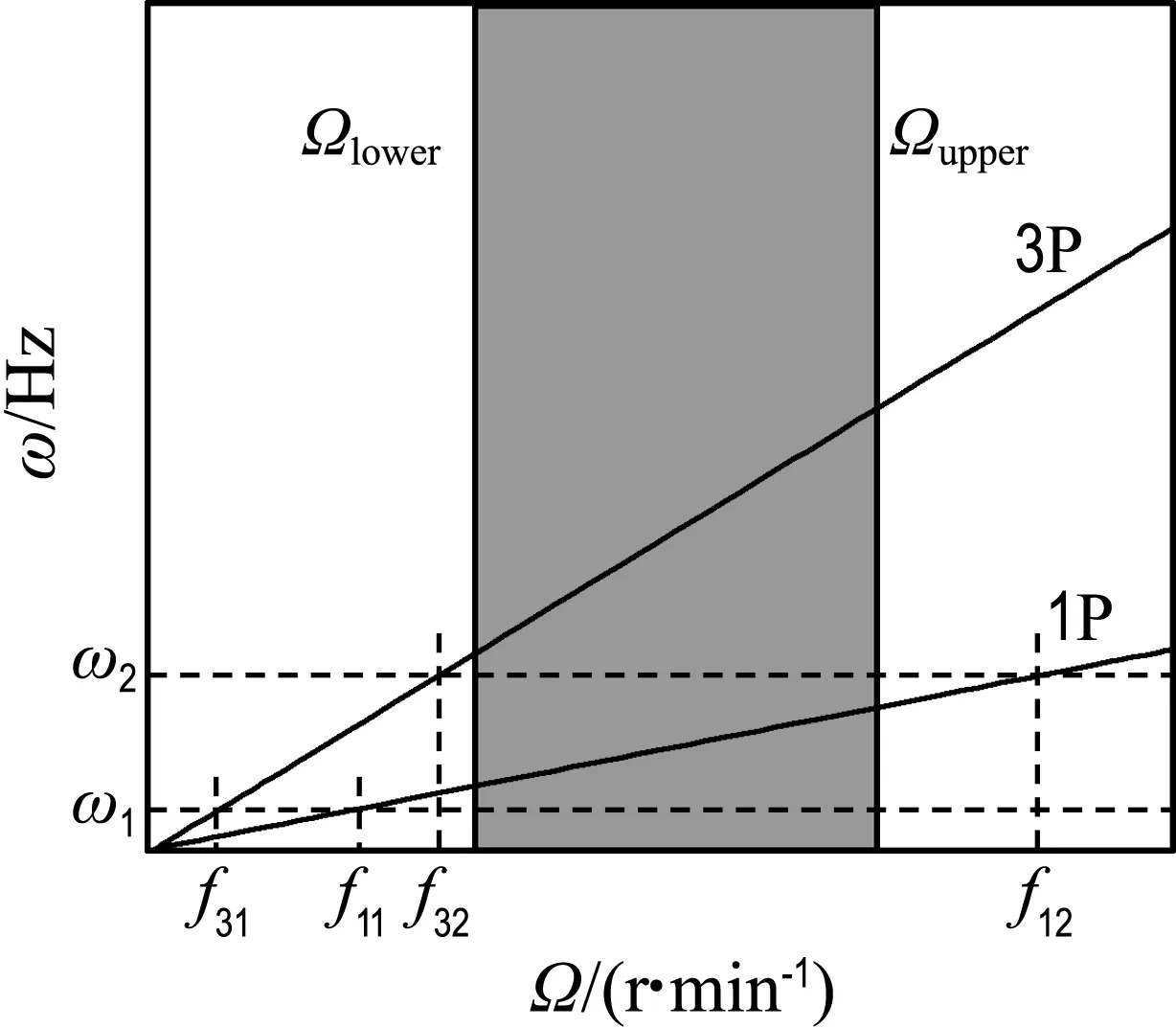
图4 风电塔设计Campbell图

若定义塔架的二阶频率与一阶频率之比为

(25)

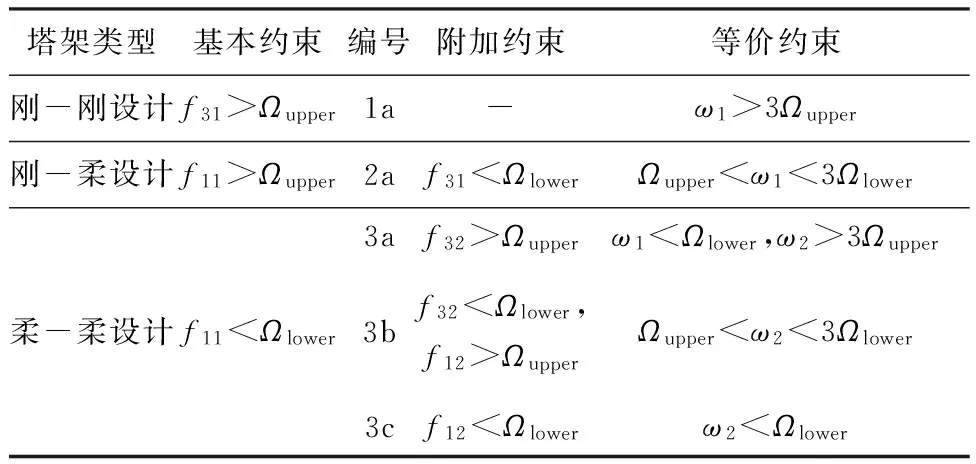
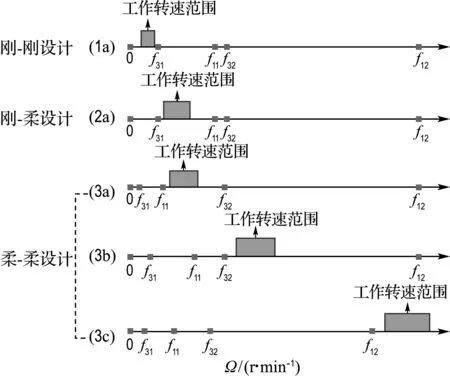
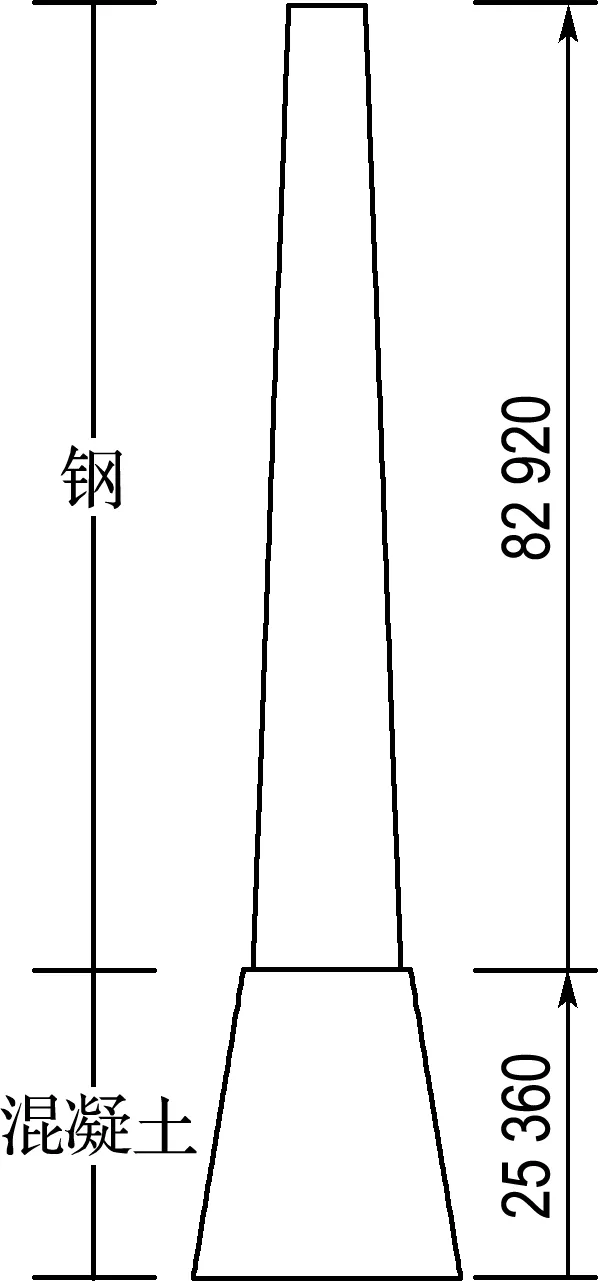
对于单管型塔架一般α>3，因此fij(i=1,3;j=1,2)之间存在固定的关系：

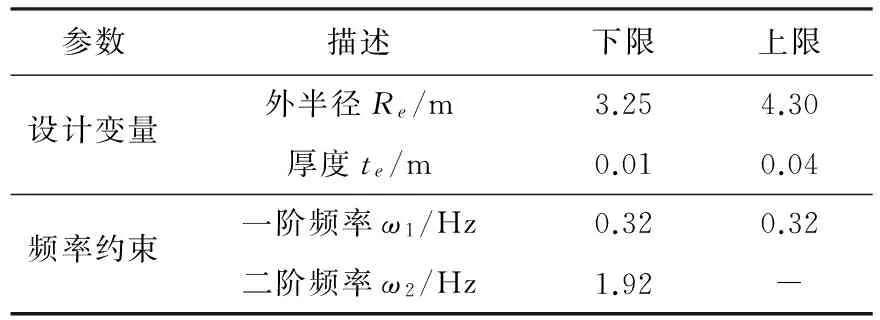
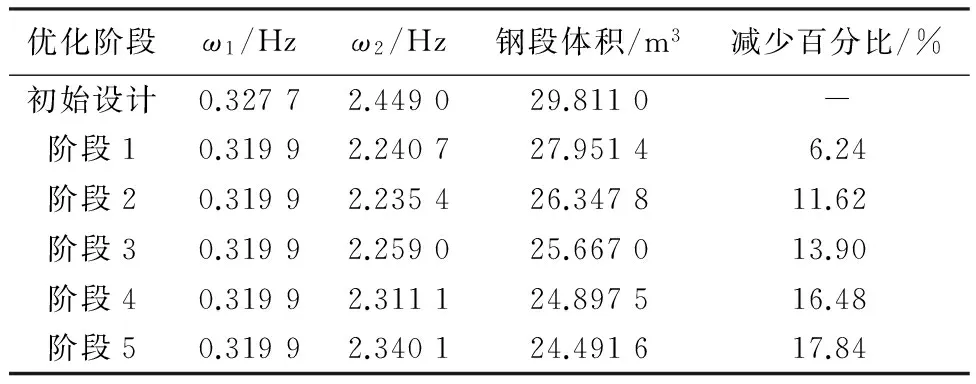
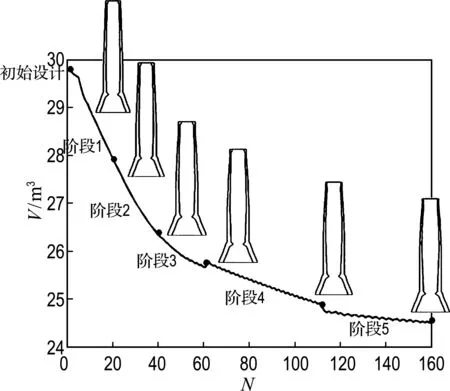
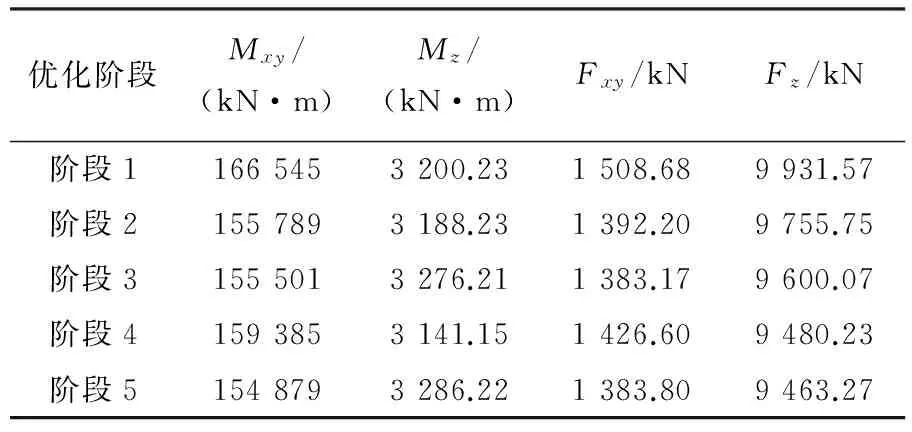
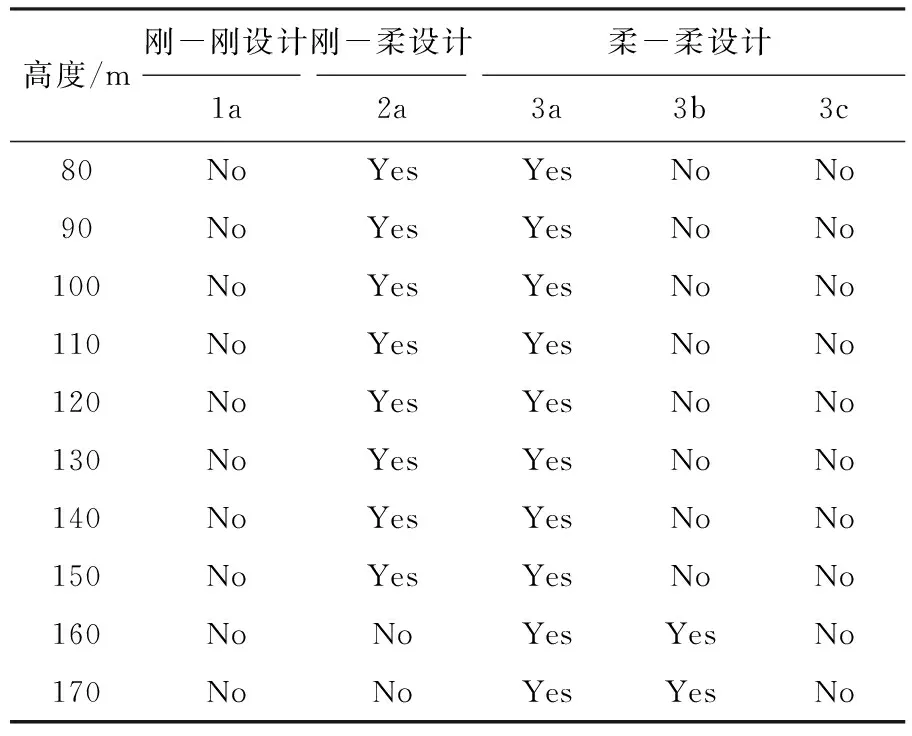
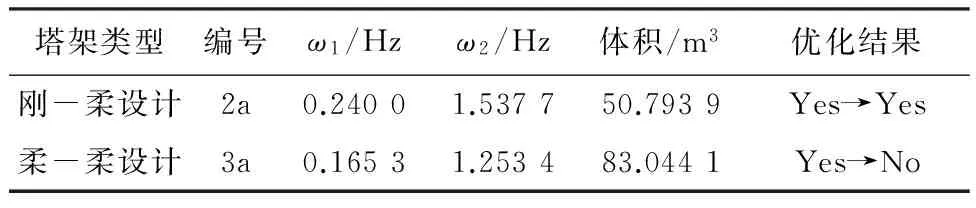
f31

(26)

依据上面的定义，可以清晰描述不同的塔架设计类型，如表1所示．为了避免共振，所有的交点fij都须落在风轮工作转速范围的外面．例如，刚-柔塔架设计意味着风轮的转速频率的上限小于塔架的基频ω1，叶片通过塔架的频率下限(对于三叶片风机等于3倍风轮转速频率)大于基频ω1，即基本的频率约束为

f11>Ωupper

(27)

同时次要约束为

f31<Ωlower

(28)

即表示频率点f31也不能位于风机工作转速范围之间，这一塔架在启动过程，风轮转速频率的3倍频可以和塔的基频发生共振，因此对叶频来说是一个柔性设计．其他的塔架设计均在表1中列出．图5中采用一维数轴图直观地表示了这些不同类型塔架设计．

但需要注意的是，2a和3b这两种设计只有当风机工作转速上下限满足以下关系时才出现：

3Ωlower>Ωupper

(29)

因此，在风电塔设计时，风轮转速范围是否满足条件(29)也是一个需要考虑的重要约束．

表1 不共振塔架设计

图5 不同塔架设计中fij和风机工作转速的关系

上述高风电塔分类方法更清晰地表达了不同类型的塔架设计的固有频率与风机工作转速之间的关系．结合本文提出的优化方法，能够说明在指定高度和机型下哪种类型塔架更合适，为塔架概念设计提供了有价值的参考．

3 数值算例

3.1 某2.5 MW风机塔架优化(算例1)

这个算例中采用的风电塔模型是参考某公司的钢-混组合塔架，如图6所示．塔高108.28 m，塔架下部为混凝土，上部为圆筒钢塔，两塔筒之间是刚性连接．钢和混凝土的材料参数见表2．整个塔架的横截面均为圆环形，所以设计变量为每个截面的外半径R和壁厚t，如图2(a)所示．

图6 塔架模型

表2 钢和混凝土的材料参数

本文将整个塔架简化为非均匀的欧拉-伯努利梁，共分成46个梁单元．塔架顶部安装的2.5 MW的风机看成一个集中质量加在梁的末端，塔顶风机的总质量为156 209 kg，包括3个叶片、机舱、发电机等．风力发电机的工作转速范围为7.5～13.5 r/min(即0.125～0.225 Hz)．

表3给出了优化设计时必要的参数，包括塔架一阶和二阶频率约束的上下限以及设计变量的边界．在这个算例中，目标函数为最小的钢材体积，并且指定塔架的一阶频率为0.32 Hz，二阶频率大于6倍一阶频率．需注意的是，本算例中只对塔架的圆筒钢塔部分进行优化，即塔架的混凝土部分的半径和壁厚在优化过程中是不变的．

表4列出了本算例的优化结果，包括每个优化阶段结束时塔架前两阶频率值、塔架钢段部分的体积以及钢段体积减少量相对初始设计的百分比．

表3 优化参数

从表4中可知，整个优化过程被分为5个阶段，钢段部分的初始体积为29.811 0 m3，而最后得到的优化设计的体积为24.491 6 m3，减少了17.84%．同时，塔架的一阶和二阶频率均满足了约束条件．图7中给出了钢塔体积优化迭代过程，并绘出了每一阶段结束时塔架模型的简单轮廓．

表4 优化设计结果

图7 钢塔体积优化迭代过程

另外，为了了解结构荷载在优化过程中的变化情况，提取出塔底(H=10 m)在每个优化阶段中的荷载数据，如表5所示．从表中可看出，所有的荷载分量在各个优化阶段都是不同的，特别是Mxy和Fxy，变化比较大．

表5 不同优化阶段中塔底的荷载(H=10 m)

3.2 不同高度下各类型塔架设计优化(算例2)

本算例结合上文中提出的高风电塔分类方法和塔架优化方法，对不同高度的塔架进行分类及优化，说明在指定高度和机型下哪种类型塔架更合适．在本算例中，所有候选塔架均为圆筒钢塔，所以以塔架每个截面的半径R和壁厚t作为设计变量．塔顶安装的风机型号与算例1中相同．考虑钢筒运输和制造的限制，设定半径允许的变化范围为1.625～2.150 m，壁厚允许的变化范围为0.01～0.10 m．

根据第2章中对塔架分类的讨论，由于此风机的工作转速范围为7.5～13.5 r/min，可以得到刚-刚设计、刚-柔设计和柔-柔设计的频率约束条件，见表6．

表6 不同塔架设计的频率约束条件

本算例分成两个步骤进行：第一步，对指定高度的风电塔仅考虑频率约束和设计变量边界约束进行优化，即通过优化列式(1a)～(1f)、(1j)先挑选出可能的优化设计；第二步，采用完整的优化列式(1)对可能的优化设计进行优化，检验是否能得到最优设计．

对80～170 m的10种不同高度的塔架进行第一步的优化，统计出各个高度塔架的各类设计是否满足频率约束的结果，见表7．其中，“Yes”表示该优化设计满足频率约束条件，“No”则表示不满足．从表中可以看出，对于某一特定的高度，不是所有的塔架类型都能满足频率约束的，而且随着高度的增加具有潜力可行设计趋向于柔性设计．

表7 不同高度塔架第一步优化统计结果

通过第一步挑选之后，排除了每种高度下不满足频率约束的设计类型．然后对每种高度下潜在的可行设计进行考虑全部约束的第二步优化．本算例中，只选择120 m高的塔架作为例子进行第二步优化．从表7中得知，120 m高的塔架只有刚-柔设计(2a)和柔-柔设计(3a)为潜在的可行设计，所以对这两种设计采用完整的优化列式(1)进行进一步的优化．计算结果如表8所示，经过第二步的优化后，可行设计只剩刚-柔设计(2a)，而柔-柔设计(3a)不能满足ω1<0.125 Hz的频率约束条件．同时，还得到了120 m高度下的刚-柔设计塔架的最优设计，其体积为50.793 9 m3，一阶和二阶固有频率分别为0.240 0 Hz和1.537 7 Hz．通过优化得到的最优设计可为风电塔设计初始阶段提供有一定价值的参考．

表8 120 m塔架第二步优化结果

4 结 语

本文提出了一种基于频率控制并要求满足多种几何和力学约束的单管型风电塔优化方法．在此方法中，单管型风电塔塔架简化成非均匀的欧拉-伯努利梁，整个塔架的材料可以是多样的．该优化方法对不同横截面形状的单管型风电塔均适用，例如，圆环形截面、正六边形截面等．从算例1中可以看到，在多种约束下塔架的材料体积得到了有效的减少，并且最优化设计的塔架具有指定的固有频率．

本文的优化方法有几个显著特点：首先，在设计优化时使用Bladed软件计算的结构荷载更符合实际，使得到的优化设计更具有实际意义．其次，该方法把塔架固有频率控制看成一个至关重要的约束条件．最后，本文采用基于梯度的优化算法求解该风电塔优化问题，并且除了稳定性约束的灵敏度是采用差分法计算外，其他约束条件及目标函数的灵敏度分析均采用解析的方法得到．

另外，本文还根据塔架固有频率和风机工作转速之间的关系，对高风电塔的分类进行了进一步的发展．结合本文提出的优化方法，可以发现在指定高度和机型下哪种类型塔架更合适，为塔架概念设计阶段提供有价值的参考．

[1] Global Wind Energy Council. Global wind statistics 2015 [EB/OL]. (2016-02-10) [2016-03-23]. http://www.gwec.net/wp-content/uploads/vip/GWEC-PRstats-2015_LR_corrected.pdf.

[2] JIN Xin, LI Lang, JU Wen-bin,etal. Multibody modeling of varying complexity for dynamic analysis of large-scale wind turbines [J]. Renewable Energy, 2016, 90:336-351.

[3] Hu Y, Baniotopoulos C, Yang J. Effect of internal stiffening rings and wall thickness on the structural response of steel wind turbine towers [J]. Engineering Structures, 2014, 81(81):148-161.

[4] Negm H M, Maalawi K Y. Structural design optimization of wind turbine towers [J]. Computers & Structures, 2000, 74(6):649-666.

[5] Uys P E, Farkas J, Jarmai K,etal. Optimisation of a steel tower for a wind turbine structure [J]. Engineering Structures, 2007, 29(7):1337-1342.

[6] Standard Policy and Strategy Committee Eurocode 1: Actions on Structures - Part 1-4: General Actions - Wind Actions: EN 1991-1-4-2005 [S]. London: British Standard Institute, 2005.

[7] Yildirim S, Özkol I. Wind turbine tower optimization under various requirements by using genetic algorithm [J]. Engineering, 2010, 2(8):641-647.

[8] American National Standards Institute. Minimum Design Loads for Buildings and Other Structures:ANSI/ASCE 7-88 [S]. Reston:ASCE, 2015:996.

[9] Zwick D, Muskulus M, Moe G. Iterative optimization approach for the design of full-height lattice towers for offshore wind turbines [J]. Energy Procedia, 2012, 24:297-304.

[10] Det Norske Veritas. Fatigue Design of Offshore Steel Structures, Recommended Practice: DNV-RP-C203 [S]. Norway:Det Norske Veritas, 2008.

[11] Nicholson J C, Arora J S, Goyal D,etal. Multi-objective structural optimization of wind turbine tower and foundation systems using Isight:a process automation and design exploration software [C] // 10th World Congress on Structural and Multidisciplinary Optimization. Orlando:WCSMO, 2013.

[12] Haghi R, Ashuri T, van der Valk P L C,etal. Integrated multidisciplinary constrained optimization of offshore support structures [J]. Journal of Physics:Conference Series, 2014, 555:012046.

[13] Germanischer Lloyd WindEnergie GmbH. Guideline for the Certification of Wind Turbines Edition 2010 [Z]. Hamburg:Germanischer Lloyd WindEnergie GmbH, 2010.

[14] DU Jian-bin, Olhoff N. Topological design of freely vibrating continuum structures for maximum values of simple and multiple eigenfrequencies and frequency gaps [J]. Structural and Multidisciplinary Optimization, 2007, 34(2):91-110.

[15] 徐赵东,马乐为. 结构动力学[M]. 北京:科学出版社, 2007．

XU Zhao-dong, MA Le-wei. Structural Dynamics [M]. Beijing:Science Press, 2007. (in Chinese)

[16] European Committee for Standardization. Eurocode 3:Design of Steel Structures, Part 1-6:Strength and Stability of Shell Structures:EN 1993-1-6-2007 [S]. Brussels:CEN, 2007.

[17] Miner M A. Cumulative damage in fatigue [J]. Journal of Applied Mechanics, 1945, 12(3):159-164.

[18] Svanberg K. The method of moving asymptotes-a new method for structural optimization [J]. International Journal for Numerical Methods in Engineering, 1987, 24(2):359-373.

[19] HU Wei-hua, Thöns S, Rohrmann R G,etal. Vibration-based structural health monitoring of a wind turbine system Part I:Resonance phenomenon [J]. Engineering Structures, 2015, 89:260-272.

[20] HU Wei-hua, Thöns S, Rohrmann R G,etal. Vibration-based structural health monitoring of a wind turbine system Part II:Environmental/operational effects on dynamic properties [J]. Engineering Structures, 2015, 89:273-290.

Frequency-based optimization method for wind turbine tower under multiple constraints

CHENG Geng-dong*1, XU Xiang-dong1, LIU Xiao-feng2

( 1.State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology,Dalian 116024, China；2.Goldwind Science & Technology Company Limited, Beijing 100176, China )

A frequency-based optimization method for single tubular wind turbine tower under multiple constraints is proposed. The cross section parameters of tower are design variables, and minimizing the material volume of tower, which is considered as a cantilever structure is objective function. The natural frequencies of tower are constrained to ensure the tower being stiff-stiff or stiff-soft or soft-soft design. The wind loads are calculated by commercial software Bladed, and according to specification of wind turbine tower, the strength, stability and fatigue are included in constraints, these factors make the optimum structure conform to the practical design. Since the load evaluation by Bladed is very costly, the whole optimization process is broken into several stages. At the beginning of each stage optimization starts by using the previous optimum design as its initial design and the wind load of the initial tower design is recalculated. In each stage, optimization problem is solved by method of moving asymptotes (MMA) under the fixed wind load, and the sensitivities of the natural frequency, strength and fatigue constraints with respect to design variables are obtained by analytical method. A numerical example for improving the existing tower design demonstrates the optimization method. Furthermore, a classification of high wind turbine tower is developed based on the relationship between tower natural frequency and working frequency range of the wind turbine to be installed. By the above optimization method, it can help to decide that which type of the tower design is the potentially optimum candidate for specific height and turbine, and provide valuable suggestions for optimum design during concept design stage for wind turbine tower.

wind turbine tower; optimization design; multiple constraints

2016-04-06；

2016-09-20．

国家自然科学基金资助项目(11332004).

程耿东*(1941-)，男，教授，博士生导师，中国科学院院士，E-mail: chenggd@dlut.edu.cn；徐向东(1989-)，男，硕士生，E-mail:xuxiangdong@mail.dlut.edu.cn.

1000-8608(2016)06-0551-10

TU359；TK83

A

10.7511/dllgxb201606001