四色图论——四色问题解的存在性及求解方法

杨 名 生

( 大连理工大学 工程力学研究所, 辽宁 大连 116024 )



四色图论
——四色问题解的存在性及求解方法

杨 名 生*

( 大连理工大学 工程力学研究所, 辽宁 大连 116024 )

直接从四色问题出发，建立图论的另外一个新体系．在提出区域、边界线、结点等定义，对复杂地图进行分层简化后，得到体系的3个基本定理，又用链路这一工具，证明任意有限个区域地图的四色解存在并给出了求解方法．

图论；四色问题；区域；边界线；结点；链路

0 引 言

图论起源于Könisberg七桥问题和Guthrie的四色猜测．Euler图给出前者一个否定的结果，并推动图论的发展，建立了图论的传统体系．它从确定事物的点(称为顶点)出发，通过两点间连线(称为边)的集合构成线状图(有向图或无向图，平面图或非平面图)，并用矩阵工具对路径、回路、信号流图等规律进行研究．同时也推动了四色问题的研究[1-2]．20世纪70年代，Appel和Haken用当时的电子计算机经过近千小时的运算证明四色问题[3-4]，直到80年代才得到学者的首肯，原因是其几百页的逻辑推理公式太繁杂，数学界更期待有简捷的常规证明[4-5]．

四色问题可简述如下：任何平面地图都可用4种颜色着色，使其相邻区域着色不同[1]．

引导图论诞生的四色问题，具有不同于七桥问题的特点，它关心的是区域的相邻性．区域有很大的任意性，本文提出一系列简化处理方案并引入链路等新概念，将求解四色问题简化为求基础地图的四色解，并最终解决四色猜测问题．

1 预备知识[6]

1.1 约定和定义

1.1.1 地图 地图是球面的一种划分，它使球面的某些点只属于1个区域，某些点属于2个区域，某些点属于3个或3个以上区域．不存在不属于任何区域的点；区域都是R2的二维空间的一片[7]，不关心区域形状和面积大小，它必须是二维的，不能是一维的线或零维的点，换言之，不存在只有有限个点或R1个点的区域．

为表示地图而把球面剖开展平画在一个矩形平面上，此时剖线展为矩形，周边不具有任何几何意义．矩形平面全体与球面全体完全对应，这是一个最简单的、无任何边界线和结点的单区域地图；若球面地图有复杂的边界线和结点，则剖线一定不能与任何边界线相交，也不能过任何结点．

1.1.2 区域、边界线和结点 区域是若干条边界线所围成平面中的有限部分，区域的分割取决于边界线，边界线是一维的，属于R1[7]．边界线两侧分属于两个不同区域，只有边界线为它所分割的两个区域所共有，边界线之外的点必属于且仅属于一个区域．一般边界线(Jordan曲线)分割两个区域并为它们所共有，不关心其形状和长度；边界线的两个特殊点为3个或3个以上区域所共有，这种点称为边界线的结点，它没有形状与大小，是划分两个区域边界线的端点(起点或终点)，是不同边界线的交接点(这里不讨论只有一个结点和没有结点的边界线)；结点的阶是交于此的边界线数，用J表示，它也是共有该点的区域个数，显然有J≥3，结点的阶为3时特别称为简单结点；区域的边界线可细分为内边界线和外边界线两种，也可以没有内边界线．区域内边界线若存在则表示区域内挖了孔洞，且不破坏区域的连通性，内外边界线的划分并没有绝对标准，在球面上它们都是自身不相交、又互相不相交的封闭曲线，当球面展开成为平面时(注意：剖线段不能与任何边界线相交)，从矩形周边向区域行进中首次遇到的是外边界线，之后遇到的是内边界线，故内外边界线的确定与剖线的位置有关．在区域拓扑关系分类中，只考虑区域的外边界线往往是很方便的，因为一个区域的内边界线必定是另外一个区域或一个区域集团的外边界线．

四色问题不关心区域的形状和面积大小，不关心边界线的形状和长短，不关心结点的具体位置，只关心区域之间的相邻关系、结点间的边界线连接关系等．

区域是连通的，是指区域的任何两点都可以用区域的点连接起来；区域是单层的，是指区域的任何封闭曲线都可以在区域内收缩为一点，有内边界线的区域不是单层．

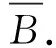
定理1(互换定理) 若地图的一种着色方案满足四色问题的要求，对换四色中任意两种颜色，得到的新着色方案依然满足四色问题的要求．

证明 在满足四色问题要求的一种着色方案中，任意取两个相邻区域，则它们的着色必定相异．如果对换的两种颜色与这两个区域的着色完全相同或者完全不同，则它们显然保持相异的特性；否则对换的两种颜色之一必与这两个区域着色之一相同，且对换的两种颜色的另外一种与两个区域中另外一个区域的着色不同．故对换后仍能保持两个区域着色的相异性．由于那两个区域是任意的，从而证明了定理．

推论1 地图满足四色问题要求的着色方案，分别可以指定某一区域的着色、指定相邻两区域的着色、指定彼此相邻三区域的着色．

据此，地图有一种满足四色问题的着色方案，必然有许多种不同的着色方案．为此可将解空间写成C={1c，2c，3c，4c}，其中的符号，例如1c可以代表B，也可以代表G、R或Y，不同符号代表不同着色．凡是通过对换可以互相转化的两种着色方案称为同一类解；如果地图只有一类解，则称其解是唯一的．

1.1.4 原始图与生成图 地图的所有区域都是单层的，且所有结点都是简单结点，则称其为原始图；当至少有一个结点不是简单的则称其为生成图．原始图的某条边界线的长度缩减为零时，重合结点的阶上升为4，此新图为原始图的生成图．两图相比区域数相同，原始图的结点数和边界线数都最多，即相邻关系最多，故原始图的四色解也一定是其生成图的四色解．生成图和原始图的互化方法并不唯一．假设原始图的边界线数为b，简单结点的个数为n，则有b=3n/2．此式说明n必为偶数，引入图的特征数m，令n=2m，则b=3m．

1.2 几个定理

定理2(基本定理1) 设原始图中区域数为r，结点数为n，边界线数为b，当r≥3时，如下关系成立：n(r)=2(r-2)，b(r)=3(r-2)．

证明 用数学归纳法证明此定理：

(1)当r=3时，由于是原始图，结点都是简单的(见图1)，应有r=3，n=2，b=3，结论显然成立．

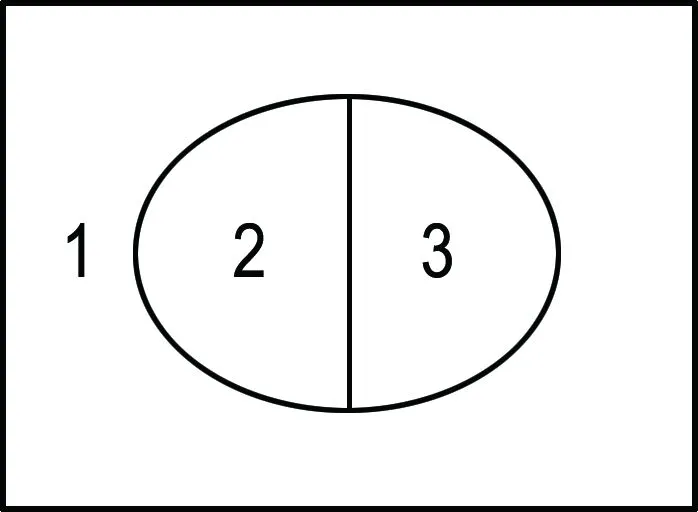
图1 r=3时的地图

(2)假定r=k时结论成立，有n=2(k-2)，b=3(k-2)．保持原始图的区域数增一的方法很多种，但都新增2个结点和3条边界线；有时区域的生成不止一个，此情况可以化为逐次增加一区域来组合实现[6]．这就证明结论对r=k+1亦成立．

基本定理1的结论与前文的分析是一致的，且更深入地揭示了原始图中的区域、结点和边界线三者之间的数量关系，引入图的特征数m=r-2．

推论2 单层图的区域数为r，结点数为n，边界线数为b，当r≥3时，有n(r)=2(r-2)-D，b(r)=3(r-2)-D，其中D是所有结点的阶减3的总和．显然有n-b+r=2，这正是图论中的Euler 公式[2]．

定理3(装配定理) 1个(图2(a)中A)、2个(图2(b)中A与B)或3个(图2(c)中A、B与C)相互相邻的区域如图2左边分割的两个区域集团G1和G2整体图四色问题，可以分解为图2中间和右边两个独立的子四色问题；如果这两个子四色问题都有解，则它们装配成的原四色问题(图2左边)也一定有解．

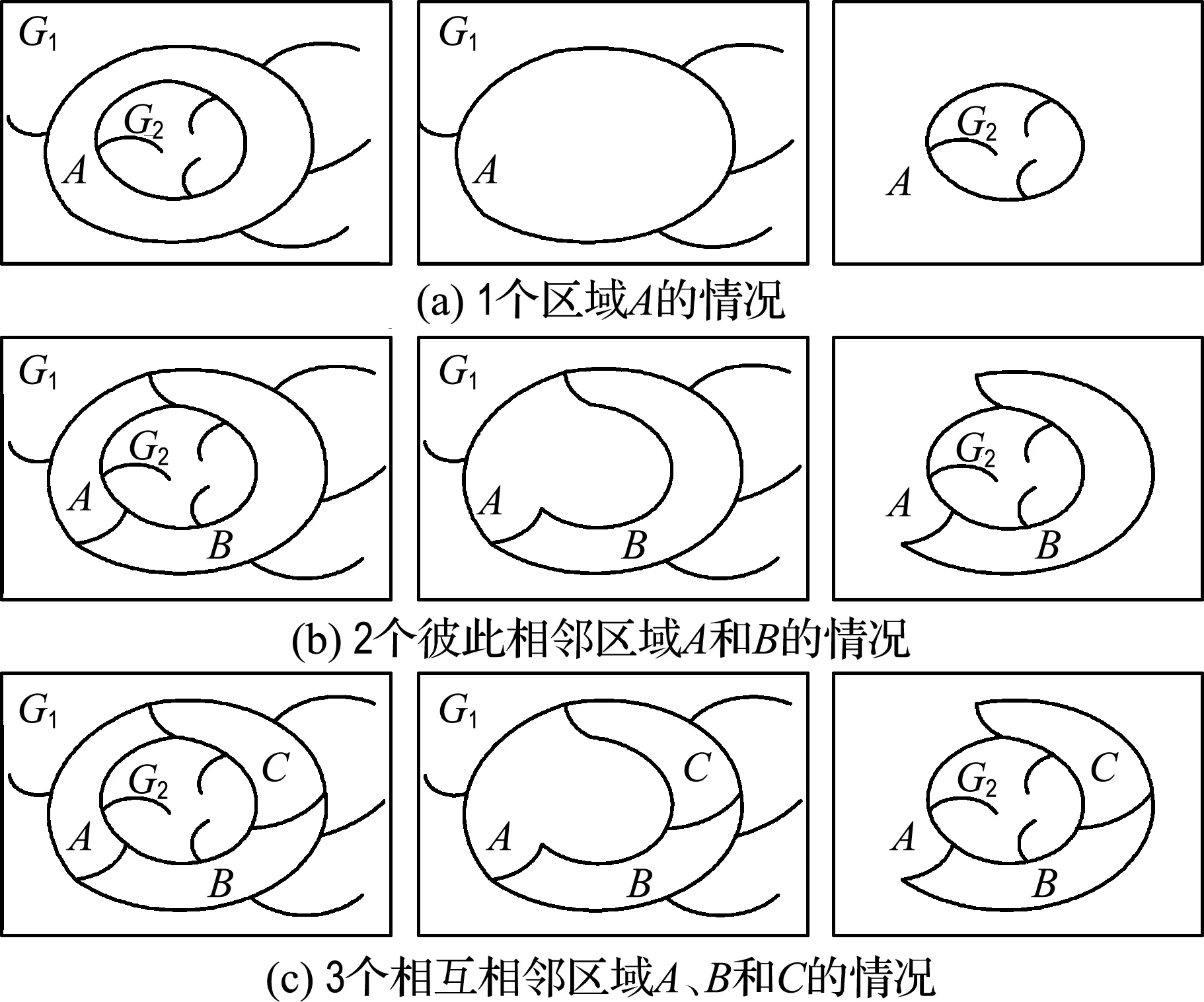
图2 化为相应子地图的复杂地图求解

证明 推论1给出证明．

图2(a)可称为第一类可移去问题(解决去孔洞)；图2(b)称为第二类可移去问题(解决去多次相邻)，特别当区域集团G1或G2为单区域时依然成立．装配定理解决了地图化为若干个无孔洞且相邻次数不多于1的子问题，从而使问题简化．

定理4(吸收定理) 对单层地图的二边、三边及四边区域，可将其吸收使图中区域的最小边界线数大于等于5．

这里所谓吸收系指彼此相邻的几个区域合并的操作．两个区域的合并使其相邻边界线消失，随之两条边界线也合并，总体减3条边界线及2个结点．

(1)吸收二边区域．二边区域的相邻两个区域二次相邻．实际处理时可被其相邻一区域吸收，使区域总数减一且那两个区域恢复一次相邻，地图返回解的二边区域着色不唯一，其两种选择都能满足特定要求．

(2)吸收三边区域．三边区域与周围彼此相邻的3个区域都相邻，被任一区域吸收时区域总数减一；地图返回解中，三边区域选取与那3个区域着色都不同即可．

(3)吸收四边区域．四边区域周围相邻的4个区域都彼此顺序相邻，但不存在相对的两个区域相邻．将四边区域与任何一对相对区域合并，地图区域数减少2；地图返回解中，若另一对相对区域的着色不同，四边区域取与它们都不同的第四种颜色；若另一对相对区域的着色相同，四边区域将有另外两种颜色可选择．

单层地图的所有结点都是简单结点，所有相邻都是一次相邻的问题称为简单问题．

定理5(相邻定理)r个区域简单问题，其相邻关系矩阵中非元总数：

j(r)=6(r-2)；r≥3

证明 由基本定理1和简单问题的规定可证明．

引入相邻关系矩阵的空元总数函数，记为v(r)，在简单问题中显然有

v(r)=r2-7r+12；r≥3

方程v(r)=0有两个根：r=3与r=4．v′(r)=2r-7；当r≥4时，v′(r)>0，故v(r)除去r=3和r=4两个零点外，再也没有零点．

特别是v(r)r21(r∞)，故有

推论3r个区域简单问题的相邻关系矩阵中空元总数：v(r)=r2-7r+12，其中r≥3．

推论4 简单问题中区域数很大时，其相邻关系矩阵为稀疏阵，即实元和非元总数随区域数增加而比例减少．

推论5 区域数相同时，简单问题的相邻关系矩阵的非元总数最多(或空元总数最少)．

定理6(基本定理2)r个区域的简单问题，其区域最小边界线数Bmin(r)取值只有3种可能：当4≤r<6时，只能为3；当6≤r<12及r=13时，可能为3，否则为4；当r=12及r>13时，可能为3，否则为4，若不然必为5，没有其他可能．

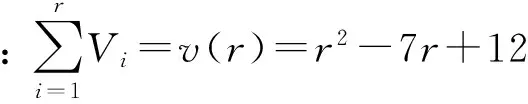
推论6 五色定理[2-3]是成立的．

证明 边界线数为5的区域与其周围彼此不相邻的任意两个区域合并，再求解生成的问题，这4个区域最多可着四色，如果有第五种颜色，则返回解必然存在．

r个区域地图的区域最小边界线数大于等于5表示为Bmin(r)=5，满足Bmin(r)=5的简单地图称为基础地图．

引用符号Bm，表示边界线数是m的一个区域．

定理7(基本定理3) 基础地图的B5个数在12的基础上，每出现一个Bm(m≥6)，B5个数都要增加m-6．

证明 当地图所有区域都是B5时，显然它的区域数必为12(见图3)．对于一般的基础地图而言，根据基本定理1知每增加一个单元，就会增加3条边和2个结点．如果这个单元是Bm(m≥6)，就其本身增加m个结点和m条边，超出基本定理1的要求，必须用x个B5来抵消；它们产生5x个结点和5x条边，总图增加1+x个单元，就单元而言增加m+5x条边，相当于总图增加(m+5x)/2条边，它应当是3(1+x)，即(m+5x)/2=3(1+x)，解得x=m-6，证明了此定理．

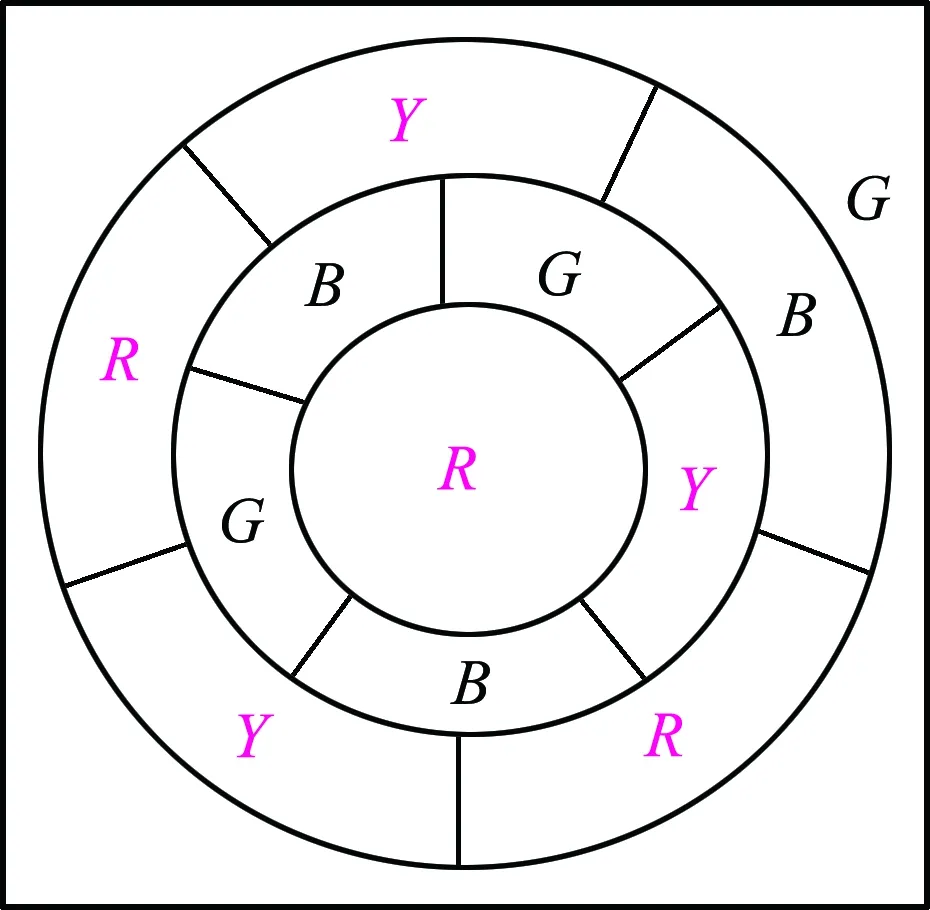
图3 r=12时的地图

2 链 路

2.1 链路的规定

基础地图的四色解系指，它的每个区域都从四色空间中着一色，且相邻区域着色相异．四色空间任意两种颜色可组成一条链路族，余下两种颜色则构成另外的链路族；彼此相邻且着色属于同一族的区域串接起来就构成了地图的链路，它的宽度是一个区域，每个区域又可称为链路的一个点(或单元)．满足四色解的基础地图的每个区域，都着一定颜色，也必定属于一个且仅属于一个链路族．

在C={1c，2c，3c，4c}约定下，考虑互换定理，不失一般性地认定{1c，4c}组成链路一族；{2c，3c}则构成链路另外一族．链路族组成方式有3种：{1c，4c}、{1c，2c}和{1c，3c}，相应地另外一族是{2c，3c}、{3c，4c}和{2c，4c}，显然链路中的两色应当顺序交错出现．

地图简单结点周围的3个区域，由于两两相邻使其在四色空间中着三色，故必有两个区域位于同一族，第三区域将属于另外一族，同族两区域的相邻边界线是链路的连接线，称为族相邻边界线(在不混淆情况下简称为“节”)；另外的两条边界线则为两族间链路的分界线(或简称“边”)．

链路的点有以下几种类型．(1)孤立点：与它相邻的周围区域都是另外一族，这些区域构成该族的封闭环，因而这些区域的个数必为偶数，故孤立点的区域边界线数也是同样的偶数．(2)端点：与它相邻的周围区域有且仅有一个区域和它同族，这个区域成为一条链路的起止点，余下区域则构成另外一族的开口环．(3)过点：与它相邻的周围区域有且仅有两个彼此不相邻的区域和它同族，它成为链路的中间点．(4)分支点：与它相邻的周围区域有3个或3个以上彼此不相邻的区域和它同族，它成为一条链路的分岔．一条链路(或环路)只有通过分支点才能连接多条同族链路，按规定显然分支点的边界线数应大于等于6．

B5点只能做端点和过点，不能做孤立点和分支点；对于Bm点：当m≥6时，可做端点、过点和分支点，当m为偶数时，还可以做孤立点．

2.2 链路的基本要求

链路是四色解的产物，它的两条基本要求也就是四色解的要求：(1)链路中顺序各点着色必须是族中指定两色交替出现，特殊情况可能是族中指定两色之一(例如孤立点)．(2)链路仅在分支点处能连接同族链路，其他情况同族链路不能相邻，它们之间必为另外一族所隔离．这是分支点的边界线数应大于等于6的原因．

2.3 链路的几种类型

若干依次相邻的同族区域构成的链路有几种类型．(1)无分支链路：由同族的两个端点和中间若干过点依次相邻组成，链路端点位于另外一族的开口环内．链路的长度系指其区域个数，当长度为1时，它没有过点且两个端点重合为一点(孤立点)，其周围是另外一族的封闭环．(2)无分支封闭环链路(简称环路)：当无分支链路的长度为大于等于6的偶数，且两个端点相邻而使端点消失时，则形成一族无分支的封闭环路，其每个点都是过点，并将另外一族分隔为没有联系的两部分，使它们可以各自独立地交换双色；每个关联部分特称为独联体，从而增加了交换色的灵活性．(3)链路或环路带分支的链路：它的特点是某些过点同时也是分支点，通过这些分支点可以连接若干个同族的分支链路，当然分支还可以再带分支，多一个分支则多一个端点．分支链路将随同主链路一起变换着色．环路带分支链路时，其边长度为环路长度与分支链路长度的2倍之和(它当然是偶数)，它等于所围另外一族的区域集团的和区域边界线总数[6]．分支使链路千变万化，能适应各种复杂的区域随机分布．(4)同族的封闭环链路之间直接连成一体，或通过链路间接连成一体，都是通过某些既是过点又是分支点而完成的，它们要一体地赋值．封闭环链路内部或外部的异族可各自独立地赋值或交换．

2.4 链路的多样性及产生多个四色解

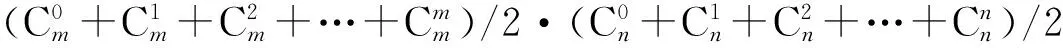
若是再改变链路定义，着色方案虽然不变，却可能产生一些新链路而形成新独联体，独联体的单独或联合变换，虽然不改变链路形状，但确实改变了着色方案，……由此可见，想通过已确定的千变万化的区域布局，来逻辑地推出四色解是不现实的，因为存在的解可能非常多．下面用12块五边形和20块六边形区域构造的老式足球为例说明．

图4是32个区域组成的老式足球图，这3个图的着色其实完全相同，但它们的链路规定不同，因而独联体的个数也不同．图4(a)I=2(1+1)图的族构造是R-G、B-Y，独联体数为1+1，它只有一个四色解；图4(b)I=4(2+2)图的族构造是R-B、G-Y，独联体数为2+2，它将有4个不同的四色解；图4(c)I=6(2+4)图的族构造是R-Y、B-G，独联体数为2+4，它将有16个不同的四色解．

图5同样是32个区域组成的足球图，它们的链路规定完全相同，都是R-Y、B-G．图5(a)的独联体数为1+2，它将有2个不同解．对换B与Y后，再将孤立点的G换成B而成图(b)，它的独联体数为2+3，它将有8个不同解．将图(b)的B与Y对换而成图(c)，它的独联体数为1+6，它将有32个不同的四色解．

综上所述，改变链路族的结构、交换部分独联体双色、两种操作组合进行，都能带来环状结构的大量新四色解．就上述足球而言至少有32种不同的四色解．

2.5 链路定理

定理8(链路定理) 基础地图的四色解中，链路图的任何结点都仅连一条族相邻边(简称为节)和两条族间边界线(简称边)．

证明 从略．

对于满足四色问题要求的基础地图的链路图而言，链路定理指明：(1)节绝不相互连接，不管是同族还是异族．(2)边依次连接形成封闭一笔画线．(3)一条节的两端分别支撑两条边，节将同族的两个区域连接，边将不同族分隔开．链路定理对一个结点而言是解的必要条件，对一批结点(或所有结点)就变成四色解的充分条件，封闭一笔画边线的延续性使四色解的存在性得到证明，还提供了求四色解的操作方法．基础地图划分区域的边界线，此时分为节和边两大类．

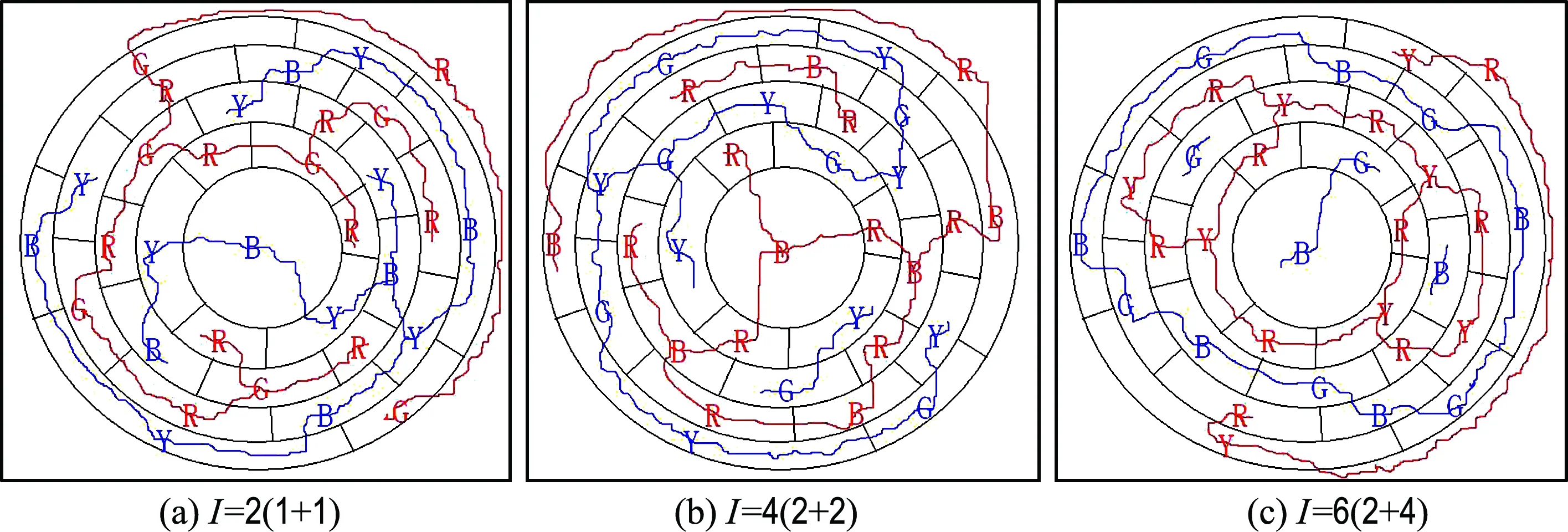
图4 老式足球(12B5+20B6)的3种链路图

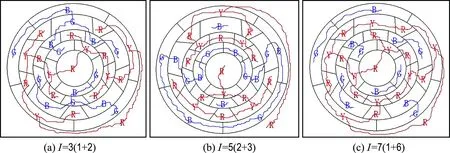
图5 老式足球(12B5+20B6)的另外3种链路图

2.6 基础地图的链路形式决定区域和节的数量关系

链路定理表明全图的区域数比节数多2．不同的链路形式确定不同的区域数与节数之间关系：(1)无分支链路族的区域数比节数多1，对于孤立点也是如此．(2)无分支封闭环链路族的区域数和节数相同．(3)链路或环路所带分支链路的区域数和节数也相同，包括分支又带分支的情况．(4)同族链路或同族环路(及其分支)相遇会使族的区域数比节数减少1．

2.7 基础地图解的存在性

r个区域的基础地图，根据基本定理1可知，其结点数n(r)=2(r-2)，边界线数b(r)=3(r-2)．按链路定理原则可知，要有r-2个节和2(r-2)条边，且这些节没有任何两个相连接，这些边依次顺序相连，成为一个或若干个一笔画的封闭线．上述结点数和边界线数恰能满足链路定理的要求．

当链路无环形结构时，即I=2(1+1)情况，基础地图的边将全空间分成互不联系的两部分，各为链路的一族；由2.6可知每一族的区域数比节数多1．要特别指出的是，这里的一笔画线严格受控于节，每一笔画线都由节支撑其宽度，或者说由节来连接同族的两个区域．首先指出最简单的基础地图是12B5，它有四色解(见图3(a)和图6(a))；r>13的首个2B6+12B5也有四色解(见图6(b)，红蓝都是无分支的链路，其边为一笔画的封闭线)，在此基础上逐一增加区域，考察一笔画图形应当如何变化．同族链路增加一个区域只有3种方式：(1)链路的端点增加一区域(见图6(c)上部黑虚线，生成五边区域)；(2)链路的过点增加一区域(见图6(c)下部黑虚线，对其上生成七边区域)；(3)链路的过点生出新的分支链路(见图6(d)右部黑虚线，对其右生成六边区域)．

图6(c)、(d)中黑实线表示红与蓝两族的边，红、蓝虚线分别表示红、蓝族的节，黑虚线表示为增加一区域引进的新节，它连接新引进的两个结点，另外两条边则保持一笔画的线路；如同基本定理1所指出的那样，区域增一使全图增加2个结点和3条边界线，结果是或者使链路长度增一，或者使它生出新分支链路．一笔画的封闭线路，形成红族和蓝族各自的树状结构，用梳齿型结构来描述更为恰当；每一条无分支的链路都相当一个齿，这些不同颜色的齿交错分布，每个齿都有一个端点，同族齿在分支点处相连成为一个整体，它的外廓就是红蓝两族的分界线，就是边连成的封闭一笔画线，构成该基础地图的I=2(1+1)的四色解，类似于图4(a)中的I=2(1+1)结构的四色解(红5齿对蓝4齿)．

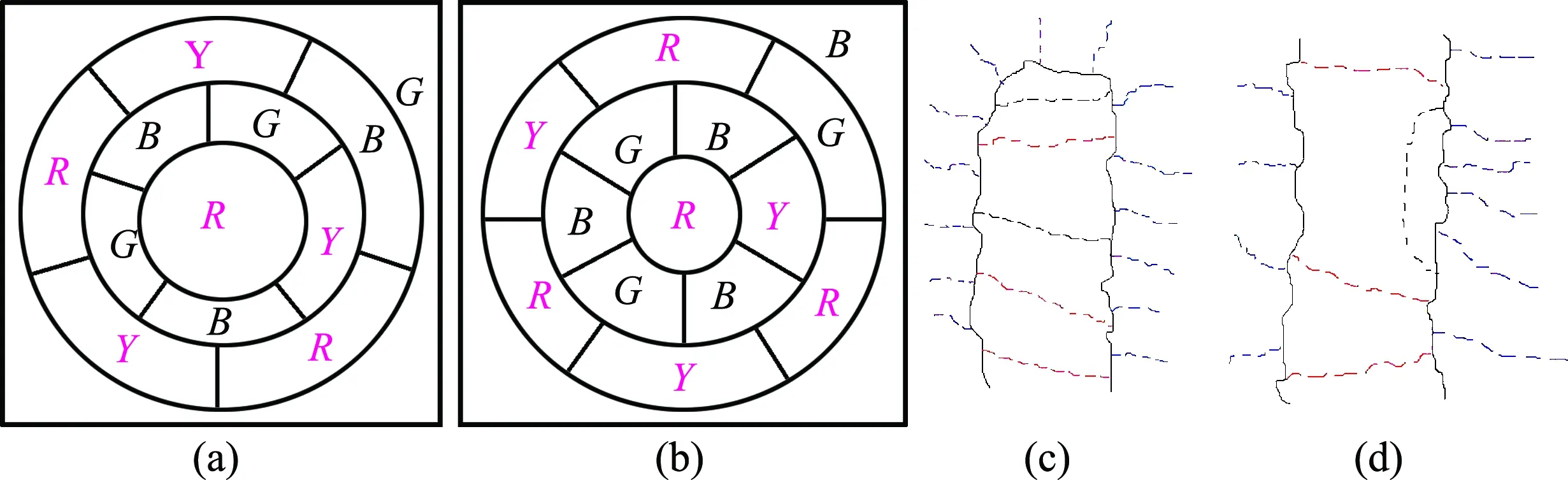
图6 四色解存在性证明

树状结构需要足够的分支点，在基础地图中只有B5不能做分支点．当大量B5区域集中在一起时，形成两个交叉树型结构已不可能，只有产生某一族的环形结构才能形成链路．哈密尔顿图就是这样产生的[9]；例如b25a图，区域组成：1B9+3B8+21B5(基本定理3)，大量B5聚积不可能形成两个交叉树型结构，必须有环形链路结构出现．正如2.3中链路类型和图5(a)指出，环形区域数为偶数，且环形族的区域数和节数相等，其内外的另外一族非环形结构都是区域数比节数多1，故保持区域(r)比节(r-2)的总数多2的基本要求．一族的环形结构将另外一族分割为互不连接的两部分，故不能在同一个一笔画封闭线内，势必分属于两个相互不连接的一笔画封闭线．若环形封闭链路的内(或外)部是另外一族的无环形的树形结构，环路带分支链路的边长度为环路长度与分支链区域长度的2倍之和(它当然是偶数)，它相当所围另外一族的区域集团和区域边界线总和(见2.3中(3))．这可确保环形封闭链路另一侧的外(或内)部的待定结点数为偶数，既保证完整节的生成，也保证边的增加是偶数(基本定理1)．这样一来就可以分别在其内(或外)部按I=2(1+1)的情况处理，不同的是在全图的部分范围内执行，这些内(或外)部的双树型链路结构都可看成孤立点环形结构经过一系列区域增加操作而完成，偶数边的孤立点存在四色解也可得出原双树型链路结构有四色解．按链路定理可知，节是支撑链路的区域连接及主控宽度和方向，边是接受主控的相序一笔画封闭走线并分隔两族．基础地图的2(r-2)个偶数结点，理论上可以形成r-2个完备的节，以及2(r-2)条边线．如果一条边线走遍全图所有结点而没有形成环形链路，则最后构成I=2(1+1)的结果．如果边线走过部分区域已构成封闭一笔画边线，不但已形成环形链路，且环形链路本身的区域数也为偶数，这就使封闭一笔画边线数必为偶数，且环形链路之内(或外)的待定结点数都是偶数，可再次形成完备的节，并构成I>2的结果．显然环路分布遵循如下原则：只有异族环可以相嵌套，同族环则不能相嵌套，同族环可以并立，但必须直接或间接相连．出现多个链路的环形结构将形成I-1个一笔画的偶数条封闭边线，每个结点都有且仅有一个节，各一笔画封闭边线之间仍由这些节支撑．

2.8 基础地图的求解方法

2.7中同时也给出求解的“边-节”探寻法．

当链路无环形结构时，即I=2(1+1)情况，参看图7；任选一个首结点编号为1(红)，由它引出的边有3个方向，在图7(a)中任选一条边的终点编号为2，从2号开始后的所有结点都有3种可能：一是选边有两种可能的可变结点(用蓝色码表示)，选定其边后的另外一条边确定为节，用红虚线表示，这一笔画边线前进时还带一个节对其后操作进行控制．二是进行若干步后出现选边只有一种可能的不变结点(用黑色码表示)，出现不变结点的原因有两个：一个是相邻出现一个早已生成的节的另外一端点，它必须前行(如图7(a)的5号点)，且不必再画新节；另一个是选边之一却和初始点1相连，且一笔画封闭边总数不是偶数，它不能前行，必须选另外一条边；为此都只能选一种．三是前进方向不可以选，它的原因也有两个：一是相邻出现两个节的终点，它无法前行(如图7(b)的17号点)，否则会出现两个节相连的现象(违背链路定理)；另一是一笔画封闭边线已构成，而边的总数不是偶数，为此要作回溯处理：由此点开始沿着数码顺序逆行，每遇见黑码(即不变结点)时，则将码和其伴随的节一起删除(注意：不是其伴随节不可删除)；按此处理直到遇见第一个蓝数码(即可变结点，见图7(b)的11号点)为止，改变蓝色为黑色(即将可变结点变为不变结点)，并改变其前进方向和相应的节(见图7(c)的11号点)，继续前进…直到所有结点都被边跑过，最终回到起始点1处，形成封闭的一笔画线图(有时要补上最后的节)，且边总数是偶数，任何结点都仅连一个节．这种寻“边”前进带“节”控制的方法，是要在偶数2(r-2)个结点和偶数2(r-2)条边中寻找符合链路定理的链路构造，对后面的有环情况也是如此．独联体数为I=2(1+1)的四色解还可能不止一个(见图7(a) 和(c)，是不同的四色解)．

当链路出现某一族的环形结构时，即I>2情况，见图8：一族的环形结构将另一族分隔为相互不连接的内外两部分，每一部分对环形族的一侧则构成一个无环形结构的求四色解问题，如果把对全局的考虑改为对图形的相连接的部分作类似处理，就成为一个无环形结构链路(I=2)的求解问题，它的前提是要求该环形结构的区域本身总数(不包括它的内或外的分支)是偶数即可．如果环形结构本身的区域总数不是偶数，则作前进方向不可选而失败，如前所述逆行顺序查找并处理．这种一部分一部分地考虑，可得到多个受控于节的封闭一笔画边线．图8(a)和(b)是文献[9]的哈密尔顿b25a图的两个带不同环路的解；图8(c)是1B9+6B6+15B5图的带环路的四色解．当区域数量r较大时，如前所言，会有很多对应于不同链路环形结构的四色解．从实用角度考虑，求多个可控封闭一笔画偶数条边线的四色解，更为方便和简捷，所有封闭一笔画偶数条边线的总和是偶数2(r-2)，连接所有结点的节的总和是r-2．

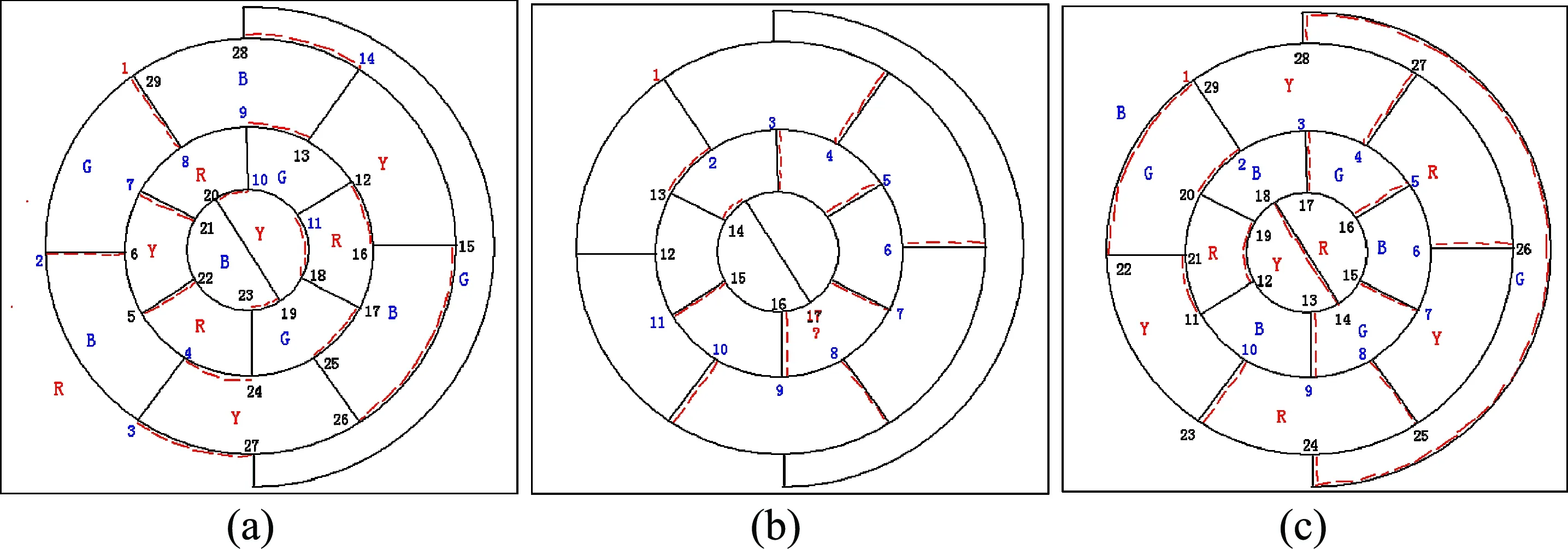
图7 无环路基础地图求四色解方法之例

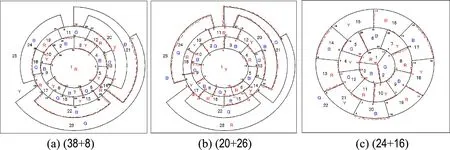
图8 有环路基础地图求四色解方法之例

3 地图求四色解的步骤

地图求四色解的步骤如下：

步骤1 统一编号地图区域．对地图的所有区域进行编号，保证每个区域的编号不缺失又是唯一的即可．

步骤2 无孔洞处理地图．通过装配定理的第一类可移去问题和第二类可移去问题的处理，化原问题为若干个无孔洞且相邻次数不多于1的子地图求四色解问题．(如果有G2是单区域的第二类可移去问题时，也可留后转步骤4．)

步骤3 简单化处理地图．当地图中有阶数大于3的结点时，有许多种方法可将此结点“拉伸”以减少其阶数，使所有结点的阶都是3，从而使地图简单化．生成图转化为原始图的方法很多，它的随意性也影响四色解的结果．

步骤4 基础化处理地图．采用吸收定理来吸收二边、三边、四边区域，至此转化为基础地图求四色解问题．这个处理也有一定随意性．

步骤2～4的处理，只是可能丢掉一些原问题的四色解，绝没有引进原问题之外的新四色解，这在研究解的存在性和求解方法中是完全可以接受的．

步骤5 求解基础地图．每个基础地图都按2.8中的方法求解．(高效的求解方法尚待进一步探讨．)

步骤6 逆向反代求原问题的四色解．此步骤只是步骤1～5的逆过程，由本文所提供的理论和方法可得到原问题的四色解，要特别指出的是按着区域的编号进行着色的交换必须一一对应．

4 结 语

本文针对四色问题，通过定义区域、边界线、结点，将其简化为基础地图的四色解，引入链路得到解的存在性及求解新方法．

致谢：大连理工大学的翁国标老师对本文提出了有价值的建议，在此表示感谢．

[1] Ore O. The Four-Color Problem [M]. New York:Academic Press, 1967.

[2] 邦迪 J A, 默缔 U S R. 图论及其应用[M]. 吴望名,等译. 北京:科学出版社, 1984．

Bondy J A, Murty U S R. Graph Theory with Applications [M]. WU Wang-ming,etal, trans. Beijing:Science Press, 1984. (in Chinese)

[3] 林 寿. 文明之路—数学史演讲录[M]. 北京:科学出版社, 2010.

LIN Shou. Civilization - Mathematical History Lectures on Road [M]. Beijing:Science Press, 2010. (in Chinese)

[4] 张奠庙. 20世纪数学经纬[M]. 上海:华东师范大学出版社, 2002.

ZHANG Dian-miao. A Panorama of the 20th Century Mathematics [M]. Shanghai:East China Normal University Press, 2002. (in Chinese)

[5] 前田渡,伊东正安. 现代图论基础[M]. 陶思雨,王缉惠,译. 北京:高等教育出版社, 1987.

Mayeda W, Ito M. Modern Graph Basis [M]. TAO Si-yu, WANG Ji-hui, trans. Beijing:Higher Education Press, 1987. (in Chinese)

[6] YANG Ming-sheng . Exploration of solutions to the four color problem [J]. International Journal of Analyzing Methods of Components and Combinatorial Biology in Mathematics, 2008, 1(1):27-38

[7] 杜布洛文 Ь A,诺维可夫C Л,福明柯 A T. 现代几何学:方法与应用[M]. 徐明,译. 北京:高等教育出版社, 2006.

Dubrovin B A, Novikov S P, Fomenko A T. Modern Geometry: Methods and Applications [M]. XU Ming, trans. Beijing:Higher Education Press, 2006. (in Chinese)

[8] Tomescn I. 组合学引论[M]. 北京:高等教育出版社, 1985.

Tomescn I. Introduction to Combinatorics [M]. Beijing:Higher Education Press, 1985. (in Chinese)

[9] 徐寿椿. 图说四色问题[M]. 北京:北京大学出版社, 2008．

XU Shou-chun. Four Color Problem by Graph [M]. Beijing:Peking University Press, 2008.

(第56卷卷终)

Graph theory of four-color— Existence and searching method of solution for four-color problem

YANG Ming-sheng*

( Research Institute of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China )

Another new system of graph theory is established directly from four-color problem. By defining the region, boundary line, node, etc., after breaking down the complicated map into several connected single-layer subgraphs and simplifying them, three fundamental theorems of this system are obtained. And using chain, the solution existence and searching method of four-color problem related to any map with limited regions are given.

graph theory; four-color problem; region; boundary line; node; chain

2016-05-15；

2016-07-26．

杨名生*(1938-)，男，教授.

1000-8608(2016)06-0662-09

O157.6

A

10.7511/dllgxb201606016