拖曳水池阻塞效应对不同船型影响数值研究

赵 大 刚， 郭 春 雨， 阚 梓

( 哈尔滨工程大学 船舶工程学院， 黑龙江 哈尔滨 150001 )



拖曳水池阻塞效应对不同船型影响数值研究

赵 大 刚*， 郭 春 雨， 阚 梓

( 哈尔滨工程大学 船舶工程学院， 黑龙江 哈尔滨 150001 )

在进行变尺度船模系列试验、大尺度船模自航试验、几何相似船模尺度效应试验或者比较不同尺度水池的试验结果时，必然要遇到阻塞效应问题．在水池尺度较小、船模尺度相对较大时，阻塞效应尤其突出．阻塞效应混在各种分析结果中，影响结论的准确性，必须予以修正．采用计算流体力学(CFD)方法，通过改变计算域的大小来改变阻塞比，利用流体体积分数(VOF)方法捕捉船舶的自由液面，计及升沉和纵倾两个自由度，对两种船型进行了不同阻塞比、不同航速下的阻力数值计算，探究船型、水池宽度和深度与阻塞效应影响程度的关系，获得了阻塞效应的影响规律，并对拖曳水池的阻塞效应修正提出了合理化建议．

阻塞效应；阻力修正；拖曳水池；多自由度；计算流体力学(CFD)

0 引 言

船模拖曳水池阻力试验所得阻力值通常大于同样速度在无限流域中的数值，其中阻力值的增加主要来自水池边界的影响．根据流体力学相关理论分析水池边界效应产生的原因如下：第一，池底和池壁限制了绕船模的水流流动使回流速度增大，导致黏性阻力变化，这被称为阻塞效应；第二，深度有限的池底不仅使回流速度增大，船体吃水增大，船体周围的流场发生变化，引起黏性阻力改变，而且对于波长相同的波浪来说，浅水中的波速小于深水中的波速，因此船模兴起的波系也不同于无限场流域中的波系，导致兴波阻力不同，这是所谓的浅水效应；第三，池壁的限制使船模兴起的波系遇到池壁反射回来，与原波系相互叠加干扰，兴波阻力发生变化，这通常被称为池壁效应．在拖曳水池进行试验时，船模航速通常不会达到0.5倍Frh(水深弗劳德数)，根据水波理论，Frh小于0.5时，浅水中兴起的波系与深水中的波系几乎一致，而且根据开尔文对于压力点兴波的描述，池壁反射的兴波很难到达船身，因此浅水效应和池壁效应可以忽略，阻塞效应作用影响最大[1-3]．

国际拖曳水池会议(ITTC)很早就提出了阻塞效应的修正公式，在多届ITTC大会上，水池边界影响被学者们重点讨论[4-7]．在1934年，苏联的什利赫金格和什特罗布什就提出了一个半经验公式，根据深水中的船舶阻力得到浅水中的船舶阻力，对航行速度进行了修正[8]．在英国国家物理实验室水池和荷兰试验水池中也进行过一系列的船模试验，得到了剩余阻力与航道阻塞比的关系并绘制了相应曲线，该曲线可以近似地确定受航道影响的剩余阻力系数的变化，并得出：如果船模的船舯横剖面面积不超过水池横断面的1/250，那么模型不受航道的影响[9]．英国的斯科菲尔德在《限制性水道中船舶的航速》一文中总结出船舶在限制航道中与在大海中航行的主要差别有三：其一是船体周围有明显的循环水流；其二是靠近尾部存在不同于在大海中航行时的尾波浪；其三是若限制航道中的船速与大海航行时的船速一致时，限制航道中的船舶要大幅度地增加功率[10]．谢克振等以10条船模在不同断面水池(同一水池通过隔板改变断面形状)进行了船模阻力试验，并根据试验结果对第13届ITTC性能委员会提出的阻塞效应修正公式进行了论证、研究，指出：除浅水池外的通常尺度比的水池中，水池宽度比水池深度对阻力的影响更大[11]．盛振邦等指出，拖曳水池中的船模的浅水效应与池壁效应通常可以忽略不计，阻塞效应是水池边界效应的主要部分[12]．施奇等指出，在船模拖曳水池阻力试验中，水池深度对船模试验结果影响较大，但没有给出具体的修正方法[13-14]．李广年等根据浙江海洋大学水池中的5次试验结果及相关理论成果指出：阻塞比小于0.2%时，阻塞效应可不计及，池底的影响随船模设定速度的增大而增大[15]．周广利等在研究船模阻力试验的不确定度因素时，对阻塞效应进行了分析，利用ITTC公式对速度进行了修正，但是并没有对修正公式提出改进[16-20]．

随着计算流体力学(CFD)的发展，国内外众多学者采用CFD方法进行了一系列船舶水动力的相关研究．由于模型试验耗费人力物力，而CFD方法兼具理论性和实践性的双重特点，既能考虑黏性的影响，同时对自由液面的捕捉、运动响应的模拟都能很好的实现，不失为一种研究水池阻塞效应的新方法．清华大学刘彦伟等在验证水洞减阻措施的有效性试验中，采用CFD软件对水洞边界有限制的模型和边界无限制的模型进行模拟，指出在阻塞比超过25%时，有限和无限流域情况下船舶摩擦阻力系数相差很大，并且提出增加工作段尺度可有效减小这一影响[21]．

本文选取散货船和集装箱船两种船型为研究对象，通过改变计算域的大小来改变阻塞比，即保持计算域宽度不变按比例缩小深度、保持计算域深度不变按比例缩小宽度，计算两种船型在这两种阻塞比变化方式及3种航速下的船舶阻力．数值研究中计及升沉和纵倾两个自由度，利用流体体积分数(VOF)方法捕捉船舶的自由液面，进行船模在不同阻塞比、不同航速下的阻力试验的数值模拟，探究水池宽度、深度与阻塞效应影响程度的关系，对结果进行分析，并提出阻力修正方案．

1 阻塞效应修正理论

船舶横截面面积与航道断面面积的比值称为阻塞比．本文主要采用3种定义方式：

m1=CmBT/A

式中：A代表试验水池的断面面积，B代表船模宽度，T代表船模吃水，Cm代表船模的舯剖面系数，Lwl代表水线长，代表排水体积．

目前对阻塞效应修正最为简便的方法是对速度进行修正．对速度修正的原理大致可分为两类．第一类是建立在所谓的平均流理论基础上，认为水池边界的存在使船舶周围的水流对远前方而言有一个平均的速度增量．从连续性方程及伯努利方程出发，经略去Δv/v的高阶项即可推得

(1)

第二类是所谓的风洞理论．用源汇分布代替回转体，应用一系列映射的方法计算池壁所引起的势流速度增量，推导出的公式形式为

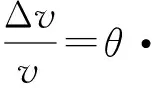
(2)

式中：θ是Re和船型的函数，本文中引用这一形式即斯科特(Scott)公式，对75000DWT散货船θ=1.92-0.129×10-6Re，对KCS集装箱船θ=1.86-0.072×10-6Re．Re=v·Lwl/υ为雷诺数，其中υ代表运动黏性系数．

另外如果用一对源汇在同轴圆柱中心线处运动的简化，可推得一个简化因子，并考虑自由液面的下降，即可得出：

(3)

式(3)即为简化田村公式(Tamura simplified)．其中L为船模长度，b为水池宽度．

这二类方法的优点是比第一类平均流理论多考虑到了速度随与物体距离而变化的影响，比平均流理论进一步．此类公式也同样可借助试验结果引入经验修正因子，如式(2)中θ是Re和船型的函数．即说明这3种类型的公式对阻塞效应考虑的敏感程度是不同的．相对而言，平均流理论的公式较不敏感，田村类型的公式次之，斯科特类型的公式最敏感．究竟哪一种公式较合适，需要用试验的方法来检验．

2 研究对象

表1 模型主要参数

本文计算模型的船体周围网格划分如图1所示．

(a) 75000DWT散货船

(b) KCS集装箱船

图1 计算域网格划分

Fig.1 Mesh of computational domain

船身周围的网格较密，可以避免船体运动引起的船体周围细小网格的扭曲，并且保持了必要的计算精度；离船体较远的区域，网格稀疏，有效降低了网格数量，节省了计算时间，并且船体运动过程中的运动幅度相对于此处的网格尺度不大，网格变形率降低．

3 不同阻塞比对船舶性能的影响研究

分析计算结果时，首先进行了网格无关性的验证，并将CFD的计算结果与试验值进行了比较，计算结果接近．表2是75000DWT散货船和KCS集装箱船计算值与试验值对比，证明了使用该方法进行数值研究的可行性．

3.1 水池宽度对船舶波形及流线的影响

通过改变计算域的大小，模拟不同阻塞比条件时的船模阻力试验．分别模拟了固定水池宽度等比例缩小水池深度、固定水池深度等比例缩小水池宽度时的船模阻力试验，并与无限流域时的情况进行对比．

表2 计算值与试验值对比

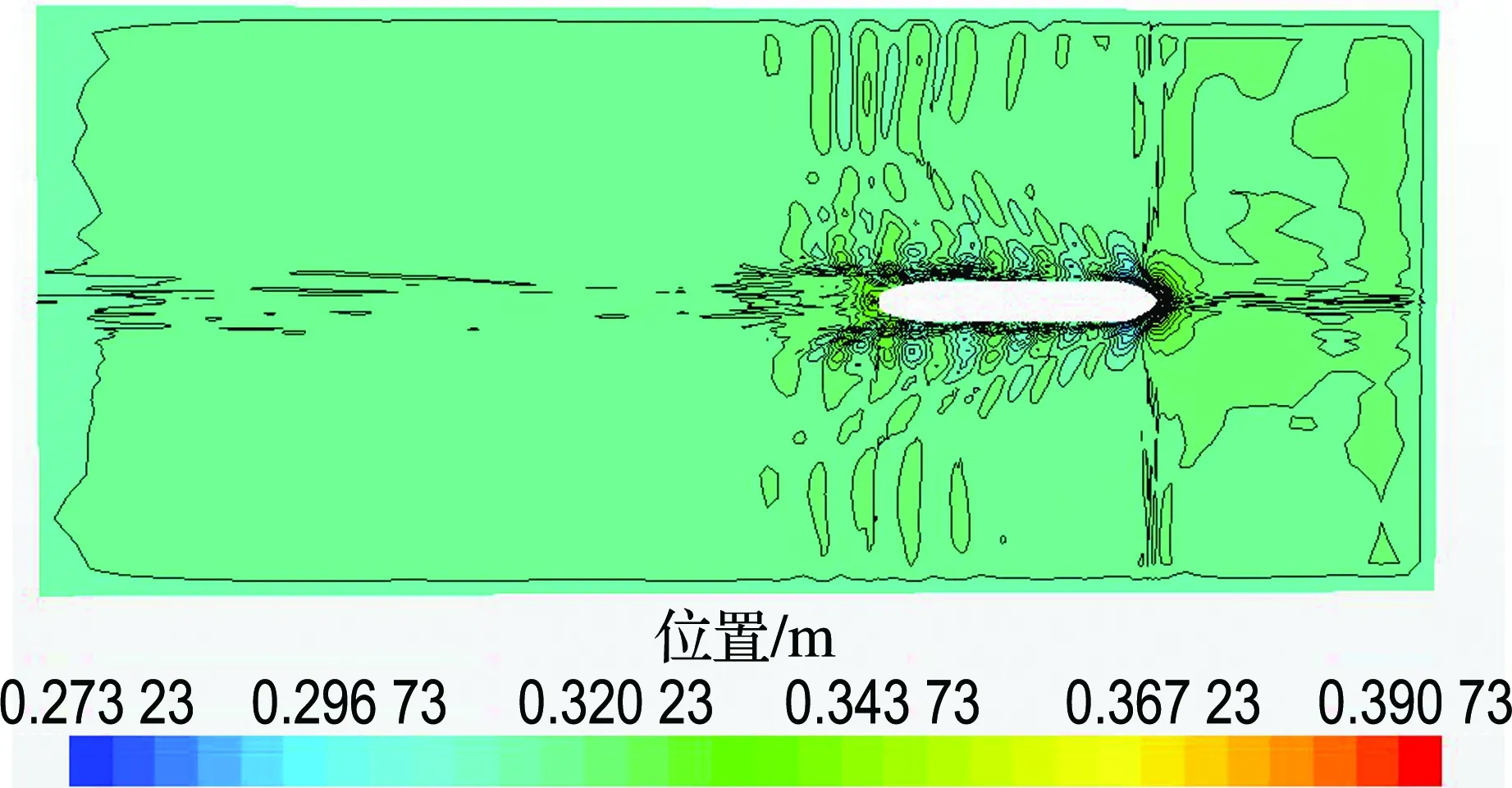
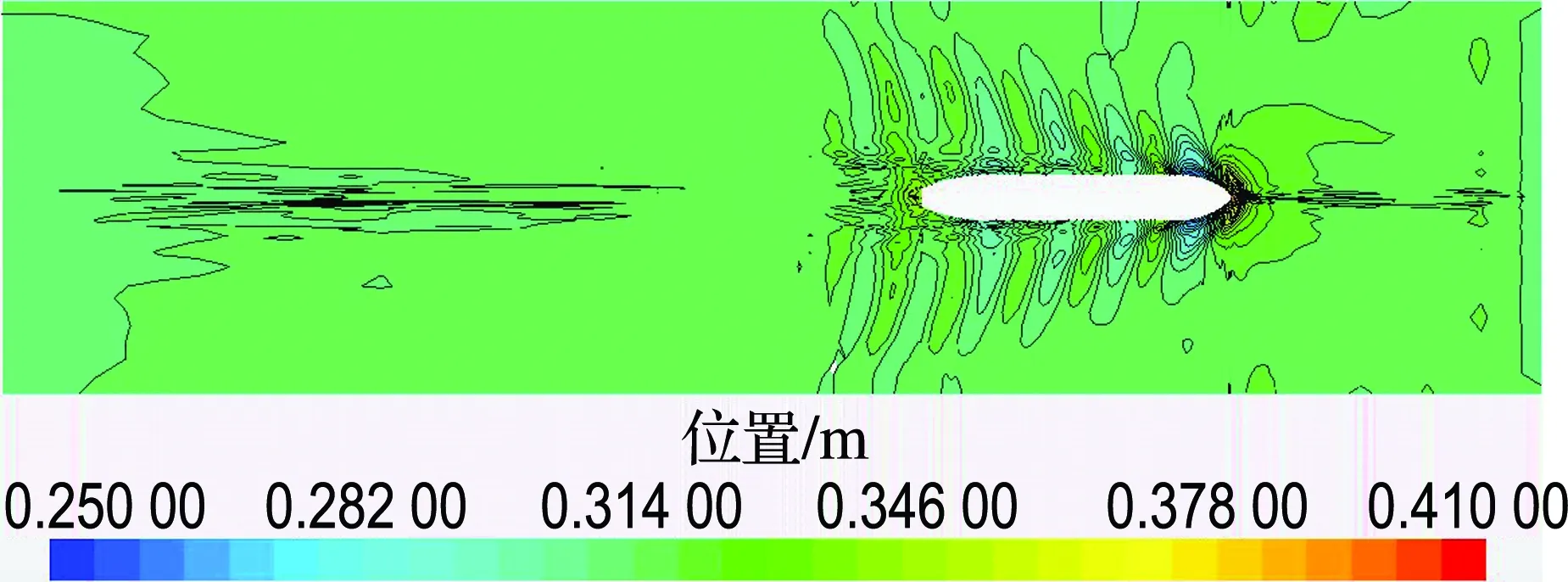
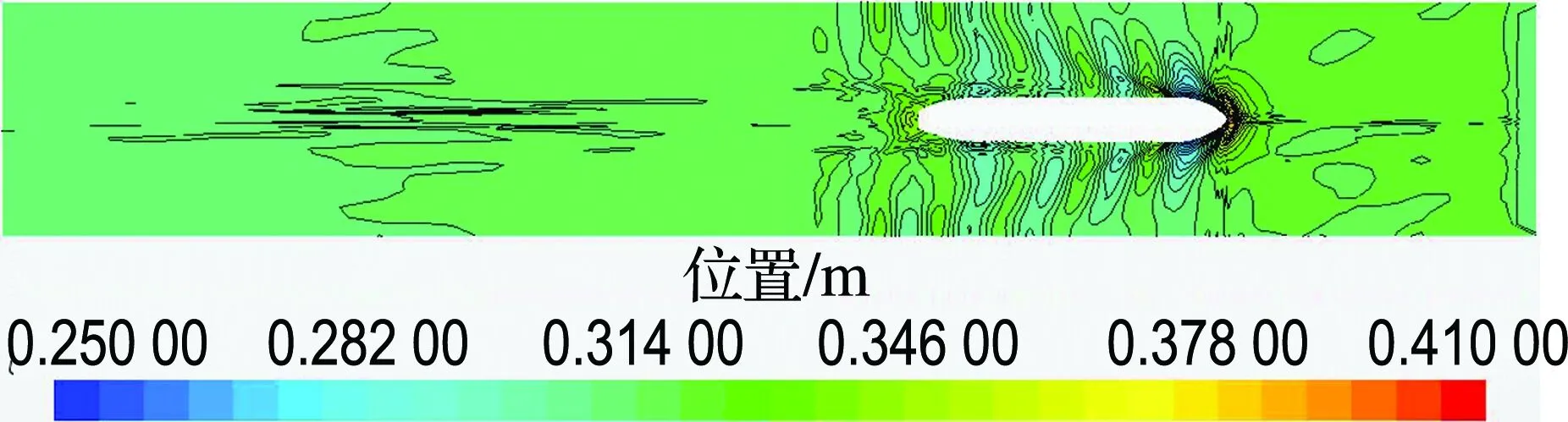
在数值计算时，由于水池宽度的缩小，不可避免地将涉及池壁效应的影响，因此本文先对FrL为0.28时的75000DWT散货船和KCS集装箱船无限流域、水池比例(尺寸与哈尔滨工程大学船模拖曳水池截面相同：宽7 m、水深3.5 m)、70%水池比例(截面的宽度和深度为水池截面的70%)3种情况下的波形等高线图进行比较，如图2、3所示．

从图中可以看出：与无限流域相比，水池比例的波形与之相差不大，说明在该截面的水道进行试验有对无限流域修正的可能．在70%水池比例时，开尔文波系的衍生已经明显受到了水池边界的影响，其反射回来的波系会对船体产生影响，这意味着池壁效应的影响已经产生．

随着FrL的增大，阻塞效应愈加明显．为进一步研究阻塞效应的影响规律，对FrL为0.28时的KCS集装箱船无限流域、水池比例情况下的流场和流线图进行了比较，如图4所示．

(a) 无限流域

(b) 水池比例

(c) 70%水池比例

图2 75000DWT散货船波形等高线图

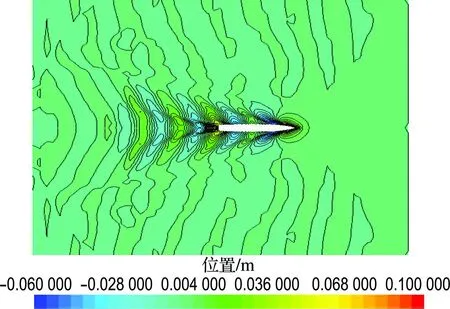
(a) 无限流域

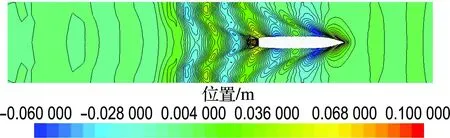
(b) 水池比例

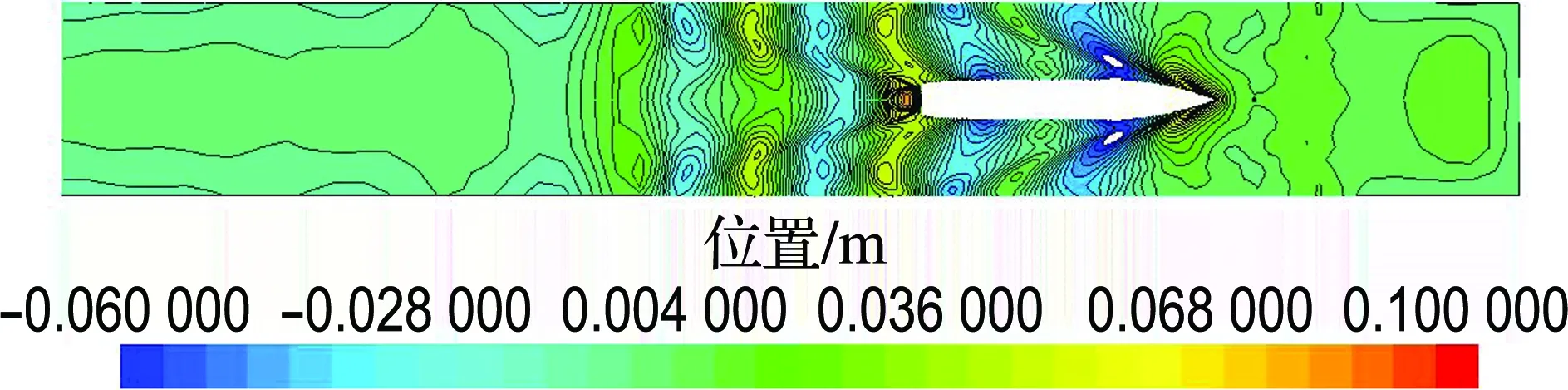
(c) 70%水池比例

图3 KCS集装箱船波形等高线图

Fig.3 The waveform contour map of KCS container ship

从图4可以看出，在船艏处有明显的水流速度增大，这说明水流的拥堵主要集中在船艏．随后对船身y/Lpp=0.074处的波高进行分析，提取KCS船型无限流域、水池比例以及70%水池比例时的波高分布曲线，如图5所示，该图的原点位于船艉，正方向是船艉向船艏的方向．

(a) 无限流域

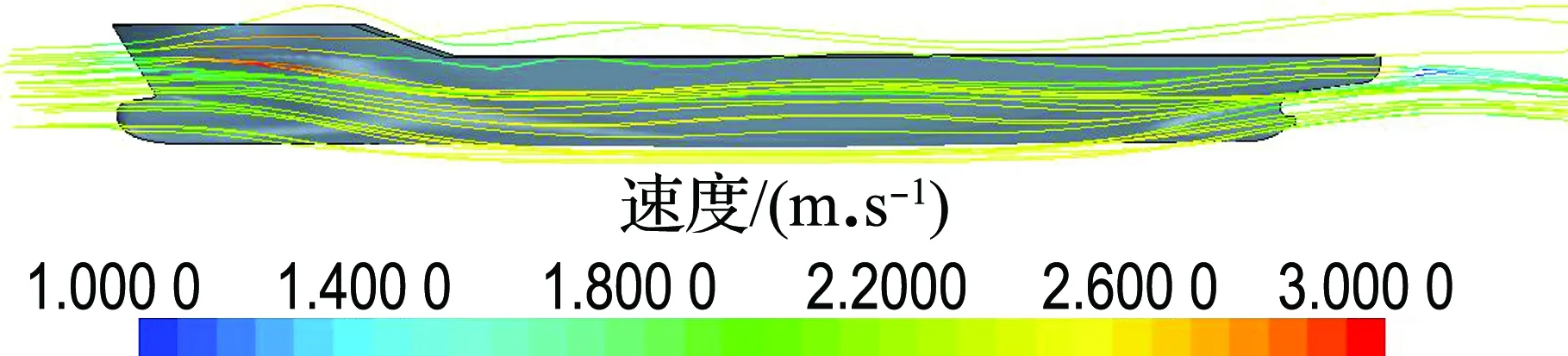
(b) 水池比例

(c) 70%水池比例

图4 KCS集装箱船流线图

Fig.4 The flow chart of KCS container ship

从图5可以看出，随着计算域尺度的减小，船身附近的波高变化较大，波峰和波谷值变大．因此，阻塞效应会对船身附近的波高产生较大影响，进而影响船模阻力．

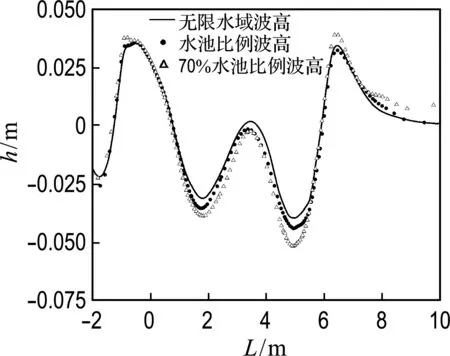
图5 KCS船型波高分布

3.2 水池宽度、深度对船模阻力的影响

3.2.1 75000DWT散货船阻力计算结果 对75000DWT散货船进行了不同航速、不同阻塞比情况下的阻力计算，计算结果见表3～5．

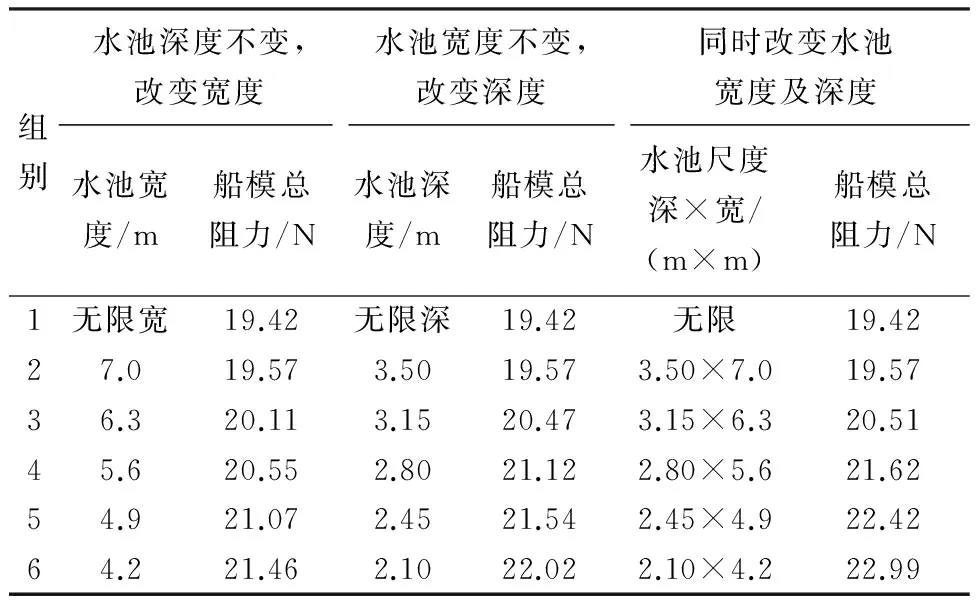
表3 v=1.139 m/s计算结果

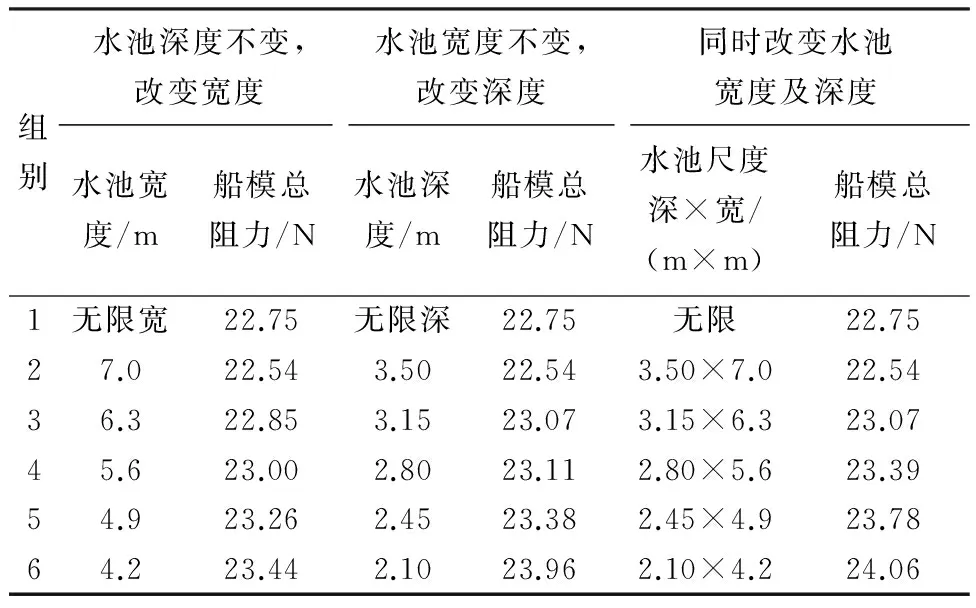
表4 v=1.220 m/s计算结果

从表中可以看出，随着阻塞比及船模速度的增大，船模阻力也随之增大．从v=1.220 m/s状态下的计算数据可以看出，水池深度变化时的阻力值和水池深度、宽度同时变化时的阻力值更加接近，意味着这部分阻力的增加主要来源于水池深度的变化，其他速度点的各组别均遵循这一规律．因此可以得出结论：在航速较低时，水池深度对阻塞效应影响程度更大．

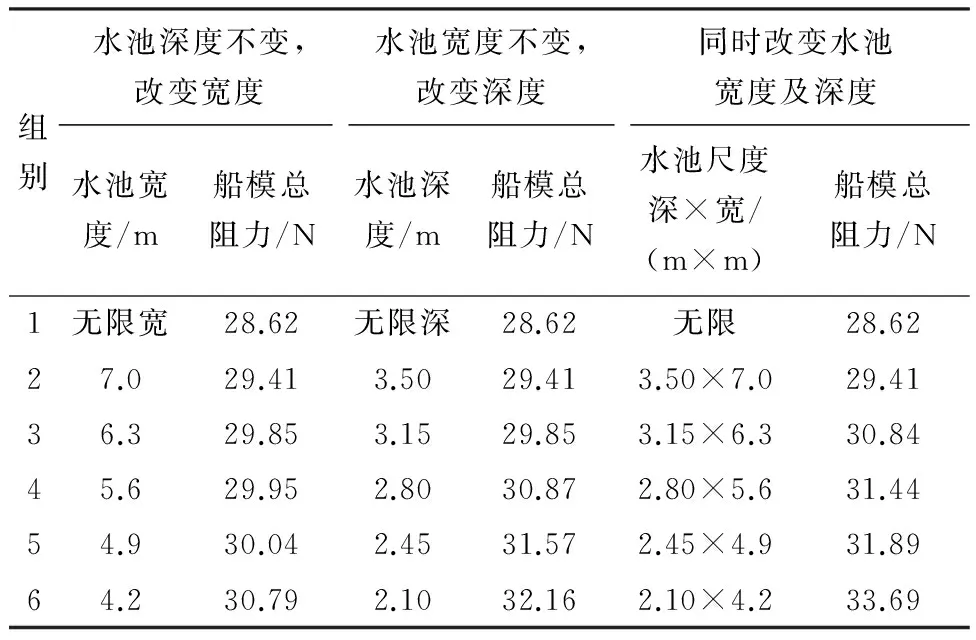
表5 v=1.342 m/s计算结果

3.2.2 KCS集装箱船阻力计算结果 对KCS集装箱船进行了不同航速、不同阻塞比情况下的阻力计算，计算结果见表6～8．

根据表6～8的数据，运用与75000DWT散货船同样的分析方法，可以看出，随着FrL的增大，此时对阻塞效应影响程度更大的是水池宽度．

表6 v=2.013 m/s计算结果

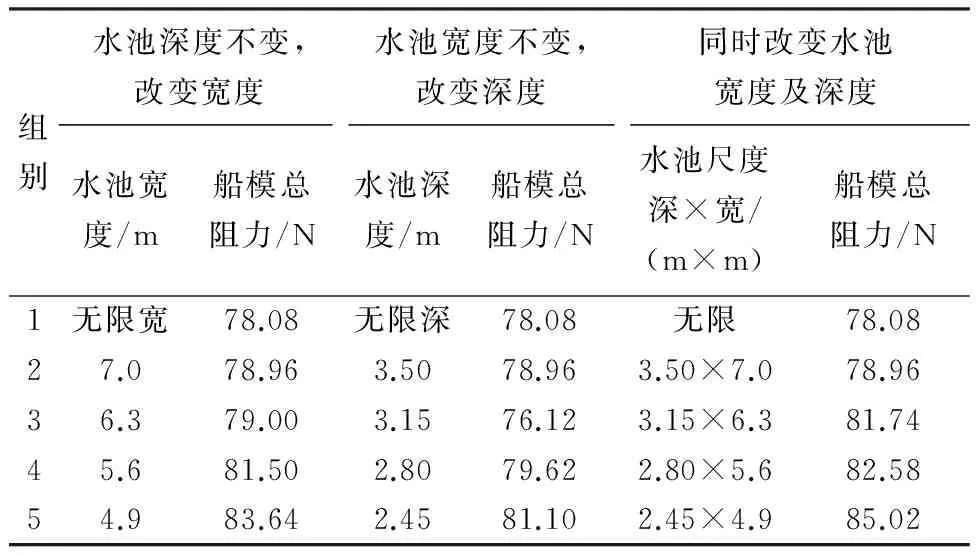
表7 v=2.196 m/s计算结果

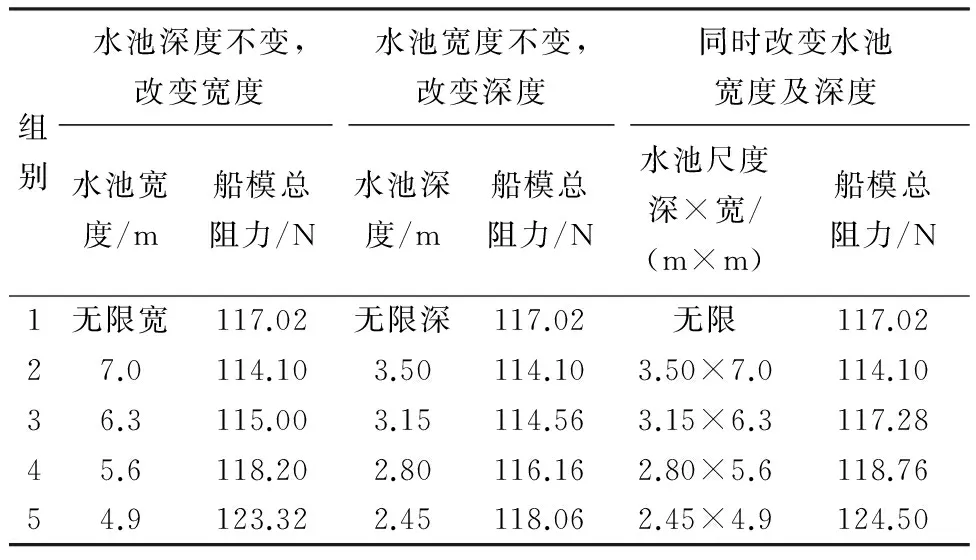
表8 v=2.379 m/s计算结果

3.3 水池宽度、深度对纵倾和吃水的影响

本文着重考虑了水池的深度变化和宽度变化对船体姿态的影响．在模型数值计算中，计及升沉和纵倾两个自由度．基于此观察在阻塞比变化时船模的运动姿态变化．表9、10是75000DWT散货船在航速v=1.342 m/s时的船身姿态变化；表11、12是KCS集装箱船在航速v=2.379 m/s时的船身姿态变化．其中表9和表11是固定宽度等比例缩小深度时的纵倾、升沉变化；表10和表12是固定深度等比例缩小宽度时的纵倾、升沉变化．

表9 75000DWT散货船船身姿态变化(宽度不变，深度改变)

Tab.9 The hull posture change of 75000DWT bulk cargo ship (the same width, but different depths)

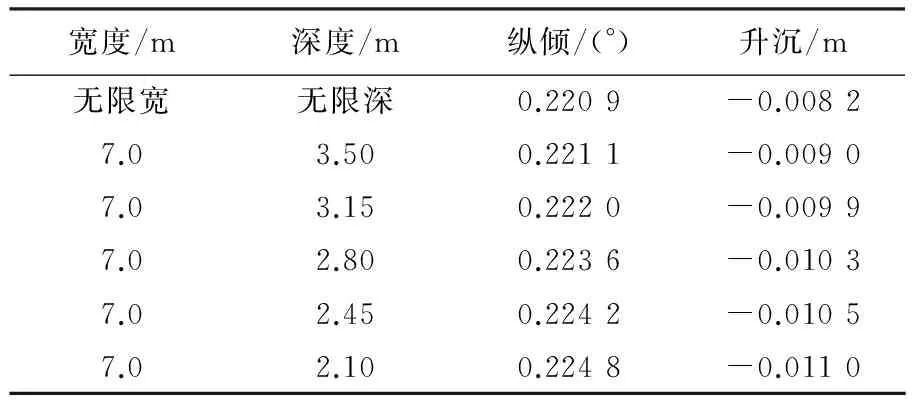
宽度/m深度/m纵倾/(°)升沉/m无限宽无限深0.2209-0.00827.03.500.2211-0.00907.03.150.2220-0.00997.02.800.2236-0.01037.02.450.2242-0.01057.02.100.2248-0.0110

表10 75000DWT散货船船身姿态变化(深度不变，宽度改变)

Tab.10 The hull posture change of 75000DWT bulk cargo ship (the same depth, but different widths)

宽度/m深度/m纵倾/(°)升沉/m无限宽无限深0.2209-0.00827.03.500.2211-0.00906.33.500.2216-0.00955.63.500.2234-0.01004.93.500.2264-0.01054.23.500.2275-0.0108

表11 KCS集装箱船船身姿态变化(宽度不变，深度改变)

Tab.11 The hull posture change of KCS container ship (the same width, but different depths)

宽度/m深度/m纵倾/(°)升沉/m无限宽无限深0.132140-0.016847.03.500.137712-0.019757.03.150.139157-0.020257.02.800.139844-0.021277.02.450.140215-0.02296

表12 KCS集装箱船船身姿态变化(深度不变，宽度改变)

Tab.12 The hull posture change of KCS container ship (the same depth, but different widths)

宽度/m深度/m纵倾/(°)升沉/m无限宽无限深0.13214-0.016847.03.500.13770-0.019756.33.500.13420-0.021235.63.500.14470-0.021774.93.500.14890-0.02203

由上表可以看出，在较低航速时，船体姿态变化较小．根据边界层理论和伯努利方程可知，该现象是符合实船真实航行状态的．从各个数据表横向的比较可以看出，宽度的变化对纵倾的影响更大一些，这是受到开尔文波系被边界反射影响所致．而深度的变化对升沉的影响更大，这是由于受到池底效应的影响．在航速较大时，阻塞效应对升沉的影响比对纵倾的影响更加明显．

4 不同修正方案对比

为了便于对船舶阻塞效应修正后的结果进行比较，本文引入修正系数

(4)

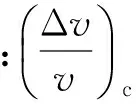
本文对斯科特公式、简化田村公式以及3种不同阻塞比定义的平均流理论公式的修正结果进行了对比．

4.1 75000DWT散货船阻力修正

根据75000DWT散货船的数据计算，斯科特公式可表述为

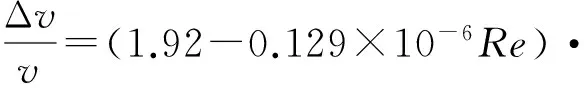
(5)

简化田村公式可表述为

(6)

平均流理论修正公式如下

(7)

分别对水池比例以及90%、80%、70%、60%水池比例(计算域宽度和深度分别同比例缩小)情况下的船模阻力进行修正，修正结果对比如图6所示．

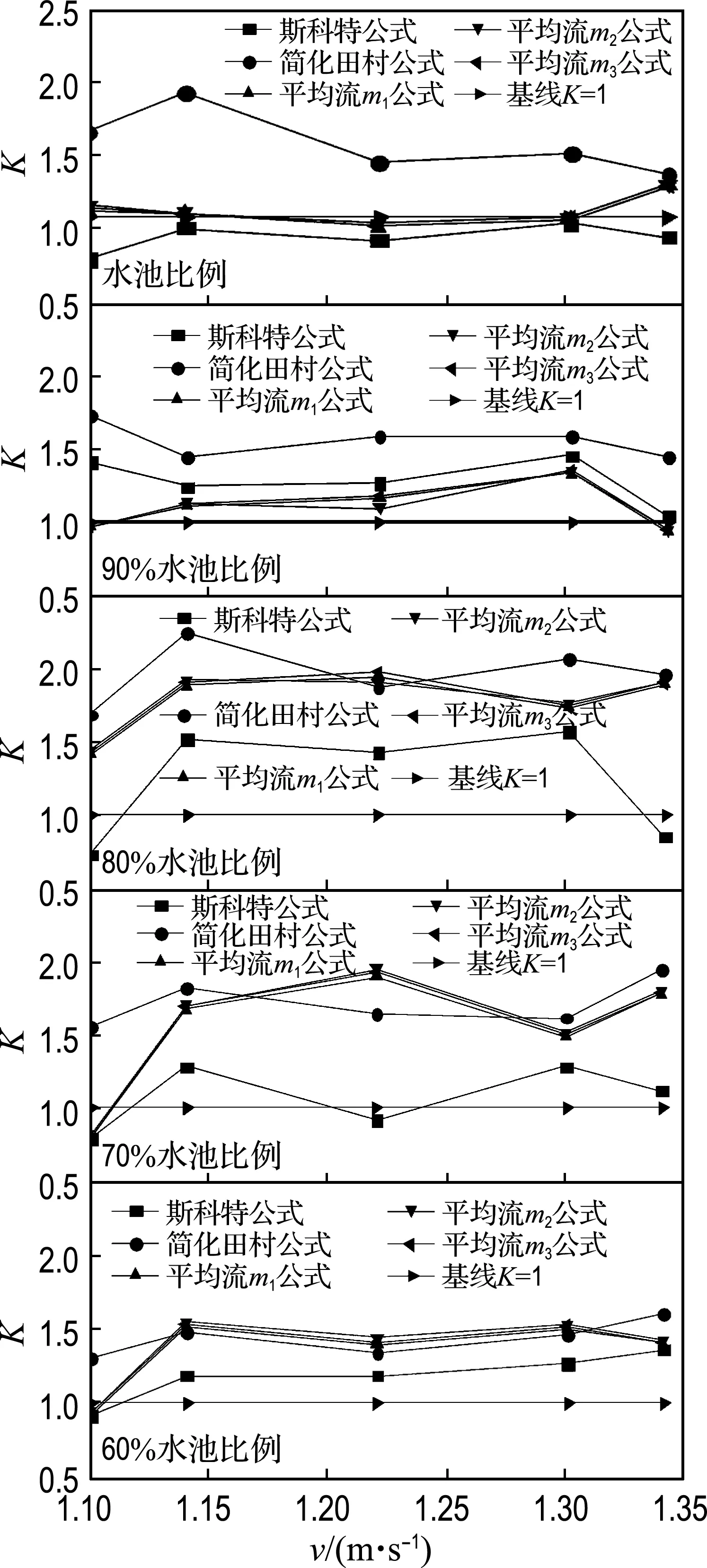
图6 修正结果对比

从图6可以看出，在阻塞比较小时，即在水池比例和90%水池比例情况下，可以选用平均流理论对阻力进行修正，且不同阻塞比的定义下修正结果差别很小；当阻塞比较大时，选用斯科特公式能得到更好的修正结果．

4.2 KCS集装箱船阻力修正

由于75000DWT散货船设计航速对应的FrL较小，而KCS集装箱船设计航速对应的FrL相对较大，且为了研究不同船型的阻塞效应修正方法，又对KCS集装箱船在船模速度分别为2.013、2.196、2.379 m/s时的船模阻力进行了修正．根据斯科特提出的修正公式，随着船型和FrL的变化，公式中的形式及其中常数会有所变化，根据文献[11]中提供的计算方法，得到KCS集装箱船的修正公式如下：

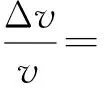
BL2[2.4×(FrL-0.12)2]A

(8)

而简化田村公式和平均流理论修正公式的形式是固定的，因此式(6)、(7)同样适用于KCS集装箱船的阻力修正．

分别对水池比例以及90%、80%、70%水池比例(计算域宽度和深度分别同比例缩小)情况下的船模阻力进行修正，修正结果见表13～16．

表13 水池比例修正结果对比

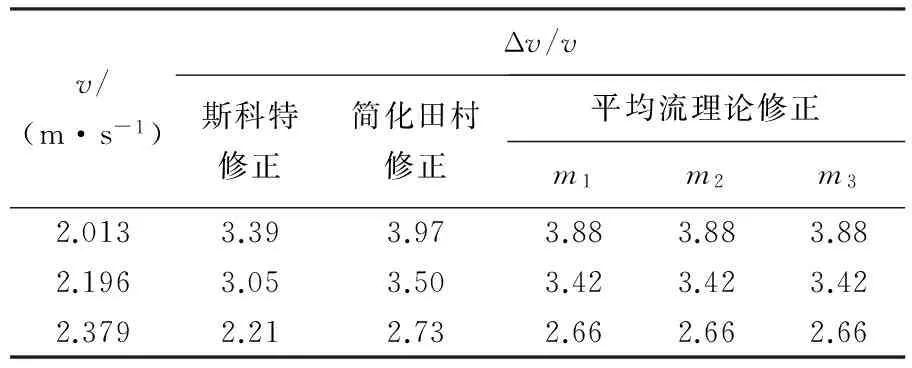
表14 90%水池比例修正结果对比

从以上数据可以看出，FrL大于0.2时，即使在阻塞比较小的情况下，即在水池比例和90%水池比例情况下，选用斯科特公式比选用平均流理论公式修正的效果更好．

表15 80%水池比例修正结果对比

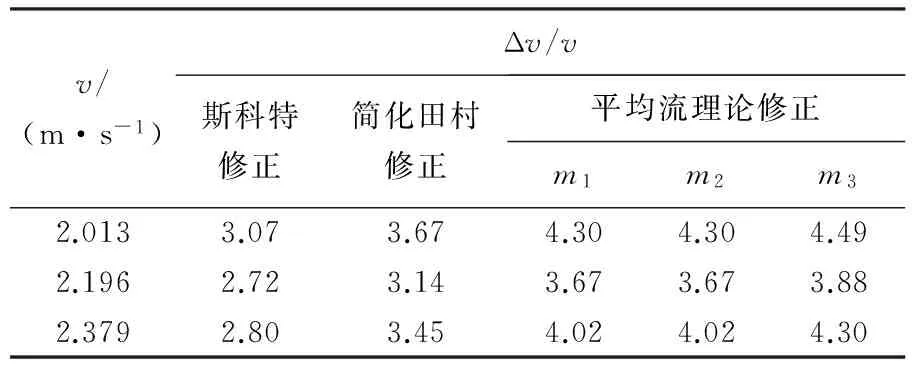
表16 70%水池比例修正结果对比

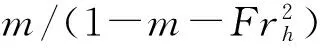
5 结 论

(1)在航速较低，即FrL小于0.2时，水池深度对阻塞效应的影响程度更大；FrL大于0.2时，水池宽度对阻塞效应的影响程度更大，并且随着阻塞比的增大，水池池壁效应的影响程度越来越大．

(2)对哈尔滨工程大学拖曳水池的阻塞效应进行修正，当阻塞比小于0.01且FrL小于0.2时，推荐使用平均流公式进行修正，且3种阻塞比的选择对修正结果影响不大；当FrL大于0.2或阻塞比大于0.01时，推荐使用斯科特公式进行修正．

(3)阻塞效应的产生主要是由船艏对水流的拥堵造成的．

(4)船舶方型系数对阻塞效应的修正有很大的影响，不同的船型所适用的修正公式不同．尤其在选用斯科特公式进行修正时，需要充分考虑方型系数的影响，必要时应根据经验对修正公式补充经验修正因子．

[1] 郝亚平. 船舶性能试验技术[M]. 北京:国防工业出版社, 1989.

HAO Ya-ping. Experimental Technique of Ship Performance [M]. Beijing:National Defense Industry Press, 1989. (in Chinese)

[2] 俞湘三,陈泽梁,楼连根,等. 船舶性能实验技术[M]. 上海:上海交通大学出版社, 1991.

YU Xiang-san, CHEN Ze-liang, LOU Lian-gen,etal. Experimental Technique of Ship Performance [M]. Shanghai:Shanghai Jiao Tong University Press, 1991. (in Chinese)

[3] 李云波. 船舶阻力[M]. 哈尔滨:哈尔滨工程大学出版社, 2006.

LI Yun-bo. Ship Resistance [M]. Harbin:Harbin Engineering University Press, 2006. (in Chinese)

[4] ITTC. Uncertainty analysis for experimental fluid dynamics [C] // 22nd International Towing Tank Conference. Seoul:ITTC, 1999.

[5] ITTC. Uncertainty analysis in EFD, uncertainty assessment methodology [C] // 22nd International Towing Tank Conference. Seoul:ITTC, 1999.

[6] ITTC. Resistance, uncertainty analysis example for resistance test [C] // 23rd International Towing Tank Conference. Venice:ITTC, 2002.

[7] ITTC. Ship models [C] // 23rd International Towing Tank Conference. Venice:ITTC, 2002.

[8] Millward A. A review of the prediction of squat in shallow water [J]. Journal of Navigation, 1996, 49(1):77-88.

[9] Okajima A, Yi D, Kimura S,etal. The blockage effects for an oscillating rectangular cylinder at moderate Reynolds number [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69-71:997-1011.

[10] Mendes A C, Kishev R, Kolodziej J A. Measurements of hydrodynamic loading on a large scale jacket structure under waves and current [J]. Transactions on the Built Environment, 2001, 56:13-24.

[11] 谢克振,周占群,宋家瑾,等. 水池阻塞效应的试验探讨[J]. 上海船舶运输科学研究所学报, 1978(2):1-27. XIE Ke-zhen, ZHOU Zhan-qun, SONG Jia-jin,etal. Experimental study on blocking effect of water pool [J]. Journal of Shanghai Ship and Shipping Research Institute, 1978(2):1-27. (in Chinese)

[12] 盛振邦,刘应中. 船舶原理[M]. 上海:上海交通大学出版社, 2003.

SHENG Zhen-bang, LIU Ying-zhong. Principle of Ship [M]. Shanghai:Shanghai Jiao Tong University Press, 2003. (in Chinese)

[13] 施 奇,杨大明,尹赟凯. 船模拖曳水池静水阻力比对试验研究[J]. 江苏科技大学学报(自然科学版), 2011, 25(4):312-314, 325.

SHI Qi, YANG Da-ming, YIN Yun-kai. Resistance test of ship model in towing tank [J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2011, 25(4):312-314,325. (in Chinese)

[14] 施 奇,杨大明,尹赟凯. 拖曳水池船模阻力试验不确定度分析[J]. 江苏科技大学学报(自然科学版), 2010, 24(5):428-433.

SHI Qi, YANG Da-ming, YIN Yun-kai. Uncertainty analysis of ship model resistance test in towing tank [J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2010, 24(5):428-433. (in Chinese)

[15] 李广年,谢永和,郭 欣. 拖曳水池方案设计[J]. 中国造船, 2011, 52(3):109-114.

LI Guang-nian, XIE Yong-he, GUO Xin. Design of towing tank [J]. Ship Building of China, 2011, 52(3):109-114. (in Chinese)

[16] 周广利,黄德波,李凤来. 船模拖曳阻力试验的不确定度分析[J]. 哈尔滨工程大学学报, 2006, 27(3):377-381, 390.

ZHOU Guang-li, HUANG De-bo, LI Feng-lai. Uncertainty analysis of ship model towing resistance test [J]. Journal of Harbin Engineering University, 2006, 27(3):377-381, 390. (in Chinese)

[17] 周广利. 船模拖曳阻力试验的不确定度分析[D]. 哈尔滨:哈尔滨工程大学, 2002.

ZHOU Guang-li. Uncertainty analysis of ship model towing resistance experiment [D]. Harbin:Harbin Engineering University, 2002. (in Chinese)

[18] WU Bao-shan. On geometric parameters in uncertainty analysis of measurement in ship model test [J]. Journal of Ship Mechanics, 2007, 11(3):363-372.

[19] SHEN Hong-cui, HE Mo-qin, ZHOU Yi. Uncertainty analysis of resistance test [J]. Journal of Ship Mechanics, 1999, 3(6):1-11.

[20] 刘卫斌,吴华伟. 船模阻力试验不确定度评定改进技术研究[J]. 中国造船, 2004, 45(S):22-29.

LIU Wei-bin, WU Hua-wei. Uncertainty analysis in ship model resistance test [J]. Ship Building of China, 2004, 45(S):22-29. (in Chinese)

[21] 刘彦伟,刘 莹. 水洞试验中阻塞比对阻力测量影响的数值模拟[J]. 实验技术与管理, 2007, 24(12):44-47.

LIU Yan-wei, LIU Ying. Numerical simulation of the effect of blockage ratio on drag measurement in water tunnel test [J]. Experimental Technology and Management, 2007, 24(12):44-47. (in Chinese)

Numerical study of influence of blockage effect of towing tank on different ship types

ZHAO Da-gang*, GUO Chun-yu, KAN Zi

( College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China )

In variable metric series model test, large scale model self-propulsion test, geometric similarity model scale effect test or comparing the test results of different scale towing tank, the blockage effect will be inevitably encountered. When the towing tank scale is small, and the ship model scale is relatively large, the blockage effect is especially prominent. The blockage effect must be corrected, or it will mix among all kinds of analytical results and affect the accuracy of the conclusion. The method of computational fluid dynamics (CFD) is adopted and numerical calculation of the ship resistance for two types of ships under different blockage ratios and speeds is carried out to study the influence of ship form, width and depth of tank on ship resistance. The blockage ratio is changed by changing the size of the computational domain, and the volume of fluid (VOF) method is used to capture the fluid free surface of the ship. In the numerical study, the heaving and pitching motions are considered. Finally, the influence regularity of the blockage effect is obtained, and the reasonable suggestions are put forward for the correction of the blockage effect of the towing tank.

blockage effect; resistance modify; towing tank; multi degree of freedom; computational fluid dynamics (CFD)

2016-04-12；

2016-09-14．

国家自然科学基金资助项目(51379043)；国家自然科学基金青年基金资助项目(51409063).

赵大刚*(1986-)，男，硕士，讲师,E-mail:zhaodagang@hrbeu.edu.cn.

1000-8608(2016)06-0575-09

U661.33

A

10.7511/dllgxb201606004