旋转经常见 解法灵活变

□ 华兴恒

旋转经常见 解法灵活变

□ 华兴恒

旋转是各地中考常见的题型，常常令同学们望而生畏，不知如何入手求解.下面从各地中考试题中选取不同类型的旋转试题进行分析、求解，希望对同学们能够有所启发，克服畏惧心理，提高解题技能.

一、点的旋转

例1（孝感）在平面直角坐标系中，把点P（－5，3）向右平移8个单位得到点P1，再将点P1绕原点旋转90°得到点P2，则点P2的坐标是（ ）.

A.（3，－3） B.（－3，3）

C.（3，3）或（－3，－3）

D.（3，－3）或（－3，3）

解析：点P（－5，3）向右平移8个单位得到的点P1的坐标为（3，3），若点P1绕原点顺时针旋转90°，则对应点P2的坐标为（3，－3）；若点P1绕原点逆时针旋转90°，则对应点P2的坐标为（－3，3）.因此点P2的坐标为（3，－3）或（－3，3），故应选D.

二、直线的旋转

例2（长沙）如图1，在菱形A B C D中，A B＝2，∠A B C＝60°，对角线A C、B D相交于点O，将对角线A C所在的直线绕点O顺时针旋转角α （0°＜α＜90°）后得直线l，直线l与A D、B C两边分别相交于点E和点F.

（1）求证：△A O E≌△C O F；

（2）当α＝30°时，求线段E F的长度.

图1

解析：（1）根据菱形的性质有

A O＝O C，∠O AE＝∠O C F，

又∵ ∠A O E＝∠C O F，

∴ △A O E≌△C O F.

（2）∵ A B＝B C＝2，∠A B C＝60°，

∴ △A B C为等边三角形.

∴ A C＝2，∠A C B＝60°，

此时O C＝1.

∴ 当α＝30°时，O F⊥B C.

在Rt△O F C中，∠C O F＝30°，

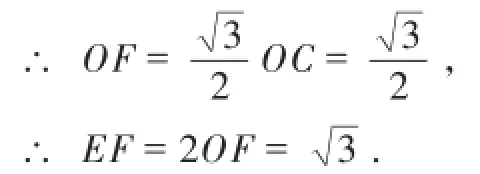
三 角的旋转

例4 （天津）如图2，已知▱A B C D中，A E⊥B C于点E，以点B为中心，取旋转角等于∠A B C，把△B A E顺时针旋转，得到△B A′E′，连接D A′.若∠A D C＝60°，∠AD A′＝50°，则∠D A′E′的大小为（ ）.

A.130° B.150°

C.160° D.170°

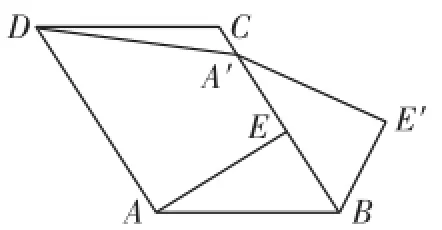
图2

解析：∵ ∠AD C＝60°，

∴ ∠A B C＝60°，

∠D AB＝∠C＝120°，

∴ ∠B A E＝∠B A′E′＝30°，

∠D A′B＝∠A′D C＋∠C

＝10°＋120°＝130°，

∴ ∠D A′E′＝∠D A′B＋∠B A′E′

＝30°＋130°＝160°.

故应选C.

四、三角形的旋转

例4（上海）已知在△ABC中，AB＝AC＝8，∠BAC＝30°.将△ABC绕点A旋转，使点B落在原△ABC的点C处，此时点C落在点D处.延长线段AD，交原三角形的边BC的延长线于点E，那么线段DE的长等于_____.

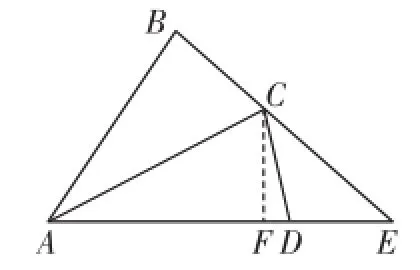
图3

解析：如图3，过点C作C F⊥AD，垂足为点F.

在Rt△A C F中，

A F＝tan∠A C F×C F＝4 3，

∴ D F＝8－4 3.

在△A B E中，∠B A E＝2∠B A C＝60°，∠B＝75°，则∠E＝45°，

∴ E F＝C F＝4，

∴D E＝E F－D F

例5（菏泽）如图4，在平面直角坐标系xO y中，直线y＝ 3 x经过点A，作A B⊥x轴于点B，将△A B O绕点B逆时针转60°得到△C B D.若点B的坐标为（2，0），则点C的坐标为

（ ）.

A.（－1， 3） B.（－2， 3）

C.（-3，1） D.（-3，2）

图4

解析：∵ 点B的坐标为（2，0），A B⊥x轴，

∴ O B＝2，点A的横坐标为2.

∴ 点A的纵坐标为2 3，

∴A B＝2 3.

由旋转的性质得B C＝A B＝2 3，且∠AB C＝60°，

∴ ∠C B O＝90°－∠A B C＝30°.

过点C作C E⊥x轴于点E，

B E＝B C·cos∠C B O

＝2 3·cos30°＝3，

∴O E＝BE－O B＝1，

∴ 点C的坐标为（－1， 3）.

应选A.

五、正方形的旋转

例6（绍兴）正方形A B C D和正方形AE F G有公共顶点A，将正方形A E F G绕点A按顺时针方向旋转，记旋转角∠D A G＝α，其中0°≤α≤ 180°，连接D F、B F，如图5.

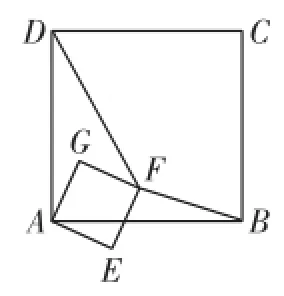
图5

（1）若α＝0°，则D F＝B F，请你加以证明.

（2）试画一个图形（即反例），说明（1）中命题的逆命题是假命题.

（3）对于（1）中命题的逆命题，如果补充一个条件后能使该逆命题为真命题，请直接写出你认为需要补充的一个条件，不必说明理由.

解析：如图6，在正方形A B C D与正方形A E F G中，

∵ G F＝E F，AG＝A E，A D＝A B，

∴ D G＝B E.

又∵ ∠D G F＝∠B E F＝90°，

∴ △D G F≌△B E F，

∴ D F＝B F.

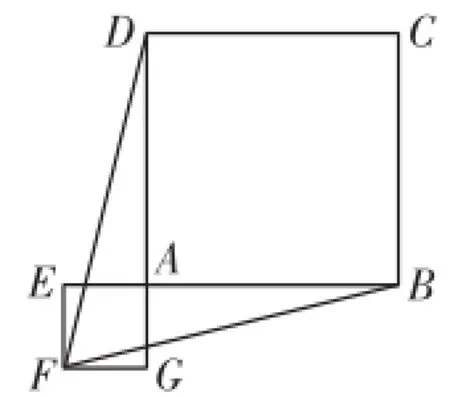
图7

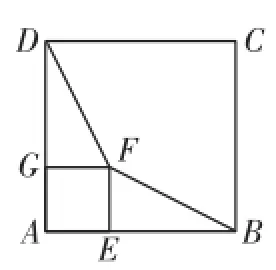
图6

（2）图形（即反例）如图7.

（3）点F在正方形A B C D内或α＜180°.