一题“多变”，提升能力

□ 喻俊鹏

一题“多变”，提升能力

□ 喻俊鹏

有些数学问题通过改变其题设条件或结论，就会变成一个新的问题，虽然它们从表面形式上看不一样，但其实质却是相同的.

例 （人教版九年级数学上册P101页习题24.2第4题）如图1，直线A B经过⊙O上的点C，并且O A＝O B，C A＝C B.求证：直线A B是⊙O的切线.

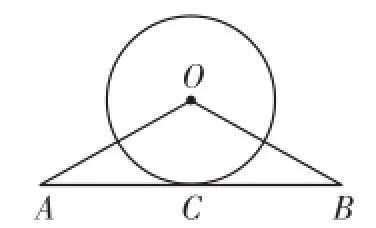
图1

分析：要证明一条直线是圆的切线，通常从两方面去思考：

①若已知直线与圆有公共点，则连接圆心与公共点，构造出一条半径，证明直线垂直于这条半径，根据“经过半径的外端并且垂直于这条半径的直线是圆的切线”，可知该直线是圆的切线，可简记为“连半径，证垂直”.

②若不能确定直线与圆有公共点，则可过圆心作直线的垂线段，然后证明垂线段的长等于圆的半径，根据“圆心到直线的距离等于半径的直线是圆的切线”，可知该直线是圆的切线，可简记为“作垂直，证半径”.

根据上述方法，结合题设条件，易知本题可采用“连半径（O C），证垂直（O C⊥A B）”的方法，证明A B是⊙O的切线.

解题之余，我们可对此问题进

行以下多层次变化探究，以提高分析问题、探究问题与解决问题的能力.

一、改变题设条件

若保证原题结论直线是圆的切线不变（半径与直线垂直），变换问题的条件，就可得到如下的新问题：

变式1 如图2，在Rt△ABO中，∠AOB＝90°，OA＝，OB＝ 25，以O为圆心、4为半径作⊙O，请判断⊙O与直线AB有怎样的位置关系？并说明你的理由.

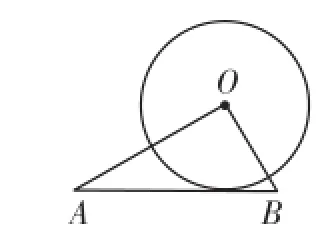
图2

分析：本题中由于改变了题设条件，不能确定直线AB与⊙O是否有公共点，因此需采用方法②，“作垂直，证半径”.即过O点作OC⊥AB（如图3所示），然后通过勾股定理及面积公式得到OC＝4，从而判定直线AB与⊙O相切.

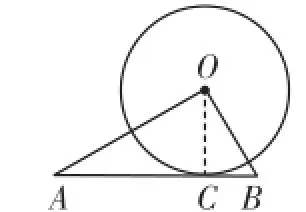
图3

变式2 如图4，直线AB经过⊙O上的点C，OA与⊙O交于点D，若OA＝OB，AD＝CD，∠A＝30°.求证：直线AB是⊙O的切线.

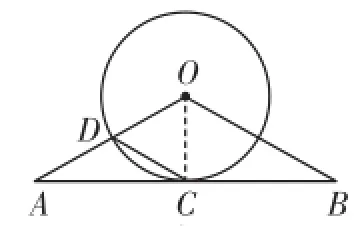
图4

分析：由于已知直线AB经过⊙O上的点C，因此本题可采用方法①，“连半径，证垂直”.即连接OC，利 用 ∠A＝∠ACD＝30°，∠ODC＝∠OCD＝60°，得到∠AOC＝90°，从而证明直线AB是⊙O的切线.

二、条件与结论互换

将问题的结论作为条件，而将某个条件作为结论就可得到以下问题：

变式3 如图5，在△ABC中，OA＝OB，以点O为圆心，作⊙O与边AB相切于点C.求证：AC＝BC.

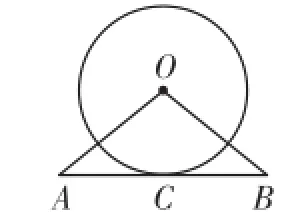
图5

变式4 如图6，点C是△ABC 中AB边的中点，以点O为圆心，作⊙O与边AB相切于点C.求证：OA＝OB.

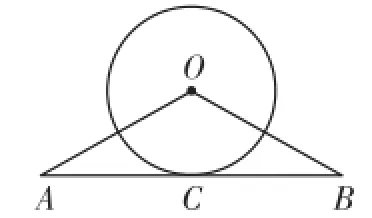
图6

分析：变式3和变式4都是将原题中的结论“AB是⊙O的切线”作为条件，而将某一条件作为要证明的结论.变式3通过连OC，由切线性质及等腰三角形“三线合一”的性质不难得证；而变式4则在连OC后，可由切线及中垂线性质证得.

三、加强条件，拓展结论

我们也可这样思考，在保证原题条件与结论不变的同时，加设问题的条件，延伸出新的结论，这样就可得到如下的问题：

变式5 如图7，在△ABC中，OA＝OB，C是边AB的中点，以O为圆心的圆过点C，且与OA交于点E，与OB交于点F，连接CE、CF.

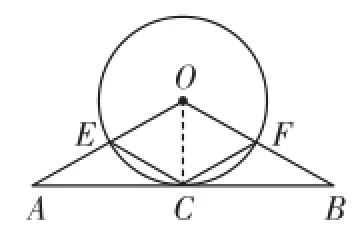
图7

（1）AB是⊙O的切线吗？为什么？

（2）若∠AOB＝∠ECF，试判断四边形OECF的形状，并说明你的理由.

分析：本题的第（1）问实质上与原课本习题完全相同，而第（2）问则通过连接图形中圆上已有的点，形成四边形，对原题图形进行了拓展.

连OC，

易知△EOC≌△FOC（SAS），

得到CE＝CF，

由增加的条件∠AOB＝∠ECF 可 知 ∠EOC＝∠ECO，所 以 CE＝OE＝OF＝CF，从而判断四边形OECF为菱形.

由上可见，问题的条件和结论虽然发生了变化，但其实质（圆中的基本图形及AB是⊙O的切线）并没有发生变化.学习中我们要把握问题的本质，以不变应万变，只有这样，才能不断提升自己的解题能力.