变频电网有源电力滤波器的无源控制策略

高峰， 林辉

(1.西安建筑科技大学 机电工程学院，陕西 西安 710055；2.西北工业大学 自动化学院，陕西 西安 710129)



变频电网有源电力滤波器的无源控制策略

高峰1， 林辉2

(1.西安建筑科技大学 机电工程学院，陕西 西安 710055；2.西北工业大学 自动化学院，陕西 西安 710129)

为了提高变频交流电网的电能质量，针对变频电网有源电力滤波器的复杂工作环境，提出一种基于无源控制理论的具有频率和不确定参数自适应性，带有L2增益的控制策略。该方法首先在考虑了不确定参数、外界干扰和电网频率变化等因素的情况下，建立了非自治有源电力滤波器系统的EL平均化模型。在此基础上，设计了包含不确定参数自适应控制律、L2增益控制律及频率自适应指令电流产生方法的自适应鲁棒控制器，并证明了整个非自治误差伴随系统的稳定性。将提出的方法在变频电网有源电力滤波器系统中进行了仿真验证，并与两种同类典型方法作了比较。理论分析和仿真对比结果表明所提方法在变频电网复杂工况下，能确保并联有源电力滤波器系统的跟踪和补偿效果，而且具有鲁棒性强、频率自适应等优势，具有一定实用价值。

变频电网；有源电力滤波器；无源性；自适应控制；鲁棒性

0 引 言

与恒频交流供电系统相比，变频交流供电系统省去了恒速传动装置或功率变换器，提高了能量转换效率和可靠性。因此，它已成为先进民用大飞机的首选[1]。B-787和A-380的宽变频电网的频率均在360～800 Hz间变化。随着大量机载电子设备(非线性负载)的应用，飞机电网的谐波污染日益严重，带来很大的安全隐患。有源电力滤波器(active power filters，APF)是目前治理谐波污染最有效的工具之一。补偿电流的跟踪性能是保证并联APF补偿性能的关键因素之一。

对于具有本质非线性的APF系统，一些学者先对系统模型局部线性化，再运用成熟的线性控制方法，如PI控制、重复控制等进行控制[2-3]；此方式在特定条件下可取得良好的控制效果，但只能保证在平衡点附近的局部稳定性，当外界干扰较大时，控制效果易变差，甚至不稳定[4]。因此又有学者直接采用非线性方法，如反馈线性化[5]、无源控制等进行控制，取得了较好的效果，可获得全局稳定性。

无源控制(passivity-based control，PBC)是通过“能量整形”和“阻尼注入”的方法，使系统在满足 “无源性”的条件下，渐进稳定于期望平衡点，达到期望的控制性能。其优点是全局定义且全局稳定，无奇异点，鲁棒性强，与系统的物理特性联系紧密[6]。由于电力电子电路的无源性特征,无源控制策略已成为APF控制的研究热点。

文献[7]依据状态空间模型分别设计了单相串、并联APF的无源控制律。文献[8]建立了三相四线四桥臂APF的状态空间模型，并构造了电流无源控制器。文献[9]基于欧拉-拉格朗日(Euler-Lagrange，EL)状态平均模型，提出了带有模糊逻辑推理环节的单相APF无源控制策略，实现了阻尼系数的在线调整。文献[10]建立了系统的端口受控哈密顿模型，并采用互联和阻尼配置无源控制方法, 实现了三相并联混合APF的非线性控制。

为了提高APF无源控制的稳态跟踪精度，文献[11]提出利用重复控制补偿的APF无源性控制方案，提高了系统的稳态跟踪精度。为了应对更复杂的工况，增强系统的适应性和鲁棒性。文献[12]基于EL模型，提出了一种带有参数估计器的三相三线APF的自适应无源控制器，实现了线路参数变化时的准确跟踪。文献[13]依据EL平均化模型，提出了结合H∞控制的三相四线四桥臂APF的无源控制策略，加强了系统的鲁棒性。文献[14]则基于三相三线APF的PCH模型，在文献[12]成果的基础上，加入带有滑动耗散阻尼限幅的L2增益控制，提高了系统对外界干扰的鲁棒性。然而，上述成果的研究对象都是自治系统，当系统的结构参数随时间变化时，如变频电网，系统变为非自治系统，原有控制器的性能将受到影响，稳定性或收敛性需重新检验。对此，文献[15]通过建立系统的时变端口受控哈密顿模型，寻找与时间无关的卡什米尔函数，证明时变系统稳定性，但其无源控制律复杂繁琐，设计难度大。

本文针对变频电网APF系统的结构参数随频率(或时间)变化的特点，建立了非自治APF系统的EL平均化模型。在此基础上，提出一种基于无源控制理论的具有频率、不确定参数自适应性和L2增益的补偿电流控制器，证明了非自治误差伴随系统的稳定性。理论分析和仿真结果表明，所设计的控制器能在频率变化、不确定参数和外界干扰的影响下，保证APF系统的补偿性能。

1 变频电网APF系统的EL平均化模型

图1为变频交流电网并联APF系统结构图。图中APF主电路采用三相四桥臂结构，G1～G8为IGBT。L、Ln为滤波电感，R、Rn等效表示变换器寄生电阻、开关损耗等效电阻和滤波电感电阻成分的综合效应，Vdc为直流侧电容C的端电压，Rc为电容漏电阻。谐波源为三相不可控整流桥接阻感负载(Ld，Rd)，Rm为中线连接电阻。Vsa、Vsb和Vsc分别为电源各相的相电压，ici(i=a,b,c,n)为第i相的补偿电流。定义si代表i桥臂的开关函数，则

(1)

根据KVL和KCL，三相abc静止坐标系下图1系统的数学模型为：

(2)

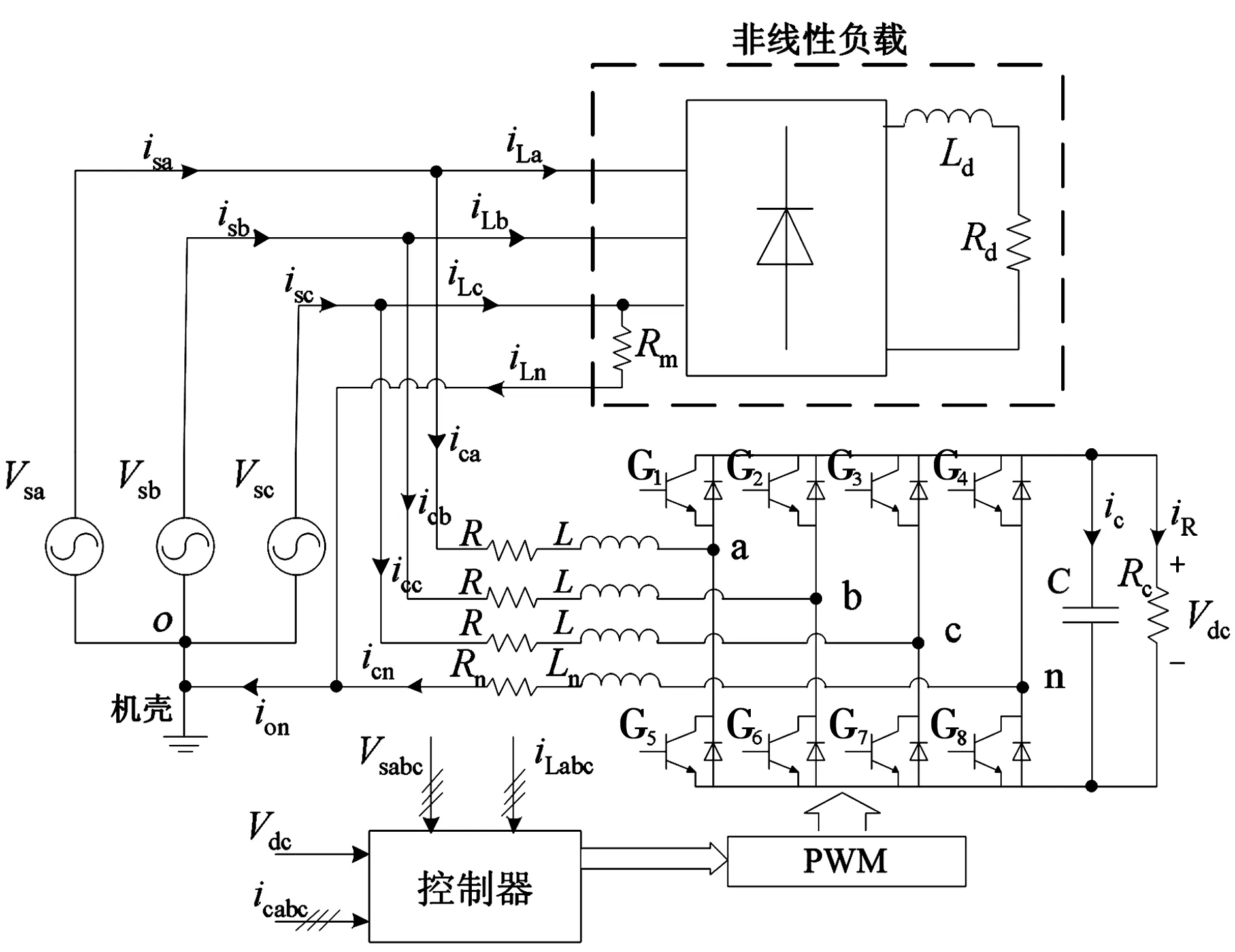
图1 变频电网并联APF系统Fig.1 APF in variable-frequency electric power system

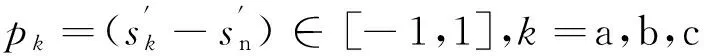
(3)

最后通过式(4)和式(5)的等功率Park变换，即：

[icd,icq,ic0]T=M[ica,icb,icc]T，

(4)

[pd,pq,p0]T=M[pa,pb,pc]T，

(5)

(6)

得到dq0坐标系下的平均化模型为：

(7)

其中：L0=L+3Ln；R0=R+3Rn。定义系统的状态矢量和输入矢量为：

X=[x1,x2,x3,x4]T=[icd,icq,ic0,Vdc]T，

(8)

U=[Vsd,Vsq,Vs0,0]T。

(9)

代入式(7)，整理后得到系统在dq0坐标系下的欧拉-拉格朗日(EL)平均化模型为

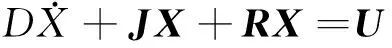
(10)

对于变频电网，发电机由发动机经减速齿轮箱直接驱动，电源频率与发动机转速成正比，因此，时变的转速导致电源角频率也随时间变化(表示为ω(t))。在实际的APF系统中，常存在各种外界干扰，如变换器的死区效应(周期干扰)、负载波动以及器件的理想开关模型与实际过程间的误差等(非周期干扰)，考虑电网频率变化的影响后，可将这些干扰综合表示为

W(t)=[wd(t),wq(t),w0(t),wdc(t)]T。

(11)

其中wi(t)∈L2[0,Tr]，Tr为电网基波周期。

另外，元器件参数的不确定性普遍存在，例如电阻器的阻值会受温度的影响，开关损耗会受随变化频率的影响，电容器的容量也会随着老化缓慢衰减，因此，一些元器件参数很难精确确定。为了简化分析，取R=Rn和L=Ln，则L0=4L，R0=4R。考虑不确定性后的参数转化如表1所示。

表1 原参数及转化参数

注：表中L1，R1，C1，1/Rc1为已知固定常数(经验值)。

未知参数矢量

θ=[θ1,θ2,θ3,θ4]T。

(12)

其中θ1、θ2、θ3和θ4均大于0。

综上所述，在考虑了电网频率变化，外界干扰和参数不确定性后，模型(10)变为

(13)

其中：

(14)

(15)

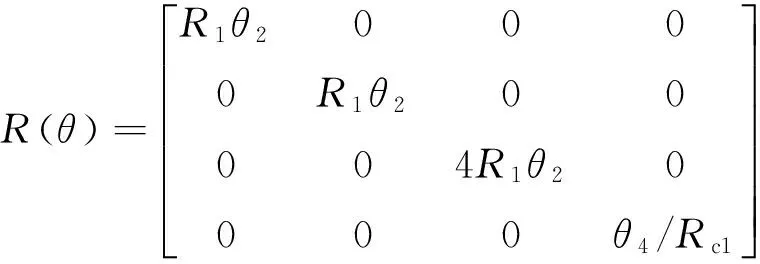
(16)

U(t)=[Vsd(ω(t)),Vsq(ω(t)),Vs0(ω(t)),0]T。

(17)

由于式(11)，式(14)和式(17)中都有时变参数，故式(13)为变频电网APF系统的非自治EL平均化模型。

2 基于PBC方法的自适应鲁棒控制器设计

2.1 误差伴随系统模型

变频电网并联APF系统的控制目标是在频率变化，参数摄动和外界干扰影响下，控制器始终能满足以下两项要求：

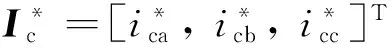
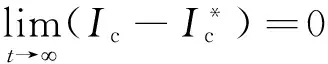
(18)

根据系统控制目标，首先建立APF系统的误差伴随系统。对照式(8)，设系统状态误差矢量Xe= [xe1,xe2,xe3,xe4]T=X-X*=

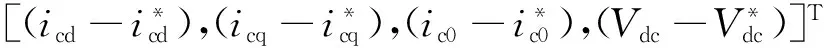
(19)

式中X*为期望状态矢量。则由式(13)和式(19)可推出变频电网APF系统的非自治误差伴随系统模型，即

(20)

其中

(21)

2.2 不确定参数的自适应控制律的设计

为了应对不确定参数的影响，采用自校正方法设计参数自适应控制律，可确保系统在慢变不确定参数影响下也能实现系统的稳定跟踪。设未知参数矢量θ的估计矢量为

(22)

设误差伴随系统(30)的能量存储函数为

(23)

由式(21)和式(22)可得

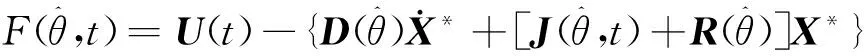
(24)

则能量存储函数(23)的一阶导数为

(25)

(26)

2.3 L2增益控制律的设计

为了抑制外界干扰的影响，采用L2增益控制对外界干扰所造成的跟踪误差进行有效抑制，确保对控制目标的稳定跟踪。

L2增益抑制问题即是在指定的评价信号Z=h(x)的条件下，寻找一个反馈控制律u=β(x)和正定的存储函数V(x)，使得如式(27)所示的γ耗散不等式成立。

(27)

Q(x)为非负定函数，W为干扰矢量，γ为干扰抑制系数且满足γ>0，||·||代表对应矢量的欧几里德范数。在2.2节设计的自适应控制律的基础上，式(25)简化为

(28)

设误差系统输出矢量为

Z=GXe。

(29)

其中G=diag(1,1,1,1)。

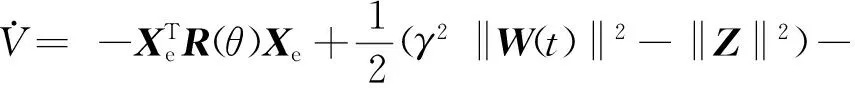
(30)

观察式(30), 若给误差系统加入动态反馈，即

(31)

阻尼系数矩阵K=diag(k1,k2,k3,k4)，k1、k2、k3和k4均大于0。则可得到

(32)

2.4 误差伴随系统稳定性的证明

由于系统(20)为非自治系统，对其的稳定性证明不能再使用LaSalle不变集定理，本文将利用Barbalat引理[17]作“类李雅普诺夫分析”来证明系统(20)的稳定性。

命题1：误差伴随系统(20)渐进稳定。

证明：

1)由前面分析可知，θ1、θ3、L1、C1均大于0。根据式(23)可得

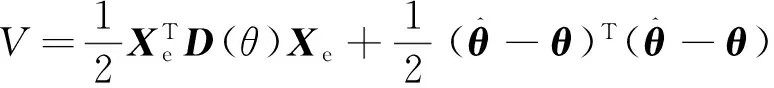
(33)

表明系统的能量存储函数V有下界。

2) 因为wi(t)∈L2[0,Tr]且衰减系数γ∈(0,1)，根据式(32)可得

(34)

上式表明能量存储函数的一阶导数半负定且满足γ耗散不等式。

3)通过式(28)求V的二阶导数可得

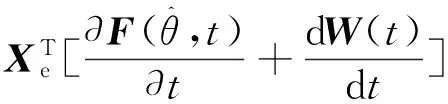
(35)

由于ω(t)，θ，X*均有界，故由式(34)可推出V的二阶导数有界，因此V的一阶导数对时间t一致连续。依据类李雅普诺夫引理[18]可推出

(36)

根据式(16)，式(24)和式(28)可推出

(37)

式(37)表明误差伴随系统渐进稳定于平衡点Xe=0，命题1成立。系统通过L2增益可使干扰W衰减到输出Z。

在2.2，2.3和2.4节设计和证明的基础上，由式(31)可推出系统的自适应L2增益控制律，即：

(38)

图2 基于PBC设计的控制器框图Fig.2 Diagram of designed controller based on PBC

图2为设计的基于PBC方法的自适应鲁棒控制器。控制器可通过锁相环(phase locked loop，PLL)实时采集ω(t)提供给各环节。具有频率自适应的指令电流生成器可依据文献[18]中方法设计。变频条件下，可兼顾指令电流的精度和动态性能。

3 仿真验证及对比

在Matlab/SIMULINK环境下，建立变频电网APF系统的仿真模型。系统参数设置如下：

3.1 不同电源频率时提出方法的控制和补偿效果

提出的控制器参数为：经验值L1=1.2 mH，R1=0.12 Ω，C1=2 050 μF，Rc1=155 kΩ。kp=550，ki=8，γ=0.2，k1=k2=k3=k4=50，K=2πfr。

图5(a)、图5(b)显示了两种频率下，“干扰期”中Isa的频谱和THD值(均小于5%)。可以看出，APF补偿后电源电流满足MIL-STD-704F和IEEE Std.519标准的要求。

图3 fr=360 Hz时提出方法的控制和补偿效果图Fig.3 Control and compensation effects based on proposed method as fr=360 Hz

综上所述，提出的控制器在不确定参数、外界干扰和电网变频等因素的影响下，能较好的完成APF系统的控制目标，补偿效果达到要求。

3.2 提出的方法与其他方法的控制效果比较

由于传统PI控制器受带宽等因素影响，对APF补偿电流控制效果较差[2]，因此在电流内环的控制上，特将提出方法分别与两种基于无源控制的方法进行了比较，以展现提出方法的优势。

图4 fr=700 Hz时提出方法的控制和补偿效果图Fig.4 Control and compensation effects based on proposed method as fr=700 Hz

图5 干扰期中fr=360 Hz和700 Hz时Isa的频谱Fig.5 Spectrum of Isa as fr=360 Hz and fr=700 Hz during interference

3.2.1 与基本的无源控制方法(方法1)[8]的比较

对于给定的APF系统，方法1的电流内环采用基本的无源控制。阻尼系数k1、k2、k3、k4均取为50。电压外环仍采用PI控制，调节后比例和积分系数分别取550和10.5，保证Vdc达到控制目标。

这说明提出方法在受到不确定参数和负载变动干扰时，电流跟踪效果更好，即自适应和L2增益控制的引入提高了无源控制的鲁棒性。

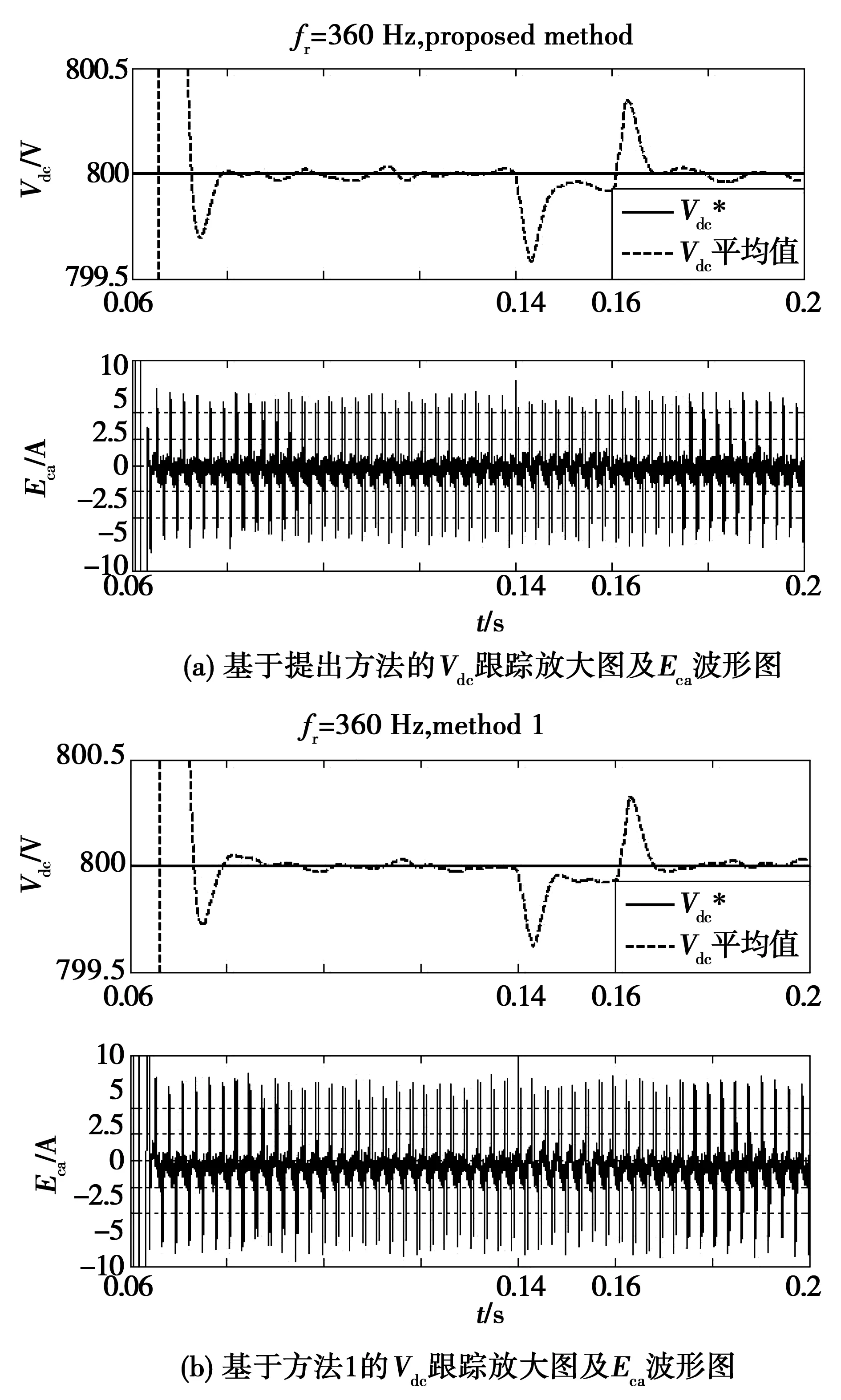
图6 fr=360 Hz时提出方法与方法1控制效果对比图Fig.6 Comparison chart for control effect of proposed method and method 1 as fr=360 Hz

方法|Eca|峰值/A|Eca|平均值/A提出方法7.501.75方法111.202.10

3.2.2 与无频率自适应性的无源控制方法(方法2)[14]的比较

与提出方法不同，方法2未采用自适应指令电流生成器，而是采用含低通滤波器(low pass filter，LPF)的指令电流产生方法。方法2中，阻尼系数取为50，γ=0.2，q1=10，β=0.96，调节后kp=550，ki=5.3，保证Vdc达到控制目标。

图7(a)为fr=360 Hz时“干扰期”中，两种方法得到的A相指令电流IAfpa和电源电流Isa的波形图。图7(b)为fr=700 Hz时“干扰期”刚结束后，两种方法得到IAfpa和Isa的波形图。表3显示了两种方法在不同频率下，得到的IAfpa和Isa的总畸变率和过渡过程周期数。

表3 不同频率时两种方法补偿效果的数值对比

(注：方法2(1)和方法2(2)分别代表采用fc=600 Hz和fc=150 Hz的情况。)

由图7(a)和表3可知，若方法2中指令电流产生单元的LPF选高截止频率fc=600 Hz，当fr下降到360 Hz时，IAfpa的波形畸变明显，其THD已到5.20%，补偿后的Isa也受影响，其THD达到7.22%，不能满足要求。虽然两方法补偿过渡过程等长，但方法2的跟踪精度和补偿效果较差。同样，由图7(b)和表3可知，若选低截止频率fc=150 Hz，当fr上升到700 Hz时，两种方法的补偿效果基本相同，但方法2的IAfpa和Isa的过渡过程比本文方法长约2个周期。说明方法2的补偿速度较慢。以上分析表明，本文方法具有良好的频率自适应能力，能适应变频工况，兼顾电流补偿的精度和快速性。

图7 不同频率时提出方法和方法2补偿效果对比图Fig.7 Comparison chart for compensation effect of proposed method and method 2 at different frequencies

4 结 论

本文依据无源控制理论，提出了一种适用于变频电网环境的控制方法。研究表明：

1)提出的方法在考虑不确定参数和外界干扰的宽变频电网并联APF系统中，能实现控制目标，补偿后电源电流满足相关标准的要求。

2)提出的方法与采用基本无源控制的方法相比，受不确定参数和外界干扰影响时，补偿电流跟踪误差绝对值峰值减小约33%，平均值减小约17%。

3)提出的方法与无频率自适应性的同类方法相比，在电网频率变化时，既能使补偿后电源电流满足要求，同时兼顾了补偿的快速性。

因此，本文提出的方法能够适应变频电网的复杂工况，具有鲁棒性和自适应性强的优势。

[1] CHANG J. Outlook of roles and necessities of power electronics for VF-power system of future large aircraft[C]//International Conference on Electrical Machines and Systems, October 17-20, 2008, Wuhan, China. 2008: 1190-1195.

[2] DANIYAL H, LAM E, BORLE L J, et al. Hysteresis, PI and ramptime current control techniques for APF: an experimental comparison[C]//Industrial Electronics and Applications, June 21-23, 2011, Beijing, China.2011: 2151-2156.

[3] 唐欣，马迎召，李红涛. 基于重复控制的有源滤波器双闭环控制[J]. 电机与控制学报，2009,13(增刊1): 67-71.

TANG Xin, MA Yingzhao, LI Hongtao. Double closed-control of active filter using repetitive algorithm [J]. Electric Machines and Control, 2009,13(Supplement 1): 67-71.

[4] MENDALEK N，AL-HADDAD K，FNAIECH F，et al. Nonlinear control technique to enhance dynamic performance of a shunt active power filter [J]. IEE Proceedings Electric Power Applications, 2003，150(6)：373-379.

[5] 乐江源，谢运祥，张志，等. 三相有源电力滤波器精确反馈线性化空间矢量PWM复合控制[J]. 中国电机工程学报，2010,30(15): 32-39.

LE Jiangyuan，XIE Yunxiang，ZHANG Zhi，et al. Space vector PWM control of three-phase active power filter using exact feedback linearization [J]. Proceedings of the CSEE, 2010, 30(15): 32-39.

[6] ORTEGA R, VAN-DER-SCHAFT A J, MAREELS I, et al. Putting energy back in control [J]. IEEE Control Systems Magazine, 2001, 21(2): 18-33.

[7] RAMIREZ S, VISAIRO N, OLIVER M, et al. Harmonic compensation in the AC mains by the use of current and voltage active filters controlled by a passivity-based law[C]//Power Electronics Congress, October 15-19, 2000, Acapulco, Mexico．2000: 87-92.

[8] 陈菊明，刘锋，梅生伟. 基于无源化方法的三相四线制APF控制器策略[J].电力系统自动化，2006,30(8): 32-36.

CHEN Juming, LIU Feng, MEI Shengwei. Passivity-based controller for three-phase four-wire APF[J]. Automation of Electric Power Systems, 2006,30(8): 32-36.

[9] 张振环，刘会金，李琼林，等. 基于欧拉-拉格朗日模型的单相有源电力滤波器无源性控制新方法[J]. 中国电机工程学报，2008,28(9): 37-44.

ZHANG Zhenhuan, LIU Huijin, LI Qionglin, et al. A novel passivity-based control algorithm for single-phase active power filter using Euler-Lagrange model [J]. Proceedings of the CSEE, 2008,28(9): 37-44.

[10] 鲁伟, 徐长波, 李春文. 并联混合有源滤波器哈密顿系统建模及无源控制[J]. 控制理论及应用，2012，29(11): 1397-1402.

LU Wei, XU Changbo, LI Chunwen. Hamiltonian modeling and passivity-based control of shunt hybrid active power filter [J]. Control Theory & Applications, 2012, 29(11): 1397-1402.

[11] 梁志珊，邱银锋，魏学良. 重复控制补偿的有源电力滤波器无源控制[J]. 电机与控制学报, 2013,17(7): 87-93.

LIANG Zhishan, QIU Yinfeng,WEI Xueliang.Research on passivity-based control of APF with repetitive control compensation [J]. Electric Machines and Control, 2013, 17(7): 87-93.

[12] 薛花，姜建国. 并联型有源滤波器的自适应无源性控制方法研究[J]. 中国电机工程学报，2007,27(25): 114-118.

XUE Hua, JIANG Jianguo. Study on adaptive passivity-based control strategies of shunt active filters[J]. Proceedings of the CSEE, 2007,27(25): 114-118.

[13] CHEN J M, LIU F, MEI S W. Passivity-based H∞ control for APF in three-phase four-wire distribution power systems[C]//Power Engineering Society General Meeting, June 18-22, 2006, Montreal, Canada.2006: 1-6.

[14] 张振环，刘会金，张全明，等. 基于PCH模型的有源电力滤波器滑动耗散阻尼限幅自适应L2增益控制[J].电工技术学报，2008,23(3)：80-91.

ZHANG Zhenhuan, LIU Huijin, ZHANG Quanming, et al. A novel adaptiveL2gain control algorithm with sliding dissipative damping and limitation for active power filter based on PCH model [J]. Transactions of China Electrotechnical Society, 2008,23(3): 80-91.

[15] WANG Y Z, CHENG D Z, HU X M. Problems on time-varying port-controlled Hamiltonian systems: geometric structure and dissipative realization [J]. Automatica, 2005,41(4): 717-723.

[16] ESCOBAR G, STANKOVIC A M, MATTAVELLI P. An adaptive controller in stationary reference frame for D-statcom in unbalanced operation [J]. IEEE Transaction on Industrial Electronics, 2004,51(2):401-409.

[17] JEAN-JACQUES S, WEIPING L. Applied nonlinear control [M]. New Jersey: Prentice Hall, 1991: 122-126.

[18] 高峰，林辉. 三相四线制变频电网的谐波及无功电流检测[J].电机与控制学报，2014,18(10): 14-20.

GAO Feng, LIN Hui. Detection for harmonics and reactive currents in three-phase four-wire variable-frequency power system [J]. Electric Machines and Control, 2014,18(10): 14-20.

(编辑：刘琳琳)

Passivity control strategies of active power filters in variable-frequency power system

GAO Feng1， LIN Hui2

(1. School of Mechanical and Electrical Engineering, Xi'an University of Architecture and Technology, Xi’an 710055, China; 2.School of Automation, Northwestern Polytechnical University, Xi’an 710129, China)

To improve power quality of variable-frequency power system and adapt to the complex working environment of active power filters(APF), a novel control strategy based on passivity theory withL2gain and the adaptabilities for frequency and uncertain parameters was proposed. A non-autonomous Euler-Lagrange (EL) averaged model of APF considering uncertain parameters, outside interferences and varying frequency was built.Then an adaptive robust controller which consists of adaptive control law for uncertain parameters,L2gain control law for outside interferences and adaptive reference current generating method for grid frequency was designed and the stability of the non-autonomous error adjoint system was proved. The simulation results from proposed controller and another two controllers were compared. Theory analysis and simulation comparisons were presented to verify the validity and superiority in robustness and frequency adaptability of the proposed controller in variable-frequency power system.

variable-frequency power system; active power filters; passivity; adaptive control; robustness

2013-12-04

陕西省教育厅专项科研计划项目(16JK1451); 西安建筑科技大学基础研究基金(JC1512); 西安建筑科技大学人才科技基金(RC1424)

高 峰(1975—)，男，博士，讲师，研究方向为电力电子功率变换、电能质量控制、新能源发电技术;

林 辉(1957—)，男，博士，教授，博士生导师，研究方向为电机控制、迭代控制理论研究。

高 峰

10.15938/j.emc.2016.11.009

TM 71

A

1007-449X(2016)11-0061-09