高阶SVD和全变差正则的乘性噪声去除模型
2016-12-07霍雷刚冯象初王旭东霍春雷
霍雷刚,冯象初,王旭东,霍春雷
(1.西安电子科技大学数学与统计学院,陕西西安 710071;2.广西师范学院计算机与信息工程学院,广西南宁 530023;3.中国科学院自动化研究所模式识别国家重点实验室,北京 100080)
高阶SVD和全变差正则的乘性噪声去除模型
霍雷刚1,冯象初1,王旭东2,霍春雷3
(1.西安电子科技大学数学与统计学院,陕西西安 710071;2.广西师范学院计算机与信息工程学院,广西南宁 530023;3.中国科学院自动化研究所模式识别国家重点实验室,北京 100080)
光滑性、稀疏性和自相似性先验作为自然图像的重要特性被广泛应用于图像去噪.根据高阶奇异值分解和全变差正则的互补性,提出了一种能够同时利用光滑性、稀疏性和自相似性先验的乘性噪声去除新方法.该方法首先采用高阶奇异值分解方法对对数变换后图像中的相似块组进行去噪;然后结合考虑光滑性先验的全变差约束对结果进行迭代优化.实验结果表明,该方法在有效去除乘性噪声的同时,可以更好地保留图像的边缘和纹理区域的细节信息.
高阶奇异值分解;乘性噪声;全变差;非局部滤波;图像去噪
乘性噪声是一种广泛存在于核磁共振、遥感、合成孔径雷达等成像领域的噪声[1-14].乘性噪声的存在降低了图像的画面质量,严重地影响图像的分割、分类、目标检测、感兴趣区域提取等后续的应用.因此,研究和发展含乘性噪声图像的恢复方法具有重要的理论意义和应用价值.然而,相对于加性高斯白噪声,乘性噪声更复杂,传统的基于高斯分布假设的去加性噪声模型不能直接用于去除乘性噪声.
含乘性噪声图像的恢复是一个不适定问题,需要通过添加关于图像和噪声的先验约束将其转变为适定问题.目前,图像主要采用3种形式的先验[15-17],即全局正则性先验[18]、稀疏性先验[19]和自相似性先验[20-22].对于噪声的先验,近年来,采用伽马分布模拟乘性噪声的方法得到广泛关注和发展[1-14,23].去除乘性伽马噪声的方法可以分为两大类在乘性噪声满足伽马分布假设和最大后验概率估计框架下,利用先验约束对待恢复图像建立合适的能量泛函,通过变分法将优化问题转化为全变差(TotalVariation,TV)或高阶全变差求解[1-2,4,6,13-14],或者利用对偶求解其分裂形式[3,5],或者转化为滤波形式[7]进行求解利用对数变换将去乘性噪声问题转化为去加性噪声问题,将对数域图像在框架(例如,小波基)下的分解系数进行阈值处理,对阈值处理后的系数进行重构,然后进行指数变换得到恢复图像[8-10].
上述现有去乘性噪声的方法大都只利用了一种或两种图像先验.例如,基于变分的方法[1-6,12-14]一般采用光滑性先验;基于多尺度框架和阈值收缩算法的DFN模型[8]和HMNZ模型[10]结合了稀疏性和光滑性先验;非局部滤波方法[7]只利用自相似性先验.针对上述缺陷,笔者提出了基于高阶奇异值分解(HigherOrder SingularValueDecomposition,HOSVD)和全变差正则的去乘性噪声模型,综合利用了3种先验.
1 高阶奇异值分解和全变差正则的去乘性噪声模型
先介绍乘性噪声的数学表示和已有的HMNZ模型[10],在此基础上详细叙述提出的新模型.
笔者考虑的乘性噪声为

其中,x=(x1,x2),表示图像所在二维区域Ω⊂R2上的点;f(x),u(x),v(x):ΩaR+,分别对应观测图像、待恢复图像和噪声图像在给定x点处的像素值.假定v(x)对于所有的x∈Ω是相互独立的,并服从均值为1的伽马分布,相应的概率密度函数为

其中,Γ(·)为伽马函数,伽马分布的方差为1/L;L表示噪声强度.
对式(1)两边取对数,并记z(x)=logf(x),y(x)=logu(x),ε(x)=logv(x),则有z(x)=y(x)+ε(x),从而,乘性噪声问题转化为加性噪声问题.当L足够大时,噪声ε的分布可近似为均值为零、标准差为σ(σ=的高斯分布[9,11],其中,Ψl(L)=(ddL)l+1logΓ(L),l={0,1}.利用噪声的这种特性,可以很容易地将去加性噪声的方法用于去除乘性噪声[3,9].
假设图像的大小为N×N,则图像中存在(N-n+1)2个大小为n×n的重叠选取的图像块,将这些图像块的左上角的坐标集合用索引值表示为I={1,2,…,i,…,(N-n+1)2}.F∈RN×N,U∈RN×N,V∈RN×N,分别表示观测图像、待恢复图像和噪声,f∈RN2,u∈RN2,v∈RN2,分别为F,U,V的列向量表示. Ci(U)∈Rn×n,表示从U中抽取的第i个图像块,将其表示成列向量的形式为,这里是由大小为n2×N2的矩阵表示的线性算子,该矩阵的每一行只有一个元素为1且其余元素均为零.
文中,向量和矩阵的内积统一用<·,·>表示,logu(logU)表示对向量u(矩阵U)的每个元素分别取对数,·/·表示向量或矩阵的对应元素分别相除.1N表示N维的全1向量,1N×N表示大小为N×N的全1矩阵.表示图像U的全变差,特别地,表示列向量u对应的二维图像的全变差.
HMNZ模型[10]对应的能量泛函的一般形式为

其中,第1项是似然项,第2项对应对数域图像的光滑约束,最后一项是对对数域图像中图像块的约束;λ,γ是正则化参数;,是与图像块Ci(logu)有关的函数,其中的μi是正则化参数;D表示冗余字典,采用K奇异值分解(K-SingularValueDecomposition,K-SVD)算法[19]求解;αi表示在字典下的表示系数,是对表示系数的稀疏约束.HMNZ模型存在以下不足:①所有图像块共用一个字典,未充分考虑字典的局部自适应性;②将图像块排列成列向量,不能很好地保持图像块的二维结构;③对每个图像块的稀疏表示单独求解,对块与块之间的相关性考虑不足.换句话说,没有利用图像块的自相似性.
考虑图像块相似性的算法可以取得更好的去噪效果[15-17,21-22].这类算法的基础是对相似块组整体结构的先验假定.例如,三维块匹配滤波(Block-Matching and 3D filtering,BM3D)模型[21]利用三维逼近对每一个相似块组进行去噪;高阶奇异值分解模型[22]对每一个相似块组在局部自适应变换基下进行稀疏表示.受此启发,笔者提出利用相似块组先验的去乘性噪声模型,其一般形式可以写成

其中,θi为正则化参数;Gi(log U)表示与第i个图像块相似的一组图像块,若该相似块组中图像块的个数为Ki,则对应的张量表示为Ti=Gi(log U)∈Rn×n×Ki;ψ表示对相似块组的先验约束.当θi=1(i∈I)且每个相似块组中的图像块个数均为1时,式(4)退化为式(3),因此,式(4)是式(3)的自然推广.
以高阶奇异值分解模型[22]作为相似块组的先验.定义

其中,×m(m=1,2,3)表示模m张量积;列正交的因子矩阵,分别由张量Ti=Gi(log U)的模m(m=1,2,3)展开矩阵的奇异值分解得到;核心张量Si∈Rn×n×Ki,表示对应的展开系数,是对系数的稀疏约束.
与K奇异值分解算法[19]相比,高阶奇异值分解模型[22]具有以下优势:①将图像块的稀疏表示扩展至相似块组的稀疏表示,并且采用的变换基是局部自适应的;②不需要将图像块排成列向量,保持了图像块的二维结构;③采用三维变换基,考虑了相似块组的行与行、列与列以及块与块之间的相关性;④对构成相似块组的每一个图像块进行去噪,保持了相似块组的整体结构.换句话说,高阶奇异值分解模型[22]综合了局部自适应性、稀疏性、自相似性,保持了图像块的二维结构.综上,采用高阶奇异值分解模型可以弥补基于K奇异值分解算法的HMNZ模型[10]的不足.将式(5)对相似块组的约束带入到式(4)的一般形式中,得出笔者建立的模型:
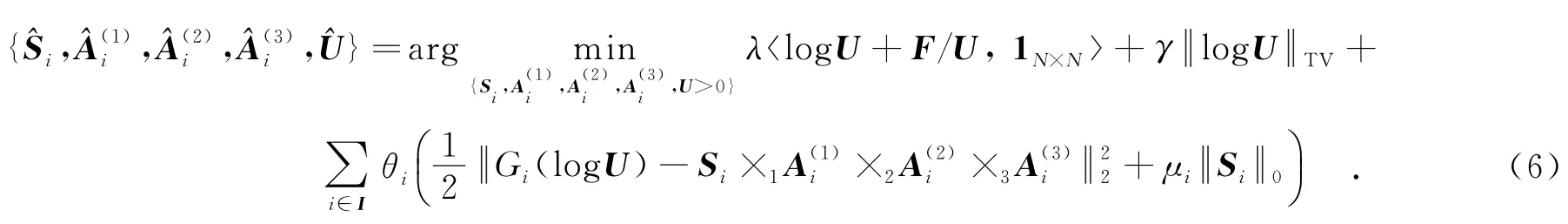
2 模型求解
与文献[10,19]类似,采用两步法求解式(6)对应的最小化问题:
下面对上述两步分别进行描述.
2.1自适应变换基学习和相似块组去噪
高阶奇异值分解模型[22]对相似块组进行去噪的步骤如下:①对含噪声的对数域图像Z=log F中的每一个图像块,由其在局部邻域内的相似块构造相似块组;②对每一个相似块组构成的张量进行高阶奇异值分解,得到数据自适应的三维变换基和在该基下的展开系数Si; ③对展开系数的稀疏约束可以通过硬阈值处理求解,即将Si中幅值小于全局阈值τ=σ(2 log(n×n×Ki))1/2的元素置零,其他元素保持不变,得到阈值后的展开系数i;进行高阶奇异值分解的反变换,得到去噪后的相似块组i=
2.2松弛问题求解
得到每个相似块组的去噪结果后,式(6)可以转化为如下的松弛问题:

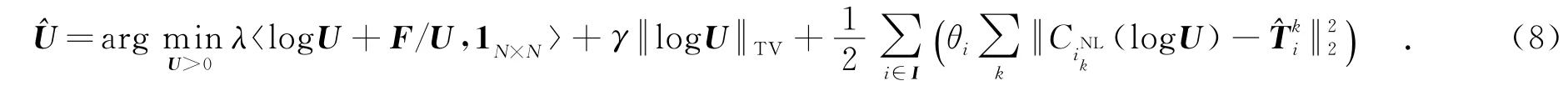
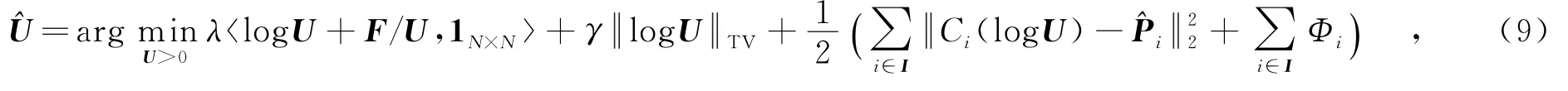
其中,Φi是与{Ci(log U)}无关的量.
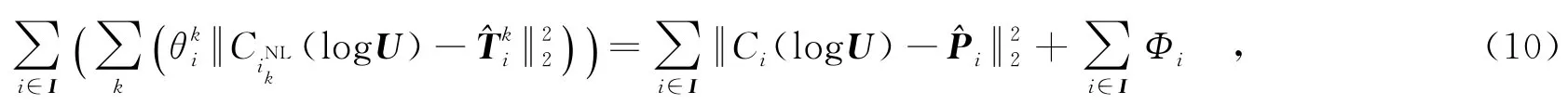
其中,Φi与{Ci(log U)}无关.

即Φc与{Ci(log U)}无关.证毕.
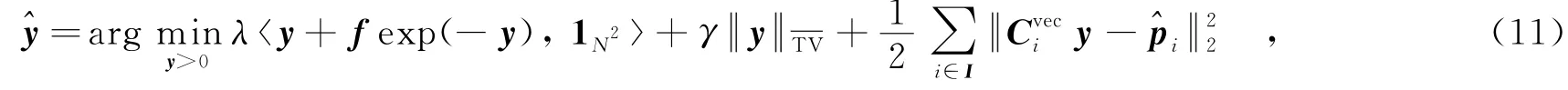
其中,指数乘法表示对应元素相乘.上式可以采用文献[10]给出的Chambolle-Pock对偶算法进行求解.
此外,在对数变换过程中,会产生一个偏差,因此从对数域中的估计信号得到最终去噪图像时须进行偏差矫正.笔者文选用文献[23]的矫正方式,即=exp()ex( p log L-Ψ0(L)).
综上所述,基于文中模型的乘性噪声去除算法如下:
步骤1 对含乘性噪声图像进行对数变换,得到对数域图像;
步骤2 估计对数域图像的噪声标准差σ,采用高阶奇异值分解模型对每个相似块组进行去噪;
步骤3 利用Chambolle-Pock对偶算法迭代求解松弛问题式(11),得到去噪后的对数域图像;
根据文献[22],利用维纳滤波可以进一步提升去噪效果,由于篇幅限制,这里不再赘述。由此,笔者提出的算法可以有两种具体实现,为了加以区分,将对相似块组去噪时不加维纳滤波步骤的算法记为TVHOSVD1,将添加维纳滤波步骤的算法记为TV-HOSVD2.
3 数值实验
为了验证提出模型和算法的有效性,本节给出了不同模型和算法在4幅图像(Cameraman,Peppers,Barbara大小为256×256;Nîmes大小为512×512)分别受到均值为1、不同强度(L={4,10})的伽马噪声污染图像的去噪结果.采用平均绝对值误差(Mean Absolute-deviation Error,MAE)EMAE、峰值信噪比(Peak Signal to Noise Ratio,PSNR)RPSNR这两个指标对去噪结果进行客观评价,分别定义如下:
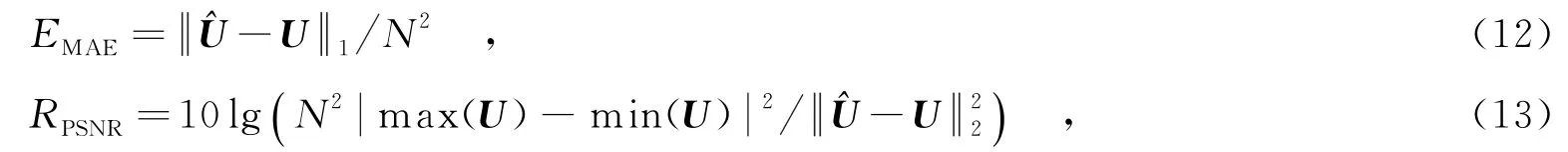
对于对比模型,按照文献[10]的方法调整模型中的参数,使其对应的客观评价指标达到最优.对于笔者提出的模型,所有实验采用相同的参数:相似块组去噪步骤选用文献[22]给出的参数,即图像块的大小为8×8,非局部相似块的搜索半径为20;相似性标准为,其中Pref为参考块,Pi为相似块,每个相似块组中的图像块个数小于等于30;正则化参数λ=0.3/σ,β=10,γ=2,牛顿法迭代次数为5;对偶算法最大迭代次数为500;当相邻两次迭代恢复的对数域图像的相对误差小于等于2.5×10-10时,停止迭代.经过多次测试,采用以上参数可以取得很好的效果.
3.1客观评价
选取4种已有去噪模型的客观评价结果进行对比,分别为AA模型[1]、DFN模型[8]、TL模型[7]和HMNZ模型[10].表1列出了笔者提出的模型的两种算法和对比模型在4幅图像上的峰值信噪比和平均绝对值误差指标,可以看出,新模型的两种算法均达到了更高的峰值信噪比和更低(或相当)的平均绝对值误差.以L=10时的Cameraman图像为例,与含噪声图像相比,4种对比模型的峰值信噪比分别提高8.82 dB,10.42 d B,10.89 d B,11.66 dB,笔者提出的模型的两种算法分别提高11.78 d B,11.9 d B;对应的平均绝对值误差分别降低19.49,21.99,22.57,22.76,笔者提出的模型的两种算法分别降低22.69,22.62.对比笔者提出的模型两个算法的结果还可以看出,对于纹理较丰富的图像,增加维纳滤波后去噪效果得到进一步提升.例如,Barbara在L=10和L=4时,增加维纳滤波步骤前后峰值信噪比分别提高0.48 d B和0.09 dB,平均绝对值误差分别降低0.38和0.06.

表1 4个测试图像去噪结果的客观评价指标
3.2主观评价
图1列出了Barbara和Cameraman图像在噪声强度较大(L=4)时的去噪结果.对结果进行分析如下.

图1 图像去噪结果(L=4,第1行对应Barbara,第2行对应Cameraman局部)
(1)纹理的保留和模糊的去除:对比图1第1行Barbara图像的纹理区域(如右上角的窗帘和左下的围巾处),可以看出,笔者提出的模型较好地保留了纹理细节;对比该行平滑区域(如脸部),可以看出,DFN模型出现块效应和虚假边缘,HMNZ模型出现边缘模糊,笔者提出的模型有效地降低了模糊现象,特别是人物的眼睛部位.
(2)边缘的保留:图1第2行是Cameraman图像中相机支架和远处建筑部位的局部放大图像,可以看出,DFN模型存在块效应和边缘丢失,HMNZ模型过平滑以致中间的支架丢失,笔者提出的模型边缘保留得较好.
4 总 结
基于高阶奇异值分解和全变差正则,笔者提出了利用相似块组约束的去乘性噪声模型,给出了数值求解方法.该模型综合利用了光滑性、稀疏性和自相似性3种图像先验.与传统的方法相比,新模型在有效去除噪声和块效应的同时,较好地保留了图像边缘和纹理区域的细节信息.
[1]AUBERT G,AUJOL J.A Variational Approach to Removing Multiplicative Noise[J].SIAM Journal on Applied Mathematics,2008,68(4):925-946.
[2]JIN Z M,YANG X P.Analysis of a New Variation Model for Multiplicative Noise Removal[J].Journal of Mathematical Analysis and Applications,2010,36(2):415-426.
[3]HUANG Y M,NG M K,WEN Y W.A New Total Variation Method for Multiplicative Noise Removal[J].SIAM Journal on Imaging Sciences,2009,2(1):20-40.
[4]王旭东,冯象初,霍雷刚.去除乘性噪声的重加权各向异性全变差模型[J].自动化学报,2012,38(3):444-451. WANG Xudong,FENG Xiangchu,HUO Leigang.Iteratively Reweighted Anisotropic-TV Based Multiplicative Noise Removal Model[J].Acta Automatica Sinica,2012,38(3):444-451.
[5]王旭东,冯象初,张选德.去除乘性噪声的迭代重加权二阶正则模型[J].西安电子科技大学学报,2014,41(2):130-136. WANG Xudong,FENG Xiangchu,ZHANG Xuande.Iteratively Reweighted Second-order Regularization Based Multiplicative Noise Removal Model[J].Journal of Xidian University,2014,41(2):130-136.
[6]白键,冯象初.去除乘性噪声的积分微分方程模型[J].西安电子科技大学学报,2013,40(3):132-138. BAI Jian,FENG Xiangchu.Model Based on the Integro-differential Equation for Multiplicative Noise Removal[J]. Journal of Xidian University,2013,40(3):132-138.
[7]TEUBER T,LANG A.Nonlocal Filters for Removing Multiplicative Noise[C]//Scale Space and Variational Methods: 6667.New York:Springer-Verlag,2012:56-61.
[8]DURAND S,FADILI J,NIKOLOVA M.Multiplicative Noise Removal Using L1Fidelity on Frame Coefficients[J]. Journal of Mathematical Imaging and Vision,2010,36(3):201-226.
[9]姚莉丽,冯象初,李亚峰.去除乘性噪音的主成分分析算法[J].光子学报,2011,40(7):1031-1035. YAO Lili,FENG Xiangchu,LI Yafeng.Principal Component Analysis Method for Multiplicative Noise Removal[J]. Acta Photonica Sinica,2011,40(7):1031-1035.
[10]HUANG Y M,MOISAN L,NG M K,et al.Multiplicative Noise Removal via a Learned Dictionary[J].IEEE Transactions on Image Processing,2012,21(11):4534-4543.
[11]XIE H,PIERCE L E,ULABY F T.Statistical Properties of Logarithmically Transformed Speckle[J].IEEE Transactions on Geoscience and Remote Sensing,2002,40(3):721-727.
[12]LIU C,ZHU S.A Convex Relaxation Method for Computing Exact Global Solutions for Multiplicative Noise Removal [J].Journal of Computational and Applied Mathematics,2013,238:144-155.
[13]BINI A A,BHAT M S.A Fourth-order Partial Differential Equation Model for Multiplicative Noise Removal in Images [C]//Proceedings of Emerging Trends in Communication,Control,Signal Processing&Computing Applications. Piscataway:IEEE,2013:1-5.
[14]HAN Y,XU C,BACIU G,et al.Multiplicative Noise Removal Combining a Total Variation Regularizer and a Nonconvex Regularizer[J].International Journal of Computer Mathematics,2014,91(10):2243-2259.
[15]ZHANG X D,FENG X C,WANG W W.Two-direction Nonlocal Model for Image Denoising[J].IEEE Transactions on Image Processing,2013,22(1):408-412.
[16]ZHANG X D,FENG X C,WANG W W.Two-direction Nonlocal Model for Image Interpolation[J].Science China Technological Sciences,2013,56(4):930-939.
[17]ZHANG X D,FENG X C,WANG W W.Image Denoising via 2D Dictionary Learning and Adaptive Hard Thresholding [J].Pattern Recognition Letters,2013,34(16):2110-2117.
[18]RUDIN L,OSHER S,FATEMI E.Nonlinear Total Variation Based Noise Removal Algorithms[J].Physica D,1992,60:259-268.
[19]ELAD M,AHARON M.Image Denoising via Sparse and Redundant Representation over Learned Dictionaries[J]. IEEE Transactions on Image Processing,2006,15(12):3736-3745.
[20]BUADES A,COLL B,MOREL J M.A Nonlocal Algorithm for Image Denoising[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition:2.Los Alamitos:IEEE Computer Society,2005: 60-65.
[21]DABOV K,FOI A,KATKOVNIK V,et al.Image Denoising by Sparse 3D Transform-domain Collaborative Filtering [J].IEEE Transactions on Image Processing,2007,16(8):2080-2095.
[22]RAJWADE A,RANGARAJAN A,BANERJEE A.Image Denoising Using The Higher Order Singular Value Decomposition [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(4):849-862.
[23]XIE H,PIERCE L E,ULABY F T.SAR Speckle Reduction Using Wavelet Denoising and Markov Random Field Modeling[J].IEEE Transactions on Geoscience and Remote Sensing,2002,40(10):2196-2212.
(编辑:郭 华)
Higherorder singular value decomposition-and total variation-regularized multiplicative noise removal model
HUO Leigang1,FENG Xiangchu1,WANG Xudong2,HUO Chunlei3
(1.School of Mathematics and Statistics,Xidian Univ.,Xi’an 710071,China;2.School of Computer and Information Engineering,Guangxi Teachers Education Univ.,Nanning 530023,China;3.NLPR,Institute of Automation,Chinese Academy of Sciences,Beijing 100080)
Smoothness,sparsity and self-similarity are the priors widely used in image denoising due to their importance in representing natural images.Motivated by the collaborative roles of higher order singular value decomposition and total variation regularization,a new approach that can simultaneously capture the above priors is proposed in this paper for removing the multiplicative noises.By taking advantages of local adaptiveness,sparsity and self-similarity realized by higher order singular value decomposition,the proposed approach starts with similar-patch-group-wise adaptive denoising on the logtransformed image,followed by the iterative optimization implemented by the total variation constraint which considers the prior of smoothness.Experiments demonstrate the advantages of the proposed approach in removing multiplicative noise and preserving the details near the edges and in the texture area.
higher order singular value decomposition;multiplicative noise;total variation;nonlocal filter;image denoising
O175.2;TN911.7
A
1001-2400(2016)03-0078-07
10.3969/j.issn.1001-2400.2016.03.014
2015-03-19
时间:2015-07-27
国家自然科学基金资助项目(61271294,61472303,61362029,61379030);中央高校基本科研业务费专项资金资助项目(NSIY21)
霍雷刚(1986-),男,西安电子科技大学博士研究生,E-mail:leiganghuo@163.com.
http://www.cnki.net/kcms/detail/61.1076.TN.20150727.1952.014.html
