无限最大间隔Beta过程因子分析模型
2016-12-07张学峰王鹏辉刘宏伟
张学峰,陈 渤,王鹏辉,文 伟,刘宏伟
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)
无限最大间隔Beta过程因子分析模型
张学峰,陈 渤,王鹏辉,文 伟,刘宏伟
(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)
针对多模分布数据的分类问题,文中提出了一种无限最大间隔Beta过程因子分析模型.该模型利用Beta过程因子分析模型挖掘数据低维的隐含信息.同时借鉴混合专家思想,采用Dirichlet混合模型将数据在隐空间划分成“无限”个子集,并在每个子集上训练一个线性的最大间隔分类器实现全局非线性的复杂分类器.由于将数据降维、子集划分以及分类器统一在贝叶斯框架下,文中模型在充分挖掘数据结构的同时保证数据的可分性.文中采用非参数贝叶斯技术避免了模型选择问题,利用Gibbs采样技术简便有效地估计了模型参数.基于公共数据集和实测雷达高分辨距离像数据的实验验证了文中方法的有效性.
Beta过程因子分析模型;混合专家;Dirichlet混合模型;最大间隔分类器
因子分析(Factor Analysis,FA)模型是一种生成模型,可以描述数据在低维隐空间的信息[1-3].在分类任务中,FA模型常被用于数据的降维、特征提取以及概率分布描述.然而,在这些应用中没有利用对分类有益的类别信息.与之相对的,判别模型则通常在最小分类误差的约束下,用带有类别信息的训练样本来训练分类器,并将样本映射到其对应的类别.判别模型相比于生成模型具有更好的分类能力,而生成模型则具有更好的数据描述能力,可以挖掘数据内在的信息.因此,可以将FA模型与判别模型相结合,以期得到具有良好可分性的低维隐空间特征,从而在保留FA模型对数据描述能力的同时提升其分类性能.
支撑向量机(Support Vector Machine,SVM)是人们最为熟知的判别模型[4],它是一种最大间隔分类器,具有良好的分类和推广性能.然而,传统SVM模型中的最大间隔约束难以应用于概率框架.文献[5]开发了一种隐变量SVM(Latent Variable representation for SVMs,LVSVM)模型.该模型通过引入隐变量,将SVM的优化准则表达为条件高斯线性模型,从而可以将SVM与概率模型有机地结合在一起.
现有的一些研究也采用了将生成模型与判决模型(特别是SVM)相结合来提高模型分类性能的思想.在文献[6-7]中,研究者将SVM引入隐含Dirichlet分配(Latent Dirichlet Allocation,LDA)模型.其中文献[7]采用了LVSVM,从而将整个最大间隔主题模型统一在概率框架下,进而可以采用Gibbs采样技术[8]对模型参数进行简单有效的估计.文献[9]将线性分类器与隐变量模型相结合提出了ILSVM(Infinite Latent SVM)模型.模型中利用非参数贝叶斯先验来确定隐变量个数,解决了模型选择问题.然而,该模型隐变量为二值变量,这限制了其分类性能.以上这些方法均为线性模型,不能处理复杂数据.
对于具有多模结构的数据,采用单一的分类器进行分类,一方面会增加分类器的设计复杂度,另一方面会忽略数据的内在结构而不利于分类.文献[10-12]中的模型均为无限混合专家模型,在利用Dirichlet过程(Dirichlet Process,DP)混合模型将数据划分为“无限”个子集的同时,在每个子集上训练一个简单的线性分类器,以解决全局非线性分类问题.与传统方法相比,该类方法既不用预先确定子集个数,又可以将子集划分与后端的分类任务相结合,保证了各个子集的可分性,提高了全局分类性能.
笔者将无限混合专家思想引入到FA模型中,在充分挖掘数据的隐含结构的同时,在隐空间采用多个简单的分类器实现非线性分类.具体地,采用FA模型对数据在隐空间(特征空间)描述,同时利用DP混合模型将特征空间划分为“无限”个子集,并且在每个子集上学习一个LVSVM分类器.为了解决FA的因子个数选择(即模型选择)问题,文中采用Beta过程因子分析(Beta Process Factor Analysis,BPFA)模型[13],该模型将Beta过程(Beta Process,BP)先验引入FA模型来自动选择因子个数.因而,文中将整个模型称为无限最大间隔Beta过程因子分析(Infinite Max-Margin BPFA,IMMBPFA)模型.IMMBPFA模型将数据表达、子集划分及分类器联合学习,一定程度上使得各个子集中样本分布一致且线性可分.由于采用LVSVM作为分类器,整个模型是全共轭的,可以利用Bayesian估计方法对参数进行简单有效的估计.与文献[11-12]中的模型相比,该模型是在特征空间进行子集划分和分类器学习的,更加灵活且可以降低冗余信息对分类性能的影响.基于公共数据集和实测数据的实验结果表明,文中模型可以在避免模型选择问题的同时有效提高分类性能.
1 Beta过程因子分析模型
因子分析(FA)模型是一种常用的概率隐空间模型,它将观测数据映射到由一组基构成的子空间中,并用隐变量表征数据的隐空间特征.FA假设P维观测样本x是由一个K(K FA模型对数据描述时,其因子个数K是未知的,且需要预先设置.如果设置得过大或者过小会引起模型的过匹配或者欠匹配.为了解决该模型选择问题,文献[13]利用非参数贝叶斯技术,将Beta过程引入FA模型,提出了BPFA模型,该模型可以根据数据自动确定所需因子个数.BPFA模型的结构为 2.1隐变量SVM模型 其中,γ称为调和参数,为正常数. 由此可以将LVSVM与概率生成模型(如FA等)进行有机结合,从而将监督信息引入到这些模型中,增强其分类性能[7,11].另外,SVM为两类分类器,在处理多类问题时可以采用一对多策略[4]进行扩展. 2.2最大间隔Dirichlet过程混合模型 对于多模分布特性的数据,若使用所有的样本来训练一个分类器,则会增加分类器的训练复杂度,且容易忽视样本的内在结构.为此,文中引入混合专家模型,将数据集划分为若干子集,然后在各个子集上分别训练简单的分类器来构建全局非线性分类器.这样可以避免设计复杂分类器,大大简化分类器的设计难度.笔者在隐空间对数据进行聚类(划分子集),同时在每个聚类上学习一个LVSVM分类器.如此可以将聚类与后端的分类任务相结合,在一定程度上使得各个聚类上的样本局部可分,从而提高了全局的可分性. 不同于传统的聚类方法(如K-means),文中采用DP混合模型对数据隐变量进行聚类,避免了需要预先设定聚类个数的模型选择问题.Dirichlet过程是一种应用于非参数贝叶斯中的随机过程,它是一种基于分布的分布[14].若G服从DP,则记为G~DP(G0,α),其中G0为基分布,α为聚集参数.在DP混合模型中,G作为sn分布参数Θn的先验分布.基于Stick-breaking[15]构造的DP混合模型有如下结构: 可以看到,在DP混合模型中,整个参数空间被划分为无限可数(通常用较大值C进行截断)个离散点集合,共享同一个分布参数Θc的样本具有相同的分布,自动地划归为一个聚类.若假设每个聚类的样本服从高斯分布,则设定Θ={μ,Σ},其中μ表示均值,Σ表示协方差矩阵,此时基分布G0采用Normal-Wishart分布[4]. 进一步地,为了保证各个聚类的可分性,在每个聚类中学习一个以为输入的LVSVM分类器,从而构建了一种最大间隔DP混合模型.根据式(3)和式(4)可以推导出其参数的联合伪后验分布为 3.1无限最大间隔因子分析模型 笔者将BPFA模型和最大间隔DP混合模型相结合,提出了无限最大间隔Beta过程因子分析模型(IMMBPFA),来处理多模分布数据的分类问题.IMMBPFA模型具有以下优势:①采用BPFA模型来挖掘数据的隐含结构,相比于基于原始空间的算法灵活性更高,且降低了有效特征维度,减少了冗余信息;②两次利用非参数贝叶斯方法解决模型选择问题,即利用BP先验解决FA模型因子个数选择问题,以及利用DP混合模型解决子集划分问题;③采用LVSVM作为分类器,并将分类器的学习与数据描述、子集划分联合在一起,期望在特征空间得到可分性较好的数据聚类,从而提高全局的分类性能.由式(1)和式(5)可以得到IMMBPFA模型参数的联合伪后验分布为 3.2基于IMMBPFA模型的识别系统 如图1所示,笔者构建了一个基于IMMBPFA的识别系统.整个系统包括两部分:实线框内的训练阶段,即模型学习阶段和虚线框内的测试阶段.下面对这两个阶段进行介绍. 图1 基于IMMBPFA模型的目标识别系统框图 训练阶段,主要是对模型进行参数估计.如式(6)所示,由于采用LVSVM作为分类器,IMMBPFA模型整个层次化结构是完全共轭的,因而可以利用Gibbs采样技术对参数进行估计.在Gibbs采样的每次迭代中,所有参数均是从其条件后验分布的采样中获取的.由式(6)可以推导出所有参数的后验分布.其中, (1)隐变量sn的条件后验分布为 (2)因子选择变量znk的条件后验分布为 (3)样本聚类标记on的条件后验分布为 其中,{μc,Σc}表示第c个聚类中样本的分布参数. (4)第c个聚类的分类平面ωc的条件后验分布为 (5)隐变量λn的条件后验分布为 其中,IG(·)表示逆高斯分布. 从式(7)~式(9)中3个变量的条件后验分布形式可以看出,LVSVM可以将监督信息传递到数据描述(特征提取和特征选择)模型,从而使得整个模型更加适用于分类任务.其他参数的条件后验分布可根据文献[5,12-15]比较容易得出.根据Gibbs采样技术,由参数的条件后验分布可以构建一个马尔科夫链,在给定所有参数的初始值后,对参数的条件后验分布进行循环采样,从而得到IMMBPFA模型的所有参数的估计值.在预热阶段结束后,继续对参数进行循环采样,并从中抽取T0次采样进行存储. 分别在Benchmark数据集以及实测雷达高分辨距离像(High Resolution Range Profile,HRRP)数据上进行实验,来验证IMMBPFA模型的有效性.实验中将文中模型与5种模型进行了比较:单个线性SVM (SVM)与ILSVM两种线性模型以及K-means+线性SVM(K m+SVM)、DPMNL模型[11]和DPLVSVM模型[12]3种混合专家模型. 4.1Benchmark数据集 实验采用的数据集为从UCI Machine Learning Repository中获取的Benchmark数据集,并从中选取了Heart、Splice、Image、Twonorm这4个分布较复杂的数据.实验中采用原始数据作为模型输入,共重复10次,每次实验中随机地划分训练样本集和测试样本集且样本个数比例为7∶3.表1给出了数据的信息以及6种不同方法的分类结果. 表1 6种方法的分类结果对比 混合专家模型在每个数据子集上学习一个线性SVM分类器,构建了一个全局非线性的分类器,因而其分类性能总体上优于单个线性SVM分类器.由于ILSVM为线性模型而且其隐变量为二值变量,这使得其性能大部分情况下较差.然而由于ILSVM利用分类器和隐变量模型联合学习隐空间特征来保证隐空间特征的可分性,这使得其在Heart和Twonorm两个数据上有了较好的表现.DPMNL、DPLVSVM与IMMBPFA模型由于在划分子集的同时优化了分类器,使得每个子集具有很好的可分性,其分类性能优于子集划分与分类器学习相互独立的K m+SVM模型.DPMNL、DPLVSVM在原始空间对数据进行聚类和分类器学习,不仅受到冗余信息的影响,而且缺乏灵活性.相比之下,IMMBPFA模型利用BPFA模型对数据进行了特征提取和选择,在监督信息的指导下通过BP先验获得有利于分类的特征子集,因而更加灵活,而且降低了冗余信息对分类性能的影响.表1中IMMBPFA一栏括号中的数值为模型在各个数据中样本所选因子个数(有效特征的维数)的平均值.可以看出,IMMBPFA所提的特征维度小于数据原始维度,减少了冗余信息.由于特征提取、聚类和分类器学习同时进行,BPFA所提的特征较原始特征更具有可分性.从表中可以看到IMMBPFA模型在各个数据集上均取得了最好的分类结果. 4.2HRRP数据集 基于雷达高分辨距离像(HRRP)的目标识别是雷达自动目标识别领域研究的热点[2-3,11].本节实验对象为C波段雷达对三类飞机目标的实测HRRP数据.数据具体介绍见文献[2-3,11].实验中采用模2范数归一的方法消除HRRP的幅度敏感性,并提取功率谱特征消除其平移敏感性.为了检验模型的推广性能,文中采用与文献[2-3,11]相同的训练样本集与测试样本集,并从中选择600个训练样本和2 400个测试样本. 实验中设定K=50,即BPFA模型的因子个数设定为50.每个样本由模型自动选择相应的因子子集来对自身进行表达.图2给出了训练集和测试集样本选择的因子个数的分布情况.由于训练阶段为有监督的,而测试阶段为无监督的,因此,训练集和测试集样本选择的因子个数分布有所差异.然而,这两个分布基本上是相似的,其中大部分样本选择的因子个数均在30~37之间.从而证明了IMMBPFA模型在训练阶段和测试阶段的一致性(训练过程没有过匹配). 图2 训练集样本及测试集样本所选择因子个数的分布 HRRP数据维度较高,其中包含了大量与识别无益的冗余信息,可以通过降维方法减少冗余信息.表1中给出了不同方法对HRRP的识别结果.与SVM和K m+SVM相比,DPMNL和DPLVSVM的识别结果虽然有所提高,然而,由于受到冗余信息的影响,其识别性能仍受到限制.IMMBPFA则采用BPFA发掘HRRP数据的低维隐空间信息,利用BP先验进一步选择对分类有益的特征子集.实验中,HRRP样本平均选择的因子个数为33.2.可见,最终用于识别的有效特征的维数远小于其原始数据的维数,这大大降低了冗余信息对最终识别效果的影响,因而IMMBPFA模型获得了最高的识别率. 针对目标识别中具有多模分布特性的复杂数据,文中提出了一种IMMBPFA模型.该模型利用BPFA提取数据低维隐空间特征,并在该特征空间采用混合专家模型进行分类.不同于传统方法,IMMBPFA模型将数据降维(特征提取)、聚类以及分类器学习统一在概率框架下联合学习,不仅可以充分挖掘数据内在的分布结构,而且保证了各个聚类中样本的可分性.通过在公共数据集以及雷达实测数据上的实验,表明了IMMBPFA模型具有良好的分类性能. [2]DU L,LIU H W,BO Z.Radar HRRP Statistical Recognition:Parametric Model and Model Selection[J].IEEE Transactions on Signal Processing,2008,56(5):1931-1943.[3]DU L,LIU H W,WANG P H,et al.Noise Robust Radar HRRP Target Recognition Based on Multitask Factor Analysis with Small Training Data Size[J].IEEE Transactions on Signal Processing,2012,60(7):3546-3559. [4]BISHOP C.Pattern Recognition and Machine Learning[M].New York:Springer Science+Business Media,2007. [5]POLSON N G,SCOTT S L.Data Augmentation for Support Vector Machines[J].Bayesian Analysis,2011,6(1): 1-24. [6]ZHU J,AHMED A,XING E P.Med LDA:Maximum Margin Supervised Topic Model[J].The Journal of Machine Learning Research,2012,13(1):2237-2278. [7]ZHU J,CHEN N,PERKINS H,et al.Gibbs Max-margin Topic Models with Data Augmentation[J].The Journal of Machine Learning Research,2014,15(1):1073-1110. [8]BLEI D M,JORDAN M I.Variational Inference for Dirichlet Process Mixtures[J].Bayesian Analysis,2006,1(1): 121-144. [9]ZHU J,CHEN N,XING E P.Bayesian Inference with Posterior Regularization and Applications to Infinite Latent SVMs[J].The Journal of Machine Learning Research,2014,15(1):1799-1847. [10]ZHU J,CHEN N,XING E P.Infinite SVM:a Dirichlet Process Mixture of Large-margin Kernel Machines[C]// Proceedings of the 28th International Conference on Machine Learning.New York:ACM,2011:617-624. [11]SHAHBABA B,NEAL R.Nonlinear Models Using Dirichlet Process Mixtures[J].The Journal of Machine Learning Research,2009,10(4):1829-1850. [12]张学峰,陈渤,王鹏辉,等.一种基于Dirichlet过程隐变量支撑向量机模型的目标识别方法[J].电子与信息学报,2015,37(1):29-36. ZHANG Xuefeng,CHEN Bo,WANG Penghui,et al.A Target Recognition Method Based on Dirichlet Process Latent Variable Support Vector Machine Model[J].Journal of Electronics&Information Technology,2015,37(1):29-36 [13]PAISLEY J,CARIN L.Nonparametric Factor Analysis with Beta Process Priors[C]//Proceedings of the 26th International Conference on Machine Learning.New York:ACM,2009:777-784. [14]FERGUSON T S.A Bayesian Analysis of Some Nonparametric Problems[J].The Annals of Statistics,1973,1(2): 209-230. [15]SETHURAMAN J.A Constructive Definition of Dirichlet Priors[J].Statistica Sinica,1994,4(2):639-650. (编辑:李恩科) Infinite max-margin Beta process factor analysis model ZHANG Xuefeng,CHEN Bo,WANG Penghui,WEN Wei,LIU Hongwei An infinite max-margin Beta process factor analysis(IMMBPFA)model is developed to deal with the classification problem on multimodal data.In this model,BPFA is utilized to capture the latent feature of data.With the idea of mixture experts,IMMBPFA divides the data into‘infinite”clusters via the Dirichlet process(DP)mixture model in the low-dimensional latent space and meanwhile learns a linear max-margin classifier on each cluster to construct a complex nonlinear classifier.Since the proposed model jointly learns BPFA,clustering and max-margin classifier in a unified Bayesian framework,it exhibits superior performance in both data description and discrimination.With the help of nonparametric Bayesian inference and the Gibbs sampler,we avoid the model selection problem and can estimate the parameters simply and effectively.Based on the experimental data obtained from Benchmark and measured radar high resolution range profile(HRRP)dataset,the effectiveness of proposed method is validated. Beta process factor analysis(BPFA);mixture-of-experts;Dirichlet process mixture(DPM) model;max-margin classifiers TN959.1+7 A 1001-2400(2016)03-0013-06 10.3969/j.issn.1001-2400.2016.03.003 2015-02-10 时间:2015-07-27 国家自然科学基金资助项目(61372132,61201292);国家青年千人计划资助项目;新世纪优秀人才支持计划资助项目(NCET-13-0945);航空科学基金资助项目(20142081009);中央高校基本科研业务费专项资金资助项目(K5051302010) 张学峰(1987-),男,西安电子科技大学博士研究生,E-mail:zxf0913@163.com. http://www.cnki.net/kcms/detail/61.1076.TN.20150727.1952.003.html
2 最大间隔Dirichlet过程混合模型


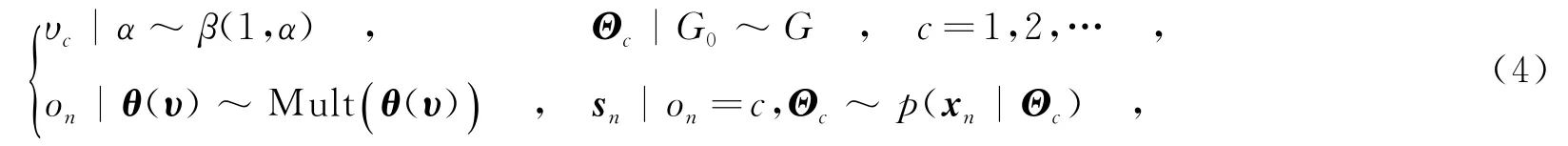

3 无限最大间隔因子分析模型
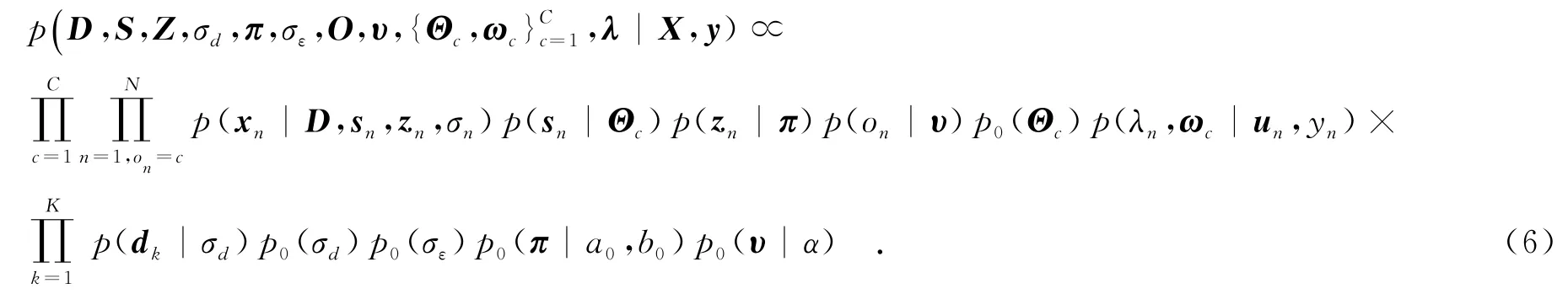





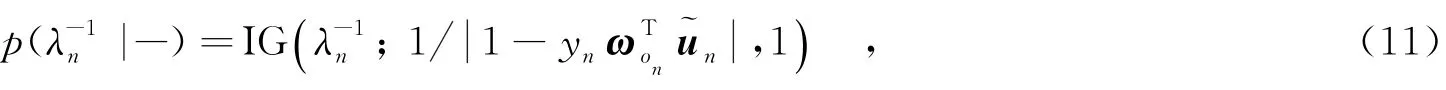
4 仿真实验


5 结 论
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)
