弹载双基前视SAR扩展场景成像算法设计

孟自强,李亚超,邢孟道,保 铮

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

弹载双基前视SAR扩展场景成像算法设计

孟自强,李亚超,邢孟道,保 铮

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

针对一种新型双基合成孔径雷达成像模式——弹载双基前视合成孔径雷达,由于收发平台较高速度和加速度的引入,距离历程存在双根号下高阶项问题和该构型相对单/双基直线轨迹合成孔径雷达更为严重的距离徙动问题,提出了一种消除位置空变性的扩展场景成像算法.首先在时域对距离走动量进行校正以减少二维耦合量;然后,基于级数反演求得的高精度二维频谱,对各相位项的场景空变性进行量性分析,并通过高阶多项式拟合设计出空变的匹配滤波器,完成扩大场景成像.该方法处理简洁且具有更少的运算量,利于弹载平台下成像分析和后续处理.仿真实验表明,该算法有效地校正了场景空变性,提高了场景边缘点的聚焦性能,从而扩大了成像场景范围.

弹载合成孔径雷达;成像算法;双基前视;空变性校正;级数反演

双基前视合成孔径雷达(Synthetic Aperture Radar,SAR)因其收发平台分置、几何配置灵活等优点,可实现正前方目标的二维较高分辨率成像,有效弥补了单基SAR无法对正前方目标二维成像的缺陷,而逐渐成为研究的热点[1-3].

弹载双基前视合成孔径雷达(Missile-borne Bistatic Forward-Looking Synthetic Aperture Radar,MBFL-SAR)是将双基前视SAR成像体制应用于弹载平台的双基地成像模式,在许多特定的场合下具有无可比拟的优势,尤其在导弹处于末端俯冲下降段,打击如舰母战斗群、近岸舰船编队等复杂背景目标时,船舶密集、岛岸林立、地形背景复杂,现有单脉冲雷达测角和单基SAR成像制导手段难以对目标区域进行全程二维高分辨成像探测,从而实现对目标的有效分离[4-5],而双基前视模式的低截获特点和隐身能力可使MBFLSAR实现弹载末端俯冲下降阶段全程二维成像、自主寻的精确制导,在地质探测、无人机协同作战、导弹主动寻的等方面具有潜在的体制优势.

与传统机载SAR相比,MBFL-SAR在下降过程中,收发平台均存在较大的速度和加速度,在距离历程中引入的双根号形式和高次项使其表现出更为严重的距离徙动问题,所以传统的驻定相位原理(Principle Of Stationary Phase,POSP)[6]不能直接得到其二维频谱.针对弹载SAR下降段成像,文献[7]针对大斜视成像,提出了基于高次相位滤波的方位空变校正方法,改善了方位聚焦深度;文献[8-9]结合“级数反演”的思想,获得信号的高精度二维频谱表达式,提出了俯冲加速弹载SAR成像算法.针对双基前视成像,文献[2]通过对距离历程双根号近似为单根号形式,提出了调频变标算法;文献[10]针对单站固定式双基前视SAR提出了方位非线性变标算法;文献[11]针对双基前视SAR聚束模式进行了研究并提出双基极坐标格式算法(Polar Format Algorithm,PFA).但这些文献均不是针对弹载双基平台的前视构型进行的研究,需要在这些研究成果的基础上专门分析MBFL-SAR距离历程以及回波信号的特点,以明确该构型下成像算法研究的必要性.

笔者针对MBFL-SAR这种特殊的双基前视成像模式,首先结合双基成像构型及弹载SAR运动特点,建立了MBFL-SAR的距离历程模型及回波模型;在此基础上,利用级数反演理论求得其回波信号的高精度二维频谱,并对该频谱对各相位项的空变性进行了详细量化分析;最后,通过高阶多项式拟合,设计高效的频域成像算法消除了目标位置的空变性,从而扩大了成像场景范围.

1　MBFL-SAR空间几何构型及回波模型

图1为MBFL-SAR俯冲下降段成像几何构型,O为直角坐标系原点,为表述方便,发、收平台的运动关系分别在坐标系x Oyz和x′Oy′z中表示.发射机在与平面y Oz成ψ夹角的平面内沿曲线进行下降运动,斜视持续照射成像区域(图中阴影部分),瞬时速度为vt,vt在y′方向和z方向的分量分别记为vty′与vtz;接收机在y Oz平面内沿曲线做下降运动,前视接收目标区域回波,其瞬时速度为vr,vr在y方向和z方向的分量分别记为vry与vrz. P(xp,yp,0)为测绘带内一个点目标.

图1　弹载双基前视SAR下降段几何构型

设慢时间tm=0时,HR和HT分别表示收、发机的高度,此时两平台在坐标系x Oyz和x′Oy′z中的位置分别为R0(0,0,HR)和T0(x′t,0,HT),O′为T0在水平面内的投影.(0,vry0,vrz0)和(0,vty′0,vtz0)为此时速度向量,(0,ary,arz)和(0,aty′,atz)为加速度向量.在任意tm时刻接收机在坐标系x Oyz中的位置坐标可表示为;发射机在坐标系x′Oy′z中的位置坐标可表示为(x′t,,则雷达与目标P(xp,yp,0)之间的瞬时双基斜距可表示为

其中,(x′p,y′p,0)为点目标(xp,yp,0)在发射机坐标系中的位置.

假设发射调频率为γ的线性调频信号,则目标P(xp,yp,0)的基频回波信号可以表示为

其中,wr)、wa(tm)分别为雷达线性调频信号的窗函数和方位窗函数,为快时间,tm为慢时间,c为光速,λ为波长.可以看出,MBFL-SAR点目标的回波信号模型与传统模式的回波模型相同.

2　MBFL-SAR二维频谱推导及相位空变性分析

2.1MBFL-SAR二维频谱推导

由于收发平台较高速度和加速度的引入,且运动方向不同,MBFL-SAR存在严重的距离走动量.这里首先在方位时域校正距离走动量以减少二维耦合量;同时针对距离历程中引入的高次项,在对距离历程高阶近似的基础上采用级数反演理论,求得其回波信号的高精度二维频谱.

其中,fr表示距离频率.为减小距离/方位的耦合量,在距离频域-方位时域进行线性走动量校正,校正因子可表示为

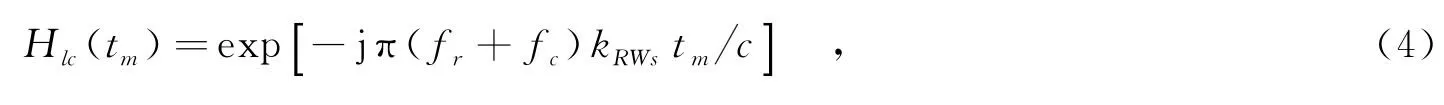
其中,kRWs为场景中心对应距离走动量系数.

将式(3)所示的信号s(fr,tm)与式(4)相乘,得到信号形式,即

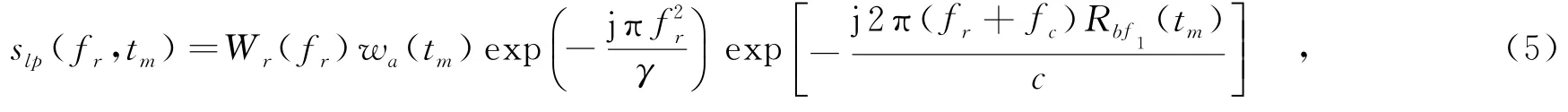
其中,Rbf1(tm)=Rbf(tm)-kRWstm,表示线性走动量校正后的斜距.

根据文献[12],基于距离的高阶项近似可有效获得信号的高精度二维频谱,因此这里通过级数反演理论,利用多普勒频率的展开式反演出驻相点展开式的系数.根据SAR性质可知[6],斜距近似式引入的相位误差远小于π/4时可忽略其对成像的影响.由于弹体在运动过程中速度较大且存在加速度,高度不断下降,双基斜距在短时间内变化剧烈,需要采用三阶近似方能满足成像要求,即

利用级数反演理论,可求得回波信号的高精度二维频谱表示为

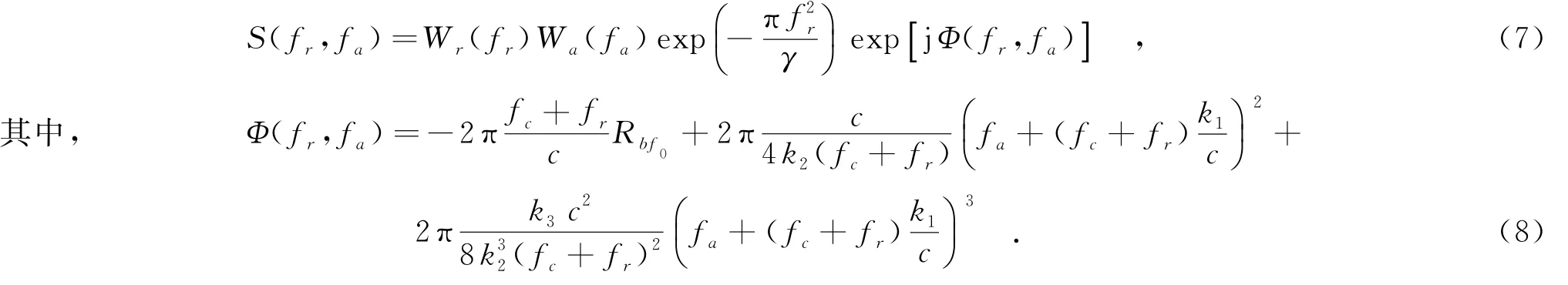
2.2频谱相位空变性分析及校正

由式(8)可知,回波信号的二维频谱存在fr和fa的耦合,不利于后续成像处理.因此将式(8)在fr=0处进行泰勒级数展开(这里保留到三次项),整理得到如下形式:

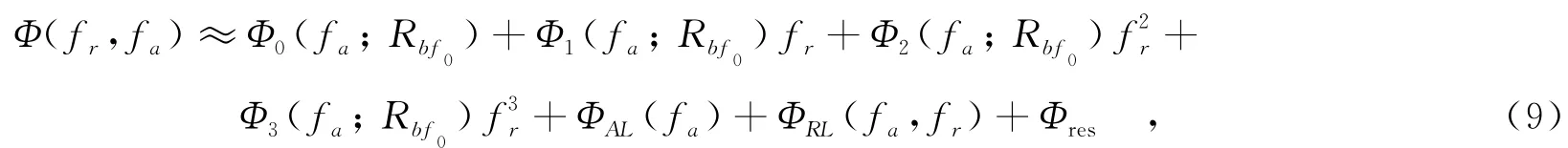
其中,Φ0(fa;Rbf0)为方位压缩项,该项如果不能精确补偿,会导致图像的方位散焦;表示距离徙动项,为二次距离脉冲压缩(SRC)项,为三次项,这3项表示距离向与方位向的耦合,其补偿精度直接影响到成像聚焦性能;ΦAL(fa)和ΦRL(fr)分别表示目标点聚焦的方位和距离位置,Φres为残余项,这3项不影响成像的聚焦性能,可不予考虑,这里重点针对式(9)右端前4项进行分析.式(9)中表达式具体为

由于MBFL-SAR收发平台的较高速度和加速度的存在,以上各相位项均具有随Rbf0的空变性,下面对其进行具体分析.由于在二维频域内同时无法对fr,fa和Rbf0这3个变量进行分析,因此,这里采用文献[13]中近似写为以Rbf0为变量的表达式,即

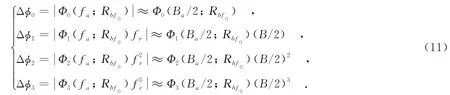
其中,Ba为多普勒带宽,B为发射信号带宽.

按照表1参数,可计算得到频谱各相位项对Rbf0的变化曲线,结果如图2所示.

表1　MBFL-SAR仿真实验参数

根据运动参数和仿真结果,可看出,Δϕ0的变化范围约为261.72 rad,远大于相位误差门限(π/4)rad,空变性严重;Δϕ1的变化范围约为0.93 rad,略大于(π/4)rad.而其他两个相位项的变化则很小,Δϕ2的变化范围约为3.28×10-3rad,Δϕ3的变化范围约为1.16×10-5rad,这两项的空变可忽略.对于空变严重的Δϕ0和Δϕ1,如果忽略这两项空变,统一采用场景中心设计匹配滤波器,成像场景范围则会受到很大限制,必须设计空变的滤波器以尽可能减小该空变对成像的影响,而相位的空变性是由斜距Rbf1(tm)泰勒展开系数k1、k2、k3随Rbf0的空变所致,因此,这里通过高阶多项式拟合消除该空变,即

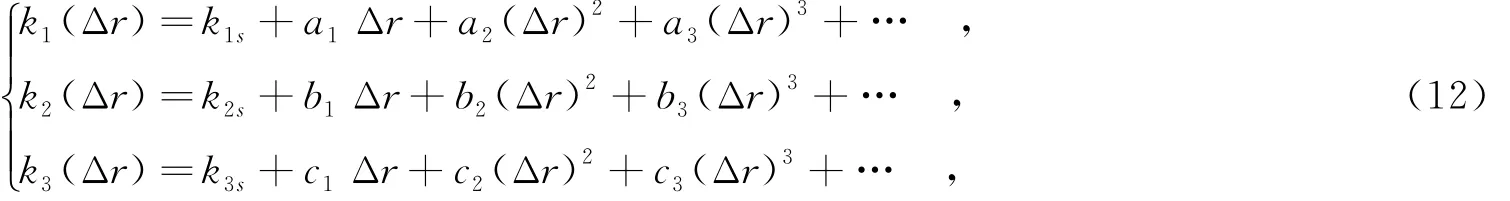
其中,k1s、k2s、k3s分别为场景中心点对应系数,ai、bi、ci(i=1,…,N;N为拟合阶数)为拟合系数,Δr为场景中其他目标点相对中心点的斜距差异.

利用高阶多项式拟合得到以上与场景相关的泰勒系数,即可设计空变的匹配滤波器,减小场景位置引起的空变,空变校正前后的相位误差如图3所示,由结果可知,经过空变性校正之后,相位误差大为减小,为后续精确成像提供理论基础.

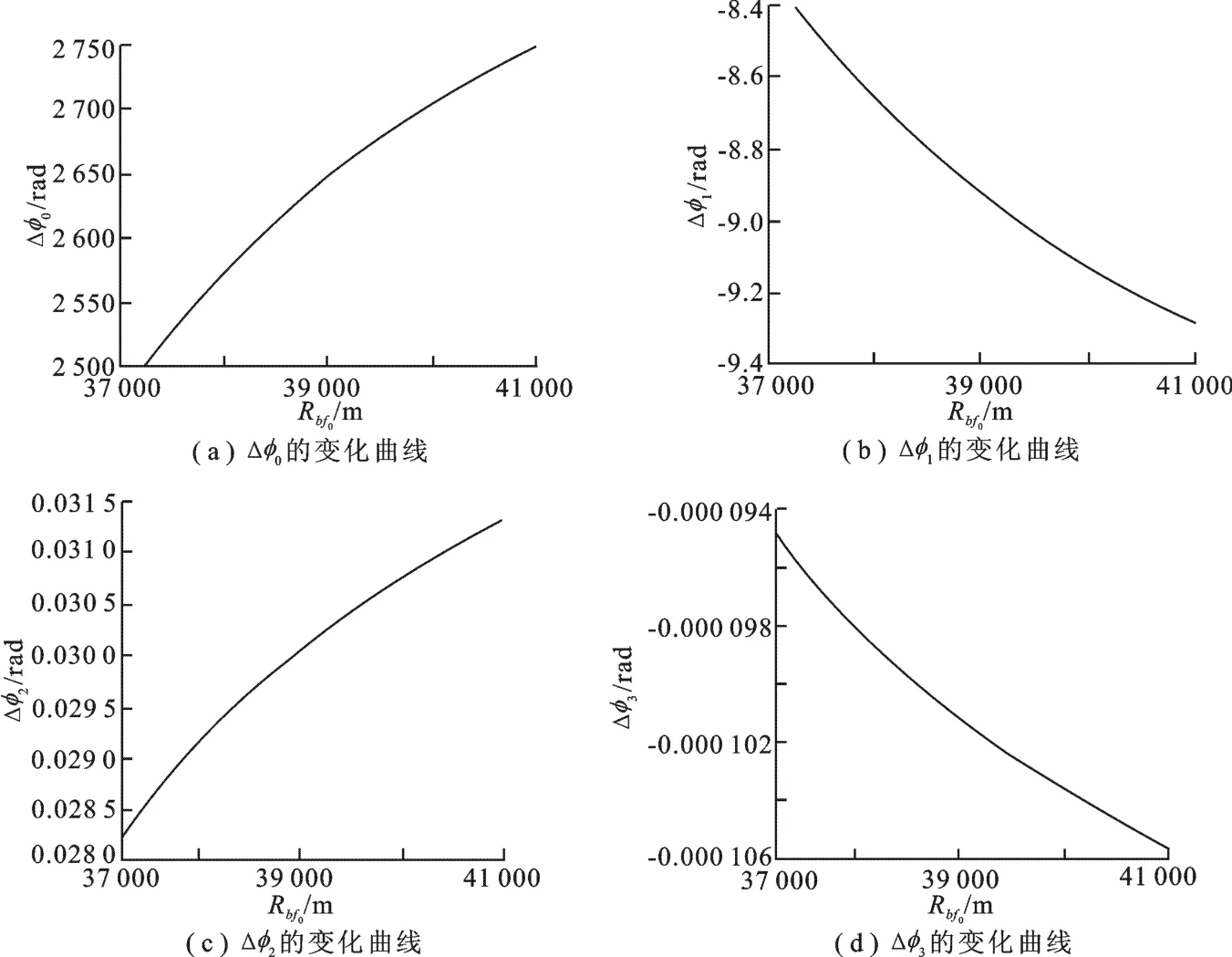
图2　频谱各相位项随Rbf0的变化曲线

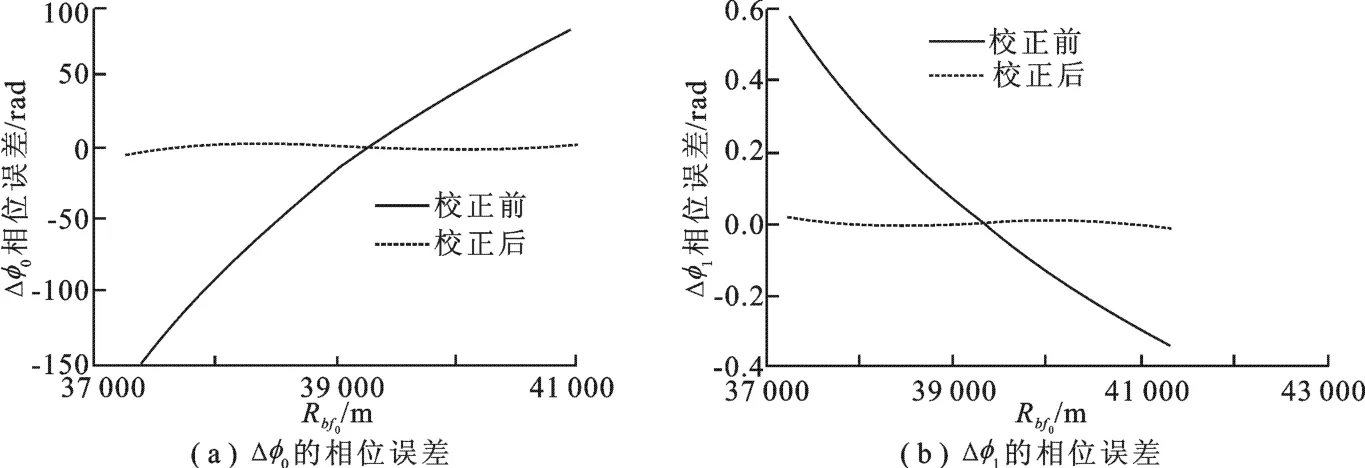
图3　空变校正前后的相位误差

3　MBFL-SAR成像算法设计及分析

3.1成像处理

基于以上场景空变性校正,在得到二维频谱后,可在二维频率域设计随距离空变的匹配滤波器Hrc(fr,fa)和Hrcm(fr,fa),完成距离脉冲压缩和空变的距离徙动校正;距离快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)后在距离-多普勒域设计匹配滤波器Ha(fa)以完成方位脉冲压缩,得到聚焦后的SAR图像.其中,空变匹配滤波器为

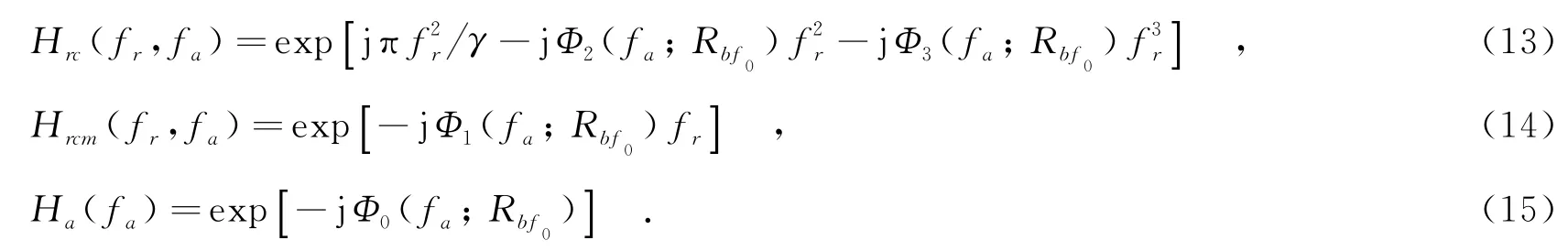
在具体实现过程中,为便于后续匹配滤波器设计和成像的处理,可在斜距等效处理后完成对场景空变性校正,然后在二维频域实现距离压缩和徙动校正,最后在距离-多普勒域完成方位脉冲压缩.其算法流程如图4所示.

3.2运算量分析

快速高效的运算在高速平台下尤为重要,根据图4,算法中的所有操作均由快速傅里叶变换(Fast Fourier Transform,FFT)和相位点乘完成,具有较高的运算效率,这里计算文中算法所需的浮点运算量(FLOP),借助文献[6]中FFT和复数相乘的计算方法,假设距离向和方位向的采样点数分别为Nr和Na,则算法所需总运算量为

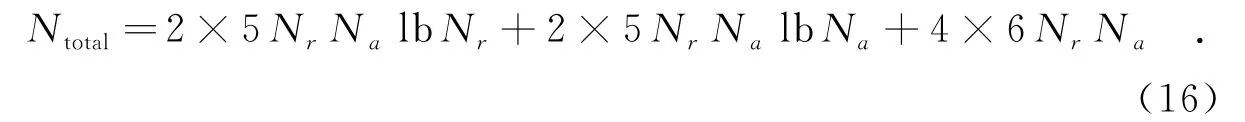
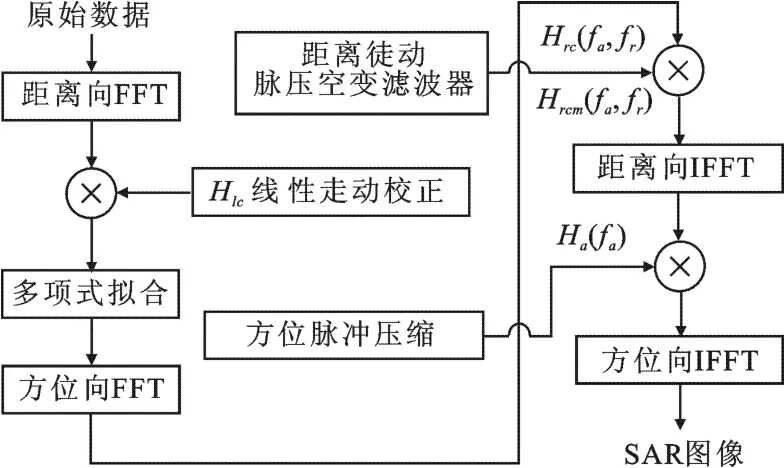
图4　算法流程图

如果距离向和方位向的采样点数相等,即Nr=Na,可求得算法运算复杂度为O(N2lb N),相对于时域算法后向投影(Back Projection,BP)算法的复杂度O(N3)而言已有很大提高.根据文献[6],当Nr=Na=2 048时,文中算法运算量为1.02×109次FLOP,而对于常用的单基SAR成像插值类算法中,精确距离-多普勒算法处理相同数据则需要5.6×109次FLOP,精确Omega-K算法也需要4.4×109次FLOP,可见文中算法具有更少的运算量,适用于弹载高速平台下的成像与分析.

4　仿真成像结果与分析

为验证分析的正确性和算法的有效性,本节通过计算机仿真成像.参数如表1所示,场景中心A位于(0,8 500,0),目标场景采用9个点目标构成的点阵,仿真尺寸为1 000 m×500 m.

图5给出了目标点阵聚焦结果,图5(a)表示场景空变性校正前的成像结果,可以明显看出,由于采用场景中心处统一设计的匹配滤波器,两个边缘点在方位向散焦严重;为充分验证文中算法在MBFL-SAR构型下的有效性,利用文献[2]中的方法进行仿真,结果如图5(b)所示,由于该方法在MBFL-SAR构型下对距离历程的近似误差较大,边缘点仍存在散焦;图5(c)为采用文中方法得到的结果,可看出边缘点聚焦性能得到了很大提高.另外,表2进一步给出了场景目标A、B和C的成像质量参数,利用峰值旁瓣比(Peak Side-Lobe Ratio,PSLR)和积分旁瓣比(Integrated Side-Lobe Ratio,ISLR)对成像质量进行评估,由于弹体较大速度和加速度的存在,场景远点相对场景中心点聚焦性能略微下降,但与理论值相差不大,良好的聚焦效果进一步验证了文中算法的正确性和可行性.

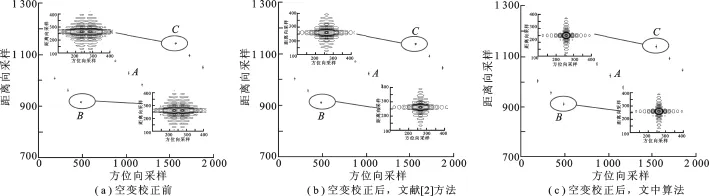
图5　场景成像结果

表2　文中算法的成像质量参数

5　结束语

作为一种将双基前视成像体制应用于弹载平台的新型SAR模式,MBFL-SAR可实现末端俯冲下降阶段全程二维成像、自主寻的精确制导.笔者根据其运动几何关系,建立其距离历程及回波信号模型,利用级数反演的思想得到了具有较高精度的二维频谱,并在之后的成像处理中,通过高次精确拟合运动参量消除了场景位置的空变性,扩大了场景成像范围.该算法相对于其他算法不但运算高效且聚焦性能良好,为该新型SAR成像模式的算法研究获取了一种有效的思路.

[1]LI Y C,MENG Z Q,XING M D,et al.Configuration Study of Missile-borne Bistatic Forward-looking SAR[C]// Proceedings of IEEE China Summit&International Conference on Signal and Information Processing.Piscataway: IEEE,2014:184-188.

[2]QI C D,SHI X M,BIAN M M,et al.Focusing Forward-looking Bistatic SAR Data with Chirp Scaling[J].Electronics Letters,2014,50(3):206-207.

[3]VU V T,PETTERSSON M I.On Bistatic Forward-looking SAR Imaging[C]//Proceedings of IEEE International Geoscience and Remote Sensing Symposium.Piscataway:IEEE,2014:3953-3956.

[4]毕开波,杨兴宝,陆永红.导弹武器及其制导技术[M].北京:国防工业出版社,2013.

[5]杨立波,任笑真,杨汝良.末制导合成孔径雷达信号分析及成像处理[J].系统工程与电子技术,2010,32(6): 1176-1181. YANG Libo,REN Xiaozhen,YANG Ruliang.Signal Analysis and Imaging Processing of Terminal Guidance Synthetic Aperture Radar[J].Systems Engineering and Electronics,2010,32(6):1176-1181.

[6]CUMMING I G,WONG F H.Digital Processing of Synthetic Aperture Radar Data:Algorithms and Implementation [M].Norwood:Artech House,2005.

[7]李震宇,杨军,梁毅,等.弹载SAR子孔径大斜视成像方位空变校正新方法[J].西安电子科技大学学报,2015,42 (4):99-105. LI Zhenyu,YANG Jun,LIANG Yi,et al.New Method for Azimuth-dependent Correction of the Highly Squint Missileborne SAR Subaperture Imaging[J].Journal of Xidian University,2015,42(4):99-105.

[8]刘高高,张林让,易予生,等.一种曲线轨迹下的弹载前斜视成像算法[J].西安电子科技大学学报,2011,38(1): 123-130. LIU Ggaogao,ZHANG Linrang,YI Yusheng,et al.Missile-borne Squint SAR Algorithm Based on a Curve Locus[J]. Journal of Xidian University,2011,38(1):123-130.

[9]易予生,张林让,刘楠,等.基于级数反演的俯冲加速运动状态弹载SAR成像算法[J].系统工程与电子技术,2009,31(12):2863-2866. YI Yusheng,ZHANG Linrang,LIU Nan,et al.Imaging Algorithm for Missile-borne SAR with Diving Acceleration Based on Series Reversion[J].Systems Engineering and Electronics,2009,31(12):2863-2866.

[10]WU J J,LI Z Y,HUANG Y L,et al.Focusing Bistatic Forward-looking SAR with Stationary Transmitter Based on Keystone Transform and Nonlinear Chirp Scaling[J].IEEE Geoscience and Remote Sensing Letters,2014,11(1): 148-152.

[11]ZHANG H R,WANG Y,LI J W.New Applications of Parameter-adjusting Polar Format Algorithm in Spotlight Forward-looking Bistatic SAR Processing[C]//Proceedings of Asia-Pacific Conference on Synthetic Aperture Radar. Washington:IEEE Computer Society,2013:384-387.

[12]NEO Y L,WONG F,CUMMING I G.A Two-dimensional Spectrum for Bisstatic SAR Processing Using Series Reversion[J].IEEE Geoscience and Remote Sensing Letters,2007,4(1):93-96.

[13]周鹏,周松,熊涛,等.基于级数反演的弹载SAR下降段CZT成像算法[J].电子与信息学报,2010,32(12): 2861-2867. ZHOU Peng,ZHOU Song,XIONG Tao,et al.A Chirp-Z Transform Imaging Algorithm for Missile-borne SAR with Diving Maneuver Based on the Method of Series Reversion[J].Journal of Electronics&Information Technology,2010,32(12):2861-2867.

(编辑:王 瑞)

Imaging method for the extended scene of missile-borne bistatic forward-looking SAR

MENG Ziqiang,LI Yachao,XING Mengdao,BAO Zheng
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)

Due to such problems as high order terms in double square roots and more serious range cell migration than monostatic or bistatic SAR in range history,caused by high velocities and accelerations in both the transmitter and the receiver platforms in a new and special bistatic synthetic aperture radar imaging mode,i.e.,missile-borne bistatic forward-looking synthetic aperture radar,an imaging algorithm correcting space variance for the extended scene for is proposed.The range walk is firstly corrected in the time domain to reduce the two dimensional(2D)coupling.And then the space variance of phase terms,in the 2D frequency spectrum of the echo signal with high precision gained by the method of series reversion,is analyzed quantitatively.The imaging is completed through polynomial fitting and variant match filter designing.With simple operation and less computation,our algorithm is convenient for imaging processing and subsequent procedure in the missile-borne platform.Simulation results show our imaging method significantly corrects the space variance,improves the focus quality of fringe targets,and thus extends the imaging scene.

missile-borne synthetic aperture radar;imaging algorithm;bistatic forward-looking;space variance revision;series reversion

TN957

A

1001-2400(2016)03-0031-07

10.3969/j.issn.1001-2400.2016.03.006

2015-03-05

时间:2015-07-27

国家自然科学基金资助项目(61001211,61303035,61471283);中央高校基本科研业务费专项资金资助项目(K5051202016)

孟自强(1988-),男,西安电子科技大学博士研究生,E-mail:mengziqiang@hotmail.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20150727.1952.006.html