桩−土−结构相互作用下新型抗拔摩擦摆支座对单层柱面网壳结构地震响应的影响

刘毅，薛素铎，潘克君，李雄彦

(1. 北京工业大学 建筑工程学院，北京，100124；2. 中车建设工程有限公司，北京，100078 3. 北京市弘都城市规划建筑设计院，北京，100045)

桩−土−结构相互作用下新型抗拔摩擦摆支座对单层柱面网壳结构地震响应的影响

刘毅1,2，薛素铎1，潘克君3，李雄彦1

(1. 北京工业大学 建筑工程学院，北京，100124；2. 中车建设工程有限公司，北京，100078 3. 北京市弘都城市规划建筑设计院，北京，100045)

基于设计提出的铜基面抗拔摩擦摆支座(FPB)试验研究和数值模拟，将铜基面抗拔摩擦摆支座以双线性模型简化，并结合桩−土−结构相互作用(PSSI)、黏弹性人工边界相关理论，采用整体有限元法建立桩−土−结构相互作用的隔震(PSSII) 单层柱面网壳结构模型，研究桩−土−结构相互作用下铜基面抗拔摩擦摆支座对网壳结构地震响应的影响及地震波输入的空间效应问题。研究结果表明：铜基面抗拔摩擦摆支座使桩−土−结构作用下的网壳结构的节点加速度峰值衰减50%～60%，网壳杆件的内力衰减50%～80%，地震波频谱特性对抗拔摩擦摆支座的隔震效应有着不可忽略的影响；PSSII体系网壳节点加速度最大值未必在地震波垂直入射时最大，入射角度45°～60°是一重要的考虑区间；当地震波入射角度为55°～80°时，在进行抗震计算时可按国家标准规定进行地震波输入，当不在此范围时，不宜按照规范规定进行地震波输入，应考虑地震波的空间效应。

单层柱面网壳结构；桩−土−结构相互作用；竖向抗拔摩擦摆支座；地震响应；入射角度

大跨空间结构具有自重轻、柔性大、阻尼小的特点，对地震荷载较敏感[1]，地震荷载是评价大跨空间结构安全性的重要指标。传统结构抗震设计方法主要依靠增加结构或构件自身的强度、延性、耗能能力来抗震，该方法容许很大的地震能量从地面传递给结构，可确保结构的整体性和防止结构倒塌的发生，但易导致结构构件的损伤。随着大跨空间结构广泛用于大型体育场馆、会展中心、机场机库、大型娱乐场所等公共建筑，其跨度越来越大，且结构形式不断创新，传统的抗震设计方法越来越难以满足结构的安全性和适用性要求。于是部分学者开始研究新抗震技术，主要包括被动控制技术、主动控制技术、半主动控制技术及混合控制技术[2]。被动控制技术具有无需外部能量供给、工作条件要求较低、工作性能稳定性易保证等优点，在实际工程中得到了广泛的研究和应用[3]。隔震技术是被动控制技术中的一种控制机理，通过在上部结构与下部支承结构或基础之间设隔震消能装置，减小地震能量向上部的传输，从而达到减小上部结构振动的目的，发展的较早且成熟，在工程中应用广泛。肖建春等[4]提出了预应力网壳结构中加劲板式橡胶支座的计算模型及设计方法，可充分利用预应力，有效地将网壳与支承结构连成整体。施卫星等[5]在上海国际赛车场新闻中心屋盖结构采用复合隔震支座实现高位隔震，通过利用滑动摩擦耗能及橡胶支座提供的侧移刚度限制支座发生过大的水平变形，降低了结构的地震反应。徐庆阳等[6]通过建立柱与网架屋盖相互作用的整体模型，研究了在柱顶设置铅芯橡胶支座和滑移支座隔震装置对网架结构地震响应的影响。陆伟东等[7]对昆明新国际机场航站楼进行了1/60缩尺的振动台试验，试验通过在基础部位设置铅芯橡胶支座，研究了在隔震工况下机场航站楼地震响应与不考虑隔震工况下响应的差异。朱忠义等[8]结合深圳机场T3航站楼屋顶，采用整体隔震模型，研究了普通叠层橡胶垫、铅芯橡胶垫对T3航站楼结构减震耗能作用。李雄彦等[9]基于网架大跨维修机库，开发了相应的复合摩擦隔震支座，并根据试验结果提出相应的计算理论模型。现阶段对于大跨隔震技术的研究集中于上部屋盖结构或屋盖结构与支承体系的整体结构，对同时考虑土−结构相互作用和隔震耦合条件下大跨空间结构动力性能的研究未见相关报道。因此，从建立土−结构相互作用和隔震相耦合模型出发，研究大跨空间结构的抗震性能具有重要意义。本文作者基于设计提出的铜基面抗拔摩擦摆支座、桩−土−结构相互作用、黏弹性人工边界等相关理论，结合试验和数值模拟结果将铜基面抗拔摩擦摆支座以双线性模型简化，并获得新型抗拔摩擦摆支座的摩擦因数。采用整体有限元法建立桩−土−结构相互作用的隔震(PSSII)单层柱面网壳结构模型，同时建立桩−土−结构相互作用(PSSI)单层柱面网壳结构模型，研究桩−土−结构相互作用下铜基面抗拔摩擦摆支座对网壳结构地震响应的影响，同时研究地震波输入的空间效应问题，分析在Northridge波和Kobe波作用下PSSII体系中网壳结构杆件内力、节点位移、加速度响应。

1　铜基面抗拔摩擦摆支座

1.1支座构造

铜基面抗拔摩擦摆支座由下底座、中间滑块、抗拔挡板、挡块、上部盖板等部分构成，如图1所示。滑槽内滑动面上附有自主研发的新型青铜基复合减摩材料，该材料具有摩擦因数小、承载力高的特点，滑块下表面为抛光不锈钢板，采用镀铬处理，以减小滑动面间的摩擦因数。滑块上球面和挡块下球面间的相对转动提供支座的转动能力，滑块在滑槽中的滑动产生水平位移，挡块和抗拔挡板之间的接触实现抗拔。

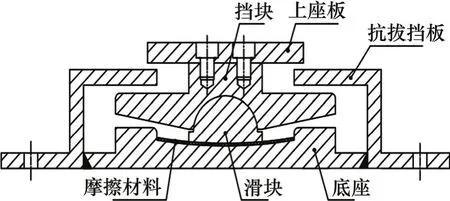
图1　支座示意图Fig. 1 Schematic diagram of bearing

1.2支座试验及有限元模拟

试验模型为FPB3000型竖向抗拔摩擦摆支座，支座竖向设计承载力为3 MN，抗拔承载力为600 kN，设计转角为0.06 rad，径向允许位移为70 mm，采用铸钢ZG275−485H及Q235制造，材料本构关系选用弹塑性模型，钢材的弹性模量为2.1×1011Pa，泊松比为0.3，设计强度为210 MPa，屈服强度为235 MPa，极限强度为425 MPa，摩擦材料为铜基复合材料。

试验主要测试FPB3000型竖向抗拔摩擦摆支座的滞回性能及摩擦因数，竖向加载为1，2和3 MN；水平向采用位移控制，采用正弦位移曲线，控制幅值(±Am)为±70 mm，加载频率分别为0.05 Hz与0.10 Hz；试验加载方案如表1所示，对FPB3000进行有限元模拟，与试验数据进行对比，三维数值有限元模型，如图2所示。

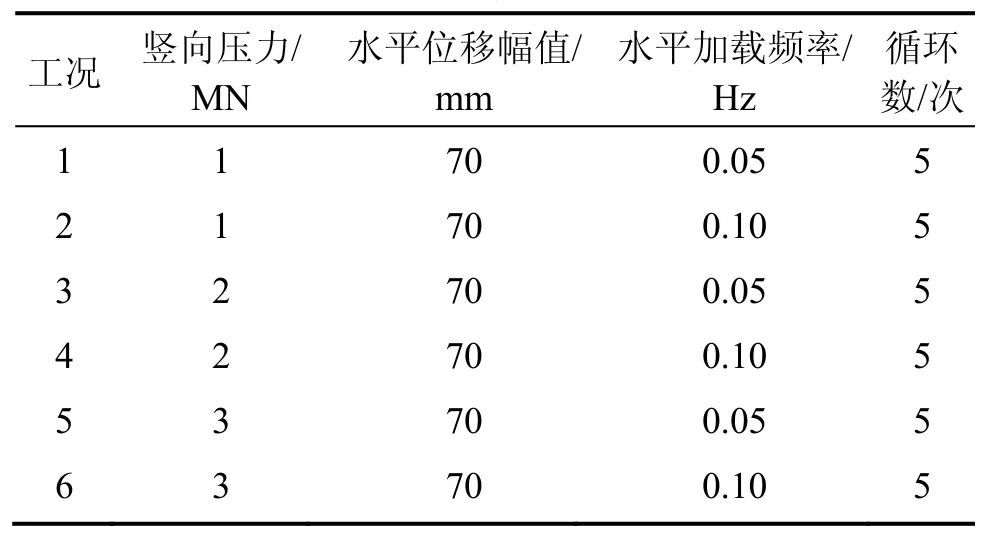
表1　滞回性能试验加载方案Table 1 Experimental loading scheme of hysteretic property

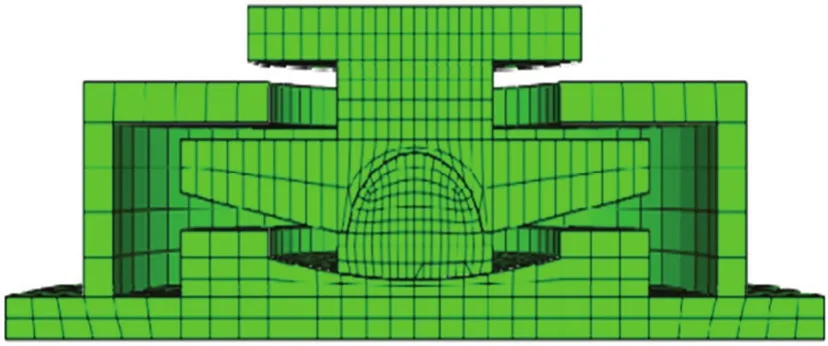
图2　有限元模型Fig. 2 Finite element model

图3所示为FPB3000水平力数值模拟和试验的滞回曲线对比图，表2所示为数值模拟与试验曲线在控制幅值为−Am/2，0和Am/2的水平力差值。由图3和表2可看出：试验所得水平力与数值模拟值吻合较好。考虑到试验设备系统误差、数据采集误差、加工误差等不确定因素的影响，可认为该支座的三维数值模拟是合理的且具有较好的精度。表3所示为不同工况下支座的摩擦因数，摩擦因数的平均范围为0.096～0.107。

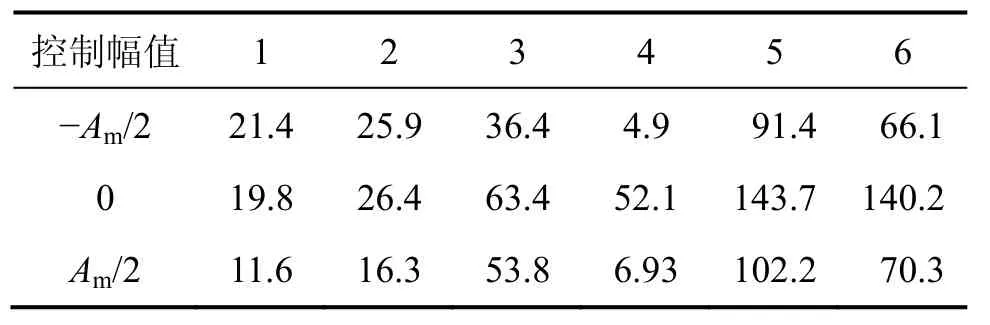
表2　水平力差值Table 2 Horizontal difference value　kN

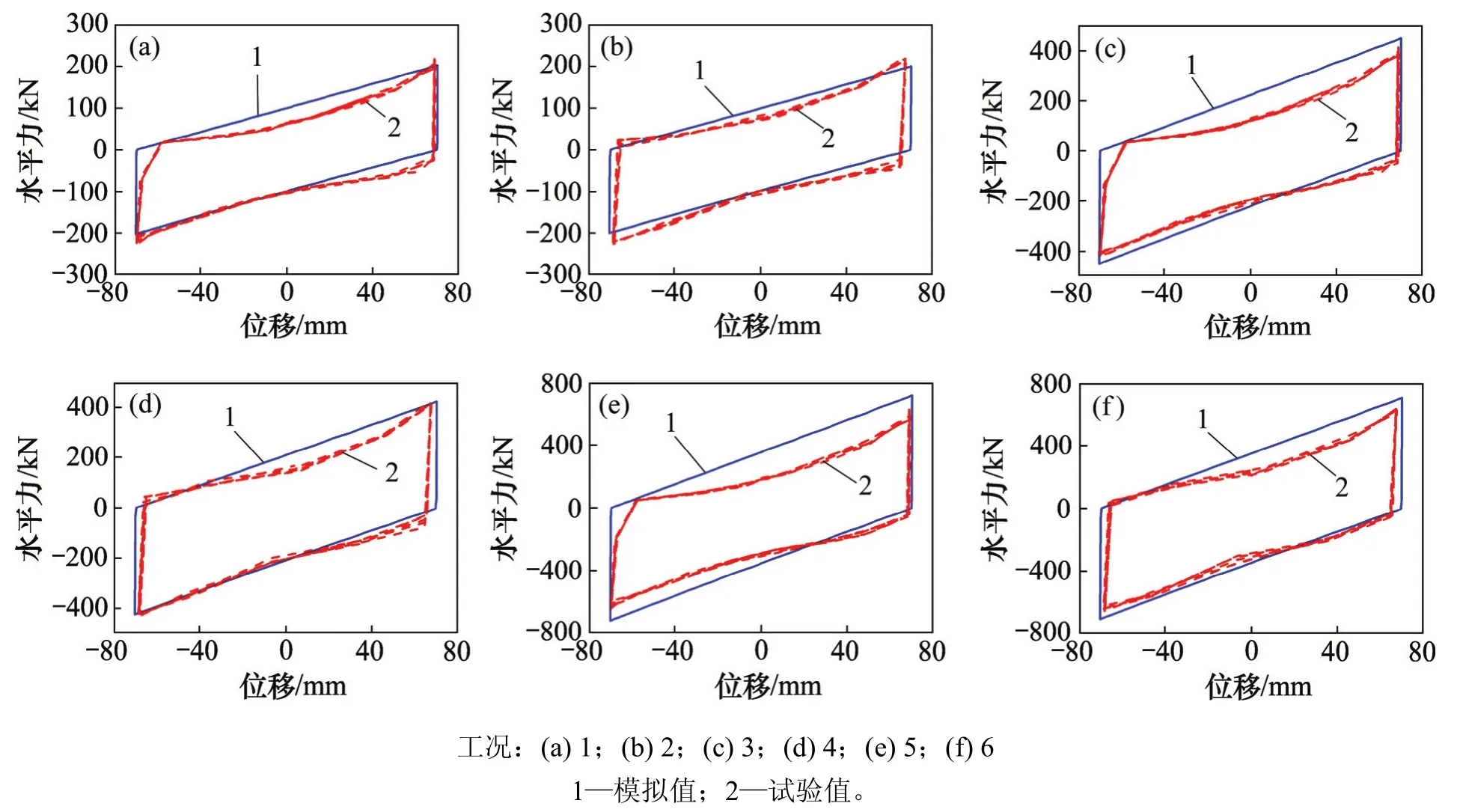
图3　模拟与试验滞回曲线对比Fig. 3 Hysteretic loops comparisons between simulation and experiment

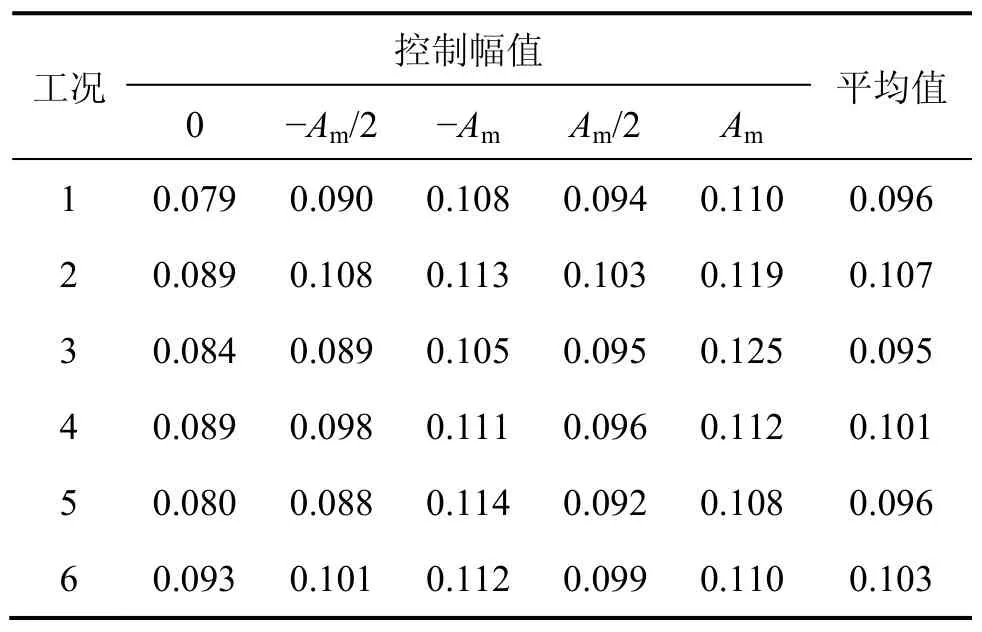
表3　不同工况下摩擦因数Table 3 Friction coefficient under various conditions

2　桩−土−结构相互作用

用有限元法对无限域或半无限域进行动力分析时，为精确反映结构与地基土的动力相互作用，通常的作法是人为截取一定的地基土域，并在土域的边界设置人工边界模拟近场能量向无限域的散射。在近场波动有限元分析中，人工边界面l结点i方向的集中质量有限元总波场运动方程[10]为

式中：ml为结点l的集中质量；klikj和clikj分别为结点k方向j对于结点l方向i的刚度和阻尼系数；ukj和分别为结点k方向j的位移和速度；为结点l方向i的加速度；fli为在结点l方向i处无限远场对有限近场的作用应力；Al为人工边界面上结点l的影响面积。对于三维问题，n=3，即下标i和j为1, 2, 3，分别对应直角坐标x, y, z。将人工边界处的总波场分解为内行场(上标R表示)和外行场(上标S表示)。内行场是指就人工边界的局部而言从无限域通过人工边界进入有限域的波场，而外行场是指从有限域通过人工边界进入无限域的波场。人工边界结点l方向i的总位移uli和作用应力fli可分别写为：

外行场采用黏弹性人工边界条件模拟，人工边界结点l方向i的应力−运动关系可以写为

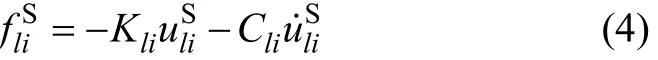
式中：uli为结点l方向i处位移；分别为内行场、外行场在结点l方向i处产生的位移；分别为内行场、外行场在结点l方向i处产生的作用应力；Kli和Cli分别为结点l方向i的弹簧刚度系数和阻尼系数，参照表4进行选取。表4中：E为地基的弹性模量；λ和G为拉梅常数；ν为土体的泊松比；ρ为地基的质量密度；R为结构的几何中心到人工边界的距离；A和B为量纲一的常数，依次推荐取为0.8和1.1； cp和cs为地基的纵波和横波波速。

表4　三维黏弹性边界弹簧刚度系数和阻尼系数Table 4 Spring stiffness and damping coefficient of three dimensional viscoelastic boundary

由式(1)～(4)整理可得

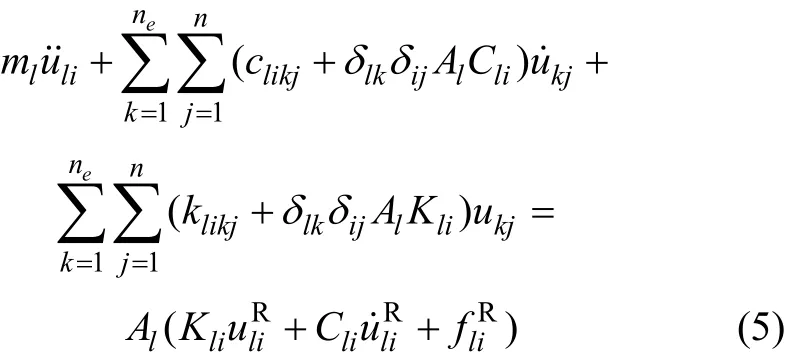
式中：δij=1(i =j时)；δij=0(i ≠j时)。

式(5)为考虑无限域辐射阻尼和地震波输入条件下人工边界结点的集中质量有限元运动方程。其中，式(5)左边增加的2项为模拟波场向无限域辐射而施加的黏弹性人工边界条件，其物理角度相当于在结点l方向i施加1个另一端固定的并联弹簧−阻尼器单元，如图4所示，其中KBT和CBT为切向弹簧刚度和阻尼系数，KBN和CBN为法向弹簧刚度和阻尼系数。

式(5)右边表示地震荷载，即通过入射波得到的人工边界结点l方向i处的内行场所对应的等效荷载，其中前2项表示产生内行场反应所需抵抗人工边界物理元件的结点力，第3项表示产生内行场反应所需抵抗近场介质的结点力。地震动输入时，通过地表加速度时程进行积分反演，求出内行场位移时程和速度时程，确定人工边界表面应力时程，通过编写程序即可实现黏弹性边界的地震动输入。图5所示为相应的运行程序流程，计算程序的合理性与正确性已在文献[14]进行了详细论证。

图4　三维黏弹性人工边界条件Fig. 4 Three-dimensional viscoelastic artificial boundary

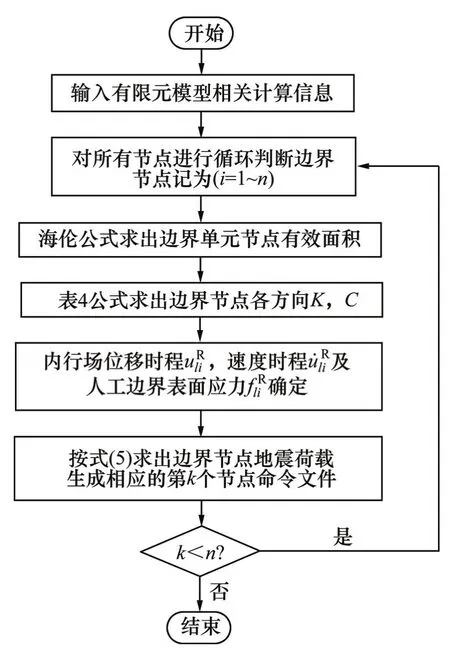
图5　黏弹性边界程序流程图Fig. 5 Program flow chart of viscoelastic boundary

3　桩−土−结构相互作用隔震网壳结构地震响应

3.1结构模型

根据文献建立桩−土−结构相互作用下的3向单层网格柱面网壳结构[15]，网壳跨度为20 m，长度为30 m，矢跨比为1/5，屋面恒载为0.5 kN/m2，网壳斜杆外径×壁厚为165 mm×5 mm，其他杆外径×壁厚为102 mm×4 mm；柱网为20 m×10 m，柱高为6 m，钢柱外径×壁厚为600×40 mm；钢材选用Q235，密度为7 800 kg/m3，泊松系数为0.3，弹性模量为2.06×1011Pa。基础采用承台全桩基础，承台断面长×宽为4 m×4 m，承台厚度为1 m，全桩长为16 m，采用2×2根长度为15 m的钻孔灌注桩，混凝土采用C30；采用Mohr−Coulomb条件作为土体的本构计算模型，弹性模量E=250 MPa，泊松系数取为0.3，阻尼比取为0.10，密度为2 000 kg/m3，黏聚力为19 kN，摩擦角为32°，膨胀角为25°；桩与土之间的摩擦因数为0.3。

3.2有限元建模

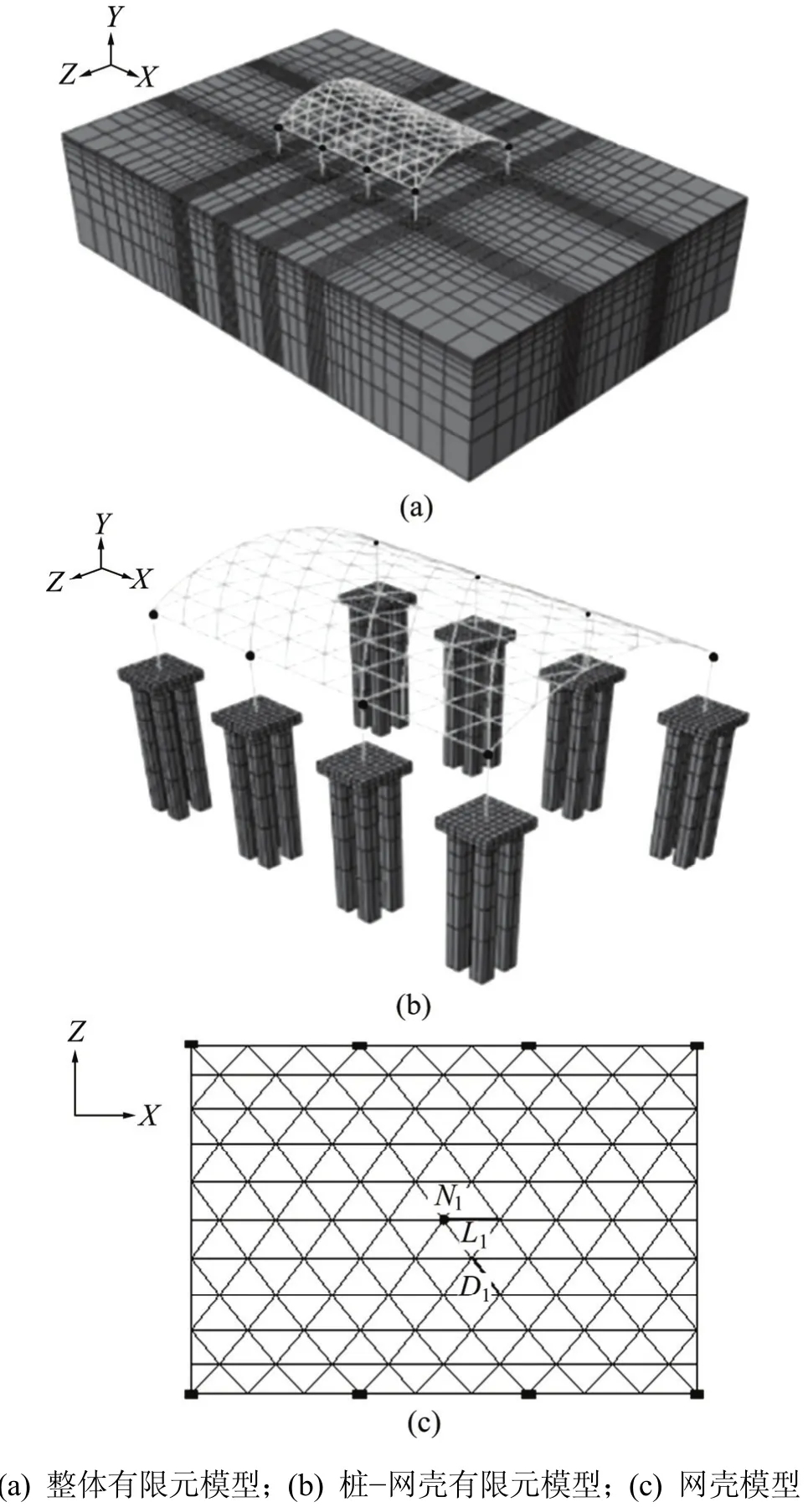
图6　有限元计算模型Fig. 6 Finite element calculation model

采用ABAQUS软件建立有限元模型如图6所示，由FPB3000试验可知新型摩擦摆支座的三维数值模拟是合理的，因此，根据所建立的网壳结构设计与结构相符的FPB100支座，符号“▃”表示支座，施加于柱顶，此支座的竖向承载力为100 kN，竖向抗拔力为20 kN，径向允许位移为70 mm，数值模拟所得的滞回曲线如图7所示。依据FPB100的滞回曲线，将支座进行双线性简化，分析可得FPB100支座摩擦因数为0.102，满足试验所得的范围0.096～0.107，初始刚度K1=7.825×106N/m，屈服刚度K2=1.834×105N/m，以CONNECTOR单元实现双线性模拟支座，下部土体和桩基均采用实体单元C3D8R模拟，上部网壳结构以BEAM单元模拟。

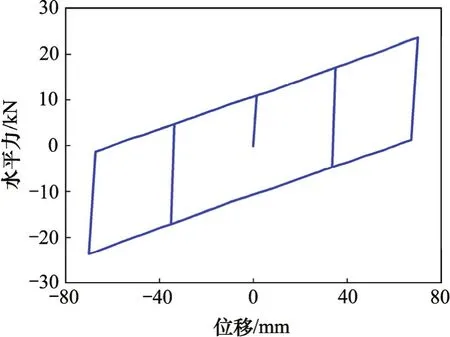
图7　FPB100滞回曲线Fig. 7 Hysteresis loop of FPB100

3.3输入地震动参数

为研究桩−土−结构相互作用下新型抗拔摩擦摆支座对单层柱面网壳结构地震响应的影响及地震波输入的空间效应问题，今选取日本Kobe波及美国Northridge波加速度记录作为地震动输入，对PSSI和PSSII体系下单层柱面网壳结构的地震响应进行分析。地震动截取能反映波动特性的前20 s时程进行输入[16]，并将输入加速度峰值调整为2.2 m/s2，输入地震动的加速度时程曲线如图8所示。

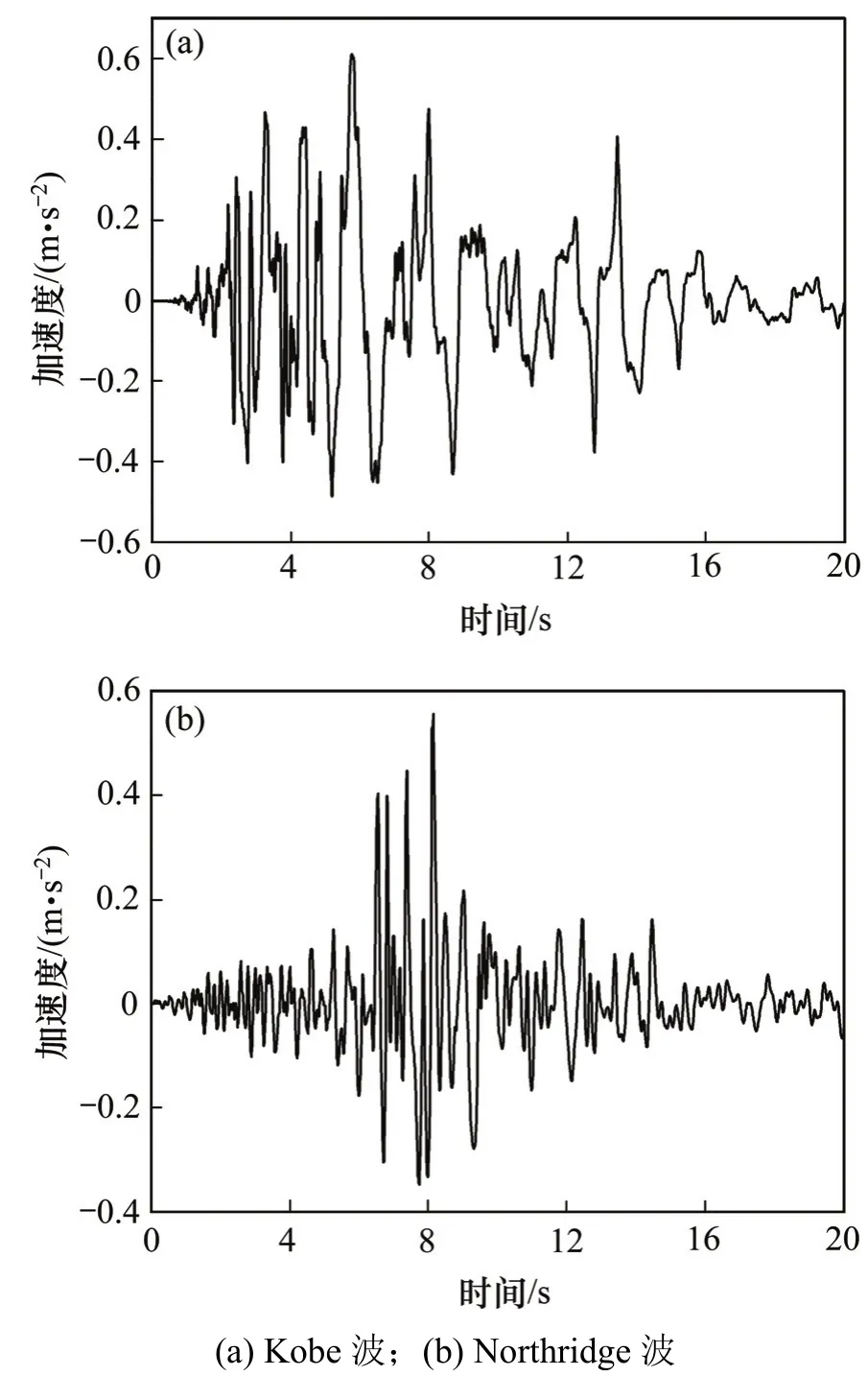
图8　不同地震波加速度时程曲线Fig. 8 Acceleration time history curves of different waves

3.4PSSI下新型抗拔摩擦摆支座对单层柱面网壳结构地震响应的影响

图9所示为在Kobe波和Northridge波作用下，网壳结构中心节点(N1)在PSSI模型和PSSII型体系下的节点加速度、节点位移沿X方向的时程曲线。图10所示为在Kobe波和Northridge波作用下，网壳结构纵向直杆(L1)和斜杆(D1)的杆件内力时程曲线。表5所示为在不同地震波作用下，PSSI体系与PSSII体系中所有杆件中节点加速度最大值与杆件内力最大值比较。由图9、图10和表5可以看出：在Kobe波和Northridge波作用下，PSSII模型体系的节点加速度明显较在PSSI模型体系减小，加速度衰减50%～60%，表明新型竖向铜基面抗拔摩擦摆支座对网壳结构起到了明显的隔震效果。PSSII模型体系的节点位移明显较在PSSI模型体系增大，表明新型竖向铜基面抗拔摩擦摆支座使得PSSII体系较PSSI体系变柔，从而致使节点位移增加。PSSII模型体系中网壳结构斜杆和纵向杆件的内力明显减小，内力最大值衰减50%～80%，表明新型竖向铜基面抗拔摩擦摆支座使网壳结构杆件的内力减小，达到了理想的隔震效果，有利于网壳结构抗震，应当在工程中推广利用。

在不同地震波作用下，抗拔摩擦摆支座使网壳结构的节点加速度、杆件内力衰减程度和节点位移的增大程度不同，这表明地震波频谱特性对抗拔摩擦摆支座的隔震效应有着不可忽略的影响。

3.5地震波输入角度对PSSII体系地震响应影响

从波传播的物理机制方面来讲，由于地震波的入射角度(地震波入射方向与竖向的夹角)不同，使地震波在场地中发生不同的反射和折射，使地表各点的地震波发生不同程度的叠加，引起结构中各支承所受的激励不同，致使结构各点振动的相位和振幅产生差异[17]，成为影响大跨空间结构地震响应的一个重要因素。因此，本节探讨Kobe波和Northridge波在不同角度入射下，PSSII网壳结构中所有节点的加速度最大值及所有网壳杆件中内力最大值随入射角的变化情况。

图9　网壳结构节点N1加速度和位移时程曲线Fig. 9 Node N1acceleration and displacement time history curves of cylindrical reticulated shell

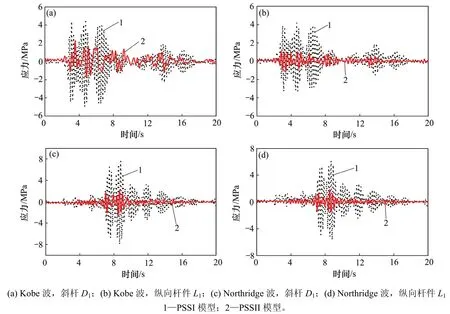
图10　网壳结构斜杆和纵向杆件应力时程曲线Fig. 10 Stress time history curves of diagonal and longitudinal member of cylindrical reticulated shell

图11所示为在Kobe波和Northridge波作用下，网壳所有节点中水平(X向)、竖向(Z向)加速度最大值随入射角度变化情况。图12所示为在Kobe波和Northridge波作用下，网壳所有斜杆、纵向直杆中内力最大值随入射角度变化情况。由图11和图12可以看出：在不同地震波作用下， PSSII体系网壳节点竖向加速度最大值随入射角度增大呈减小的趋势，在入射角为50°左右出现明显的拐点；PSSII体系网壳节点水平加速度最大值随着入射角度的增大呈先增大后减小的趋势，在50°左右出现最大值。PSSII体系中网壳的斜杆和纵向直杆内力最大值随着入射角度的增大呈减小趋势，在45°～60°之间衰减缓慢。PSSII体系中网壳节点加速度最大值、杆件内力因地震波差异而不同，这是由地震波的频谱特性引起的。

研究表明地震波斜入射下PSSII体系地震响应与地震波的频谱特性有关；PSSII体系网壳节点加速度最大值未必在地震波垂直入射时最大，入射角度45°～60°是一重要的考虑区间。

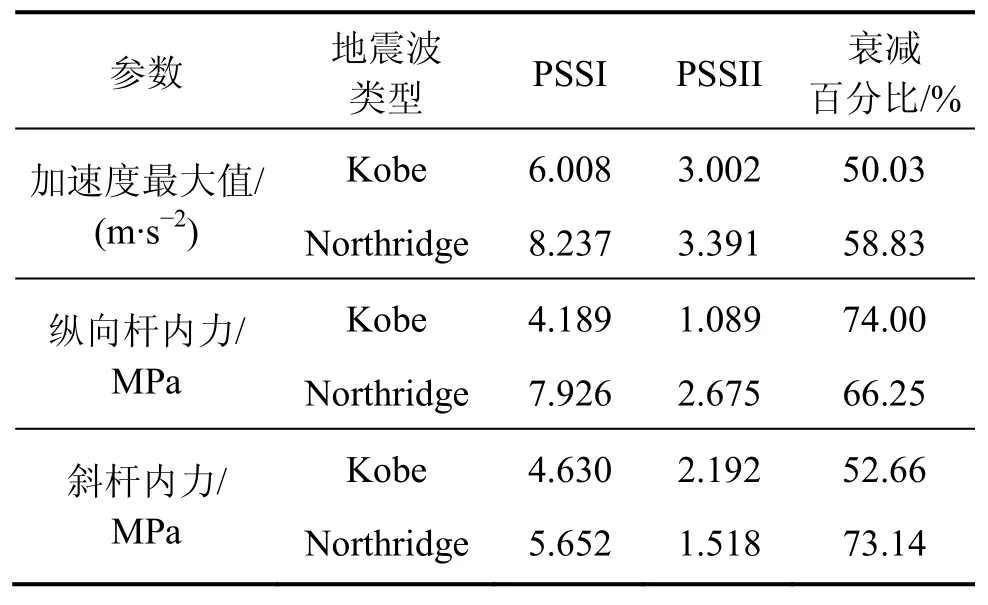
表5　不同体系下节点加速度最大值与杆件内力最大值比较Table 5 Comparison of maximum acceleration and internal force of members in various structural system

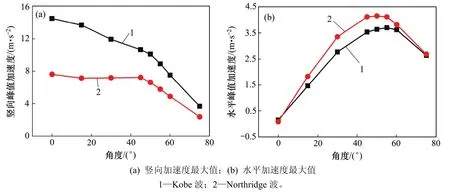
图11　网壳节点加速度最大值与入射角度的关系Fig. 11 Relationship between the maximum acceleration of shell node and incident angle

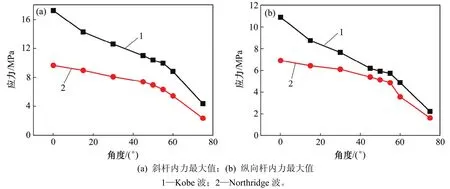
图12　网壳斜杆内力与入射角度关系Fig. 12 Relationship between the maximum stress of shell members and incident angle

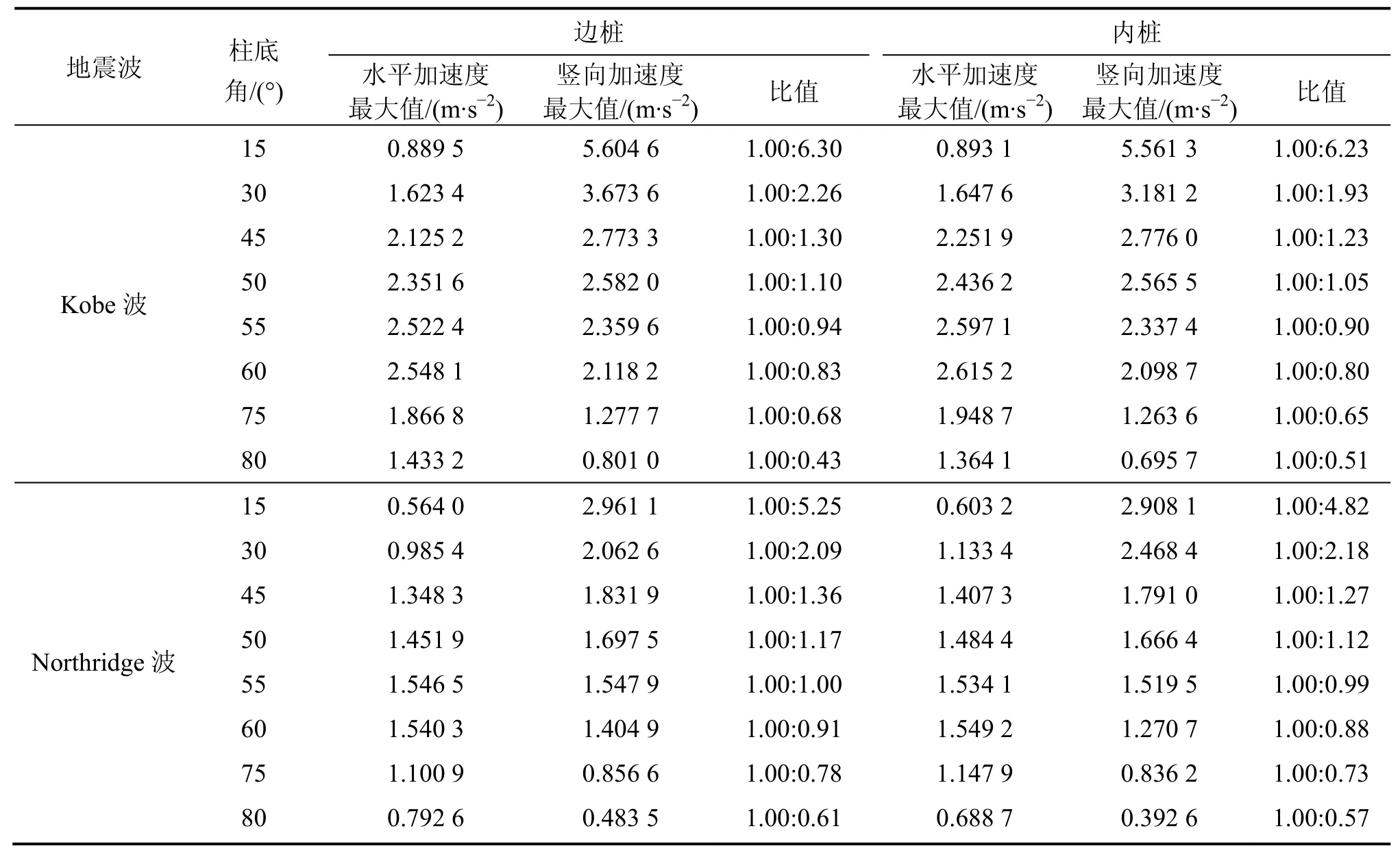
表6　PSSII体系柱底水平加速度最大值与竖向加速度最大值的比值Table 6 Ratio between horizontal maximum acceleration and vertical maximum acceleration of PSSII column base

3.6地震波输入的空间效应问题

GB 50011—2010“建筑抗震设计规范”[18]第5.1.2条规定：结构采用三维空间模型等需要双向(2个水平)或三向(2个水平和1个竖向)地震波输入时，其加速度最大值通常按照1.00(水平):0.85(水平):0.65(竖向)的比例调整进行地震动输入，按此规定水平与竖向加速度最大值的比例为1.00:0.65或1.00:0.76。本文研究了考虑在PSSI作用下隔震网壳结构在不同地震动入射角度下边桩、内桩柱底水平加速度最大值和竖向加速度最大值的比值，探讨地震波输入的空间效应问题。表6所示为在不同角度地震波入射下，PSSII体系柱底水平加速度最大值与竖向加速度最大值的比值。由表6可以看出：在Kobe波和Northridge波作用下，入射角度在55°～80°之间结构体系柱底的水平加速度最大值与竖向加速度最大值的比例大致符合“建筑抗震设计规范”规定1.00 (水平):0.85(水平):0.65(竖向)的比例。地震波入射角在0°～50°和80°～90°时，柱底的水平加速度最大值与竖向加速度最大值的比例明显不符合“建筑抗震设计规范”规定。柱底的加速度最大值因地震波的不同而异，与地震波频谱特性有关。

研究表明，“建筑抗震设计规范”规定地震波输入时，水平与竖向的加速度最大值按比例1.00:0.65或1.00:0.76输入并非完全合理的，水平和竖向地震波输入比例与地震波的入射角度有关，当地震波入射角度为55°～80°时，可按规范规定进行地震波输入；当不在此范围时，不宜按照规范规定进行地震波输入，应当考虑地震波入射的空间效应。

4　结论

1) 在地震作用下，铜基面抗拔摩擦摆支座使桩−土−结构作用下的网壳结构的节点加速度最大值衰减50%～60%，网壳杆件的内力衰减50%～80%，起到了明显的隔震效果。

2) 在不同地震波作用下，同时考虑桩−土−结构相互作用和新型竖向抗拔摩擦摆支座隔震下网壳结构的节点加速度、杆件内力衰减程度和节点位移的增大程度不同，这表明地震波的频谱特性对抗拔摩擦摆支座的隔震效应有着不可忽略的影响。

3) 地震波的入射角度对PSSII体系地震响应有着重要影响，PSSII体系网壳节点加速度最大值未必在地震波垂直入射时最大，入射角度45°～60°是重要的响应范围。

4)“建筑抗震设计规范”规定地震波输入时，水平与竖向的加速度最大值按比例1.00:0.65或1.00:0.76输入并非完全合理的，水平和竖向地震波输入比例应与地震波的入射角度有关，当地震波入射角度为55°～80°时，可按规范规定进行地震波输入，当不在此范围时，不宜按照规范规定进行地震波输入，应当考虑地震波的空间效应。

[1] 朱黎蓬, 张书, 姜千君. 振动控制在大跨度空间结构中的应用概述[J]. 山东建筑大学学报, 2009, 24(5): 472−476. ZHU Lipeng, ZHANG Shu, JIANG Qianjun. Application of vibration control in long span spatial structures [J]. Journal of Shandong Jianzhu University, 2009, 24(5): 472−476.

[2] 薛素铎, 蔡炎城, 李雄彦, 等. 被动控制技术在大跨空间结构中的应用概况[J]. 世界地震工程, 2009, 25(3): 25−33. XUE Suduo, CAI Yancheng, LI Xiongyan, et al. The present situation application of passive control technology in long span spatial structures[J]. World Earthquake Engineering, 2009, 25(3): 25−33.

[3] YAO J T. Concept of structure control[J]. Journal of Structural Division, ASCE, 1972, 98(7): 1567−1574.

[4] 肖建春, 聂建国, 马克俭, 等. 预应力网壳结构中加劲板式橡胶支座的计算模型及设计[J]. 建筑结构学报, 2001, 22(3): 54−59. XIAO Jianchun, NIE Jianguo, MA Kejian, et al. Mechanical model and design method of rubber bearing in prestressed reticulated shells[J]. Journal of Building Structure, 2001, 22(3): 54−59.

[5] 施卫星, 孙黄胜, 李振刚, 等. 上海国际赛车场新闻中心高位隔震研究[J]. 同济大学学报(自然科学版), 2005, 33(12): 1576−1580. SHI Weixing, SUN Huangsheng, LI Zhengang, et al. High-position seismic isolation of press center at Shanghai international circuit[J]. Journal of Tongji University (Natural Science), 2005, 33(12): 1576−1580.

[6] 徐庆阳, 李爱群, 张志强, 等. 某大跨网架结构屋盖隔震整体分析[J]. 工程抗震与加固改造, 2007, 29(6): 20−24. XU Qingyang, LI Aiqun, ZHANG Zhiqiang, et al. Roof-isolation integral analysis of one long-span space truss structure[J]. Earthquake Resistant Engineering and Retrofitting, 2007, 29(6): 20−24.

[7] 陆伟东, 刘伟庆, 吴晓飞, 等. 昆明新国际机场航站楼A区结构模型振动台试验研究[J]. 建筑结构学报, 2011, 32(6): 27−33. LU Weidong, LIU Weiqing, WU Xiaofei, et al. Shaking table test of terminal a structure of Kunming international airport[J]. Journal of Building Structure, 2011, 32(6): 27−33.

[8] 朱忠义, 束伟农, 柯长华, 等. 减隔震技术在航站楼大跨结构中的应用[J]. 空间结构, 2012, 18(1): 17−24. ZHU Zhongyi, SHU Weinong, KE Changhua, et al. Application of the seismic isolated and mitigation technologies in large span structures of airport terminal buildings[J]. Spatial Structures, 2012, 18(1): 17−24.

[9] LI Xiongyan, XUE Suduo, CAI Yancheng. Three-dimensional seismic isolation bearing and its application in long span hangars[J]. Earthquake Engineering and Engineering Vibration, 2013, 12(1): 56−65.

[10] 杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件[J]. 力学学报, 2006, 38(1): 49−56. DU Xiuli, ZHAO Mi, WANG Jinting. A stress artificial boundary in FEA for near-field wave [J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 49−56.

[11] 刘云贺, 张伯艳, 陈厚群. 拱坝地震输入模型中黏弹性边界与黏性边界的比较[J]. 水利学报, 2006, 37(6): 758−763. LIU Yunhe, ZHANG Boyan, CHEN Houqun. Comparison of spring-viscous boundary with viscous boundary for arch dam seismic input model[J]. Journal of Hydraulic Engineering, 2006, 37(6): 758−763.

[12] 刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域黏弹性人工边界[J]. 工程力学, 2005, 22(6): 46−51. LIU Jingbo, WANG Zhenyu, DU Xiuli, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems[J]. Engineering Mechanics, 2005, 22(6): 46−51.

[13] 赵建峰, 杜修力, 韩强, 等. 外源波动问题数值模拟的一种实现方式[J]. 工程力学, 2007, 24(4): 52−58. ZHAO Jianfeng, DU Xiuli, HAN Qiang, et al. An approach to numerical simulation for external source wave motion[J]. Journal of Mechanics, 2007, 24(4): 52−58.

[14] 刘毅, 薛素铎, 李雄彦. 土−结构动力相互作用下网架结构动力性能研究[J]. 振动与冲击, 2014, 33(10): 23−30. LIU Yi, XUE Suduo, LI Xiongyan. An analysis of grid structure dynamic performance considering soil-structure dynamic interaction[J]. Journal of Vibration and Shock, 2014, 33(10): 23−30.

[15] 杨大彬, 张毅刚, 吴金志. 纵边落地支承单层柱面网壳强震倒塌机理及参数分析[J]. 世界地震工程, 2011, 27(4): 143−148. YANG Dabin, ZHANG Yigang, WU Jinzhi. Collapse mechanism and parameter analysis of single-layer cylindrical latticed shell with longitudinal edge supports on ground under severe earthquake[J]. Word Earthquake Engineering, 2011, 27(4): 143−148.

[16] 曹资, 薛素铎, 王雪生, 等. 空间结构抗震分析中的地震波选取与阻尼比取值[J]. 空间结构, 2008, 14(3): 3−8. CAO Zi, XUE Suduo, WANG Xuesheng, et al. Selection of earthquake waves and values of damping ratio for space structures in aseismic analysis[J]. Spatial Structure, 2008, 14(3): 3−8.

[17] 潘旦光, 楼梦麟, 范立础. 多点输入下大跨度结构地震反应分析研究现状[J]. 同济大学学报, 2001, 29(10): 1213−1219. PAN Danguang, LOU Menglin, FAN Lichu. Status of seismic response analysis of long-span structures under multiple support excitations[J]. Journal of Tongji University, 2001, 29(10): 1213−1219.

[18] GB 50011—2010, 建筑抗震设计规划[S]. GB 50011—2010, Code for seismic design of buildings[S].

(编辑 刘锦伟)

Effect of a new friction pendulum bearing on seismic response of single-layer cylindrical reticulated shell considering pile-soil-structure interaction

LIU Yi1,2, XUE Suduo1, PAN Kejun3, LI Xiongyan1
(1. School of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China; 2. CRRC Construction Engineering Co. Ltd., Beijing 100078, China; 3. Homedale Architects, Beijing 100045, China)

Based on the numerical and experimental study of a new type friction pendulum bearing (FPB) with stainless steel interfaces and anti-uplift device, the new bearing was simplified with the bilinear model. A single-layer cylindrical reticulated shell model was established in consideration of the pile−soil−structure interaction and isolation (PSSII) by integral finite element method combined with theories of pile−soil−structure interaction and viscoelastic boundary. The new bearing impacts on the seismic response of single-layer cylindrical reticulated shell were discussed, as well as the spatial effect of input seismic wave. The results show that the nodal peak acceleration of the shell decrease by 50%−60%, and the internal force of the structural members decrease by 50%−80%. The effect of spectrum characteristics of seismic wave on the isolation effects of the new bearings cannot be ignored. The peak acceleration of the PSSII systemmay not appear at the maximum value in the vertical incident of the seismic wave, and the incident angle 45°−60° is an important range which should be considered carefully. The national standard should be followed in seismic calculation when the incident angle of seismic wave is between 55° and 80°. On the other hand, the code should not be followed, and the spatial effect of seismic wave should be considered independently.

single-layer cylindrical reticulated shell; pile−soil−structure interaction; vertical anti-uplift friction pendulum bearing; seismic response; incident angle isolation

TU311.3

A

1672−7207(2016)03−0967−10

10.11817/j.issn.1672-7207.2016.03.033

2015−03−02；

2015−05−17

国家自然科学基金资助项目(51078010，51278008)；北京市自然科学基金资助项目(8112005) (Projects(51078010, 51278008) supported by the National Natural Science Foundation of China; Project(8112005) supported by the Beijing Municipal Natural Science Foundation)

刘毅，博士，工程师，从事大跨空间结构、地下空间结构抗震方面研究；E-mail: chrisbin@emails.bjut.edu.cn