空间隔膜压缩机的可靠性评估方法

邵立民 杨海峰 赵新攀

（中国空间技术研究院载人航天总体部，北京 100094）

空间隔膜压缩机的可靠性评估方法

邵立民 杨海峰 赵新攀

（中国空间技术研究院载人航天总体部，北京 100094）

针对目前没有适合空间隔膜压缩机可靠性评估方法的问题，文章以无失效贝叶斯可靠性评估方法为基础，综合利用配分布曲线法、零部件失效率函数特性、可靠性预计数据，提出了适用于空间隔膜压缩机可靠性评估方法，通过计算实例证明了该方法能够解决空间隔膜压缩机小子样、无失效子样可靠性评估问题，可为同类产品可靠性评估提供参考。

空间隔膜压缩机；小子样；无失效子样；可靠性评估

1 引言

推进剂在轨补给技术是实现大型航天器长寿命运行的必要条件，俄罗斯的礼炮号、和平号空间站和在轨的“国际空间站”等均实施了多次推进剂在轨补给［1］。目前的推进剂补给体制主要有压气机体制和泵输送体制，而隔膜压缩机是上述两种补给体制的核心设备。隔膜压缩机靠金属隔膜在膜腔中往复运动来压缩和输送气体或液体工质［2］。

空间隔膜压缩机具有可靠性高、结构复杂、在轨不可维修等特性，一般要求具有10年以上寿命和高可靠性，而空间隔膜压缩机昂贵的价格（百万元量级）决定了可靠性验证试验的样本量不可能太多，而且试验结果往往出现无失效情况。常规的机械产品可靠性评估方法［3］需要大量的试验子样，特别是需要出现失效子样，试验成本很高，不适用于空间隔膜压缩机的可靠性评估。

Martz H.F.、Waller R.A.以及茆诗松、韩明等人针对无失效数据产品提出了可靠性评估方法并结合一般实例进行了分析计算［4－6］，其方法具有借鉴意义。但空间隔膜压缩机是包含机身、减速器、膜片、轴承、阀门、电机、活塞、曲轴、膜腔等多种机电产品的复杂集合体，国内外尚无空间隔膜压缩机的可靠性评估方法。因此，有必要根据空间隔膜压缩机的结构特征和小样本、无失效可靠性试验特点提出适合于工程应用的可靠性评估方法。

本文首先建立了空间隔膜压缩机可靠性框图模型和可靠性数学模型，并分析了压缩机组成零部件寿命末期失效模式和寿命分布函数。其次，在配分布曲线法基础上，引入零部件失效率函数特性和可靠性预计信息，建立了无失效贝叶斯可靠性评估模型。最后，利用算例验证了本文方法的可行性。

2 空间隔膜压缩机的可靠性模型

空间隔膜压缩机工作原理如图1所示。

图1 空间隔膜压缩机原理图Fig.1 Principle sketch of spacial diaphragm compressor

空间隔膜压缩机各个零部件失效模式相互独立，组成可靠性串联系统，可靠性框图如图2所示。图1中，曲柄、活塞、膜腔等强度裕度在2以上，为简化计算，上述零部件不体现在图2中。根据图2建立空间隔膜压缩机串联系统可靠性数学模型为

式中：Ri为空间隔膜压缩机各个零部件的可靠度。

图2 空间隔膜压缩机可靠性框图Fig.2 Reliability frame of spacial diaphragm compressor

分析空间隔膜压缩机各个零部件主要失效模式，并根据文献［7－10］确定了各个零部件寿命分布函数，见表1。

表1 空间隔膜压缩机零部件寿命分布函数Table 1 Life distribution function for componentsof spacial diaphragm compressor

3 空间隔膜压缩机可靠性评估方法

空间隔膜压缩机可靠性评估方法的主要步骤如图3所示。

图3 空间隔膜压缩机可靠性评估主要步骤Fig.3 Process of reliability assessment of spacial diaphragm compressor

3.1 获取无失效定时截尾试验数据

从同一批次空间隔膜压缩机中随机选取n台产品并分成k组进行试验，各组样品数量分别为n1，n2，…，nk。试验过程中记录定时截尾试验时间t1，t2，…，tk，且t1＜t2＜…＜tk，每一试验时间ti参试产品无一失效。

由ti和si构成一组无失效数据，表示为：（ti，si），且si＝ni＋ni＋1＋…＋nk，si表示在定时截尾时刻ti前未失效样品总数。

3.2 建立无失效贝叶斯可靠性评估模型

空间隔膜压缩机可靠性评估的关键是试验子样无失效情况的处理。首先建立试验子样存在失效情况的似然函数，对应每个截尾时刻t1，t2，…，tk的累积失效率记为p1，p2，…，pk。在已知ti时刻的累积失效率pi的条件下，由二项式分布定理可知，si件样本中有ri件产品失效，pi的似然函数为［11］

针对本文提出的无失效子样问题，当第i组产品定时截尾试验时间为ti时，发现试验产品无失效，则ri＝0，式（2）转变为

利用贝叶斯定理，取π（pi）作为pi的先验分布，可得pi和si的联合分布为

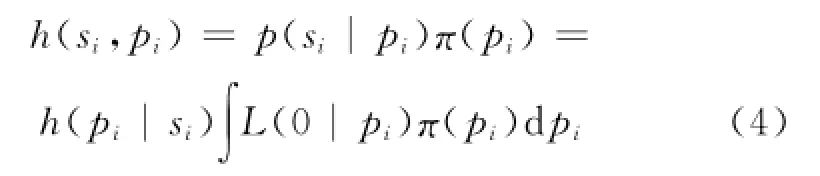
可得参数pi在样本si条件下的后验分布密度函数为

式（5）中集合了总体、样本和先验等三种关于pi的全部信息，因此对pi的评估更加有效、合理，这也是航天行业广泛使用贝叶斯法进行有限子样产品可靠性评估的原因。

在平方损失下，用后验均值E［h（pi｜si）］作为pi的贝叶斯估计为

根据贝叶斯定理基本假设及文献［11］的建议，如果在试验前对pi不是很了解，但由于空间隔膜压缩机试验样本均无失效，可以认为在（0，ti）时间内的失效概率pi是个极小值，即pi是小于1的某个值λi。那么pi先验分布认为是均匀分布U（0，λi）的假设是合理的，其中0≤λi≤1，而λi可由专家建议或可靠性预计信息等先验信息确定。

文献［12－13］采用配分布曲线法，在pi先验分布是均匀分布U（0，λi）的基础上，利用威布尔分布、对数正态分布产品失效概率F（t）是t的凹函数性质作为总体分布信息，即

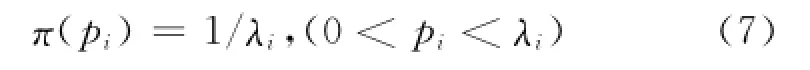
将式（7）代入式（5）、式（6）得到累积失效率pi的贝叶斯估计为

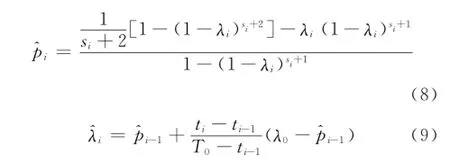
式中：λ0为被评估产品在工作T0时刻后的总体样本失效率，且T0＞tk。

对于电机等寿命服从指数分布的产品，指数分布失效率F（t）如图4所示，在样本试验时间t＜1/λ（平均寿命）时，指数分布失效率F（t）为试验时间t的凸函数。本文在先验分布为均匀分布基础上，利用指数分布失效率曲线为凸函数的特性作为先验信息。

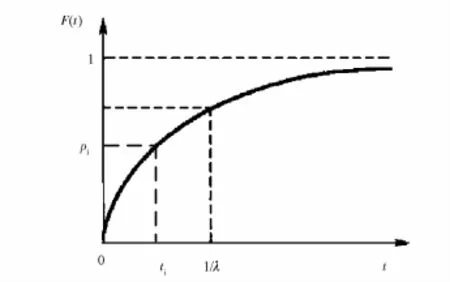
图4 指数分布失效概率F（t）随试验时间t的变化Fig.4 Failure probability of exponential distribution F（t）versus test time t

可以选取一个适当大的时间T0（＞tk），通过专家建议或可靠性预计回答“产品寿命T超过T0的可能性至少有多少”。若得到的结果为（1－λ0），就意味着产品工作到T0时刻的失效概率p0不会超过λ0，即p0的上限为λ0。需要指出的是T0的选取不应超出tk过多，本文建议T0≤tk＋（tk－tk－1）。

根据指数分布特性，由于当t＜1/λ时，F（t）是t的凸函数，由于p0＜λ0＜λ，则t1＜t2＜…＜T0＜1/λ，由凸函数性质可知

式中：t′＜t1，p′＝P（T＜t′）。当试验样本母体分布满足指数分布时，p1，p2，…，pk应满足上式。

当产品多次试验均无失效，因此t′＝0时，失效概率p′很小，可近似取为0。由于ti－1＜ti，则pi－1＜pi，由凸函数的性质可知

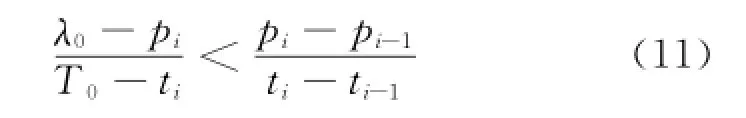
式中：λ0为被评估产品在工作T0时刻后的总体样本失效率，且T0＞tk。

由于pi应满足pi－1＜pi＜λi，即pi的先验分布为均匀分布U（pi，λi），其中

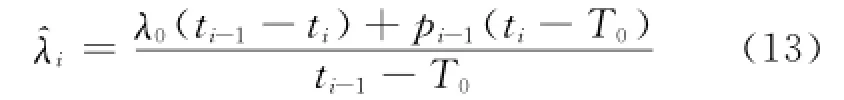
将π（pi）～U（pi，λi）代入式（5）、式（6）得pi的

贝叶斯估计为

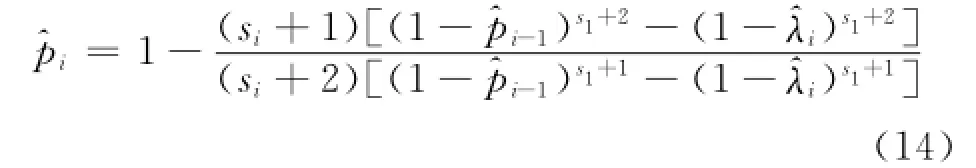
3.3 零部件可靠性预计

式（9）和式（13）中的λ0属于先验分布中的超参数。文献［11－13］采用了专家经验法，请专家回答“产品寿命T超过T0的可能性（1－λ0）至少有多少”。考虑到空间隔膜压缩机为新研产品，专家经验往往无从获取或者专家的经验过于保守（例如专家认为T0时刻后，被试产品的工作正常的概率大于0.5），本文采用可靠性预计的方法回答T0时刻失效率λ0。

3.4 零部件和整机可靠性评估计算

1）对数正态分布零部件可靠性评估

机身、膜片、减速器等零部件在工作时间t后的可靠度为R（t）＝Φ［μ－ln（t/σ）］，待估参数由式（15）计算得到。

2）威布尔分布零部件可靠性评估

曲轴轴承、调压阀、进气阀、排气阀、配油阀等零部件在工作时间t后的可靠度为R（t）＝exp［－（t/η）β］，待估参数由式（16）计算得到。

3）指数分布零部件可靠性评估

电机等零部件在工作时间t后的可靠度为R（t）＝exp（－λt），待估参数由公式（17）计算得到。

4）空间隔膜压缩机整机可靠性评估

根据上述方法得到空间隔膜压缩机10个零部件连续工作t的可靠度，代入式（1）可计算出空间隔膜压缩机在工作t后的可靠度RS。

4 空间隔膜压缩机可靠性评估算例

利用算例检验所提出的空间隔膜压缩机可靠性评估方法的可行性。

1）获取无失效试验数据

在某次空间隔膜压缩机研制任务中，用户提出其任务寿命不小于800h，投入10台产品（分成5组、每组2台）开展可靠性验证试验，在定时截尾试验时间t1＝1500h，t2＝1750h，t3＝2000h，t4＝2250h，t5＝2500h时，参试的10台产品均未失效。获得的压缩机机身等10个零部件的无失效试验数据（ti，si）均为（1500，10）、（1750，8）、（2000，6）、（2250，4）、（2500，2），且n1＝n2＝n3＝n4＝n5＝2。

2）零部件可靠性预计

根据空间隔膜压缩机各个零部件详细设计参数，以及文献［7］对对数正态分布的疲劳失效结构产品、文献［8］对指数分布的电动机、文献［9］和文献［15］对威布尔分布的滚动轴承、文献［10］和［16］对威布尔分布的阀门可靠性预计方法可以得到表2中各个零部件工作T0＝2550h后的失效率λ0，见表2第2列数据。

3）计算累积失效率和待估参数

将机身的无失效数据（ti，si）～（1500，10）、（1750，8）、（2000，6）、（2250，4）、（2500，2）和T0＝2550h后的失效率预计值λ0＝0.006 418代入式（8）和式（9）得到累积失效率为（0.001 876， 0.001 473，0.001 505，0.001 864，0.002 824）。将（ti，si）和代入式（15）得到可靠度评估计算模型中待估参数

同样，将膜片、减速度等零部件的无失效数据ti、 ni和代入式（15），将轴承1/2、调压阀、进气阀、排气阀、配油阀的ti、ni和代入式（16），得到上述零部件的可靠度评估计算模型的待估参数值，见表2第4列数据。

将电机的无失效数据（ti，si）～（1500，10）、（1750，8）、（2000，6）、（2250，4）、（2500，2）和T0＝ 2550h后的失效率预计值λ0＝0.007 707代入式（13）和式（14）得到累积失效率为（0.002 250， 0.002 898，0.003 648，0.004 570，0.005 876）。将ti、ni和代入式（15）得到电机可靠度评估计算模型的待估参数值。

4）计算零部件和整机可靠度评估值

上述计算过程验证了本文方法的可行性，并且在可靠性预计基础上通过累积无失效试验子样，可靠性评估指标相对略微增加，符合实际情况。

表2 空间隔膜压缩机零部件可靠性评估Table 2 Reliability estimation of components for spacial diaphragm compressor

5 结束语

本文以无失效贝叶斯可靠性评估为基础，利用配分布曲线方法、失效分布函数特性，提出了空间隔膜压缩机可靠性评估方法，通过引入可靠性预计信息，克服了专家经验法等主观性验前信息的不足。通过计算实例证明，本文方法能够解决空间隔膜压缩机可靠性评估中的小子样、无失效难题。

对于其他复杂空间机械产品的可靠性评估，若产品零部件寿命分布函数为威布尔、对数正态、指数分布函数，且产品定时截尾试验数据具有小子样无失效的特点，也可参考本文方法。

（

）

［1］江铭伟.俄罗斯空间站推进剂补加程序分析［J］.火箭推进，2013，39（4）：8－12 Jiang Mingwei.Analysis of propellant refueling program for Russian space station［J］.Journal of Rocket Propulsion，2013，39（4）：8－12（in Chinese）

［2］David J Chato.Technologies for refueling spacecraft on－orbit，TM－2000－210476［R］.Washington D.C.：NASA，2000

［3］周正伐.航天可靠性工程［M］.北京：中国宇航出版社，2007 Zhou Zhengfa.Space flight reliability engineering［M］.Beijing：China Astronautics Press，2007（in Chinese）

［4］Martz H F，Waller R A.A Bayesian zero－failure（BAZE）reliability demonstration testing procedure［J］.Journal of Quality Technology，1979，11（3）：128－138

［5］茆诗松，王玲玲.威布尔分布场合无失效数据的可靠性分析［J］.应用概率统计，1996，12（1）：95－107 Mao Shisong，Wang Lingling.Reliability analysis for Weibull zero failure data［J］.Chinese Journal of Applied Probability and Statistics，1996，12（1）：95－107（in Chinese）

［6］韩明.无失效数据可靠性参数的综合估汁［J］.数学理论与应用，2000，20（3）：36－44 Han Ming.The synthesize estimation of reliability parameter of zero－failure data［J］.Mathematical Theory and Application，2000，20（3）：36－44（in Chinese）

［7］吴波，黎明发.机械零件与系统可靠性模型［M］.北京：化学工业出版社，2003Wu Bo，Li Mingfa.Mechanical parts and system reliability model［M］.Beijing：Chemical Industry Press，2003（in Chinese）

［8］中国标准出版社.GJB/Z 299C－2006电子设备可靠性预计手册［S］.北京：中国标准出版社，2006：154－155 China Standardization Press.GJB/Z 299C－2006Reliability prediction handbook for electronic equipment［S］.Beijing：China Standardization Press，2006：154－155（in Chinese）

［9］中国国家标准化管理委员会.GB/T 24607－2009滚动轴承寿命与可靠性试验及评定［S］.北京：中国国家标准化管理委员会，2010 Standardization Administration of the People’s Republic of China.GB/T 24607－2009Rolling bearings－Test and assessment for life and reliability［S］.Beijing：Standardization Administration of the People’s Republic of China，2010（in Chinese）

［10］Marvin Rausand，Join Vatn.Reliability modeling of surface controlled subsurface safety valves［J］.Reliability Engineering and System Safety，1998，61：159－166

［11］茆诗松，罗朝斌.无失效数据的可靠性分析［J］.数理统计与应用概率，1989，4（4）：489－506 Mao Shisong，Luo Chaobin.Reliability analysis of zero－failure data［J］.Mathematical Statistics and Applied Probability，1989，4（4）：489－506（in Chinese）

［12］张志华，姜礼平.正态分布场合下无失效数据的统计分析［J］.工程数学学报，2005，22（4）：741－744 Zhang Zhihua，Jiang Liping.Statistical analysis of zero－failure data based on the normal distribution［J］.Chinese Journal of Engineering Mathematics，2005，22（4）：741－744（in Chinese）

［13］刘海涛，张志华.威布尔分布无失效数据的Bayes可靠性分析［J］.系统工程理论与实践，2008，28（11）：103－108 Liu Haitao，Zhang Zhihua.Bayesian reliability analysis of Weibull zero failure data［J］.Systems Engineering Theory ＆Practice，2008，28（11）：103－108（in Chinese）

［14］赵宇.可靠性数据分析［M］.北京：国防工业出版社，2011 Zhao Yu.Data analysis of reliability［M］.Beijing：National Defence Industry Press，2011（in Chinese）

［15］朱德馨，刘宏昭.极小样本下高速列车轴承的可靠性评估［J］.中南大学学报（自然科学版），2013，44（3）：963－969 Zhu Dexin，Liu Hongzhao.Reliability evaluation of high－speed train bearing with minimum sample［J］.Journal of Central South University（Science and Technology），2013，44（3）：963－969（in Chinese）

［16］Tyrone L Jones.Handbook of reliability prediction procedures for mechanical equipment（NSWC－11）［S］.USA Maryland：Naval Surface Warfare Center，2011

（编辑：李多）

Research of Reliability Assessment of Spacial Diaphragm Compressor

SHAO Limin YANG Haifeng ZHAO Xinpan
（Institute of Manned Spacecraft System Engineering，China Academy of Space Technology，Beijing 100094，China）

At present there is not an appropriate approach to making the reliability assessment of spacial diaphragm compressor.In this paper，based on the reliability evaluation of zero－failure data，a Bayesian reliability assessment applied in spacial diaphragm compressor is set up，which comprehensively utilizes partition distribution curve method，properties of failure rate functions for mechanical parts，and reliability prediction data.The feasibility of the proposed reliability assessment is verified by calculating examples.The calculating results show that the method could solve the problems of reliability evaluation with small sub－samples and zero－failure data for spacial diaphragm compressor，and provide the availability for the reliability assessment of similar kind of products.

spacial diaphragm compressor；small sub－sample；zero－failure sub－sample；reliability assessment

TH45

A

10.3969/j.issn.1673－8748.2016.05.015

2016－04－29；

2016－07－18

邵立民，男，高级工程师，主要研究方向为航天器总体设计和航天器系统可靠性设计与分析。Email：67934428@qq.com。