应用偏最小二乘法的卫星图像在轨几何检校方法

王恺 陈世平 曾湧

（1北京空间机电研究所，北京 100094）（2中国空间技术研究院，北京 100094）（3中国资源卫星应用中心，北京 100094）

应用偏最小二乘法的卫星图像在轨几何检校方法

王恺1陈世平2曾湧3

（1北京空间机电研究所，北京 100094）（2中国空间技术研究院，北京 100094）（3中国资源卫星应用中心，北京 100094）

高精度几何模型的建立及其参数的解算，是卫星图像在轨几何检校的核心工作。文章提出了一种应用偏最小二乘法的多参数误差方程整体解算方法，以解决基于误差几何模型的参数整体检校模型参数众多、参数间存在强相关性、参数估计复共线性等问题。以我国资源三号（ZY－3）卫星正视相机为例，对提出的方法进行验证。结果表明：文章提出的是一种精确、可靠的卫星图像在轨几何检校方法；在仅做一次几何检校时，ZY－3卫星正视相机相同数据平面定位精度优于3.10m，1年以后的平面定位精度优于15.00m。此方法可广泛应用于高分辨率光学卫星图像的在轨几何检校。

卫星图像；在轨几何检校；定位精度；偏最小二乘法

1 引言

遥感卫星图像分辨率已经进入亚米级时代，对图像质量的要求也从过去比较强调辐射质量发展到既要求高辐射质量又要求高几何质量。在轨几何检校的性能是决定卫星图像几何质量的关键因素之一。随着地面几何检校场等基础设施的日益完善，针对国内多颗光学卫星已系统地开展了在轨几何检校工作，大幅提升了我国光学卫星图像产品的几何质量。但是，在轨几何检校技术无论从理论研究还是应用实践上均相对滞后，有待进一步提高。

近几年，国内学者对高分辨率卫星图像在轨几何检校开展了大量研究工作。文献［1－3］中提出利用一个广义的偏移矩阵对相机进行几何外检校；文献［4－6］通过对姿态角常差建模求解，提高了几何定位精度；文献［7－11］中提出了一种基于探元指向角和相机安装角的几何检校模型，对相机进行几何检校；文献［12－14］中分析验证了国外星载线阵遥感器在轨几何检校模型。综上，卫星图像在轨几何检校方法主要分为两类：一类是基于误差几何模型的参数整体检校方法，即联合卫星图像的严格几何模型及误差几何模型，使用一定数量的地面控制点，通过自检校法进行系统几何误差的补偿；另一类是基于图像匹配的参数分步检校方法，即通过将参考图像与卫星图像进行相关对比，利用其差异反映原始模型的缺陷，进而改进模型，补偿图像几何误差。第一类采用一个包含众多附加参数的系统误差模型，相对第二类的模型更加严密，但是如果将附加参数作为自由未知参数参加平差，则会因过度参数化使解的精度恶化。因此，本文提出应用偏最小二乘法来求解误差方程，以解决参数估计的复共线性问题，可达到很好的效果。

针对高分辨率光学卫星图像，本文建立了基于误差几何模型的参数整体检校模型，推导了误差参数偏最小二乘估计公式，并以我国资源三号（ZY－3）卫星正视相机为研究对象，通过对其进行几何检校与定位精度评价试验，验证了本文在轨几何检校方法的有效性。

2 应用偏最小二乘法的几何检校方法

2.1 概述

构建合适的几何检校模型以及模型参数的解算，是实现高分辨率卫星图像在轨几何检校的核心。本文综合姿态、轨道等外方位元素模型、遥感器误差模型与严格几何成像模型，建立了几何检校模型。虽然对成像过程中各项系统误差均建立了精确的数学模型进行补偿，在理论上具有严密性，但是该模型中待检校参数众多，并且对于光学卫星图像而言，高轨道、窄视场角的几何成像特性，使得模型中各项参数之间具有高度相关性。已有的研究发现，利用一个包含许多附加参数的系统误差模型，在一定的几何条件下，特别是在较弱的几何条件下，会导致法方程式很坏的状态。如果将附加参数作为自由未知参数参加平差，则会因过度参数化而使解的精度恶化［15］。

一般，可采用逐步回归分析法、岭回归分析法等进行参数解算。但是，前者存在自变量取舍问题，且取舍的原则仅仅从该变量是否显著的数学原则出发，而未考虑其在系统中的具体意义和所起的作用，因此有些比较重要的自变量常被舍弃；在后者中，岭参数的确定非常困难，且随意性很大，其估计结果与岭参数选择密切相关，若选择不同的岭参数，得到的估计结果可能大不相同，不具有可推广性。本文采用偏最小二乘（Partial Least Squares，PLS）法，它集中了主成分分析、典型相关分析和多元线性回归分析的特点，有效克服了上述方法的缺点。

几何检校模型的偏最小二乘法解算流程，见图1。

图1 几何检校模型的偏最小二乘法解算流程Fig.1 Flow chart of solving geometric calibration model with PLS

偏最小二乘法最早由Herman Wold于20世纪60年代提出，后由S.Wold和Haetens首先将其应用于化工过程。该方法通过将自变量和因变量的高维数据空间投影到相应的低维特征空间，分别得到自变量和因变量的相互正交特征向量，建立自变量和因变量的特征向量间的一元线性回归关系，因此又被称为特征结构投影法［16］。

2.2 基于误差几何模型的几何检校模型构建

不同于文献［7］中内外检校参数分步解算的方法，本文将遥感器误差参数和定轨测姿系统误差参数共同纳入到自检校区域网平差的整体解算之中；在地面高精度控制信息的支持下，综合平衡内、外各项误差因素的影响，得到合理、稳定的几何检校参数。

1）外方位元素模型

外方位元素中的线元素模型为

式中：（XC（t），YC（t），ZC（t））为改正后的线元素；（XGPS（t），YGPS（t），ZGPS（t））为GPS设备给出的线元素；（Xoff，Yoff，Zoff）为待处理整景图像中线元素偏差的估计值，未知待求；t为卫星飞行时间。

外方位元素中的角元素模型为

式中：（φ（t），ω（t），κ（t））为改正后的角元素；（φm（t），ωm（t），κm（t））为测姿设备给出的角元素；（φ0，ω0，κ0）为角元素的偏差；（φ1，ω1，κ1）为角元素的漂移。2）遥感器误差模型遥感器误差模型为

式中：（Δx，Δy）为像点坐标的改正值；（xF，yF）为像点的焦平面坐标；（Δx0，Δy0）为CCD线阵在焦平面上的偏移参数；f为遥感器主距；Δf为遥感器主距系统误差参数；（k1，k1，k3）为光学系统径向畸变参数；（p1，p2）为光学系统偏心畸变参数；r为光学尺寸参数；θ为CCD旋转角度系统误差参数。

3）参数整体检校模型

综合外方位元素误差模型和遥感器误差模型，对严格几何模型进行改进整理得式（4）。其中，RCB为卫星本体坐标系到相机坐标系的转化矩阵，RBO为卫星本体坐标系到卫星轨道坐标系的转化矩阵，ROJ为卫星轨道坐标系到J2000坐标系的转化矩阵，RJW为J2000坐标系到WGS84坐标系的转化矩阵。卫星本体坐标系和卫星轨道坐标系的原点取卫星质心。［x y －f］为像点在相机坐标系中的坐标，［X Y Z］和［XSYSZS］分别为像点所对应的地面点和卫星质心在WGS84坐标系中的坐标，m′为比例系数。

在式（4）中引入遥感器误差扩展得

式中：

在卫星摄影测量中，通常将遥感器坐标系视为严格几何模型中的像空间坐标系，而物方坐标系可采用WGS84坐标系。定轨系统所测定的位置信息通常定义在WGS84坐标系下，而所测定的姿态通常定义为卫星本体坐标系相对轨道坐标系的旋转关系，显然不等同于摄影测量意义上的外方位角元素。为了进一步构建误差方程，要将姿态转换的系列矩阵引入扩展共线方程中，直接进行线性化处理，关键在于求出旋转矩阵R中每个元素对3个姿态角的一阶偏导数。R中诸元素不仅与卫星姿态有关，也会涉及相机、星敏感器的安装角，以及岁差、章动、极移等，进行线性化处理时会比较复杂，不过，R中的每个元素都是RCB，RBJ，RJW中元素的线性组合，而仅矩阵RBJ中的元素与姿态角有关，因此R中的诸元素对3个姿态角求一阶偏导数，关键在于RBJ中的元素对姿态角求导，而各元素是一些正弦、余弦三角函数的乘积，对其求导不再赘述。

在解算过程中，把附加参数处理成自由未知数一般是不合适的，因为其实际值总是很小，所以通常是把它处理成带权的观测值。如果将控制点也处理成带权观测值，将外方位元素误差公式（1）、（2）代入式（5）并线性化后，可建立误差方程式（8）。式（8）中某一行子式的通式可表示为〈Z，PW〉，其中，PW是子式Z中观测向量的权矩阵。

式中：位置偏差未知数增量向量Xo＝（ΔXoff，ΔYoff，ΔZoff）T；姿态偏差未知数增量向量Xs＝（Δφ0，Δω0，Δκ0）T；姿态漂移未知数增量向量Xd＝（Δφ1，Δω1，Δκ1）T；地面控制点坐标增量向量Xg＝（ΔX，ΔY，ΔZ）T；遥感器误差模型参数增量向量XΔ＝（Δx0′，Δf′，Δk1，Δk2，Δk3，Δp1，Δp2，Δθ）T，其中各项分别为参数Δx0，Δf，（k1，k1，k3），（p1，p2），θ的增量；A，Bs，Bd，C，D为相应的设计矩阵，C＝－A；V，L，P为相应的改正数向量、残差向量和权矩阵，V＝［VxVoVsVdVgVΔ］T，L＝［LxLoLs

LdLgLΔ］T，P＝diag（Px，Po，Ps，Pd，Pg，PΔ），V，L，P中各项是误差方程（8）中各式对应的改正数、残差和权矩阵，其中权矩阵采用验后权估计法确定。

2.3 几何检校模型参数的偏最小二乘法解算

设有p个自变量｛x1，x2，…，xp｝和q个因变量｛y1，y2，…，yq｝，为了研究自变量和因变量的统计关系，观测n个样本点，由此构成了自变量与因变量的数据表X＝（x1，x2，…，xp）n×p和Y＝（y1，y2，…，yq）n×q。用矩阵表示的偏最小二乘法回归模型为Yn×q＝Xn×pβ＋η （9）式中：β为回归系数；η为残差。

误差方程式（8）可以重新写为

V＝HG－L （10）

L＝HG－V （11）

与偏最小二乘法回归模型（式（9））对比，可见它们的形式是相似的。

设

式中：T＝［t1t2… tp］；P＝［p1p2… pp］；i＝1，2，…，p。

设

T＝［Hs1Hs2… Hsp］＝H［s1s2… sp］＝HS （13）

式中：S＝［s1s2… sp］；ti＝Hsi。

若分别将T，P，S分块，即T＝（T1T2），P＝（P1P2），S＝（S1S2），令PTG＝（P1P2）TG＝＝α，则

L＝HG－V＝TPTG－V＝（T1T2）（P1P2）TG－V＝T1P1TG＋T2P2TG－V＝T1α1＋T2α2－V （14）

只考虑取前m个成分时，得到新模型如下。

L＝T1α1－V＊（15）

式中：V＊为新的改正数向量。

可以算得新模型参数α1的最小二乘估计为

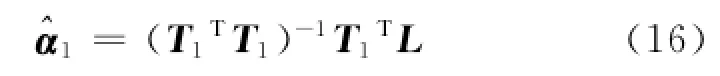
由于T1＝HS1，T2＝HS2，则

得到参数G在取m个成分的偏最小二乘估计结果为

3 定位精度评价

3.1 评价方案

以ZY－3卫星正视相机为例，对本文提出的几何检校方法进行验证。采用河南嵩山检校场和安阳地区的高质量数字正射图像（DOM）和数字高程模型（DEM），作为控制点提取及定位精度评价的参考数据；采用多幅参考图像区域的ZY－3卫星正视相机的一级图像，作为待评价数据。其中：嵩山区域参考数据平面精度优于1.50m，高程精度优于2.00m；安阳区域参数数据平面精度优于2.50m，高程精度优于16.00m。首先，使用嵩山区域不同时间图像采用本文方法作几何检校，并在同数据上作质量评价；然后，使用2012年11月19日图像进行几何检校后获取的模型，对嵩山区域及安阳区域不同时间图像分别进行评价。

3.2 评价结果与分析

根据上文中的方案，对嵩山区域和安阳区域图像进行直接定位精度评价，结果见表1～4。

表1 无检校直接定位精度（嵩山地区）Table 1 Positioning accuracy without calibration（Songshan）

表2 相同数据定位精度（嵩山地区）Table 2 Positioning accuracy of the same data（Songshan）

表3 相同地区、不同时间的数据定位精度（嵩山地区）Table 3 Positioning accuracy of data at the different time in the same area（Songshan）

表4 不同时间、不同地区的数据定位精度（安阳地区）Table 4 Positioning accuracy of data at the different time in the different area（Anyang）

表1给出了嵩山区域2012年11月19日图像未检校直接定位精度。表2给出了在嵩山区域各景图像上进行检校后，再在同图像上进行评价的结果。表3给出了使用2012年11月19日图像上检校出的模型，分别对嵩山区域的其他卫星图像进行定位精度评价的结果。表4给出了使用2012年11月19日图像上检校出的模型，分别对安阳区域的卫星图像进行定位精度评价的结果。各表中精度均为UTM投影坐标系下的结果，横坐标轴（X轴）方向为东西方向，向东为正，纵坐标轴（Y轴）方向为南北方向，向北为正；和分别表示检查点残差在X轴方向和Y轴方向的平均误差；表示检查点残差向量幅值的平均误差；和分别表示检查点残差在X轴方向和Y轴方向的中误差；表示检查点的平面精度。

表1中数据表明，未经几何检校的ZY－3卫星正视相机原始图像直接定位精度较差，且X轴方向精度与Y轴方向精度相差较大，必须开展在轨几何检校。

从表2可知，经过几何检校，ZY－3卫星正视相机图像定位精度有了大幅提高，就2012年11月19日的图像而言，平面精度从1 017.30m提高到2.14m。经过检校的模型已经很好地补偿了系统误差。表2中的数据是对在轨几何检校时采用的同图像进行精度评价的结果（先使用一幅图像进行几何校正模型解算，再使用得出的模型在这幅图像上进行评价），因此也反映了图像的内部几何质量。从表2中可见，平面精度优于3.10m，即优于1.5个像元。

在表3和表4中，成像时间间隔较长、地理位置不同，反映出定位精度在一次几何检校后的变化情况。可以看出，随着成像时间推移，直接定位精度逐渐变差，且在数值上表现出明显的系统性，即Y轴方向的精度明显优于X轴方向的精度。一般而言，定位精度主要取决于外定向精度。在相同幅度的误差条件下，角元素的影响远大于线元素。ZY－3卫星轨道测量精度优于米级，因此以上系统误差主要来自角元素误差，即姿态漂移、遥感器安装角误差和时间同步误差。综合分析表3和表4中的平面定位精度，可以看出：从2012年11月19日几何检校开始，1年以后的平面精度优于15.00m。这不仅说明ZY－3卫星自发射以来，平台和有效载荷运行状态良好，而且充分说明本文提出的在轨几何检校方法有效、可靠。

4 结束语

本文提出了一种应用偏最小二乘法的多参数误差方程整体解算方法，对于基于误差几何模型的参数整体检校模型参数众多、参数间存在强相关性、参数估计的复共线性问题，提供了一种解决方法。对ZY－3卫星正视相机进行几何检校与定位精度评价试验，验证了本文在轨几何检校方法的有效、可靠，且精度较高。不过，受条件限制，本文采用的试验数据有限，无法获取更高精度的参考数据，试验结果难免存在不足。本文引入偏最小二乘法克服参数估计多重共线性的问题，得了一定的效果，但是对偏最小二乘法中成分选择的准则，还须结合几何检校的需求开展进一步研究。

（

）

［1］徐建艳，侯明辉，于晋，等.利用偏移矩阵提高CBERS图像预处理几何定位精度的方法研究［J］.航天返回与遥感，2004，25（4）：25－29 Xu Jianyan，Hou Minghui，Yu Jin，et al.Study of CBERS CCD camera bias matrix calculation and its application［J］.Spacecraft Recovery ＆Remote Sensing，2004，25（4）：25－29（in Chinese）

［2］张过.缺少控制点的高分辨率卫星遥感影像几何纠正［D］.武汉：武汉大学，2005 Zhang Guo.Rectification for high resolution remote sensing image under lack of ground control points［D］.Wuhan：Wuhan University，2005（in Chinese）

［3］祝小勇，张过，唐新明，等.资源一号02B卫星影像几何外检校研究及应用［J］.地理与地理信息科学，2009，25（3）：16－18 Zhu Xiaoyong，Zhang Guo，Tang Xinming，et al.Research and application of CBRS02Bimage geometric exterior calibration［J］.Geography and Geo－Information Science，2009，25（3）：16－18（in Chinese）

［4］袁修孝，余俊鹏.高分辨率卫星遥感影像的姿态角常差检校［J］.测绘学报，2008，37（1）：36－41 Yuan Xiuxiao，Yu Junpeng.Calibration of constant angular error for high resolution remotely sensed imagery［J］.Acta Geodaetica et Cartographica Sinica，2008，37（1）：36－41（in Chinese）

［5］余俊鹏.高分辨率卫星遥感影像的精确几何定位［D］.武汉：武汉大学，2009 Yu Junpeng.Accurate geometric positioning of high resolution satellite remote sensing imagery［D］.Wuhan：Wuhan University，2009（in Chinese）

［6］袁修孝，余翔.高分辨率卫星遥感影像姿态角系统误差检校［J］.测绘学报，2012，41（3）：385－392 Yuan Xiuxiao，Yu Xiang.Calibration of angular systematic errors for high resolution satellite imagery［J］.Acta Geodaetica et Cartographica Sinica，2012，41（3）：385－392（in Chinese）

［7］李德仁，王密.“资源三号”卫星在轨几何定标及精度评估［J］.航天返回与遥感，2012，33（3）：1－6 Li Deren，Wang Mi.On－orbit geometric calibration and accuracy assessment of ZY－3［J］.Spacecraft Recovery ＆Remote Sensing，2012，33（3）：1－6（in Chinese）

［8］杨博，王密.资源一号02C卫星全色相机在轨几何定标方法［J］.遥感学报，2013，17（5）：1175－1190 Yang Bo，Wang Mi.On－orbit geometric calibration method of ZY－1 02Cpanchromatic camera［J］.Journal of Remote Sensing，2013，17（5）：1175－1190（in Chinese）

［9］Wang Mi，Yang Bo，Hu Fen，et al.On－orbit geometric calibration model and its applications for high－resolution optical satellite imagery［J］.Remote Sensing，2014，6（5）：4391－4408

［10］徐文，龙小祥，喻文勇，等.“资源三号”卫星三线阵影像几何质量分析［J］.航天返回与遥感，2012，33（3）：55－64 Xu Wen，Long Xiaoxiang，Yu Wenyong，et al.Geometric quality analysis of three－line array CCD imagery of ZY－3satellite［J］.Spacecraft Recovery ＆Remote Sensing，2012，33（3）：55－64（in Chinese）

［11］蒋永华，张过，唐新明，等.资源三号测绘卫星三线阵影像高精度几何检校［J］.测绘学报，2013，42（4）：523－529 Jiang Yonghua，Zhang Guo，Tang Xinming，et al.High accuracy geometric calibration of ZY－3three－line image［J］.Acta Geodaetica et Cartographica Sinica，2013，42（4）：523－529（in Chinese）

［12］苏文博.航天线阵CCD传感器在轨几何检校技术研究［D］.郑州：信息工程大学，2010 Su Wenbo.Research on techniques for on－orbit geometric calibration of space linear CCD sensors［D］.Zhengzhou：PLA Information Engineering University，2010（in Chinese）

［13］雷蓉.星载线阵传感器在轨几何检校的理论和算法研究［D］.郑州：信息工程大学，2011 Lei Rong.Study on theory and algorithm of the in－flight geometric calibration of spaceborne linear array sensor［D］.Zhengzhou：PLA Information Engineering University，2011（in Chinese）

［14］刘楚斌.高分辨率遥感卫星在轨几何定标关键技术研究［D］.郑州：信息工程大学，2012 Liu Chubin.Study on crucial technique of the on－orbit geometric calibration of high resolution satellite［D］.Zhengzhou：PLA Information Engineering University，2012（in Chinese）

［15］李德仁，袁修孝.误差处理与可靠性理论［M］.武汉：武汉大学出版社，2012 Li Deren，Yuan Xiuxiao.Error processing and reliability theory［M］.Wuhan：Wuhan University Press，2012（in Chinese）

［16］王桂增，叶昊.主元分析与偏最小二乘法［M］.北京：清华大学出版社，2012 Wang Guizeng，Ye Hao.Principal component analysis and partial least squares method［M］.Beijing：Tsinghua University Press，2012（in Chinese）

（编辑：夏光）

On－orbit Geometric Calibration Method of Satellite Imagery Based on Partial Least Squares Method

WANG Kai1CHEN Shiping2ZENG Yong3
（1Beijing Institute of Space Mechanics ＆Electricity，Beijing 100094，China）
（2China Academy of Space Technology，Beijing 100094，China）
（3China Center for Resources Satellite Data and Application，Beijing 100094，China）

Building the high precision geometric model and calculating the model parameters are the core work of the satellite imagery on－orbit geometric calibration.This paper presents a new overall solution of the error equation with multi parameters based on partial least squares method，in order to solve some problems about the overall parameter calibration model based on geometric error model，including many parameters in the model，strong correlation between the parameters，and multicollinearity of parameter estimation.The method proposed is validated with ZY－3satellite nadir camera，and the results show that it is an accurate and reliable on－orbit geometric calibration method for satellite image.With one geometric calibration，the plane positioning accuracy is better than 3.10m，and better than 15.00mafter one year.The method can be widely applied to on－orbit geometric calibration of the high resolution optical satellite imagery.

satellite imagery；on－orbit geometric calibration；positioning accuracy；partial least squares method

P236

A

10.3969/j.issn.1673－8748.2016.05.005

2016－06－22；

2016－08－17

国家重大航天工程

王恺，男，工程师，研究方向为航天摄影测量与遥感。Email：wmsxd@sohu.com。