敏捷卫星主动推扫成像积分时间设置研究

余婧 于龙江 李少辉 王跃 张国斌 杨文涛

（北京空间飞行器总体设计部，北京 100094）

敏捷卫星主动推扫成像积分时间设置研究

余婧 于龙江 李少辉 王跃 张国斌 杨文涛

（北京空间飞行器总体设计部，北京 100094）

针对敏捷卫星的新型工作方式——主动推扫成像过程中的积分时间设置开展了研究。通过建立敏捷卫星主动推扫成像典型场景和积分时间模型，仿真了敏捷卫星主动推扫成像过程中相机TDICCD的积分时间变化情况，并给出了设置建议。文章对两种典型工况进行了仿真计算，均为卫星对垂轨条带进行扫描，条带长度分别为170km和1520km，仿真结果表明：积分时间在主动推扫成像过程中实时变化，同时在大角度机动下，边缘和中心视场的积分时间有较大差异。积分时间的实时变化需要进行积分时间的实时设置，并仿真给出了设置频率的需求；而积分时间边缘和中心视场的不一致，需要进行积分时间的分片设置。分析表明采用这些措施后，主动推扫过程中由于积分时间设置引起的图像MTF下降能得到有效控制。文章的仿真结果可以为我国敏捷卫星总体的设计和相机的设计提供参考。

敏捷卫星；主动推扫成像；积分时间；设置

1 引言

敏捷卫星已成为当今遥感卫星的重要发展方向。敏捷卫星能够在短时间内实现大角度快速机动，利用其快速姿态机动能力，迅速改变星上相机对地指向，实现对地面目标的高效、灵活的观测。世界不少国家已成功发射或正在研究敏捷卫星。比较典型的有美国的艾科诺斯（Ikonos）系列［1］、世界观测卫星（Worldview）系列［2－3］，法国的昴宿星（Pleiades）［45］系列等，国内目前也正在开展相关研究工作。此类卫星在成像工作模式上进行了扩展［6－7］，除了常规的被动推扫成像外，还增加了主动推扫成像方式。利用主动推扫成像方式可以获得用户定制的非沿迹条带的目标图像。这种成像方式的出现，一方面大大提高了成像灵活性和成像效率，但另一方面又对卫星成像质量的保证提出了新的难题［8－9］，如何保证这种成像方式下的成像质量成为亟待解决的问题。

国内低轨遥感卫星相机一般采用TDICCD成像，卫星成像过程中姿态保持固定，依靠被动地速进行推扫成像，积分时间基本保持恒定［10］，即传统的被动推扫成像方式。主动推扫成像过程中，卫星进行“动中成像”，卫星姿态在成像过程中实时变化，观测斜距、像面扫描速度实时变化，导致积分时间在成像过程中实时变化。当卫星观测机动角度较大时，焦面中心视场和边缘视场积分时间之间的差异较大。这些都会降低卫星图像调制传递函数（MTF），导致图像质量的下降。

本文首先建立了敏捷卫星主动推扫成像过程和积分时间计算模型，并针对两种典型主动推扫成像工况，仿真计算了这两工况下卫星积分时间。仿真结果体现了积分时间在主动推扫成像过程中实时变化情况及大角度机动下边缘和中心视场下积分时间差异情况。随后分析了采用传统积分时间设置方式下，积分时间的设置误差对卫星图像MTF的影响。最后给出了主动推扫成像过程对积分时间设置的要求。

积分时间的实时变化需要进行积分时间的实时设置；而边缘和中心视场积分时间的不一致则需要进行积分时间的分片设置补偿。分析表明采用这些措施后，主动推扫过程中由于积分时间设置引起的图像MTF下降能得到有效控制。

2 主动推扫成像过程和积分时间计算模型

主动推扫成像过程中卫星姿态持续机动，各个主动推扫过程之间也存在卫星姿态的转换。本文中暂时只考虑卫星单个主动推扫成像过程，图1给出单个主动推扫成像过程一般场景。

图1 主动推扫成像模型Fig.1 Active imaging process model

图1中MS点为卫星开始执行本段任务时对应的星下点；ME为卫星结束执行本段任务时对应的星下点；B1s为开始成像时，卫星对应的星下点；C1s为结束成像时，卫星对应的星下点；B1s－C1s为卫星的成像过程；B1为开始成像时的摄影点，此时卫星姿态机动速度满足合成推扫速度要求，且角速度稳定度满足成像要求；C1为相机结束成像时的摄影点。图1中虚线为摄影点在地表的移动过程。

主动推扫成像模式下，卫星可以对用户指定的任意地面条带（可以平行于星下点轨迹，也可以不平行于星下点轨迹）进行成像。用户（或任务规划系统）指定地面条带的起点、终点位置，并用一条直线将起点、终点连接（严格讲是大圆上的一段弧线）。主动推扫成像过程中，令摄影点在该直线上沿某种方式运动（本文的仿真计算主要考虑匀地速主动推扫成像模式，即摄影点的移动为均匀地速方式），进而得到星体滚动角、俯仰角的变化曲线（即规划曲线）。该模式下，滚动/俯仰角度变化过程一般为非线性，滚动/俯仰角速度变化过程一般也是非线性的。成像过程中，为了保证成像质量，要保证卫星姿态角速度稳定度和姿态指向精度满足成像要求。同时在成像过程中，卫星需绕偏航轴实时机动进行偏航角修正，以使相机焦面上的像移方向垂直于相机TDICCD的线阵方向。

积分时间T为相机像元尺寸d与相机焦面像速沿飞行方向分量vx的比值。

主动推扫情况下地面目标点相对相机的速度公式如下，与传统卫星相比还需要考虑卫星姿态角速度的影响。

v＝ωe×R－［ωn×r＋（ωn＋ωs）×H＋vr］＝ωe×R－ωn×R－ωs×H－vr（2）

将式（2）中的v投影到相机本体坐标系中，得到相对速度在相机本体坐标系中的矢量形式，求得成像平面上的两个速度分量vx和vy，进而求得积分时间T。

其中ωs表示卫星的姿态角速度；ωe是地球角速度矢量；R是地心到目标点的矢量；vr是卫星绝对速度的径向分量；H是卫星到目标点的距离矢量；r是地心指向卫星的矢径，其大小为r；ωn是轨道角速度矢量。

3 主动推扫成像过程典型场景仿真

建立主动推扫典型场景，仿真计算主动推扫成像过程中的姿态和积分时间的变化情况。典型场景的选取考虑采用比较极端的主动推扫成像过程，即观测条带与卫星的星下点轨迹之间相互垂直。这种工况更能体现主动推扫成像模式和传统被动推扫成像模式之间的区别。传统卫星只能对与星下点轨迹平行的观测条带成像。在观测条带与星下点轨迹垂直这种成像场景下，卫星的偏流角需要调整较大的角度来保证焦面像移方向与TDICDD线阵的垂直。选取两种条带长度，分别为170km和1520km。条带170km场景用来分析卫星俯仰角和滚动角较小的情况，而条带1520km场景用来分析卫星俯仰角和滚动角较大的情况。假设卫星轨道高度为650km太阳同步轨道，成像地速采用7km/s均匀地速。仿真采用MATLAB软件程序编程实现。

3.1 主动推扫典型场景建立

1）工况ZD－170

观测条带垂直于星下点轨迹，条带起点经纬度（－14°，＋46.4°）；终点经纬度（－12°，＋45.8°）；条带长度170km；起始时刻点5088s；结束时刻点5112s。（假设轨道初始时刻为2015年7月1日 12：00：00：000UTCG）

典型成像场景如图2所示，图2（a）中红色线表示卫星的星下点轨迹，蓝色线为卫星的摄影点轨迹，即遥感相机的扫描条带。卫星成像过程中滚动角、俯仰角和偏航角实时变化如图2（b）所示。这种工况下，卫星的俯仰角和滚动角变化在±10°以内，偏航角调整较大，达－80°。

图2 ZD－170主动推扫成像过程典型成像场景和卫星姿态角变化Fig.2 Typical active imaging scene and satellite attitude variation－case ZD－170

2）工况ZD－1520

观测条带垂直于星下点轨迹，条带起点经纬度（－21°，＋50°）；终点经纬度（－5°，＋42°）；条带长度1520km；起始时刻点4995s；结束时刻点5210s。

典型成像场景如图3所示，图3（a）给出了卫星的星下点轨迹和扫描条带；图3（b）给出了卫星成像过程中姿态角的变化。这种工况下，卫星的俯仰角和滚动角变化较大，尤其是滚动角，接近±50°，同样偏航角也较大。

图3 工况ZD－1520主动推扫成像过程典型成像场景和卫星姿态角变化Fig.3 Typical active imaging scene and satellite attitude variation－case ZD－1520

3.2 主动推扫典型场景下的积分时间变化及其影响

3.2.1 积分时间的实时变化情况

仿真给出工况ZD－170和工况ZD－1520下的积分时间变化（归一化后）如图4所示。

从仿真结果可见，主动推扫成像过程中，卫星积分时间实时变化。如果沿用传统遥感卫星某一条带成像过程中积分时间保持恒定的设置方法，会导致卫星图像质量的下降。下面使用图像MTF值来衡量积分时间对图像质量造成的影响。MTF就是图像调制度与目标调制度之比的函数，是表征成像系统空间分辨能力的主要指标。MTF是表征成像系统质量的重要参数，是目前用户用于评价图像质量的重要像质要素之一。

假设由于积分时间误差导致的像移为Δd，则对图像MTF影响为：sinc（π×fN×Δd）。其中，fN为奈奎斯特频率（fN＝1/2d）；d为焦面的像元尺寸。假设应该设置的积分时间为T0，而实际设置的积分时间为T1，N为TDICCD积分级数。则有

下面计算如果积分时间在推扫过程中保持恒定，对主动推扫成像产生的影响。假设两个工况下的整个主动推扫成像过程的积分时间均取为1，积分时间级数设置取48。工况ZD－170，主动推扫始端的积分时间设置应为1.028 0，若积分时间取为1，则始端图像MTF下降为0.406 2。而工况ZD－1520，主动推扫终端的积分时间接近2，即整个主动推扫成像过程中图像的积分时间变化接近1倍。若积分时间统一取为1，则扫描始端和终端图像的MTF下降为0。图像将完全不可用。

图4 主动推扫成像过程典型成像场景积分时间变化Fig.4 Variation of TDICCD integral time during typical active imaging process

3.2.2 不同视场的积分时间

卫星在大角度机动情况下，相机边缘和中心视场积分时间存在差异，这时如果按照相机中心视场进行整个焦面的积分时间设置，将造成焦面边缘视场图像MTF值的下降。不同机动角度下相机焦面中心和边缘视场的积分时间计算如图5所示。

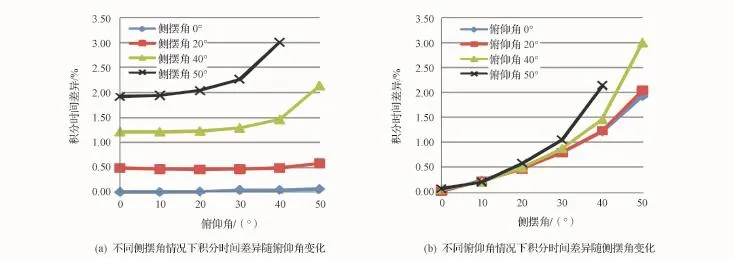
图5 典型工况下相机焦面边缘与中心视场积分时间差异Fig.5 Difference of integral time between edge and center position of TDICCD in typical active imaging process

由图5可见卫星机动角度越大，相机中心视场和边缘视场之间积分时间的差异越大，且随着侧摆角增大对该效应的影响远远大于俯仰角的增加。这也是可以理解的，因为侧摆角增大，中心视场和边缘视场像元的对地斜距差异远远大于俯仰角增大的情况。当卫星俯仰角和滚动角都为30°时（取TDI级数为48），如果全焦面均采用中心视场积分时间进行设置，则边缘视场积分时间设置误差为0.81%，对图像边缘视场图像MTF的影响为下降到0.939 0；当卫星俯仰和滚动角都为45°时（取TDI级数为48），边缘视场积分时间设置误差为2.4%，对图像边缘视场图像MTF的影响为下降到0.536 9。在采用积分时间全焦面统一设置的情况下，机动角度越大，图像边缘视场图像MTF下降越大。

4 主动推扫成像过程对积分时间设置要求

从上述仿真计算的主动推扫成像过程中，敏捷卫星积分时间实时变化，且在机动角度较大的情况下，相机焦面边缘和中心视场积分时间存在较大差异。如果仍按照传统的积分时间设置方式，卫星图像MTF将由于主动推扫成像方式下降很大，造成图像质量的降低，甚至图像不可用。因此需要探索主动推扫成像方式下的新型积分时间设置方法。这里针对积分时间的实时变化提出积分时间的实时设置；针对积分时间的不同视场的差异提出积分时间的分片设置，并仿真分析采取这些积分时间设置方法后，卫星图像质量的提升。

4.1 积分时间实时变化对设置的要求

主动推扫成像过程中积分时间的实时变化要求积分时间的实时设置，而实时设置的频率对图像质量提升效果有较大的影响。下面研究积分时间的设置频率对图像质量的影响。

如果要求积分时间实时变化导致的图像MTF下降优于0.990 0，则要求积分时间设置频率原因导致的像移要控制在0.02个像元以内，此时图像MTF的下降为0.998 4。这就要求：

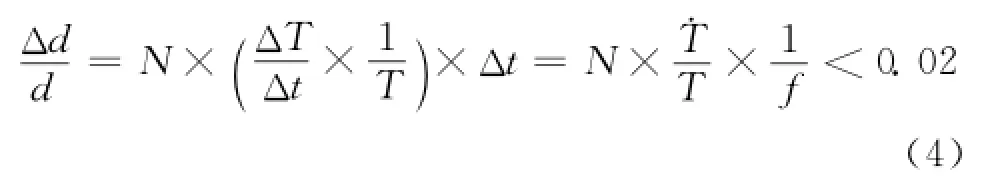
式中：f为积分时间设置频率。定义（T/T）为“积分时间相对变化率”，为积分时间的变化速率与当前积分时间之比。通过定义积分时间相对变化率，可以方便分析积分时间设置频率对卫星图像MTF的影响。

工况ZD－170和工况ZD－1520下的积分时间相对变化率如图6所示。

工况ZD－170下，积分时间变化率T/T不超过4×10－3，当积分级数N取48时，则要求卫星积分时间的设置频率f大于10Hz，即积分时间设置频率大于10Hz，可以保证积分时间实时变化导致的像移在0.02个像元以内。当积分级数取24和92时，要求积分时间的设置频率f分别大于5Hz和19Hz。

工况ZD－1520下，积分时间变化率T/T不超过8×10－3，当积分级数取48时，则要求卫星积分时间的设置频率f大于20Hz，即积分时间设置频率大于20Hz，可以保证优于积分时间实时变化导致的像移在0.02个像元以内。当积分级数取24和92时，要求积分时间的设置频率f分别大于10Hz和40Hz。

图6 主动推扫成像过程典型成像场景积分时间相对变化率Fig.6 Relative variation of TDICCD integral time during typical active imaging process

4.2 积分时间中心和边缘差异对设置的要求

中心视场和边缘视场积分时间的不一致可以通过卫星的分片积分时间设置的方法来解决。假设卫星相机焦面由3片CCD拼接而成，各片CCD分别按照各自中心点积分时间进行设置，下面给出采用这种分片设置方法后对图像MTF的改进。

焦面中心相机CCD片的图像MTF值变化仿真计算结果如图7所示。

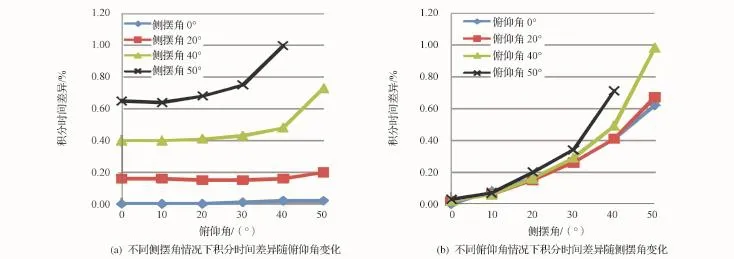
图7 采用分片积分时间设置后焦面中心CCD片边缘与中心视场积分时间差异Fig.7 Difference of integral time between edge and center position of center CCD in typical active imaging process

焦面边缘相机CCD片的图像MTF值变化分析如图8所示。

可见采取分片积分方法后，能有效提升图像的MTF指标，当卫星俯仰和滚动角都为30°时（取TDI级数为48），焦面中心和边缘CCD片的中心和边缘视场积分时间设置误差优于0.26%，明显优于采用积分时间分片计算前的0.81%，此时图像MTF下降为0.993 6；当卫星俯仰角和滚动角都为45°时（取TDI级数为48），焦面中心和边缘CCD片的中心和边缘视场积分时间设置误差优于0.82%，明显优于采用积分时间分片计算前的2.4%，此时图像MTF下降为0.937 5。可见采取积分时间分片设置后，对图像MTF有很大改善，在卫星机动角度越大时越明显。

图8 采用分片积分时间设置后焦面中心CCD片边缘与中心视场积分时间差异Fig.8 Difference of integral time between edge and center position of edge CCD in typical active imaging process

5 结论

仿真表明积分时间在主动推扫成像过程中实时发生变化，同时在大角度机动下，边缘和中心视场的积分时间有较大差异。这些都会造成卫星图像质量的下降。针对这一问题本文提出了积分时间实时设置和分片设置的解决措施，仿真计算表明采用这些措施后，主动推扫过程中的由于积分时间设置引起的图像MTF下降能得到有效控制，显著提升了图像质量。本文的工作可以为我国敏捷卫星的总体设计提供参考。

（

）

［1］Dial G，Bowen H，Gerlach F，et al.IKONOS satellite，imagery，and products［J］.Remote Sensing of Environment，2003，88（1），23－36

［2］Jawak S D，Luis A J.Application of Worldview－2satellite data for extraction of polar spatial information and DEM of Larsemann Hills，East Antarctica［J］.Remote Sensing and Environment Letters，2012，2（1）：19

［3］Jawak S D，Luis A J，Panditrao S N，et al.Advancement in landcover classification using very highresolution remotely sensed 8－band WorldView－2satellite data［J］.International Journal of Earth Science and Engineering，2013，6（2）：1742－1749

［4］Astrium Company.Pleiades imagery user guide［Z］.Cedex：Astrium Company，2012

［5］M Alain Gleyzes，Lionel Perret，Philippe Kubik.Pleiades system architecture and main performances［J］.International Archives of the Photogrammetry，Remote Sensing and Spatial Information Sciences，2012，XXXIX－B1：537－542

［6］余婧，喜进军，于龙江，等.敏捷卫星同轨多条带拼幅成像模式研究［J］.航天器工程，2015，24（2）：27－34 Yu Jing，Xi Jinjun，Yu Longjiang，er al.Study of one－orbit multi—stripes splicing imaging for agile satellite［J］.Spacecraft Engineering，2015，24（2）：27－34（in Chinese）

［7］张新伟，戴君，刘付强.敏捷遥感卫星工作模式研究［J］.航天器工程，2011，20（4）：32－38 Zhang Xinwei，Dai Jun，Liu Fuqiang.Research on working mode of remote sensing satellite with agile attitude control［J］.Spacecraft Engineering，2011，20（4）：32－38（in Chinese）

［8］黄群东，杨芳，赵键.敏捷成像时TDICCD积分时间调整及基于MTF的像移分析［C］//2011年小卫星技术交流会.北京：航天东方红卫星有限公司，2011 Huang Qundong，Yang Fang，Zhao Jiang.The integral time adjusting of the TDICCD and the image motion analysis based on MTF for the agile imaging［C］//2011 Small Satellite Technique Symposium.Beijing：DFH Co.Ltd.，2011（in Chinese）

［9］黄群东，杨芳，赵键.姿态对地指向不断变化成像时的像移速度计算［J］.光学精密工程，2012，20（12）：2812－2820 Huang Qundong，Yang Fang，Zhao Jiang.Calculation of image motion velocity for agile satellite dynamic imaging to changed continuously attitude point［J］.Optics and Precision Engineering，2012，20（12）：2812－2820（in Chinese）

［10］樊超，李英才，易红伟.速高比对TDICCD相机的影响分析［J］.兵工学报，2007，28（7）：817－821 Fan Chao，Li Yingcai，Yi Hongwei.Influence of velocityheight ratio of satellite on the TDICCD camera［J］.Acta Armamentarii，2007，28（7）：817－821（in Chinese）

（编辑：张小琳）

Study of Integral Time of TDICCD During Active Imaging of Agile Satellite

YU Jing YU Longjiang LI Shaohui WANG Yue ZHANG Guobin YANG Wentao
（Beijing Institute of Spacecraft System Engineering，Beijing 100094，China）

This article studies a new working mode（active imaging mode）of agile satellite.An active imaging process model and an integral time of the TDICCD calculation model are built，and the integral time of the TDICCD during active imaging process is simulated.The setting demand of the integral time is given according to the calculation results.Two typical cases are simulated and calculated.These both cases are with the imaging strip perpendicular to the sub－track，except the different length of the imaging strip.One is 170km，and the other is 1520km.The simulation and calculation results indicate that the integral time is changing all along the active imaging process，and in the large－angle imaging situation，the integral time at the edge and the center of the TDICCD have great difference.The real－time changing of the integral time needs the real－time setting of the integral time during the active imaging process and the difference of the integral time at different position of the TDICCD needs setting the integral time of different CCD separately.Analysis shows that with these setting being made，the descent of MTF of the imaging picture due to active imaging can be efficiently controlled.The calculation results of this article can give advice to the design of agile satellite and its camera.

agile satellite；active imaging；integral time；setting

TP79

A

10.3969/j.issn.1673－8748.2016.05.004

2016－05－31；

2016－08－25

国家重大航天工程

余婧，女，工程师，从事航天器总体设计和载荷类研究工作。Email：yuj421@gmail.cn。