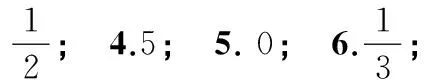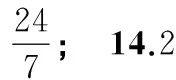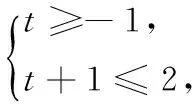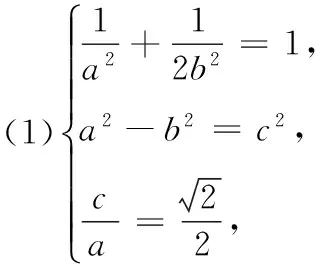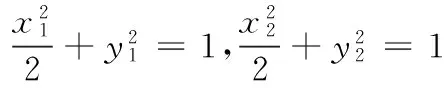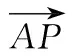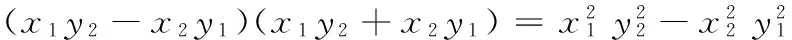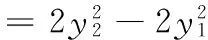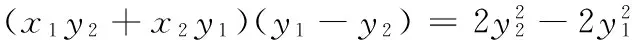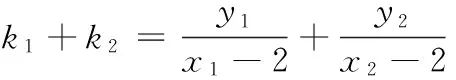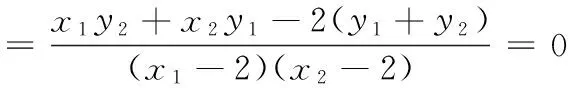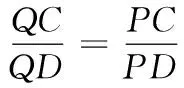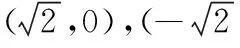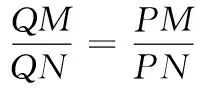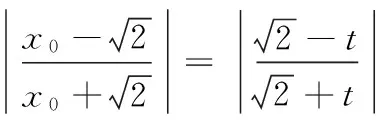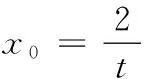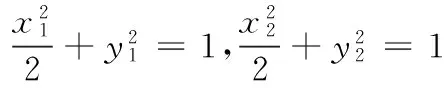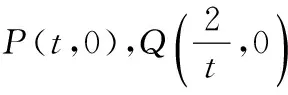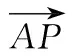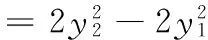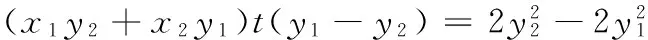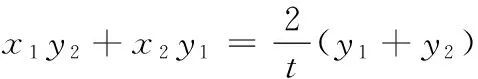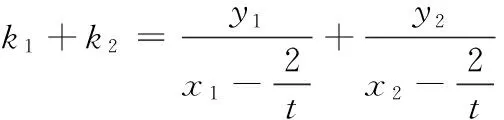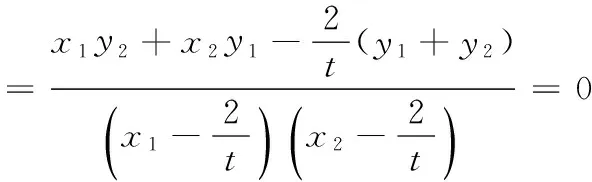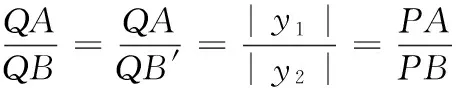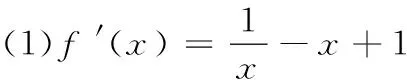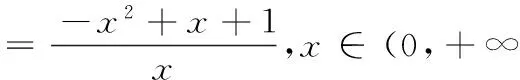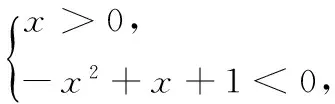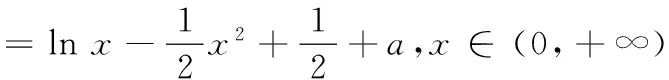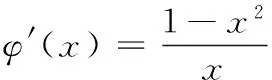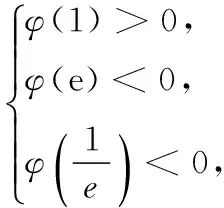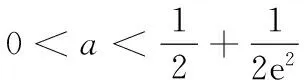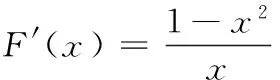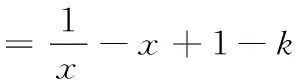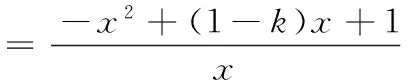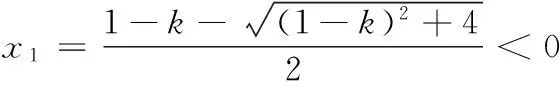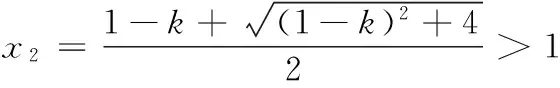高二数学测试
2016-12-01
高二数学测试
一、填空题(本大题共14小题,每小题5分,共70分)
1.命题“∀x∈R,x2+x+1>0”的否定是______.
2.某工厂生产A、B、C三种不同型号的产品,产品数量之比为2∶3∶5,现用分层抽样的方法抽取容量为n的样本,样本中A型号产品有15件,那么样本容量n为______.
3.在区间[0,4]上任取一个实数x,则x>2的概率是______.
4.根据如图所示的伪代码,如果输入x的值为0,则输出结果y为______.
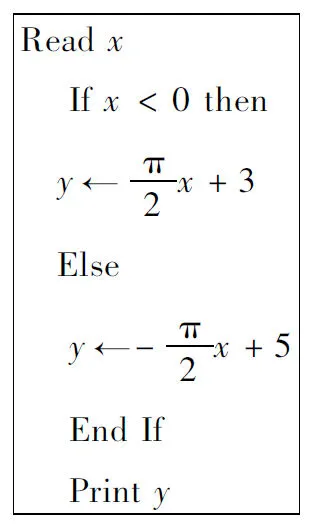
第4题图
6.在三张奖券中有一、二等奖各一张,另一张无奖,甲乙两人各抽取一张(不放回),两人都中奖的概率为______.
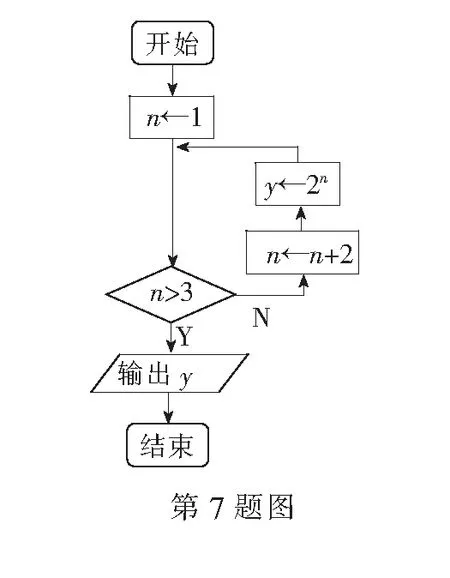
7.如图,该程序运行后输出的y值为______.
8.一个圆锥筒的底面半径为3 cm,其母线长为5 cm,则这个圆锥筒的体积为______cm3.
10.设l,m是两条不同的直线,α,β是两个不重合的平面,给出下列四个命题:
① 若α∥β,l⊥α,则l⊥β;
② 若l∥m,l⊂α,m⊂β,则α∥β;
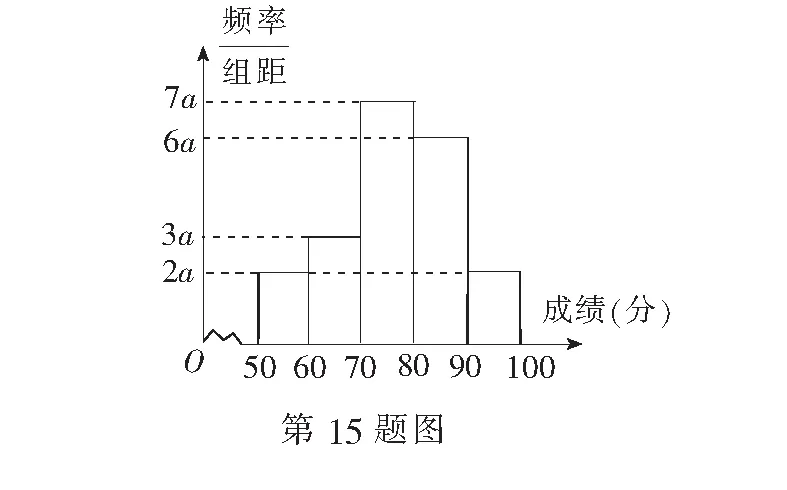
③ 若m⊥α,l⊥m,则l∥α;
④ 若l∥α,l⊥β,则α⊥β.
其中真命题的序号有______.(写出所有正确命题的序号)
12.已知可导函数f(x)(x∈R)的导函数f ′(x)满足f(x) 13.若椭圆的中心为坐标原点,长轴长为4,一条准线方程为x=-4,则该椭圆被直线 y=x+1截得的弦长为______. 14.若a>0,b>0,且函数f(x)=aex+(b2-3)x在x=0处取得极值,则ab的最大值等于______. 15.(本小题满分14分)某班40名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.(学生成绩都在[50,100]之间) (1)求频率分布直方图中a的值; (2)估算该班级的平均分; (3)若规定成绩达到80分及以上为优秀等级,从该班级40名学生中任选一人,求此人成绩为优秀等级的概率. 16.(本小题满分14分)如图,在四面体ABCD中,AB⊥CD,AB⊥AD,M,N,Q分别为棱AD,BD,AC的中点. (1)求证:CD∥平面MNQ; (2)求证:平面MNQ⊥平面ACD. (1)若“p且q”是真命题,求m的取值范围; (2)若q是r的必要不充分条件,求t的取值范围. 18.(本小题满分15分)已知函数f(x)=-x3+3x2+9x+a. (1)当a=-2时,求f(x)在x=2处的切线方程; (2)若f(x)在区间[-2,2]上的最大值为22,求它在该区间上的最小值. (1)求椭圆E的方程; (2)若椭圆E的右焦点是P,其右准线与x轴交于点Q,直线AQ的斜率为k1,直线BQ的斜率为k2,求证:k1+k2=0; (1)求函数f(x)的单调递减区间; (3)若存在x0>1,当x∈(1,x0)时,恒有f(x)>kg(x),求实数k的取值范围. 一、填空题 1.∃x∈R,x2+x+1≤0; 2.75; 7. 32; 8.12π; 9.7; 10.① ④; 11.y=±x; 12.[2 016,+∞); 二、解答题 15.(1)由题意得 (2a+2a+3a+6a+7a)×10=1, ∴20a×10=1, ∴a=0.005. 16.(1)因为M,Q分别为棱AD,AC的中点, 所以MQ∥CD. 又CD⊄平面MNQ,MQ⊂平面MNQ, 故CD∥平面MNQ. (2)因为M,N分别为棱AD,BD的中点,所以MN∥AB. 又AB⊥CD,AB⊥AD,故MN⊥AD,MN⊥CD. 因为AD∩CD=D,AD,CD⊂平面ACD, 所以MN⊥平面ACD. 又MN⊂平面MNQ,所以平面MNQ⊥平面ACD. 17.(1)若p为真:Δ=4-4m≥0,解得m≤1. 解得 -1 解得-1≤t≤1. 18.(1) f ′(x)=-3x2+6x+9,切线的斜率为9, 所以f(x)在x=2处的切线方程为 y-20=9(x-2),即9x-y+2=0. (2)令f ′(x)=-3x2+6x+9=0,得x=3(舍),或x=-1. 当x∈(-2,-1)时,f ′(x)<0,所以f(x)在x∈(-2,-1)时单调递减;当x∈(-1,2)时,f ′(x)>0,所以f(x)在x∈(-1,2)时单调递增.又f(-2)=2+a,f(2)=22+a, 所以f(2)>f(-2),因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,于是有 22+a=22,解得 a=0. 故f(x)=-x3+3x2+9x,因此f(-1)=-5, 所以函数f(x)在区间[-2,2]上的最小值为-5. (2)设A(x1,y1),B(x2,y2),则 由题意P(1,0),Q(2,0). ∴(x1-1,y1)∥(x2-1,y2), ∴x1y2-x2y1=y1-y2. =2(y1-y2)(y1+y2). 若y1=y2,则k1=k2=0,结论成立; 若y1≠y2,则x1y2+x2y1=2(y1+y2), (3)当直线l与y轴平行时,设直线l与椭圆相交于C,D两点. 如果存在定点Q满足条件,则有 所以Q在x轴上,可设Q点的坐标为(x0,0). 记直线AQ的斜率为k1,直线BQ的斜率为k2. 设A(x1,y1),B(x2,y2),则 ∴x1y2-x2y1=t(y1-y2). ∵(x1y2-x2y1)(x1y2+x2y1) =2(y1-y2)(y1+y2). 若y1=y2,则k1=k2=0; 易知,点B关于x轴对称的点B′的坐标为(-x2,y2), ∴kQA=kQB′,∴Q,A,B′三点共线, 由f ′(x)<0,得 (2)设φ(x)=f(x)-g(x)+a 当x∈(0,1)时,F′(x)>0;当x∈(1,+∞)时,F′(x)<0,所以F(x)在x∈(0,1)递增,在[1,+∞)上单调递减,∴F(x)max=F(1)=0. ∴对任意的x∈(0,+∞),恒有f(x)≤g(x),故不存在x0>1满足题意. 当k>1时,对于x>1,有f(x) 当k<1时,令G(x)=f(x)-kg(x),x∈(0,+∞)时,则有 由G′(x)=0,得-x2+(1-k)x+1=0, 当x∈(1,x2)时,G′(x)>0,故G(x)在[1,x2)内单调递增,从而当x∈(1,x2)时,G(x)>G(1)=0,即f(x)>k(x-1). 综上,k的取范围是(-∞,1).二、解答题(本大题共6小题,共计90分.解答应写出必要的文字说明、证明过程或演算步骤)
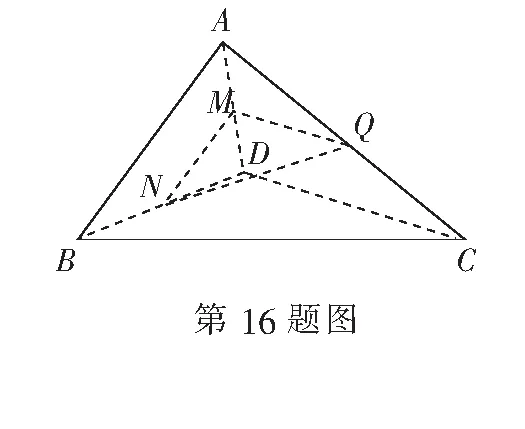
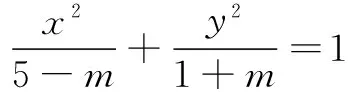
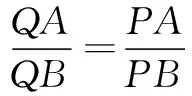
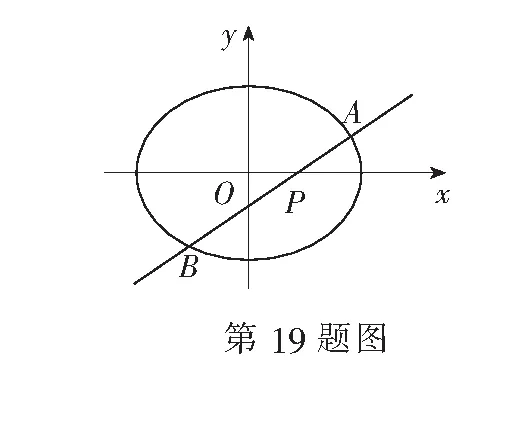
参考答案