探析几何关系代数化的有效策略——以2015年高考全国卷Ⅰ理科第20题为例

虞　懿　　　　　　　　　　　吴微庆

(浙江省金华市第六中学，321000)　(浙江省金华广播电视大学(浙江商贸学校)，321000)



○高考之窗○

探析几何关系代数化的有效策略
——以2015年高考全国卷Ⅰ理科第20题为例

虞懿吴微庆

(浙江省金华市第六中学，321000)(浙江省金华广播电视大学(浙江商贸学校)，321000)

解析几何的核心方法是用代数的方法研究图形的几何性质,核心思想是“数形结合”.2015年高考全国卷Ⅰ理科第20题,保持了全国卷背景熟悉、入口宽泛、解法多样的一贯风格,细细品读深感底蕴纯厚,紧扣解析几何的思想精髓.本文从解决解析几何问题的核心方法思想出发,探析该题第(2)问的解法.

一、试题展现

(1)当k=0时,分别求C在点M和N处的切线方程;

(2) y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.

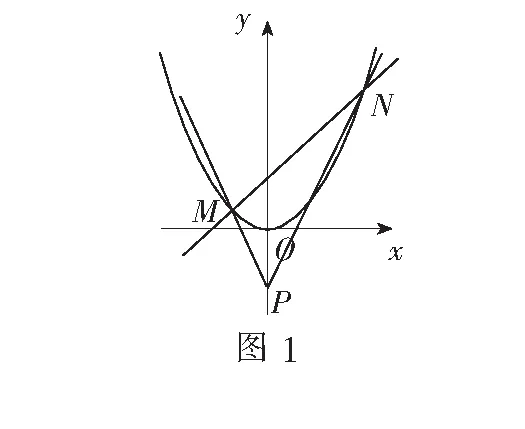
二、解法探析

对于第(2)问有以下几种求解策略.

策略1选择恰当形式,实现几何关系的代数表示

几何关系代数化是解决解析几何问题的关键.在本题中的几何关系是∠OPM=∠OPN,用什么样的代数关系来表示这个几何关系?对于直线与坐标轴所成角的问题,很自然地想到直线的倾斜角.解析几何中描述倾斜角的代数形式就是斜率,由此想到用斜率表示几何关系“∠OPM=∠OPN”,进而求出点P的坐标.

解法1设P(0,b)为符合题意的点,M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为k1,k2.

将y=kx+a代入C的方程，得

x2-4kx-4a=0，

故x1+x2=4k,x1x2=-4a，

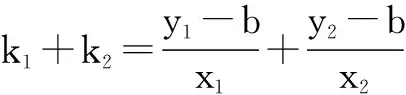
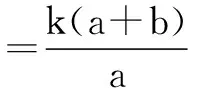
当b=-a时,有k1+k2=0,则直线PM的倾斜角与直线PN的倾斜角互补.

故∠OPM=∠OPN,所以点P(0,-a)符合题意.

设直线PM,PN的斜率分别为k1,k2，当k≠0时,有x1+x2≠0,于是

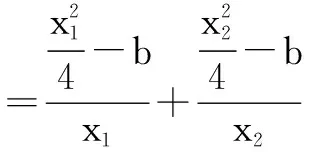
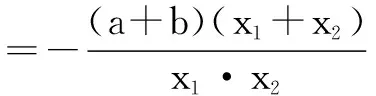
当b=-a时,有k1+k2=0,则直线PM的倾斜角与直线PN的倾斜角互补,故

∠OPM=∠OPN；

当k=0时,若b=-a,亦使得∠OPM=∠OPN.

综上,点P(0,-a)符合题意.

解法3直线y=kx+a(a>0)交y轴于点(0,a),则可设此直线为

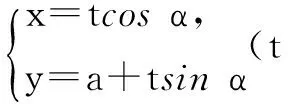
代入C的方程，得

cos2α·t2-4sinα·t-4a=0,

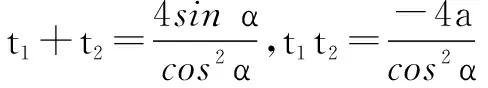
设P(0,b)为符合题意的点,M(t1cosα,a+t1sinα),N(t2cosα,a+t2sinα),直线PM,PN的斜率分别为k1,k2，于是

+2sinαcosα·t1t2]

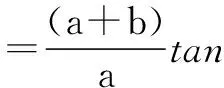
当b=-a时,有k1+k2=0,则直线PM的倾斜角与直线PN的倾斜角互补,故∠OPM=∠OPN,所以点P(0,-a)符合题意.

评注直线与抛物线的相交问题,解法1将抛物线与直线方程联立,利用韦达定理可简化运算,这是解析几何常见的解题思路.

近期， 有单位和读者向本刊反映， 有中介机构或网站宣称代理《草原与草坪》征集稿件， 并向投稿者收取费用，承诺可以在本刊发表文章，此举已对本刊声誉造成不良影响。对此， 本刊声明如下：

解法2借助抛物线的参数方程来设点,避免了方程的联立,简化了计算.

解法3利用直线的参数方程中参数的几何意义,避免了繁琐的计算,使得方程的联立简便易得.

策略2利用三角形内角平分线的性质定理,实现几何关系的代数表示

将y=kx+a代入C的方程，得x2-4kx-4a=0,则x1+x2=4k,x1·x2=-4a.

假设存在点P(0,b),使得当k变动时,总有∠OPM=∠OPN,则由角平分线分线段成比例定理，得

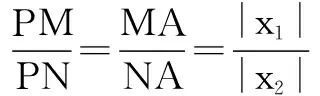
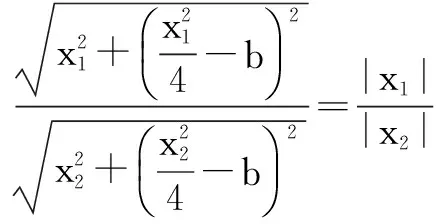
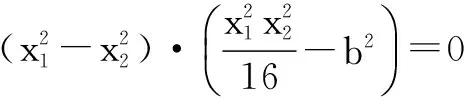
当b=a时,唯有k=0时成立,所以b=-a,故y轴上存在点P(0,-a)符合题意.

评注这里巧用三角形内角平分线的性质定理探讨a与b的相互关系,简化了代数运算过程，体现了代数与几何的完美结合.

策略3构造对称点,实现几何关系的代数表示

对称是平面几何中重要的几何关系,对称图形中包含很多相等的几何量和某些特殊的几何图形,如角、线段、角平分线、线段的垂直平分线等,为解决本题打开了更广阔的思路.

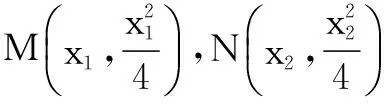
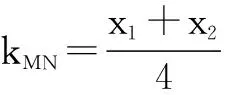
于是直线MN的方程为

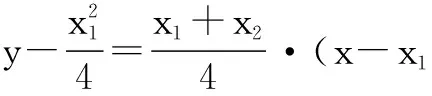
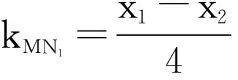
于是直线MN1的方程为

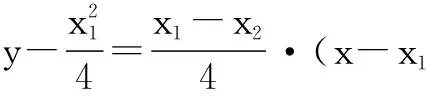
评注数学美无处不在,最常见的有简单美、对称美、定值定点美等.本解法通过构造点N关于y轴的对称点N1,寻找对称后的代数关系,这本身就是创造美、发现美的过程.

策略4回归向量知识本质,实现几何关系的代数表示

向量具有代数、几何双重身份,融数形于一体,是沟通代数和几何的桥梁.它可以将几何问题坐标化、数量化,因此它是解决解析几何问题的重要工具.

解法6设P(0,b)为符合题意的点,M(x1,y1),N(x2,y2).

当k≠0时,有x1+x2≠0,将y=kx+a代入C的方程，得

x2-4kx-4a=0，

故x1+x2=4k,x1·x2=-4a.

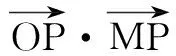
=b(b-y1),

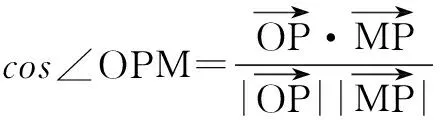
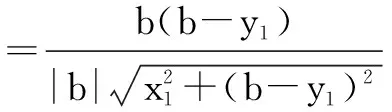
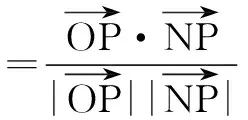
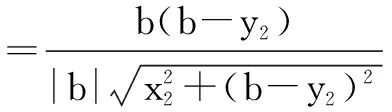
若cos∠OPM=cos∠OPN,则

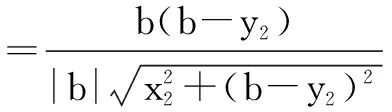
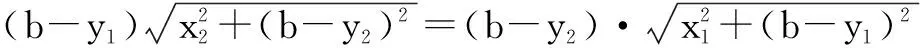
化简得b2=a2,即b=-a或b=a(舍).

从而当b=-a时,有cos∠OPM=cos∠OPN,即∠OPM=∠OPN.

当k=0时,若b=-a,亦使得∠OPM=∠OPN.

综上,点P(0,-a)符合题意.

评注本解法另辟蹊径,构建平面向量,利用数量积的定义求夹角,简洁明了.在探究解题思路时,要善于从不同的角度分析、挖掘它与其他知识的联系,在平面解析几何中有关长度、角度的计算及有关平行、三点共线、垂直等位置关系问题都可以用向量知识解决.

三、解题启示

解析几何的核心方法是用代数的方法研究几何问题.在解题过程中,首先要将文字信息、图形条件进行转换,通过代数语言描述几何要素及其关系,将已知的几何条件表示成代数式,然后进行适当的代数运算得出代数结果,最后通过分析代数结果的几何含义解决几何问题.在这个过程中要经历文字信息、图形特征和符号语言之间的多重转换,因此,我们必须重视对几何关系的深入研究,探究用何种代数形式能恰当表示题目中的几何关系,同时有利于代数运算,从而形成正确的解题策略.

三角形内角平分线的性质定理:三角形的内角平分线内分对边成两条线段,那么这两条线段与这个角的两边对应成比例.