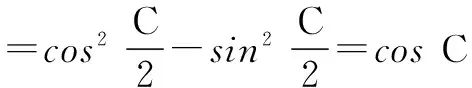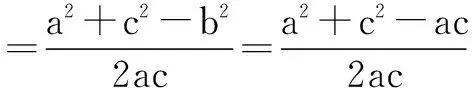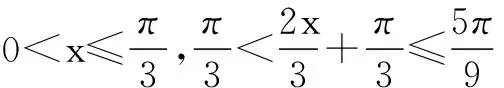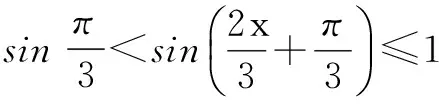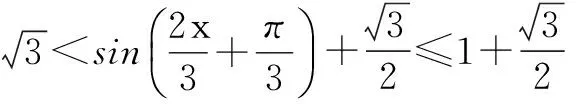例析正、余弦定理在解三角形中的应用

王　艳

(宁夏银川市第二十四中学,750021)



例析正、余弦定理在解三角形中的应用

王艳

(宁夏银川市第二十四中学,750021)

正、余弦定理是学习有关三角知识的继续和发展,它深入揭示了三角形边与角之间的关系,在各个方面有着广泛的应用.现将其在解三角形中的综合应用例析如下,望读者能更全面地理解该思想,从而灵活掌握相关技巧．

一、用正弦定理解三角形

思路本题由正弦定理出发,将边化为角,再结合三角恒等变换来解决．

解∵a+c=2b,

∴sinA+sinC=2sinB,

(*)

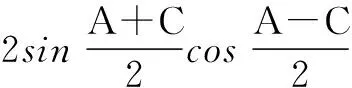
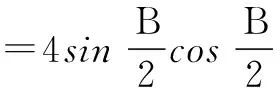
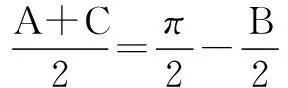
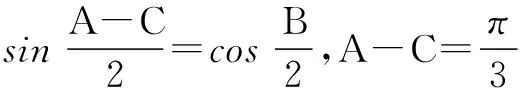
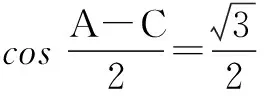
∴(*)式即为

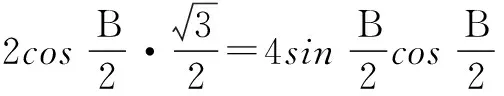
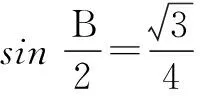
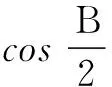
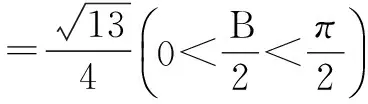
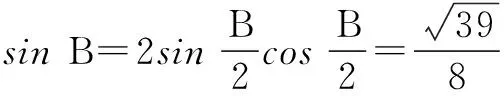
评注处理边角混合问题一定要注意确定解的个数,做到准确无误．

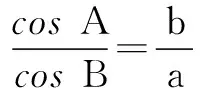
∴sinBcosB=sinAcosA,

∴sin2A=sin2B,

∴2A=2B或2A+2B=π,

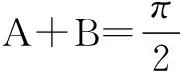
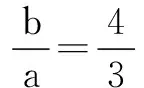
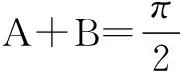
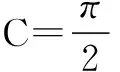
得9k2+16k2=102,

解得k=2,a=6,b=8．

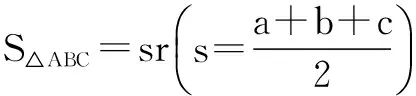
评注本题也考察正弦定理的灵活应用,但要注意sin2A=sin2B⟹2A=2B或2A+2B=π这一结论的准确运用．

二、用余弦定理解三角形

例3在∆ABC中,A最大,C最小,且A=2C,a+c=2b,求此三角形三边之比.

解由正弦定理，得

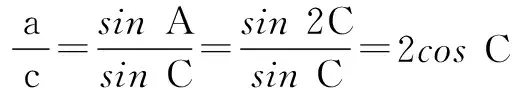
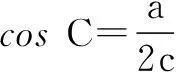
由余弦定理，有

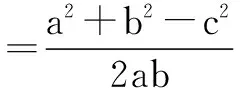
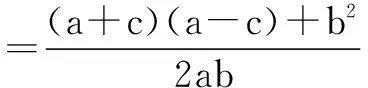
而a+c=2b，

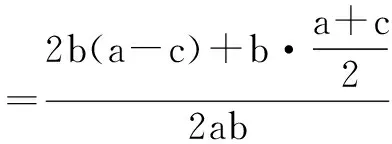
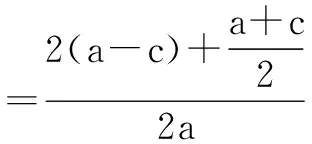
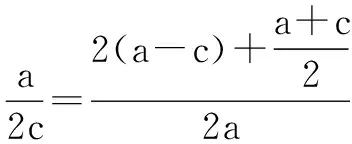
整理得2a2-5ac+3c2=0，

∵A=2C,∴a=c不成立，

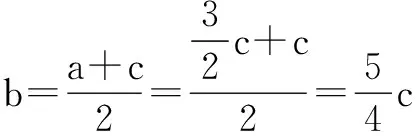
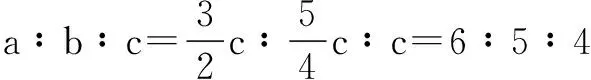
故此三角形三边之比为6∶5∶4．

评注对于余弦定理要牢记各种表示形式.

三、判断三角形的形状及证明恒等式

例4在∆ABC中， 若b2sin2C+c2sin2B=2bccosBcosC,试判断三角形的形状.

思路本题可用两种不同的方法来处理,最终殊途同归．

解法1由正弦定理，得

其中R为∆ABC外接圆的半径，于是有

8R2sin2Bsin2C=8R2sinBsinCcosBcosC．

又∵sinBsinC≠0,

∴sinBsinC=cosBcosC,

∴cos(B+C)=0, 从而B+C=90°，所以∆ABC为直角三角形．

解法2将已知等式变形为

b2(1-cos2C)+c2(1-cos2B)

=2bccosBcosC．

于是由余弦定理，得

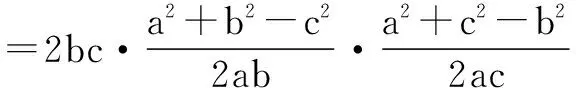
化简得b2+c2

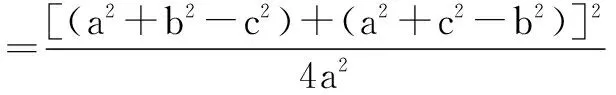
∴b2+c2=a2,

所以∆ABC为直角三角形.

评注不管选用哪种方法作出发点，都要注意正确运用相关公式.

例5已知A,B,C为∆ABC的三个内角, 并且(sinA+sinB)2-sin2C=3sinAsinB. 求证:A+B=120°．

思路由于A+B+C=180°,所以可以将问题转化为证明C=60°． 观察已知条件为三角函数关系,因此应该考虑向三角函数方向转化,只需求得角C的三角函数值即可．

证明由(sinA+sinB)2-sin2C=3sinAsinB，得到

sin2A+sin2B-sin2C=sinAsinB.

又由正弦定理

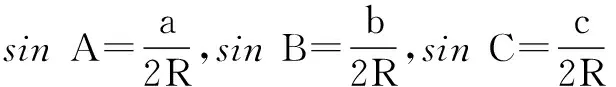
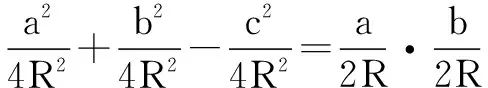
即a2+b2-c2=ab,

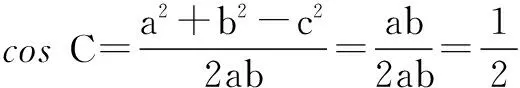
又0°

∴C=60°,A+B=180°-C=120°.

评注在利用正、余弦定理证明有关三角恒等式和判定三角形的形状时，主要是将已知条件中边角关系转化为角或边的关系.一般地，利用正弦定理可将边转化为角，利用余弦定理可将角转化为边的关系，从而进一步解决问题.

四、求三角形的面积

例6在∆ABC中,

求(1)角C的度数；

分析结合平面向量的夹角公式,求出角C,再由余弦定理结合面积,即可求出a+b的值．

(2)由c2=a2+b2-2abcosC，得

(*)

评注本题考察了余弦定理与平面向量的综合应用,渗透了解题方法及一定的数学思想应多加注意．

五、正、余弦定理的综合应用

例7已知函数

(1)将f(x)写成Asin(ωx+φ)+B的形式，并求其图象的对称中心的横坐标；

(2)如果∆ABC的三边a,b,c满足b2=ac,且边b所对的角为x,试求x的范围以及此时函数f(x)的值域.

(2)∵b2=ac,

评注由b2=ac联想到余弦定理的应用，不等式的应用是解决此题的关键.

正、余弦定理还可以与许多其它知识点交汇形成具有一定综合性的问题,在此不再一一列举了,同学们应在今后的学习中多加注意和积累．

解决此类问题的基本方法有两种：一是化边为角，二是化角为边.