含量词的导数问题的求解策略

温展平

(广东省兴宁市第一中学,514500)



含量词的导数问题的求解策略

温展平

(广东省兴宁市第一中学,514500)

导数题是高考题中的常客,而且大都以压轴题的面目出现,所以拿下导数题是迈入高分段的标志．导数题虽年年有,但却悄然之中发生着些改变．这其中,尤以关于“任意”、“存在”的内容最为明显．“任意”、“存在”可以说是导数题最为明显的特色,从早期单一型,发展到现今的混合型．本文对此作一归纳．

一、单一函数单一“任意”型

例1已知函数f(x)=x-ln(x+a)的最小值为0,其中a>0．

(1)求a的值;

(2)若对任意的x∈[0,+∞),有f(x)≤kx2成立,求实数k的最小值．

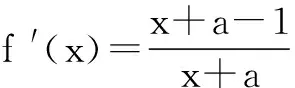
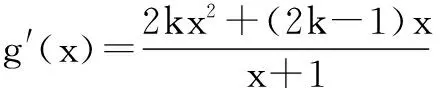
评注“任意”的意思是不管x取给定集合中的哪一个值,得到的函数值都要满足给定的不等式.它有两种形式:“对任意的x∈A,a≥f(x)恒成立”等价于“当x∈A时,a≥f(x)max”;“对任意的x∈A,a≤f(x)恒成立”等价于“当x∈A时,a≤f(x)min”．

二、单一函数单一“存在”型

例2已知函数f(x)=alnx+x2(a∈R),若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围．

解f(x)≤(a+2)x⟹a(x-lnx)≥x2-2x.∵x∈[1,e],∴lnx≤1≤x且等号不能同时取,所以lnx0,因而

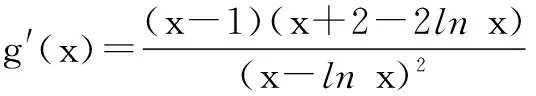
当x∈[1,e]时,x-1≥0,lnx≤1,x+2-2lnx>0,从而g′(x)≥0(仅当x=1时取等号),所以g(x)在[1,e]上为增函数,故g(x)的最小值为g(1)=-1,所以a的取值范围是[-1,+∞).

评注“存在”的意思是x取遍给定集合中的每一个值,都至少有一个函数值满足给定的不等式,它有两种形式:“存在x∈A,使得a≥f(x)成立”等价于“当x∈A时,a≥f(x)min”;“存在x∈A,使得a≤f(x)成立”等价于“当x∈A时,a≤f(x)max”．

三、单一函数双“任意”型

例3已知函数

f(x)=(a+1)lnx+ax2+1.

(1)讨论函数f(x)的单调性;

(2)设a<-1，如果对任意x1,x2∈(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|,求a的取值范围．

解(1)f(x)的定义域为(0,+∞)，

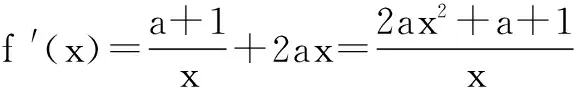
当a≥0时，f ′(x)>0,故f(x)在(0,+∞)单调递增.

当a≤-1时，f ′(x)<0,故f(x)在(0,+∞)单调递减.

(2)不妨假设x1≥x2,而a<-1,由(1)知f(x)在(0,+∞)单调递减，从而∀x1,x2∈(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|等价于∀x1,x2∈(0,+∞),有

f(x2)+4x2≥f(x1)+4x1.

(*)

评注对本题，容易得出(|f(x1)-f(x2)|)max≥(4|x1-x2|)min的不等价转换错误．如果注意到等式两边都有变量x1,x2,一边变化会引起另一边变化,这种情况要将等式两边移至一边,通过分离变量x1,x2,就可方便构造新的函数，以达到解题的目的．

四、单一函数双“存在”型

例4设x=3是函数f(x)=(x2+ax+b)e3-x(x∈R)的一个极值点．

(1)求a与b的关系式(用a表示b),并求f(x)的单调区间;

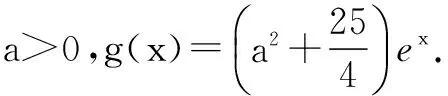
解(1)f ′(x)=-[x2+(a-2)x+b-a]e3-x,则f ′(3)=0,解得b=-3-2a．又f ′(x)=-[x2+(a-2)x-3-3a]e3-x=-(x-3)(x+a+1)e3-x,令f ′(x)=0,得x1=3,x2=-a-1.由于x=3是极值点,所以-a-1≠3,a≠-4．所以当a<-4时,-a-1>3,f(x)在(-∞,3)单调递减,在(3,-1-a)单调递增,在(-1-a,+∞)单调递减;当a>-4时,-a-1<3,f(x)在(-∞,-1-a)单调递减,在(-1-a,3)单调递增,在(3,+∞)单调递减．

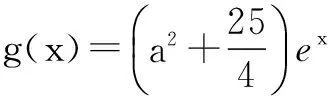
评注“存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1”等价于“|f(x1)-g(x2)|min<1”,而|f(x1)-g(x2)|min要通过f(x)与g(x)的值域来得到．

五、双函数“任意”+“存在”型

解题意等价于f(x)在(0,1)内的最大值大于或等于g(x)在[1,2]上的最大值．

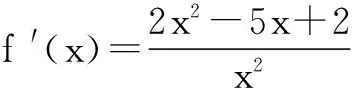
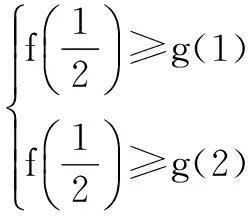
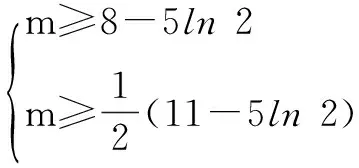
评注∃x1∈A,∀x2∈B,使得f(x1)≥g(x2)成立⟺f(x)max≥g(x)max；同样,∀x1∈A,∃x2∈B,使得f(x1)≥g(x2)成立⟺f(x)min≥g(x)min．

六、双函数“任意”+“任意”型

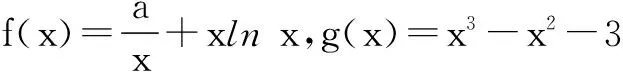
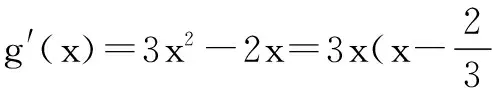
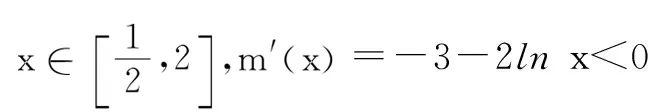
评注∀x1∈A,∀x2∈B,使得f(x1)≥g(x2)成立⟺f(x)min≥g(x)max

七、双函数“存在”+“存在”型

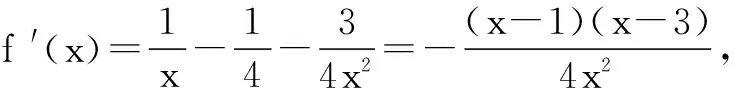
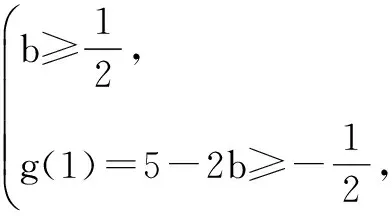
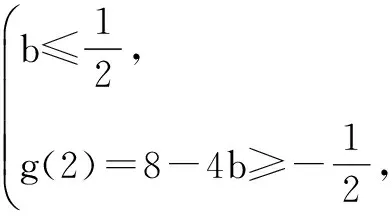
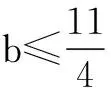
评注∃x1∈A,∃x2∈B,使得f(x1)≤g(x2)成立⟺f(x)min≤g(x)max；同样∃x1∈A,∃x2∈B,使得f(x1)≥g(x2)成立⟺f(x)max≥g(x)min．

从以上例题可以看出,导数题的发展轨迹是从单一函数往双函数发展,从单一变量往双变量甚至是多变量发展,从单一任意或存在往任意存在混合上发展．但不管怎样发展,它们的基础还是单函数的任意与存在性问题．面对两个或多个变量的时候,常常先把其中的一个当成是变量,其它的当成是常量,这样就把问题转化为单变量的常规题了．这里同样可以采取类似的方法,在f(x1)和g(x2)中,依次把一个当成是常量,另一个当成是变量,这样就把问题转化成了前面熟悉的单函数单任意(或存成)题了．比如“∀x1∈A,∃x2∈B,使得f(x1)≥g(x2)成立”,就可以先把f(x1)当成是常量,“∃x2∈B,使得f(x1)≥g(x2)成立”等价于f(x1)≥g(x2)min；反过来,再把g(x2)当成是常量,“∀x1∈A,使得f(x1)≥g(x2)成立”等价于f(x1)min≥g(x2).综合以上两方面,就得出了“∀x1∈A,∃x2∈B,使得f(x1)≥g(x2)成立⟺f(x)min≥g(x)min”的正确结论．

1.线性规划视角

分析求解本题的难点是如何去掉绝对值符号.首先我们发现当x2+y2≤1时,6-x-3y≥0,所以|2x+y-2|+|6-x-3y|=|2x+y-2|+6-x-3y.为了求F的最小值,我们可以按2x+y-2>0与2x+y-2≤0,把问题转化为约束条件(x2+y2≤1及2x+y-2>0或2x+y-2≤0)下,求F的最小值.