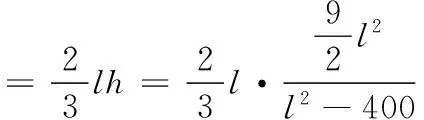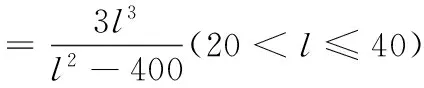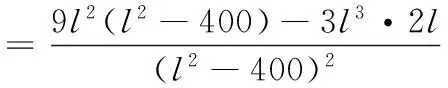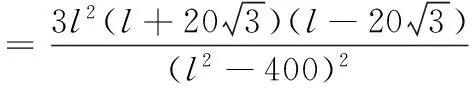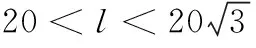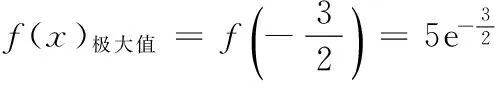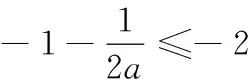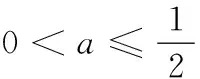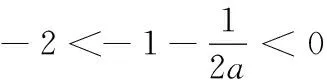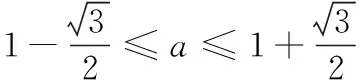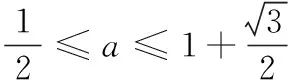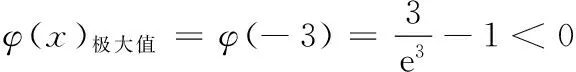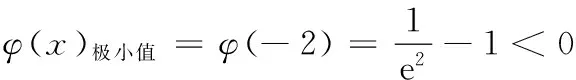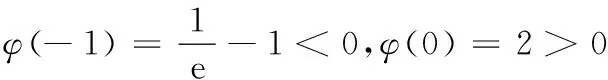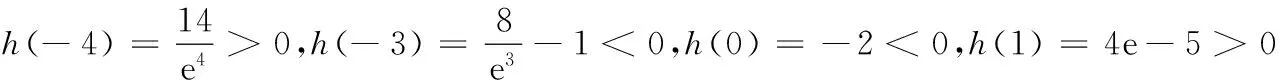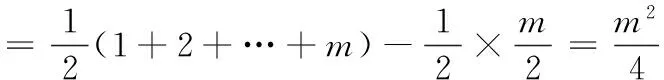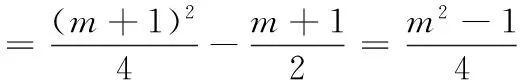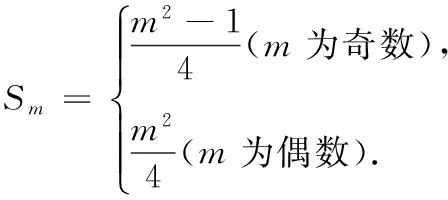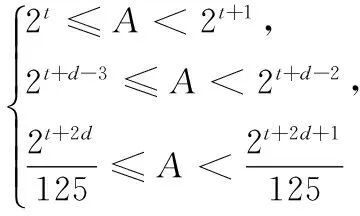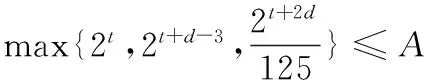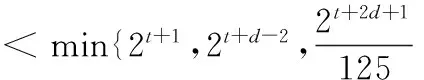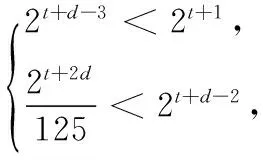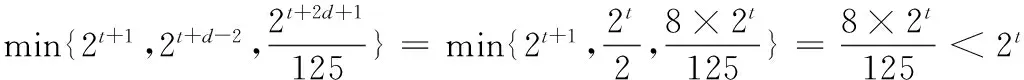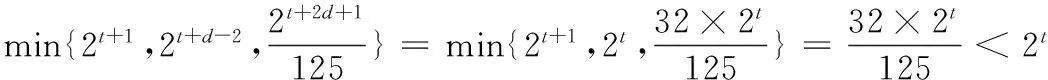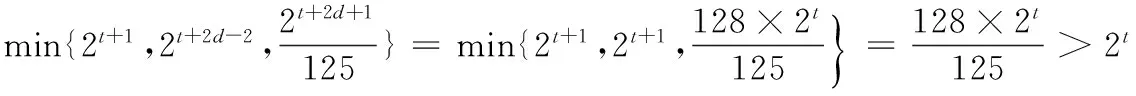高三数学综合测试



高三数学综合测试

一、填空题(本大题共14小题,每小题5分,共70分)

1.已知集合A={x|x2-2x<0},B={0,1,2},则A∩B=______.

2.若复数z=i(3-2i)(i是虚数单位),则z的虚部为______.

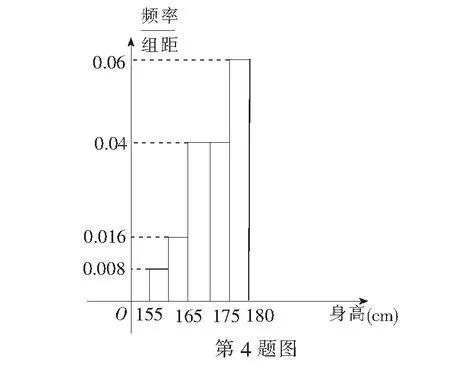
4.某学校从高三年级共800名男生中随机抽取50名测量身高.据测量被测学生身高全部介于155 cm和195 cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165)、…第八组[190,195],按上述分组方法得到的频率分布直方图的一部分如图所示.估计这所学校高三年级全体男生身高180 cm以上(含180 cm)的人数为______.

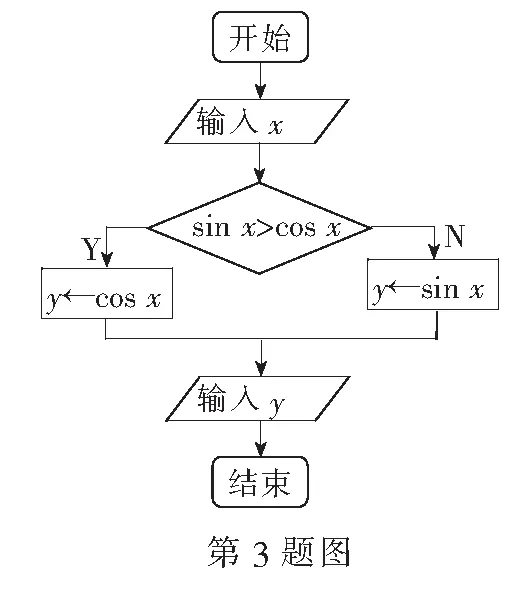
6.从1,2,3,4,5这5个数中,随机抽取2个不同的数,则这2个数的和为偶数的概率是______.

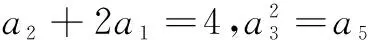
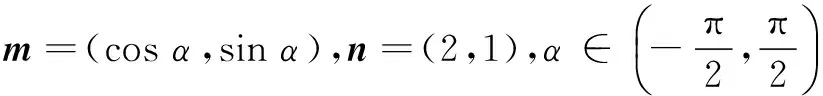
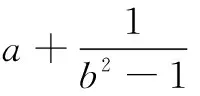
12.已知圆O:x2+y2=4,若不过原点O的直线l与圆O交于P、Q两点,且满足直线OP,PQ,OQ的斜率依次成等比数列,则直线l的斜率为______.

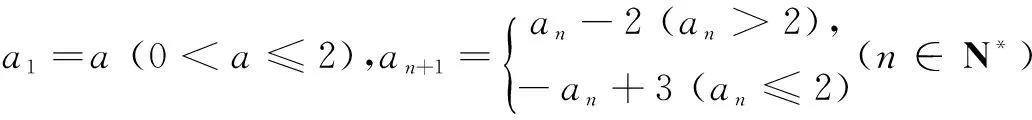
二、解答题(本大题共6小题,共计90分,解答时应写出必要的文字说明、证明过程或演算步骤)

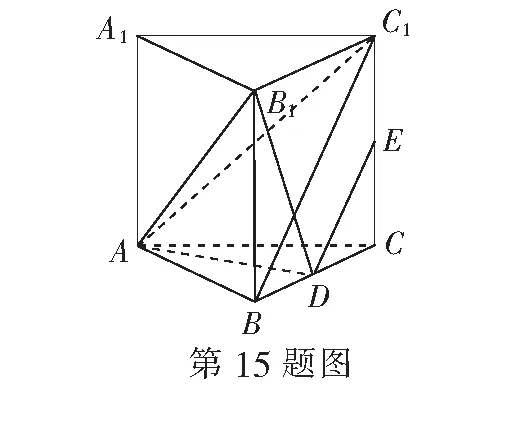
15.(本小题满分14分)如图,已知直三棱柱ABC-A1B1C1中,AB=AC，D、E分别为BC、CC1中点，BC1⊥B1D.

(1)求证:DE∥平面ABC1;

(2)求证:平面AB1D⊥平面ABC1.

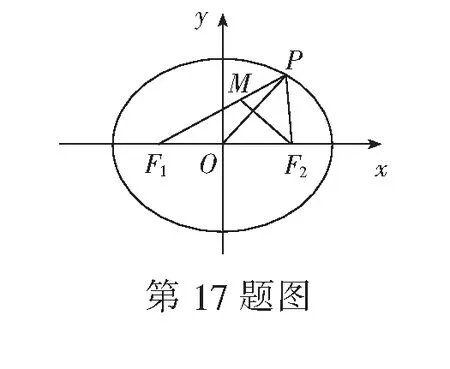
(2)若λ=2,求椭圆离心率e的取值范围.

18.(本小题满分15分)某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy.

(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?

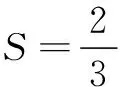
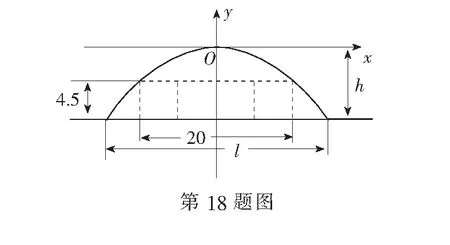
19.(本小题满分16分)已知函数f(x)=(ax2+x+2)ex(a>0),其中e是自然对数的底数).

(1)当a=2时，求f(x)的极值；

(2)若f(x)在[-2,2]上是单调增函数,求a的取值范围;

(3)当a=1，求整数t的所有值,使方程f(x)=x+4在[t,t+1]上有解.

20.(本小题满分16分)若数列{an}中不超过f(m)的项数恰为bm(m∈N*)，则称数列{bm}是数列{an}的生成数列，称相应的函数f(m)是数列{an}生成{bm}的控制函数.

(1)已知an=n2,且f(m)=m2,写出b1,b2,b3;

(2)已知an=2n,且f(m)=m,求{bm}的前m项和Sm;

(3)已知an=2n,且f(m)=Am3(A∈N*),若数列{bm}中，b1,b2,b5是公差为d(d≠0)的等差数列，且b3=10,求d的值及A的值.

参考答案

一、填空题

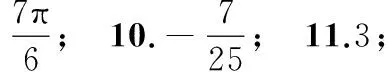
二、解答题

15.(1)∵D、E分别为BC、CC1中点，

∴DE∥BC1.

∵DE⊄平面ABC1,BC1⊂平面ABC1.

∴DE∥平面ABC1.

(2)直三棱柱ABC-A1B1C1中，

CC1⊥平面ABC,∵AD⊂平面ABC，

∴CC1⊥AD.∵AB=AC，D为BC中点，

∴AD⊥BC.又∵CC1∩BC=C，CC1,BC⊂平面BCC1B1，

∴AD⊥面BCC1B1,

∵BC1⊂平面BCC1B1,

∴AD⊥BC1,

又∵BC1⊥B1D,B1D∩AD=D,

B1D,AD⊂平面AB1D,

∴BC1⊥平面AB1D.

∵BC1⊂平面ABC1,

∴平面AB1D⊥平面ABC1.

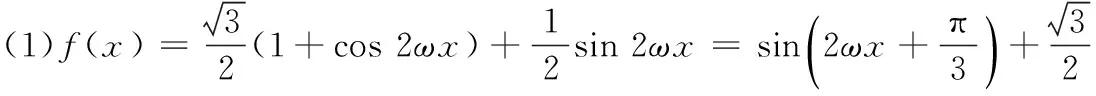
∵f(x)的周期为π，且ω>0,

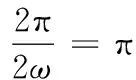
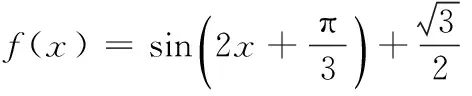
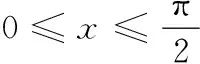
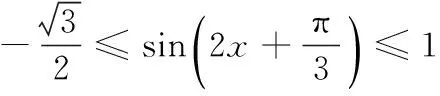
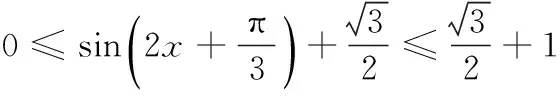
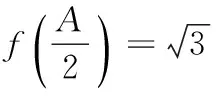
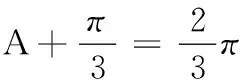
由余弦定理，知a2=b2+c2-2bccos A,即

16=b2+c2-bc,

∴ 16=(b+c)2-3bc.

因为b+c=5,所以bc=3,

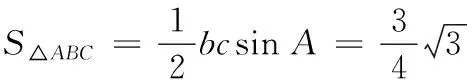
∴F1(-2,0),F2(2,0),

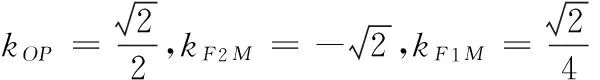
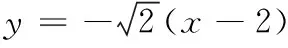
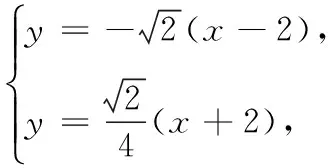
(2)设P(x0,y0),M(xM,yM),

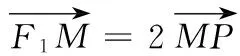
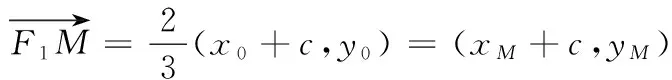
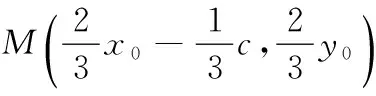
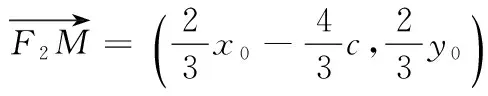
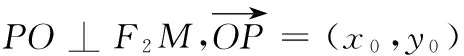
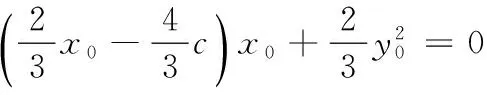
即 x20+y20=2cx0.

c2x20-2a2cx0+a2(a2-c2)=0,

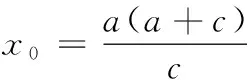
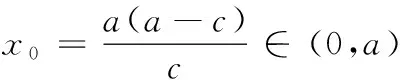
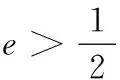
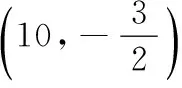
令y=-6,解得x=±20,则隧道设计的拱宽l是40米.

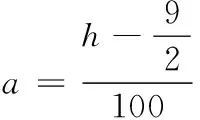
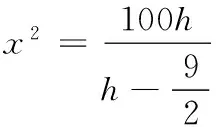
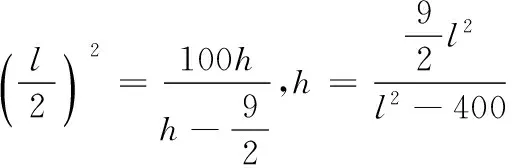
即 20

19.(1)f(x)=(2x2+x+2)ex,则

f ′(x)=(2x2+5x+3)ex

=(x+1)(2x+3)ex,

x-∞,-32()-32-32,-1()-1(-1,+∞)f'(x)+0-0+f(x)增极大值减极小值增

f(x)极小值=f(-1)=3e-1.

(2)问题转化为f ′(x)=[ax2+(2a+1)x+3]ex≥0在x∈[-2,2]上恒成立.

又ex>0,即ax2+(2a+1)x+3≥0在x∈[-2,2]上恒成立.

令g(x)=ax2+(2a+1)x+3,

∴Δ=(2a+1)2-12a≤0,

(3)∵a=1,设h(x)=(x2+x+2)ex-x-4,

则 h′(x)=(x2+3x+3)ex-1.

令φ(x)=(x2+3x+3)ex-1,则

φ′(x)=(x2+5x+6)ex,

令φ′(x)=(x2+5x+6)ex=0,得

x=-2,-3.

∴存在x0∈(-1,0),x∈(-∞,x0)时，φ(x)<0,x∈(x0,+∞)时，φ(x)>0,

∴h(x)在(-∞,x0)上单调减，在(x0,+∞)上单调增.

由零点的存在性定理，可知h(x)=0的根x1∈(-4,-3),x2∈(0,1),即t=-4,0.

20.(1)m=1,则a1=1≤1,

∴b1=1;m=2,则a1=1<4,a2=4≤4,∴b2=2,m=3,则a1=1<9,a2=4<9,a3=9≤9,∴b3=3.

m为偶数时，

Sm=b1+b2+…+bm

m为奇数时，

Sm=b1+b2+…+bm

=Sm+1-bm+1

(3)依题意，有an=2n,f(1)=A,f(2)=8A,f(5)=125A.设b1=t,即数列{an}中，不超过A的项恰有t项，所以2t≤A<2t+1.

同理2t+d≤8A<2t+d+1,2t+2d≤125A<2t+2d+1,

∵d为正整数，∴d=1,2,3.

∴t+3≤b3≤t+6.