具测量误差和缺失数据指数分布参数的估计与检验

赵志文, 何静花, 杨慧超

(吉林师范大学 数学学院, 吉林 四平 136000)



具测量误差和缺失数据指数分布参数的估计与检验

赵志文, 何静花, 杨慧超

(吉林师范大学 数学学院, 吉林 四平 136000)

在寿命实验中,由于测量设备的局限性,观测方法以及环境等因素的影响,观测数据经常存在测量误差。对带有测量误差的数据进行估计时,若忽略测量误差,可能导致估计是不相合的。此外,在许多实际问题的研究中,一些观测值经常无法观测而缺失。针对指数分布总体,利用矩估计的方法给出了未知参数的估计,证明了估计的优良性,讨论了两指数分布总体参数相等的假设检验,给出了检验统计量及其极限分布,得到了两总体参数之差的置信区间,并且用随机模拟的方法说明了方法的可行性。

指数分布; 缺失数据; 测量误差; 矩估计; 假设检验

0 引 言

统计学中,具有测量误差和缺失数据的观测数据得到越来越多的关注与研究。文献[1-3]讨论了存在测量误差下的参数估计。文献[4]研究了具有部分缺失数据的两指数总体的参数估计以及相关的检验问题。文献[5]讨论了定时截尾下具有部分缺失数据的2个指数总体的参数估计及相关假设检验问题。文献[6]研究了两参数指数失效模型的参数估计问题。本文进一步讨论了当样本具有测量误差和部分数据缺失时,2个指数分布总体参数的估计问题与相关假设检验问题。给出了参数的矩估计,证明了估计的优良性,讨论了两指数分布总体参数相等的假设检验,给出了检验统计量及其的极限分布,并且用随机模拟的方法说明了本方法的可行性。

1 矩估计及其渐进性质

对于如上参数λi(i=1,2)的矩估计,有下面的相合性和渐近正态性。

2 两总体参数相等的检验以及两总体参数之差的渐近置信区间

在实际问题中,人们通常关心2组样本是否来自同一个总体,这一问题可以归结为检验2个总体参数相等的问题。现在考虑假设检验:H0:λ1-λ2=0↔λ1-λ2≠0。

3 随机模拟

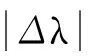
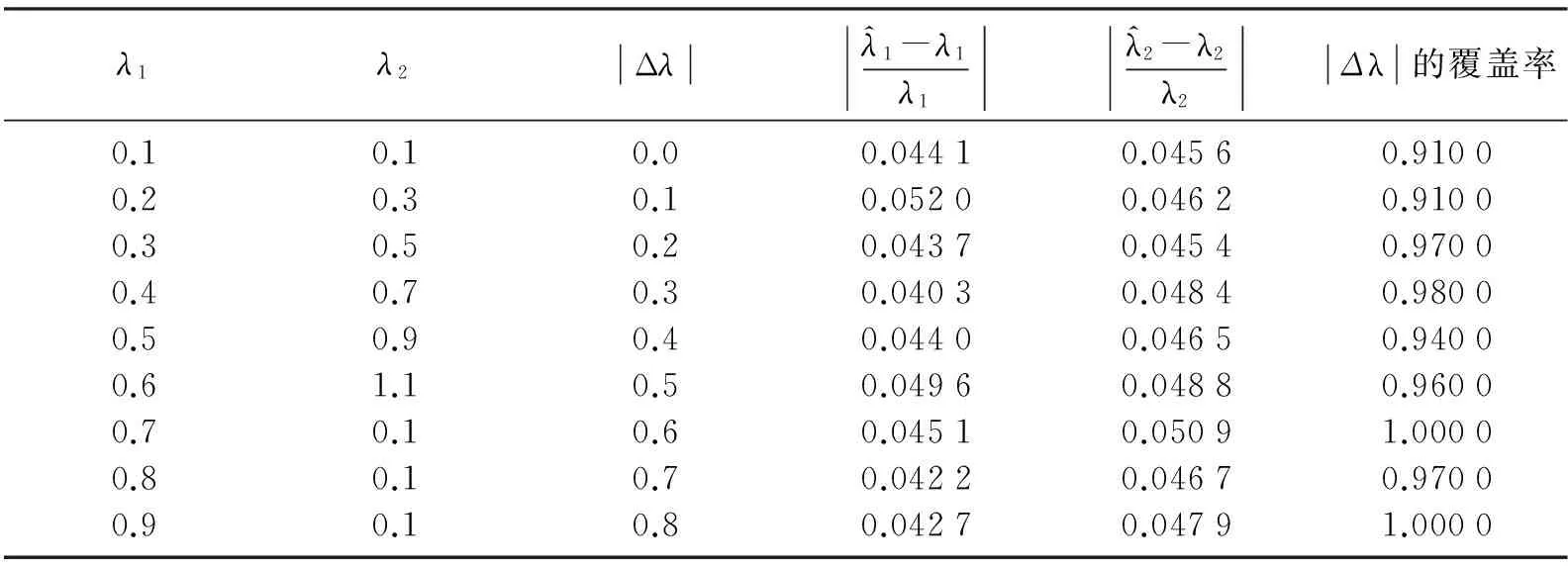
表1 估计的相对偏差与置信区间的覆盖率

[1]张征宇,朱平芳. 有测量误差时空间自回归模型的估计与检验[J]. 统计研究, 2010,27(4):103-109.

[2]李德旺. 广义线性测量误差模型的贝叶斯统计分析[D]. 昆明:云南大学, 2015.

[3]RODDAM A W. Measurement error in nonlinear models: a modern perspective[J]. J R STAT SOC, 2008,171(2):505-506.

[4]刘银萍. 具部分缺失数据两个指数总体的估计和检验[J]. 吉林大学学报(理学版), 2002,40(3):255-257.

[5]赵志文,王思洋,王瑞庭,等. 定时截尾下具有部分缺失数据两个指数总体参数的估计与检验[J]. 吉林大学学报(理学版), 2009,47(1):26-30.

[6]KHATTREE R. Estimation of guarantee time and mean life after warranty for two-parameter exponential failure model[J]. Austral J Statist, 1992,34:207-215.

[7]茆诗松,王静龙,濮小龙. 高等数理统计[M]. 北京:高等教育出版社, 2000:116-118.

Parameterestimation and hypothesis testing of exponential distribution with measurement error and missing date

ZHAOZhiwen,HEJinghua,YANGHuichao

(College of Mathematics, Jilin Normal University, Siping 136000, China)

In life test, observation data have measurement errors due to various factors such as the limitations of measuring equipment, observation methods and the environment. The estimation will not be consistent if we ignore the measurement errors. Moreover, for many practical problems, some data are often not observable and missing. In this paper, for the exponential population, the moment estimation of the exponential distribution population parameters is obtained, the properties of the estimation are proved and the confidence interval of the difference of the two population parameters is established. Furthermore, a simulation study is also conducted to show the feasibility of the proposed methods.

exponential distribution; missing date; measurement error; moment estimation; hypothesis testing

2015-12-29。

吉林省科技发展计划项目(201201082)。

赵志文(1976-),男,吉林梨树人,吉林师范大学副教授,博士。

1673-5862(2016)02-0193-03

统计学

O212.1

A

10.3969/ j.issn.1673-5862.2016.02.014