和声蛙跳算法在复杂优化问题中的应用研究
2016-11-29肖文显王俊阁马孝琴
肖文显, 王俊阁, 马孝琴
(河南科技学院 网络中心, 河南 新乡 453003)
和声蛙跳算法在复杂优化问题中的应用研究
肖文显*, 王俊阁, 马孝琴
(河南科技学院 网络中心, 河南 新乡 453003)
和声搜索算法在求解复杂优化问题时,仅仅通过随机的方式产生新元素,搜索过程中新个体的有效性难以持续保证,影响算法的优化性能.针对该问题,将混合蛙跳算法的族群内部局部寻优模块嵌入和声搜索的算法框架中,将和声搜索算法的随机性与混合蛙跳算法的导向性相耦合.定义算法自适应调整参数并以此为基础对两种算法进行动态调用,从而实现两种算法的耦合动态搜索.将改进算法应用于标准测试函数和车辆路径问题的优化,模拟计算结果表明:本文提出的改进算法具有更强的全局搜索能力,得到的解更优,适合用于求解复杂优化问题.
优化问题; 和声搜索算法; 混合蛙跳算法; 耦合搜索; 动态平衡
和声搜索算法[1](Harmony Search,HS)是由Geem于2001年根据音乐家通过调整声调获得和声的原理提出的启发式搜索算法.HS算法具有参数少、收敛快等特点,被广泛应用于各种优化问题[2-4].但是,由于和声搜索算法的寻优过程是以随机的方式产生新元素,因此在求解复杂优化问题时,算法进化后期难以保障新元素的有效性,降低了算法的寻优性能,容易导致算法记忆库难以更新甚至早熟收敛.
针对该问题,本文借鉴混合蛙跳算法[5-6](Shuffled Frog Leaping Algorithm,SFLA)的族群内部局部寻优思想,将族群内部寻优模块作为一个子部分嵌入和声搜索算法当中,利用混合蛙跳算法的族群导向性搜索弥补和声搜索算法单纯随机性的缺陷.同时,定义算法自适应调整参数,并以该参数动态调用两算法,从而实现搜索机制的动态调整.
1 和声蛙跳算法
1.1 基本和声搜索算法
和声搜索算法是一种模仿音乐家创作乐曲过程的随机搜索算法,主要有记忆选择、局部调整、随机生成3种进化操作.和声搜索算法的主要参数包括:记忆库规模NP、问题维度D、记忆选择概率HMCR、局部调整概率PAR、调整步长BW等.
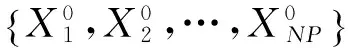

(1)
其中,xmax,j和xmin,j分别为待求解问题第j维的取值上限和下限;rand()为0~1之间随机分布的随机数;i=1,2,…,NP;j=1,2,…,D.
(2)
通过记忆选择产生的中间试验记忆库再以局部调整概率PAR进行局部调整,如式(3)所示:
(3)
1.2 算法的改进策略
和声搜索算法的寻优过程是以随机的方式产生新元素,这种寻优搜索模式无法保证算法在进化后期产生新元素的有效性,容易导致算法早熟收敛.为克服和声搜索算法这一缺陷,本文从算法的搜索机制和调整机制两个方面对算法进行改进.
1.2 .1互补搜索机制 本文将混合蛙跳算法嵌入和声搜索算法之中,利用混合蛙跳算法具有导向性的搜索特性,弥补和声搜索算法的不足,从而实现随机性和导向性之间的互补和平衡.
互补搜索的核心思想是将和声搜索算法和混合蛙跳算法相结合,即当随机因子小于选择概率HMCR时,算法进入和声搜索算法框架,从原记忆库中随机选择现有音乐记忆;当随机因子大于选择概率HMCR时,算法进入混合蛙跳算法框架,将原种群按照个体适应值优劣进行排序并顺次分配进入不同的族群,按式(4)、(5)在每个族群内部进行局部寻优:

(4)

(5)
互补搜索机制如图1所示.其中,R1、R2为0~1之间的随机数.
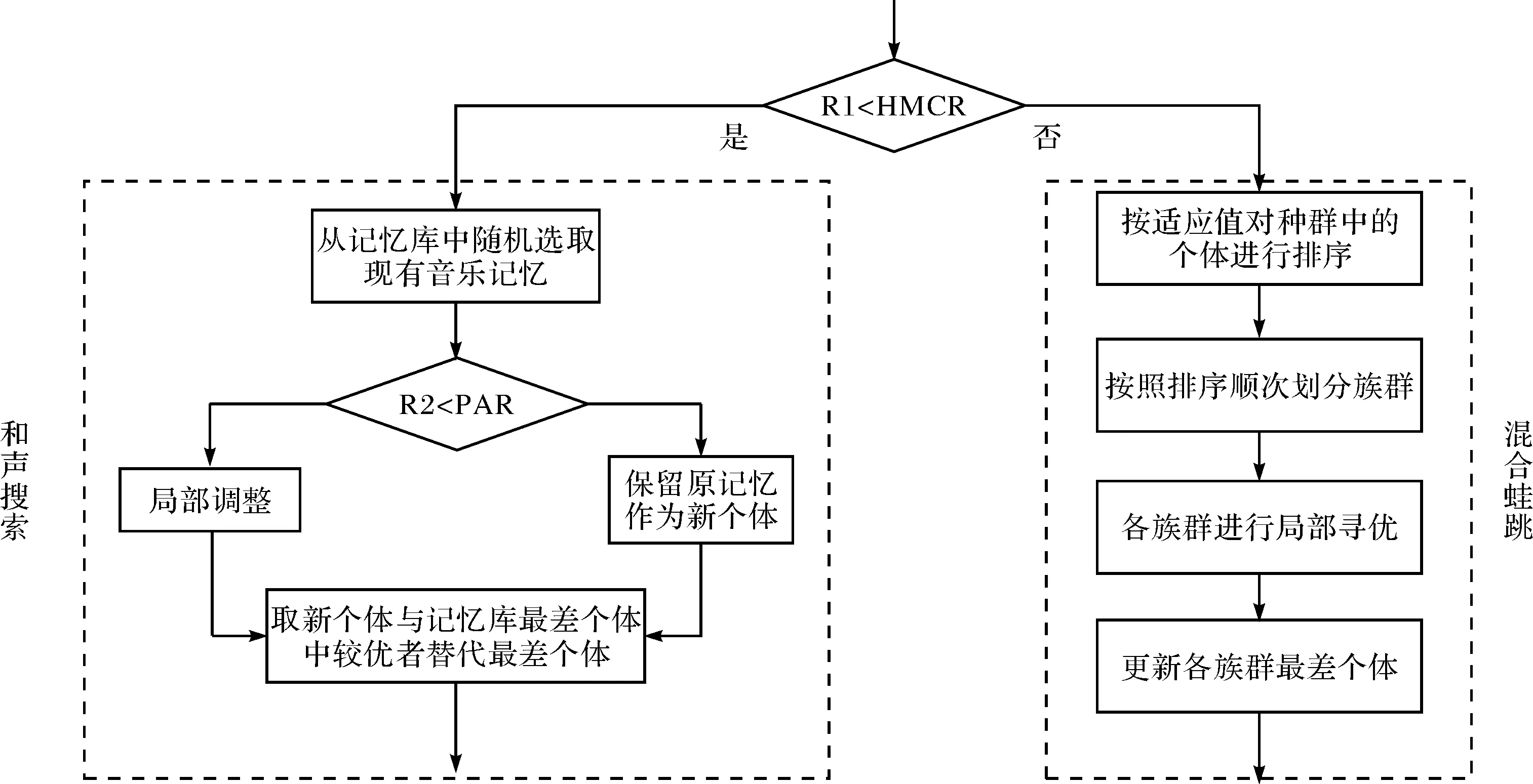
图1 互补搜索机制Fig.1 Complementary search mechanism
1.2.2自适应调整机制 上述互补搜索是基于记忆选择概率HMCR进行调整的.但是,固定的概率导致无法充分利用两种算法之间的互补性.为进一步促进随机搜索和导向性搜索之间的平衡,使算法在不同进化阶段有不同的搜索侧重,这里首先定义算法进化停滞系数ψ来衡量算法的进化能力,如式(6)所示.
ψ=n-1,
(6)
式中,n为种群最优个体的适应值连续不变的代数,即若连续n代最优个体的适应值f1=f2=…=fn,则种群停滞系数就等于n-1.
以算法停滞系数为参数对记忆选择概率HMCR进行动态控制,从而根据需要动态调用和声搜索和混合蛙跳两种算法.修改后的记忆选择概率HMCR计算方式如式(7)所示.
HMCR=HMCR0+ψ/50,
(7)
式中,HMCR0为初始记忆选择概率.
算法进化前期,算法停滞系数ψ为0或者较小,则HMCR相对较小,算法能以更大的概率进行混合蛙跳搜索.当算法出现进化困难趋于停滞时,算法停滞系数变大,则HMCR相对变大,算法能以较大概率进行和声搜索.即算法进化能力较强种群多样性较优时,通过调小HMCR促使算法侧重有导向性的寻优,更有利于种群个体向最优解收敛.当算法种群多样性变差进化能力下降时,通过调大HMCR促使算法侧重随机性搜索,更有利于拓展搜索空间,跳出局部最优.
1.3 和声蛙跳算法的实施步骤

Step2: ψ←ψ+1;
Step3: 按式(7)计算记忆选择概率HMCR;
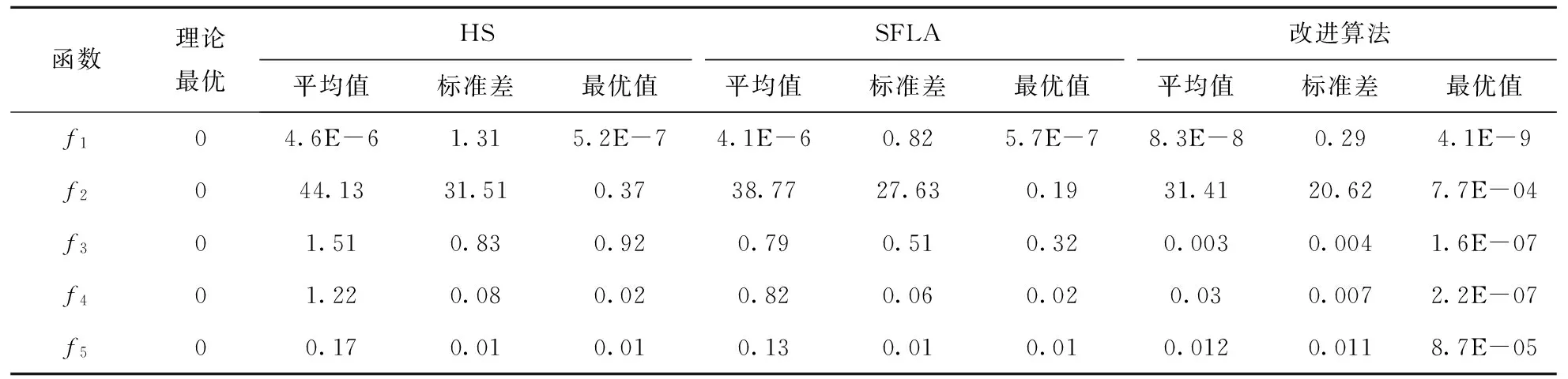
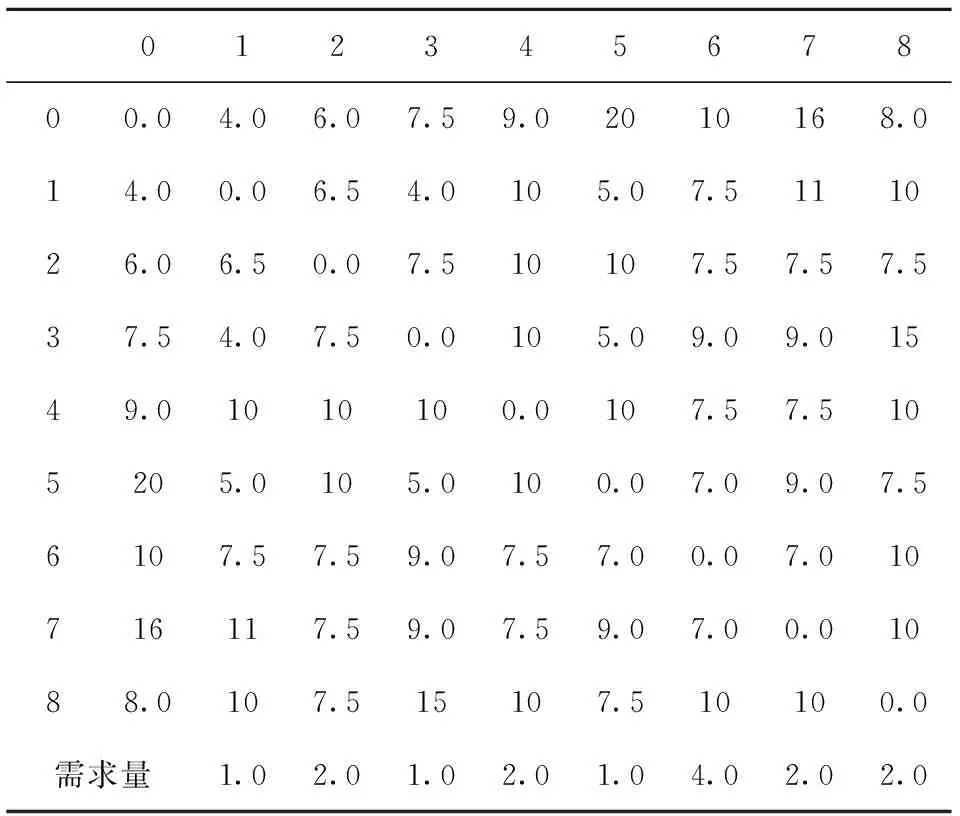
Step4: 动态调整算法进化的侧重,若rand() Step5: 循环次iter←iter+1; Step6: 判断算法是否达到最大迭代次数itermax,若达到,则算法停止,输出结果,否则继续执行Step7; Step7: 判断种群最优个体是否变化,若无变化,则返回Step2,若有变化,则令ψ=0并返回Step2. 和声蛙跳算法的框架如图2所示. 图2 和声蛙跳算法流程图Fig.2 Chart of harmony shuffled frog leaping algorithm 为验证本文提出的和声蛙跳算法的优化性能,将改进算法应分别用于标准测试函数的优化问题和车辆路径问题. 2.1 标准测试函数 本文采用式(8)~(12)等5个标准测试函数,如下所示: 1)Sphere函数: (8) 2)Rosenbrock函数: (9) 3)Rastrigrin函数: (10) 4)Griewank函数: (11) 5)Ackley函数: (12) 分别采用和声搜索算法、混合蛙跳算法、和声蛙跳算法对上述5个标准测试函数进行优化计算.算法参数设置如下:种群容量NP=200,族群个数m=5、初始记忆选择概率HMCR0=0.35、局部调整概率PAR=0.6、调整步长BW=0.01、最大循环次数itermax=1000; 采用上述3种算法对5个标准测试函数分别进行50次计算,取其平均结果进行对比,求解结果如表1所示. 表1 结果对比 对比表1中3种算法的优化结果可见,HS和SFLA两种算法的计算结果相差不大,改进后的算法无论是平均值还是最优值均优于前两种算法.对比不同算法优化结果的标准差可见,改进算法的优化结果浮动幅度小于HS和SFLA.由此可见,改进算法融合了HS和SFLA的优点,具有更强的全局优化能力,能够得到更优的优化结果. 2.2 车辆路径问题 车辆路径问题(Vehicle Routing Problem,VRP)是在满足车辆最大负载和客户需求的前提下,优化车辆的行驶路径使得运输成本最低、时间最短等目标得以实现.VRP问题的相关概念和数学模型可参考文献[7],本文在此不再赘述. 假定有8个分库和1个总库,总库有2辆车辆用于配送货物,每辆车的最大容量均为8t.要求合理安排车辆的配送路线,使得总的运输距离最短.各分库对总库的货物需求量以及各库之间的距离如表1所示(其中0表示总库). 表2 分库需求及各库之间距离 按2.1节相同的参数设置,分别采用HS、SFLA、改进算法对上述车辆路径问题进行20次优化,取各算法优化结果的平均值作对比,优化结果如表3所示. 表3 优化结果对比 对比3种算法求解上述VRP问题的计算结果可见,改进后的和声蛙跳算法的计算结果在多次求解的平均值、最优值和标准差3个方面均优于HS和SFLA.3种算法20次优化结果的分布如图3所示.结合表3中标准差的对比可知,和声蛙跳算法在求解车辆路径问题优化方面比HS和SFLA更具全局寻优能力,可以避免算法陷入局部最优解. 图3 优化结果分布情况Fig.3 Distribution of optimal results 本文针对和声搜索算法进化中随机生成新元素难以保证产生有效个体的问题,将混合蛙跳算法作为子模块嵌入和声搜索算法中,并以算法停滞系数为控制参数动态调整两种算法的侧重,从而将随机搜索与导向性搜索结合,达到全局搜素与局部寻优的平衡.将改进算法应用于标准测试函数和车辆路径问题的优化,模拟计算结果表明:本文提出的改进算法具有更强的全局搜索能力,得到的解更优,适合用于求解复杂优化问题. [1] ZONG W G, JOONG H K, LOGANATHAN G V. A new heuristic optimization algorithm: harmony search[J]. Simulation, 2001, 76(2):60-68. [2] LEE K S, GEEM Z W. A new structural optimization method based on the harmony search algorithm[J]. Computers & Structures, 2004, 82(9):781-798. [3] 高立群, 依玉峰, 郑 平. 和声搜索算法在求解最短路径问题中的应用[J].东北大学学报(自然科学版), 2011, 32(6):769-772. [4] 王 蕊, 夏 军, 张文华. 和声搜索算法在非线性马斯京根模型参数率定中的应用[J].水电能源科学, 2008, 26(4):36-39. [5] EUSUFF M M, LANSEY K E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J]. Journal of Water Resources Planning and Management, 2003, 129(3):210-225. [6] 李英海, 周建中, 杨俊杰. 一种基于阈值选择策略的改进混合蛙跳算法[J].计算机工程与应用, 2007, 43(35):19-21. [7] LENSTRA J K, RINNOOY K. Complexity of vehicle routing and scheduling problems[J]. Networks, 1981, 11(2):221-227. Harmony frog leaping algorithm and its application to complex optimization problems XIAO Wenxian, WANG Junge, MA Xiaoqin (Henan Institute of Science and Technology, Xinxiang, Henan 453003) When harmony search algorithm is used in solving complex optimization problems, it creates new elements via a random manner. This evolutionary strategy will affect the performance of the algorithm because the search process is difficult to ensure an effective individual. In response to these problems, shuffled frog leaping algorithm will be embedded in harmony search algorithm as a sub-part. The randomness of harmony search and the guidance of shuffled frog leaping algorithm are coupled. Adaptive factor is defined in this paper, and algorithms are invocated dynamically based on the factor so as to realize the coupling dynamic search. The improved algorithm is applied to the standard test functions and the optimization of VRP, the simulation results show that the improved algorithm has better global searching ability. Meanwhile it gets better solution and is suitable for solving complex optimization problems. optimization problems; harmony search algorithm; shuffled frog leaping algorithm; coupling search; dynamic balance 2015-03-02. 国家自然科学基金项目(71171151);河南省教育厅自然科学研究计划项目(13B520011). 1000-1190(2016)02-0211-05 TP301.6 A *E-mail: xwenx@yeah.net.
2 算例






3 结论
