基于锤击法的木工双摆角铣头模态分析

王双永

（中国林业科学研究院 木材工业研究所，北京 100091）

基于锤击法的木工双摆角铣头模态分析

王双永

（中国林业科学研究院 木材工业研究所，北京 100091）

根据多体系统理论与模态分析原理，综合考虑木工双摆角铣头的结构特点，确定采用试验模态分析方法，研究木工双摆角铣头的振动特性；提出运用PULSE多分析仪系统，采用锤击法对木工双摆角铣头整体结构进行试验测试分析；得出木工双摆角铣头前六阶模态对应的固有频率、阻尼比和结构模态振型，结果表明该木工双摆角铣头抗振性能满足木材加工要求。

木工双摆角铣头；试验模态；锤击法；振动特性

0　引言

木工双摆角铣头是木材高速加工中心的核心功能部件，其动力学性能直接影响加工精度，研究木工双摆角铣头的动力学特性对提高加工质量具有重要意义。通常采用模态分析法获得关键结构的固有频率和模态振型，结构的动刚度及抗振性能很大程度上取决于固有频率，薄弱结构可以通过模态振型反映出来。相比理论分析和虚拟模态，试验模态具有操作简单、分析结果可信度高等优点，应用越来越广泛[1,2]。本文主要采用试验模态分析方法，对木工双摆角铣头进行振动特性分析，得到相关结构动力学参数及可视化的整机模态振型，为进一步的结构改进与性能优化提供参考。

1　模态分析概述

模态分析主要包括虚拟模态和试验模态两种方法。虚拟模态是利用ANSYS、ADAMS等有限元分析软件进行一定的简化分析得到机械结构的理论固有频率与振型，主要用于单一零件或结构不太复杂的关键部件的动态分析。试验模态则是通过试验激振设备对机械结构进行激振，动态测量系统通过加速度传感器接收激励和振动响应信号，再通过模/数转换和快速傅里叶变换（FFT）处理相关数据，计算出各种函数，得出各阶固有频率、阻尼比和振型等参数，根据结果分析系统结构的动力特征，锤击法是模态试验中较简单的一种方法[3]。

锤击法是运用力锤敲打系统结构的被测点，力锤上的测力传感器拾取激励信号，拾振点的加速度传感器拾取响应信号，然后通过现代测试技术手段，借助脉冲实验原理、FFT和莫泰理论等，解出被测结构的传递函数，进而获得相应模态参数。这种方法快速、准确、简单、有效，能够反映出被测结构的振动属性。

对系统结构输入一个脉冲信号，被测结构将会产生微幅振动，即产生位移、速度和加速度等响应信号[4,5]。通过计算脉冲信号自功率谱响应信号自功率谱SXX(f)以及脉冲响应信号互功率谱SYX(f)，可获得结构频响函数H(f)和相干函数具体公式如下：

假设单位理想脉冲的持续时间为无穷小，则可用狄拉克函数表示为：

其傅里叶变换为：

2　铣头模态试验

2.1试验工具

本试验采用B&K公司的PULSE多分析仪系统，包括的工具型号及参数如表1所示。分析软件具有Model分析和FFT分析等功能，主要用于采集分析激励信号及加速度响应信号等。

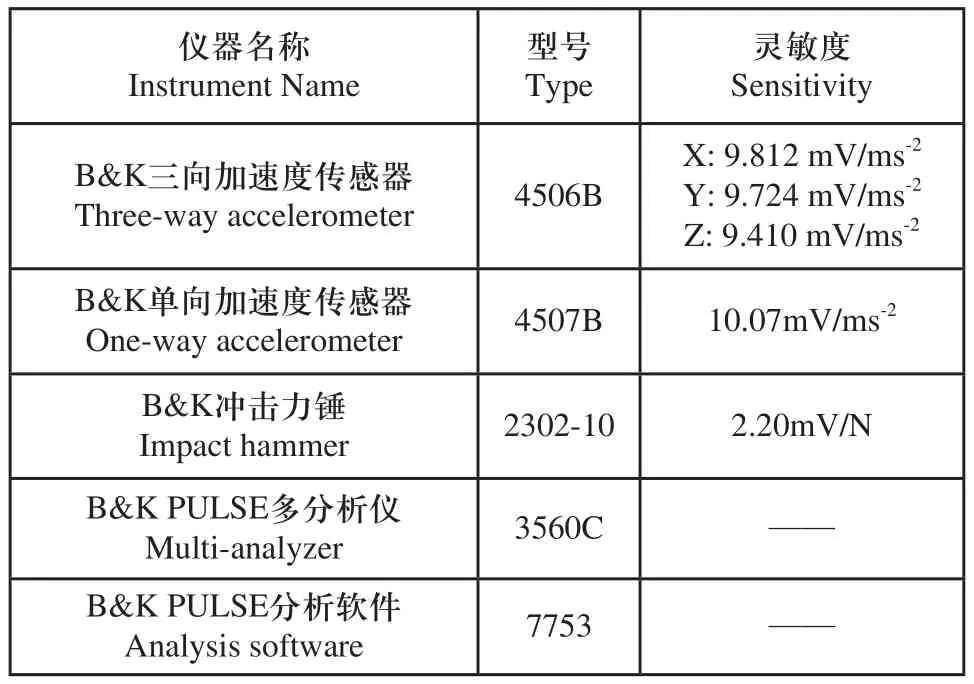
表1　试验工具型号及参数

测试对象为木工双摆角铣头，由PULSE多分析仪系统和被测木工双摆角铣头组成的试验平台如图1所示。

图1　模态试验平台

测试原理如图2所示。安装在冲击力锤前端的测力传感器通过锤击木工双摆角铣头的测点，产生激励信号，固定在木工双摆角铣头上的加速度传感器拾取加速度响应信号，所有信号通过数据采集分析仪的采集、滤波、放大等处理，传输给计算机，通过模态测试分析软件得出试验模态结果。

图2　模态测试原理

2.2试验过程

试验所测的木工双摆角铣头属于轻载型单臂悬挂式结构，主要包含两个摆轴及主壳体支撑，为模拟实际工况采用固定支撑方式[6]。为尽可能完整的获取模态信息，并遵循拾振简化的原则，结合该木工双摆角铣头的结构特点，设置31个拾振点，测点分布及相应编号如图3所示。

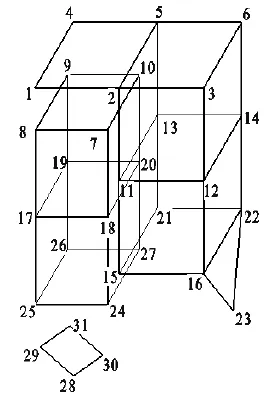
图3　测试点分布及编号

本试验采用固定响应参考点的方式，用蜂蜡将加速度传感器固定在高速电主轴前端外侧，符合右手笛卡尔坐标系。根据模态分析原理，结合木工双摆角铣头结构特点进行参数设置，每个拾振点重复试验5次。

通过多分析仪系统对冲击力和响应加速度数据进行采集，内部进行FFT变换处理及综合分析，然后由Measurement得出某一测点的加速度频响函数曲线和相干函数曲线，分别如图4和图5所示。

图4　某一测点加速度频响曲线

图5　某一测点相干函数曲线

由图4可知，该木工双摆角铣头的振动加速度频率响应曲线的波峰主要集中在0～200Hz范围内，最大峰值对应的频率在170Hz～190Hz之间。结合图5，该测点的相干函数曲线波动较小，基本上趋于稳定，表明该测点的振动加速度频率响应信号有效。

综合考虑实际加工工况和可能引起共振的频率范围，选择提取测试结果的前六阶模态进行分析。

2.3试验结果处理与分析

由于实际试验环境条件较为复杂，存在一定不可预知的干扰，实测曲线存在一些小波动，通过模态辨识对其拟合，消除不必要的干扰[7]。

将实际测得木工双摆角铣头结构频响函数曲线与软件拟合曲线进行对比，如图6所示，其中黑色曲线代表实测结果，红色曲线代表拟合结果。所得拟合曲线能够反映实测结果的变化趋势，由图可以看出前六阶固有频率相对比较集中，第七阶固有频率大于800Hz。

图6　结构频响函数曲线拟合结果比较

通过MEScope软件的模态振型分析功能，结合试验数据可得木工双摆角铣头整机结构各阶模态对应的模态振型，如图7所示。

图7　木工双摆角铣头模态振型

通过结构模态辨识的参数计算，可得木工双摆角铣头各阶模态对应的固有频率和阻尼比，表2为整机结构的模态参数及相应的振型描述。

2.4试验结论

通过以上试验模态结果分析，木工双摆角铣头前六阶模态对应的固有频率在30Hz～200Hz范围内，阻尼比2%～9%，该结构可以有效避免共振。由结构模态振型结果分析可知，该木工双摆角铣头整体结构绕Z轴扭转的振型形态最为显著，因此，要重点优化木工双摆角铣头主壳体支撑结构，以提高该结构绕Z轴的扭转刚度。

【】【】

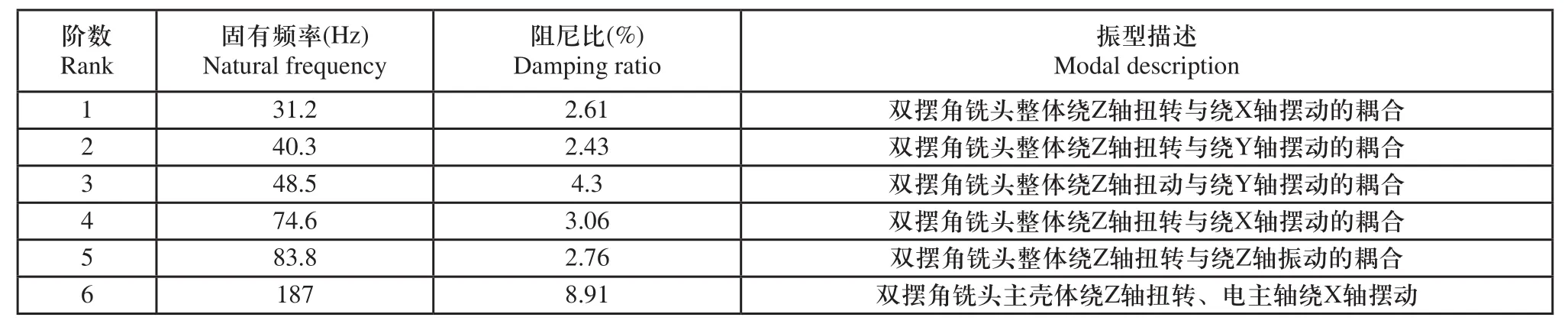
表2　结构模态参数及振型描述

第一阶（31.2Hz）和第四阶（74.6Hz）模态时的振型，主要是木工双摆角铣头结构整体绕Z轴扭转和绕X轴摆动的耦合，即工作过程中对A轴位置精度的影响较大，对C轴位置精度的影响较小；因此，在A轴驱动工作时，应尽量避免第一阶和第四阶固有频率。

第二阶（40.3Hz）和第三阶（48.5Hz）模态时的振型，主要是木工双摆角铣头结构整体绕Z轴扭转和绕Y轴摆动的耦合，即工作过程中对C轴和A轴位置精度的影响均较大；因此，只要所有工作状态下都应尽量避免第二阶和第三阶固有频率。

第五阶（83.8Hz）和第六阶（187Hz）模态时的振型，包括木工双摆角铣头结构整体绕Z轴扭转和绕Z轴振动的耦合、主壳体支撑绕Z轴扭转和电主轴绕X轴摆动，主要影响对C轴传动位置精度，而且在第六阶模态时出现电主轴绕X轴摆动的趋势；因此，应提高木工双摆角铣头部件的装配精度及可靠性，保证高速电主轴的装配刚度。

总体来说，该木工双摆角铣头的阻尼比相对较大，可以有效减小整体结构的共振振幅，共振频率相对集中，可以有效避开该范围。另外，木工双摆角铣头的主轴工作转速范围18000～24000r/min，其自激振动频率远大于以上六阶固有频率，且远小于第七阶固有频率。因此，如果不考虑摆轴驱动电机和实际切削异常产生振动的影响，该木工双摆角铣头工作时不会发生共振现象。

3　结束语

综合考虑木工双摆角铣头的结构特点，提出运用PULSE多分析仪系统，采用锤击法对木工双摆角铣头整体结构进行试验模态分析。根据锤击法和振动测试原理，介绍了试验步骤及注意事项，通过试验得出木工双摆角铣头前六阶模态对应的固有频率、阻尼比和结构模态振型，最后对试验结果进行了分析，结果表明该木工双摆角铣头抗振性能满足木材加工要求。本文采用的试验原理与分析方法可为木工双摆角铣头及木材高速加工装备的结构改进与性能优化提供参考依据，对完善木材高速精深加工、提高木材加工质量和利用率、节能环保等具有重要意义。

[1] Wang SY, Zhang W, Zhang QW, et al. Reliability Analysis about A/C-axis of Woodworking Five-axis Milling Head[J].Applied Mechanics and Materials.2014:407-410.

[2] 蔡力钢,马仕明,赵永胜,等.重载摆角铣头模态分析与实验研究[J].振动与冲击, 2011(7):250-255.

[3] 傅志方,华宏星.模态分析理论与应用[M].上海:上海交通大学出版社,2000.

[4] 陈艳,张松,赵滨,等.高速龙门加工中心摆角铣头动态特性分析[J].制造技术与机床, 2014(7):68-73.

[5] 黄礼彬,赵波.试验模态分析中的锤击法[J].洛阳工程院学报, 1990,11(2):35-42.

[6] 王双永,张伟,张鹏飞.木工双摆角铣头C轴回转精度测试与分析[J].制造技术与机床,2015(6):139-142.

[7] 陈甜甜.龙门铣床双摆头动力学特性实验研究[J].机床与液压, 2013(19):7-11.

Modal analysis of woodworking swing milling head based on hammering method

WANG Shuang-yong

TH161

A

1009-0134(2016)02-0089-04

2015-10-13

王双永（1988 -），男，山东滕州人，研究实习员，硕士，主要从事木材加工及检测技术装备研究与开发工作。